一道热学题“一题多解”的深度剖析及启示

刘大明 江秀梅

(江西省抚州市第一中学 344000)

一、提出问题

一题多解是物理试题解答中常见的现象，其特征是“殊途同归”；但是，“殊途不同归”的“一题多解”现象很少见.下面这道热学试题，有三种解法，且所得结果相差巨大，最为关键的是，一线教师一时还难以判断孰是孰非.试题呈现如下：

图1

题目一个横截面积S=20 cm2，内壁光滑且导热良好的气缸直立放置，如图1所示，质量m=2 kg的活塞下方封闭了一定量的理想气体，稳定时，气柱长度h=20 cm，现把一个质量为M的物块放置于活塞上方，待系统稳定后，被封闭气柱长度h′=10cm，已知外界大气压p0=1×105Pa，重力加速度g=10 m/s2，外界温度不发生变化.求：

(1)物块的质量M；

(2)该过程中气体与外界发生热交换的情况.

解析(1)初态对活塞由平衡条件得

p0S+mg=p1S(1)

放上物块待稳定后有

p1Sh=p2Sh′ (2)

此时对活塞由平衡条件得

p0S+mg+Mg=p2S(3)

联立以上三式代入数据可得

M=22kg.

(2)解法1 整体考虑能量守恒，活塞及其上物块减少的重力势能通过气体热交换耗散于外界环境中(转化为外界内能)，所以Q=(mg+Mg)(h-h′)，代入数据得到Q=24J.

解法2 对活塞全过程使用动能定理：(Mg+mg+p0)(h-h′)-Q=0-0，其中封闭气体对活塞做负功，数值等于热交换耗散于外界环境的热量Q，代入数据计算得到Q=44 J.

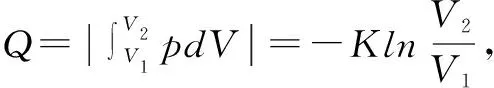
第(1)问没有异议，故不讨论.本文就第(2)问进行探讨：乍一看起来，3种解法都没有明显的错误，实际上，不同教辅书籍确有不一致解答，不同教师也可能给出不一致的解答.那么，3种解法，孰对孰错？问题何在，如何破解？

就这道题，笔者所在单位也进行了热烈讨论，起初也想法不一，观点迥异.下面就讨论过程加以描述，并进行抽丝剥茧，一一剖析.

二、问诊把脉——解法剖析

1.对解法1的剖析

解法1 的思考基础是能量转化，认为：全过程只有活塞上物体的重力势能减小，活塞上方大气重力势能忽略不计，又因温度不变，封闭气体内能不变，因此，重力势能减少是通过封闭气体热交换耗散于环境中，转化为外界内能.其中，大气对活塞做功对应什么能量转化，因为平时接触较少，极容易忽视，而且，“常识”让我们想当然地认为，大气的状态并不会因活塞移动发生“显著”变化，因而大气重力势能“不变”，于是，大气对活塞做功一并忽略了.大气对活塞做功肯定不可忽略，然而其对应的能量转化关系是怎样的？下文将构建等效模型给予说明.

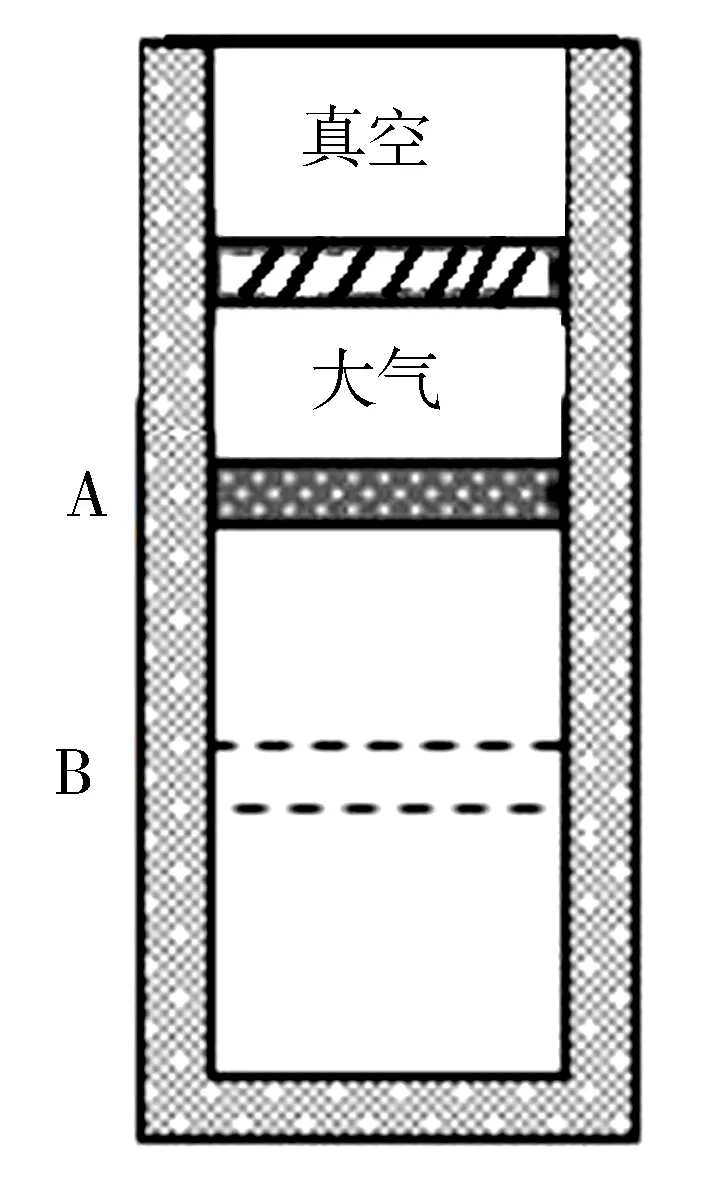
图2

2.对解法2的剖析

解法2的思考基础是动能定理.活塞首末状态明确(静止)，而且活塞受到各个力的做功情况也清楚，运用动能定理求封闭气体对活塞这一变力作功，也是不难想到的.对解法2，难以给出具有说服力的反驳理由，但要坚持本解法，无疑要回应解法1的问题关切.可以构建如图2所示等价模型加以辨析.

设大气压强为p0，其上方活塞重力满足m′g=p0S.当A处活塞放上物块M后，封闭气体的状态变化跟题目情景一致.显然，大气和其上活塞会一起下降10cm.大气对其上方活塞做负功、对其下方活塞做正功，且数值相等，从而实现了上方活塞重力势能转移(化)到封闭气体里，当然最终通过热交换耗散于环境中.这个等价模型很好地说明了，大气做功不可忽略，其对应的正是重力势能的变化.因此，这个等价模型印证了解法2，否定了解法1.

3.对解法3的剖析

解法3中，把全过程理解为满足理想气体状态方程的等温变化，是一个误解！也即，前提条件pV=K(常量)在全过程中不成立，从而解法3不正确.

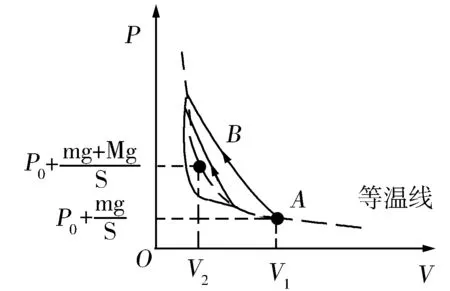
图3

至此，似乎可以下结论：解法2正确.然而，在交流讨论中，就解法2，一位同事提出了一个挑战性疑点.

4.针对解法2的挑战性疑点

众所周知，在导热良好条件下，封闭理想气体缓慢压缩过程为等温变化过程，也是准静态过程，如图3的虚线反比例曲线所示，反比例曲线段AB与V轴所围面积大小表示封闭气体对外界所做的功，也正是解法3计算的热交换对应的能量.值得强调，“缓慢”条件的重要性，宏观上看，压缩所需的外力是一个渐变变力；微观上看，封闭气体分子与活塞碰撞前后速率不变.然而，题目情景所加外力是一个恒力，活塞运动不可能“缓慢”，而是围绕B所对应平衡位置(对封闭气体而言，也是一个平衡态)做阻尼振动.从微观上看，活塞向下压缩时，由于活塞具有向下的速度，根据碰撞原理，封闭气体分子与活塞碰后速率大于碰前速率，封闭气体温度略微增加；相反，活塞向上回弹时，由于活塞具有向上的速度，所以气体分子碰后速率小于碰前速率，封闭气体速率略微减小.因此，封闭气体的p-V关系应是图3带箭头的实线所示.由此不难推断：在压缩过程，封闭气体克服外界做功大于等温变化过程；相反，在膨胀过程，封闭气体对外界做功小于等温变化过程，这个反差很好地说明了：在全过程，封闭气体克服外界做功大于等温变化过程.从图像上定性来看，这些反差累加结果很可能等于44 J-30.5 J=13.5 J，从而否定了解法3，印证了解法2，如此，挑战性疑点得到破解.

三、拓展与启示

在教育教学中遇到一些难题是常有的事；就这些难题进行交流讨论，也十分必要.毋庸置疑，对这些难题进行深入分析，是促进教师专业成长的必经之路；对这些难题进行交流探讨，是教师间进行专业研讨的重要形式.然而，结合上面教学案例，就某些误区提出一些看法和建议：

1.站高点才能领略“一览众山小”

不少教师认为，中学教师在大学所学的专业知识就中学教学没有多大作用.特别是，“(师范)学得好，(入职)教不好”的反差现象，成为这一观点的佐证.在应试环境下，考试成绩成为了教学业绩的唯一衡量标准.然而，考试成绩好与坏，取决于众多因素，而且可以通过各种途径实现，题海战术、拼时间几乎是实现考试成绩好的普遍做法.一般地，在应试泛滥的学校，诸如前文教学案例呈现的专业研讨就非常少见；同样，持有错误观念的教师，面对一些教学难题时也难以深入研究，于是只能要求学生死记答案.笔者未重新翻阅大学教材之前，根据导热良好条件守定为等温变化，从而坚持解法3正确；待翻阅大学教材后，温故“准静态过程”后，就明白了自己之前的固执观点的问题所在.中学教师应该时常翻阅大学教材；遇到教学难题，温故大学教材一般能寻找到解决之道.教师站高点，才能发现教学过程中存在的前概念、迷思概念，否则面对自己的前概念、迷思概念，就难以自我突破.

2.不经教研谈不上专业成长

很多学校已经不重视教研，有教学无教研现象非常普遍.邢红军教授认为，论文写作是最佳的教研历练方式，也是实现教师专业成长必经之路.然而，由于种种原因，论文写作不再是衡量教学水平的重要标志了，这将会是中学教学中的一个灾难！在前述教学案例中，没有一定教研水平的教师，难以构建等效模型来阐述问题，也难以深入微观视角破解挑战性疑点.事实上，钱伟长院士就提出“无教研无教学”的教学观点.

3.专业讨论中践行人格平等理念

物理试题中出现殊途同归的一题多解现象非常普遍，在教学研讨中，就某道题“你一法我一策他一计”式的热烈研讨，尤为津津乐道！教学论文中多半呈现这样的教学案例.从心理学角度而言，这是最安全的讨论，讨论在一片点赞中愉快进行.相反，诸如前述殊途不同归的“一题多解”的教学研讨中，极容易冷场，原因在于某些想法或观点被“证伪”时，“一喜一忧”总让人尴尬.所以，推进专业讨论，务必构建人格平等观念，避免能力方面的评判，如此才能在彼此“失误”中汲取营养实现共同成长.在前述案例研讨中，正确解法的确立是建立在各种错误解法的证伪上实现的，聚焦了所有研讨教师的智慧.