碳钢塑性变形对增量磁导率信号的影响

李丽娟 解社娟 陈洪恩 陈玲莉 何曼如 陈振茂

1.西安交通大学机械结构强度与振动国家重点实验室，西安，710049 2.西安交通大学陕西省无损检测与结构完整性评价工程技术研究中心，西安，710049 3.中国核动力研究设计院核反应堆系统设计技术国家重点实验室，成都，610041

0 引言

核电结构材料的塑性变形严重影响核电安全和核电设备的使用寿命。日本福岛核电站堆芯熔毁事故凸显了核电结构安全的重要性。除全电源丧失可能导致堆芯无法冷却而引发堆芯事故外，冷却所必需的大量核级管道的塑性变形、局部减薄等缺陷的发生和发展也可能导致核级管道的泄漏甚至大破裂，对核能结构安全造成严重威胁。因此，对出现宏观缺陷之前的塑性变形进行无损评估，定期进行定量无损检测以保障设备的安全性和经济性是非常必要的［1⁃3］。目前对塑性变形、应力及残余应力的检测手段主要有：增量磁导率法、Barkhousen 法［4］、金属磁记忆检测［5⁃8］、脉冲涡流法［9⁃11］、非线性超声检测［12］、X 射线衍射法［13］，但对微观缺陷（如塑性变形、疲劳、蠕变和材料劣化）的检测和定量评价仍然亟待进一步研究。在这些目前已有的微观缺陷无损检测方法中，射线方法对人体危害较大，超声方法需要耦合剂，而增量磁导率法有望实现对塑性变形的定量无损评价。

德国研究机构IZFP的DOBMANN等［4］最早基于实验方法提出了增量磁导率（magnetic incre⁃mental permeability，MIP）法对评价塑性变形的可行性，之后一些学者分别建立了增量磁导率数值模 拟 方 法［6，14⁃20］。 YANSHAN 等［14］采 用 基 于Cheng、Dodd和Deed算法求解的增量磁导率半解析模型，将具有塑性变形的试件简化为多层介质（每层介质的厚度及电磁特性已知）。值得注意的是，对于无损检测而言，通常难以得知具有塑性变形结构每层介质的厚度及电磁特性参数。GABI等［15］同样地将具有塑性变形的试件等效为多层板模型，采用Jiles-Atherton模型（JA模型）描述不同饱和磁场的B-H曲线，使用FEM Flux软件进行数值模拟。值得注意的是，JA模型并不精确，且由JA模型描述的B-H曲线并不是一个中心对称的闭合曲线。而D’AQUINO等［18⁃19］采用了JA模型的各向同性矢量推广的方法引出向量磁滞回线模型（M-H曲线），并用Galerkin方法和棱边元有限元法在时间域求解，给出了三个方向分量的增量磁导率信号曲线，其主要工作为建立增量磁导率信号的三维线性及非线性数值模拟方法。陈洪恩等［6，16⁃17］采用 Ar法和 FEM-BEM 法（边界元有限元法）对一个具有磁导率分布的铁磁性平板试件进行了增量磁导率信号的数值计算，但其数值计算结果中增量磁导率信号曲线的平滑性与实验结果对比较差。

BOLLER等［21］在报告中指出，增量磁导率的峰值对应力的影响较为敏感。GRIMBERG等［22］设计了一个应用增量磁导率进行无损检测的系统，并发现用增量磁导率法测定的矫顽力随疲劳次数的增大而增大。RYU等［23］针对汽轮机中的1Cr-1Mo-0.25V材料长期受高温环境的影响，研究了应用可逆磁导率法来评估材料寿命的方法，研究发现可逆磁导率峰峰距（PIRMP）随着材料使用寿命的延长而下降，由此可以用可逆磁导率法来评估材料的使用寿命。但铁磁材料的塑性变形对增量磁导率信号的影响机理尚不明确。

基于以上背景，本研究从数值模拟角度，将B-H曲线的特征量导入数值计算中，间接分析塑性变形对增量磁导率信号曲线的影响规律，研究了塑性变形对增量磁导率信号的影响机理。

1 增量磁导率测量方法

1.1 增量磁导率定义

增量磁导率μΔ的定义为μΔ= ΔB/(μ0ΔH)，其中，ΔB为磁通密度，磁场强度ΔH应该足够小以确保不会发生布洛赫磁壁跳跃，且ΔH随时间正弦变化，μ0为真空磁导率，μ0=4π× 10-7H/m。

根据以上定义，增量磁导率可以通过图1所示的系统测得。图1中，电磁铁由绕在U形磁轭上的磁化线圈和磁轭构成，其磁化线圈中通有低频高幅值正弦激励电流。电磁铁用于产生外加强磁场以使得被测铁磁性材料试件处于磁滞回线中的不同磁化状态。放置于被测铁磁性材料试件上方的两个线圈构成涡流探头，其中涡流激励线圈位于上方，涡流检出线圈位于下方。涡流激励线圈中通入高频正弦电流，使其产生一个幅值较小且频率较高的正弦变化的磁场，附加在电磁铁产生的低频强外加磁场上。若用图2表示，即电磁铁产生的低频强正弦磁场可表示为图2中的大环（磁滞回线），激励线圈产生的高频弱正弦磁场可表示为图2中可逆的小环（可逆磁导率）。

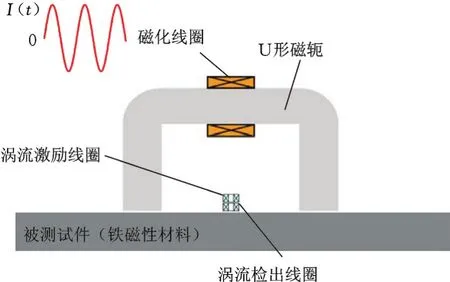
图1 增量磁导率测量系统示意图Fig.1 Schematic of MIP method

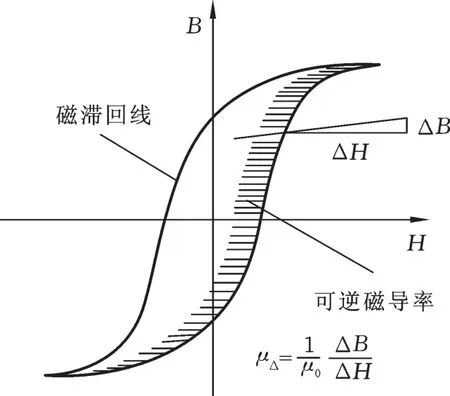
图2 增量磁导率定义和非线性B-H曲线［14］Fig.2 MIP and the nonlinear B-H curve［14］

作为初步研究，假设外加强磁场使被测铁磁性材料试件产生的磁化是均匀的。由于电磁铁的磁化线圈中通入的磁化电流一般为低频电流，例如典型频率通常为1 Hz，而涡流激励探头中通入的激励电流信号的频率通常为kHz量级，二者频率大小相差较大，因此可以不考虑低频外加强磁场在被测试件中产生的涡流效应，即，可以将电磁铁产生的正弦变化的连续场离散为许多个准静态场，并由此将图1所示问题简化为单纯的外加准静态强磁场下的简单涡流问题。其中外加准静态强磁场的影响可等效为涡流问题中被测铁磁性试件磁导率的变化。

检出线圈的电压信号与增量磁导率信号的比例关系根据文献［14］可知：当采用自激自检线圈时，该线圈检出信号为阻抗信号；根据电磁感应定律可知，对于时谐问题，检出线圈感生电压ΔU=-jωΔBS，即线圈两端电压ΔU与通过该线圈的磁通密度ΔB成正比，S为导线环路面积；而根据麦克斯韦全电流定律，线圈内的磁场强度ΔH与通过线圈的电流Δi成正比；因此，根据增量磁导率的定义，μΔ= ΔB/(μ0ΔH)，即有，μΔ正比于ΔU/Δi。对于本文研究中所使用的激励-检出线圈，其检出线圈的检出信号为电压信号，而对于时谐问题线圈中通入的正弦电流Δi的幅值不变，因此μΔ正比于ΔU的关系成立，即检出线圈的电压信号与增量磁导率信号为比例关系。

由于涡流问题中检出线圈的电压信号与增量磁导率信号为比例关系，可以将外加准静态磁场的磁场强度H作为横轴，涡流检出线圈的电压信号作为纵轴，即可等效模拟增量磁导率信号曲线。通过使外加准静态磁场遍历一个铁磁性材料的磁滞特性曲线，即遍历电磁铁激励信号的一个完整周期，可以逐点得到增量磁导率信号，并构成整个周期上的封闭的增量磁导率信号曲线。

塑性变形会使晶体内产生点缺陷、位错等微观缺陷，这些微观缺陷会影响材料的电磁特性，因此通过考察材料的电磁响应参数（如增量磁导率信号）可以间接表征材料的塑性变形。基于此，通过求解图1所示的问题，可得到增量磁导率信号曲线并描述试件的塑性变形状态。

1.2 增量磁导率法数值计算原理

假设U形电磁铁在所研究区域内产生的场是均匀场，即，假设在所研究区域内被测试件的磁化是均匀的。由于前面已经将U形电磁铁的1 Hz正弦激励信号产生的场假设为该周期内每个时间离散点上的准静态场，可将电磁铁产生的场的作用等效为每一时间离散点上被测试件磁导率的变化。因此图1所示的增量磁导率问题可以简化为不同磁导率的被测试件的涡流检测问题。其中，被测试件的磁导率由电磁铁产生的准静态场及被测试件的B-H曲线确定。由于电磁铁产生的场为强磁场，故试件的非线性B-H特性可以用下式描述：

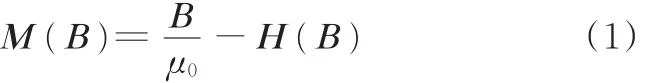
式（1）所描述的试件的非线性B-H曲线在本研究中由实验测量得到。在数值计算中，通过在每一电磁铁激励的时间离散点上对被测试件磁导率进行更新，并求解更新磁导率后的被测试件的涡流问题，即可得到该电磁铁激励的时间离散点上的增量磁导率信号。对电磁铁激励的一个完整周期上的所有离散点进行遍历计算，即可得到一个封闭的增量磁导率信号曲线。其中，对于涡流问题可基于退化磁矢位法计算，并得到当前时间步下的磁矢位A和检出线圈的电压信号。控制方程如下：

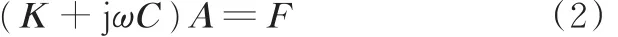
其中，K、C为方程的系数矩阵；F与激励有关。

本研究根据文献［24］建立的基于退化磁矢位法的涡流问题数值解法，开发了增量磁导率数值模拟程序，将电磁铁连续激励假设为该正弦激励周期内每个离散时间点上的准静态场，并将电磁铁的作用等效为每一离散点上被测试件磁导率的变化。在每一个电磁铁激励的离散点上，对试件的磁导率进行更新并求解涡流问题，得到当前时间点的涡流检出线圈的电压信号。通过计算一个完整周期的所有电磁铁激励离散点上的检出线圈电压信号，得到增量磁导率信号曲线。

2 结果与讨论

由于数值计算中无法直接引入塑性变形量，同时，考虑到铁磁性材料的塑性变形会使铁磁性材料的磁滞回线发生变化［4］，即：铁磁性材料的塑性变形会同时影响材料的剩磁和矫顽力；根据X射线实验数据，位错密度与残余塑性变形成正比例关系；随着位错密度的增大，残余应力在材料内部产生位错的钉扎效应使矫顽力增大；而随着位错密度的增大，剩磁减小［25⁃26］，因此，为研究增量磁导率信号曲线与塑性变形的关系，本研究将塑性变形量的变化等效为磁滞回线中磁特征量剩磁Br和矫顽力Hc的变化，并分别计算这些参数变化对增量磁导率信号曲线的影响，探讨其影响规律。作为初步研究，本研究考虑了剩磁和矫顽力单独改变的情况，即选取剩磁、矫顽力分别增大0、1%、2%、3%、5%，涡流探头的激励频率定为10 kHz，对上述每个工况进行计算，可得到对应的增量磁导率信号曲线。

本研究中的涡流探头为涡流检测线圈，涡流信号一般分为实部和虚部两部分，故数值计算得到的增量磁导率信号曲线也有两部分。涡流信号的实部反映了检出线圈的电压信号与激励信号相位相同的分量，虚部反映了检出线圈的电压信号与激励信号相位相差90°的分量。由于实部与虚部信号的规律基本一致，在本文中只给出了实部信号的结果，以下均只针对实部信号进行讨论分析。

图3给出了材料的B-H曲线与增量磁导率信号曲线的对应关系。由于材料的B-H曲线为中心对称结构，相应地，增量磁导率信号曲线也为对称结构。根据剩磁的定义，图3a中的剩磁点Br对应图3b中的A点（即磁场H=0的点）。而根据矫顽力的定义,图3a中的矫顽力点Hc对应图3b中的B点（即增量磁导率信号的峰值点B）。为了进一步讨论材料的B-H曲线中剩磁和矫顽力参数对增量磁导率曲线的影响规律，可参考图3 B-H曲线与增量磁导率曲线的每一部分的对应关系对数值计算结果进行分析，图3a中所标记的①～④部分分别对应图3b中的①～④部分。

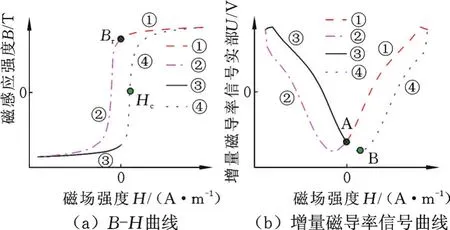
图3 B-H曲线与增量磁导率信号曲线的对应关系Fig.3 Correspondence between B-H curve and MIP signal curve

为了单独研究矫顽力和剩磁对增量磁导率信号曲线的影响，本文给出了分别计算矫顽力增加时剩磁保持不变，以及剩磁增加时矫顽力保持不变的增量磁导率信号曲线的结果，并对其进行了讨论。

2.1 矫顽力对增量磁导率的影响

图4为矫顽力单独增大时导入增量磁导率信号数值模拟计算程序中的B-H曲线。其中，矫顽力增值为0的B-H曲线为实验测得的碳素钢Q195的B-H曲线，矫顽力增大1%～5%时的B-H曲线由上述实验测得的曲线在H方向同比增大1%～5%得到，该方法保证了在矫顽力变化时另一个影响因素维持不变。当矫顽力变化时，将这5条B-H曲线导入计算中即可得到增量磁导率信号的数值模拟结果。图5所示为矫顽力增大0、1%、2%、3%、5%时数值模拟计算得到的实部信号，其中横轴为由电磁铁产生的外加准静态磁场强度H，纵轴为涡流检出线圈的电压信号的实部，该电压信号与增量磁导率信号成比例关系，因此可用电压信号来替代增量磁导率信号。

图4 不同ΔHc下的B-H曲线Fig.4 B-H curves under differentΔHc

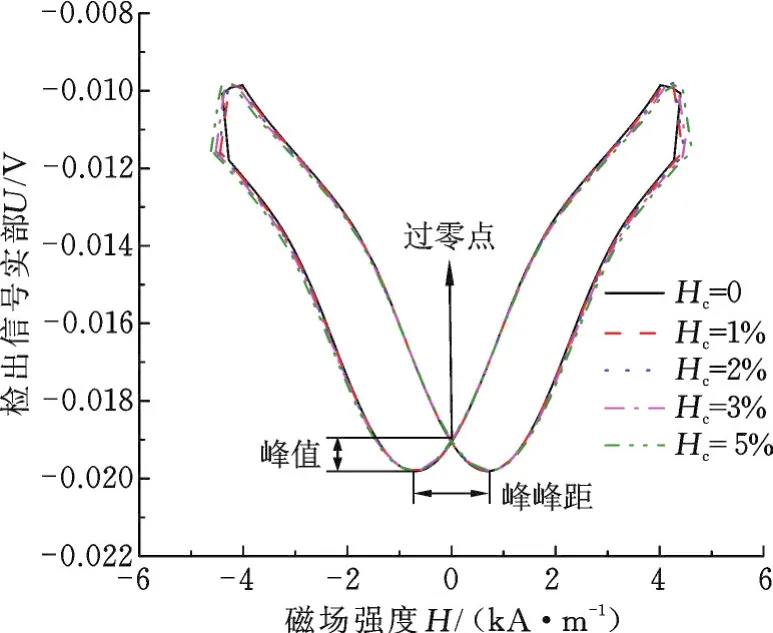
图5 不同ΔHc下的检出信号曲线Fig.5 Voltage signal curves under differentΔHc

为了更具体地分析增量磁导率信号的变化规律，从增量磁导率信号曲线（实部信号）中提取了峰峰距、峰值和过零点的绝对值3个典型特征量，并绘制了当矫顽力单独变化时这些特征量的变化曲线，见图5。

图6a表明，当矫顽力增大时，增量磁导率信号曲线的峰峰距增大。该结论中矫顽力与MIP信号曲线的峰峰距之间的强相关性与矫顽力的性质相符。根据图3所示的B-H曲线与MIP信号曲线的对应关系可知，MIP信号曲线的峰峰距的增大意味着B-H曲线上磁感应强度B=0时的外加磁场强度增大。图6b表明，当矫顽力增大时，增量磁导率信号曲线的过零点的绝对值减小，根据图3所示的BH曲线与MIP信号曲线的对应关系可知，MIP信号曲线过零点的绝对值对应B-H曲线上H=0的点处曲线斜率的绝对值，此时B-H曲线上H=0的点处曲线斜率的绝对值减小。图6c表明，当矫顽力增大时，增量磁导率信号曲线的峰值增大，根据图3所示的B-H曲线与MIP信号曲线的对应关系可知，MIP信号曲线的峰值对应B-H曲线上斜率最大的点，而B-H曲线上B=0处曲线斜率最大，此时BH曲线上B=0的点处曲线斜率增大。

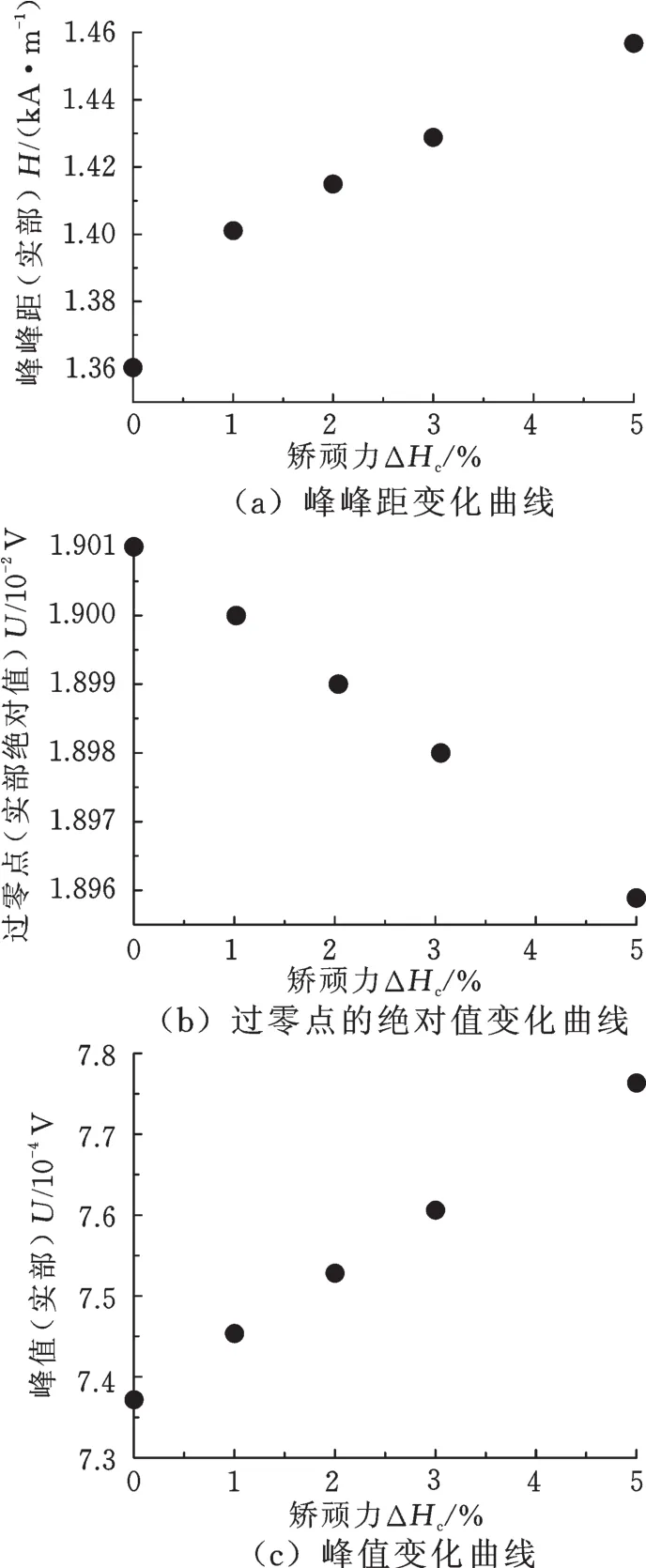
图6 矫顽力变化时增量磁导率信号曲线的峰峰距、过零点和峰值的变化规律Fig.6 Peak separation，zero crossing and peak value of MIP signal curves with differentΔHc

2.2 剩磁对增量磁导率的影响

同样地，图7为剩磁单独增大时导入计算中的B-H曲线，其中，剩磁增值为0的B-H曲线为实验测得的碳素钢Q195的B-H曲线，剩磁增大1%～5%时的B-H曲线由上述实验测得的曲线在B方向同比增大1%～5%得到，该方法保证了在剩磁变化时另一个影响因素维持不变。当剩磁变化时，将这5条B-H曲线导入计算中即可得到增量磁导率信号的数值模拟结果。图8所示为剩磁增大0、1%、2%、3%、5%时数值模拟计算得到的实部信号。

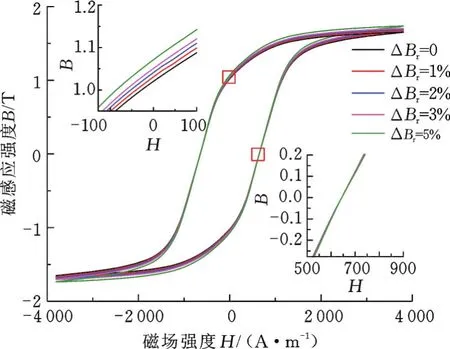
图7 不同ΔBr下的B-H曲线Fig.7 B-H curves under differentΔBr

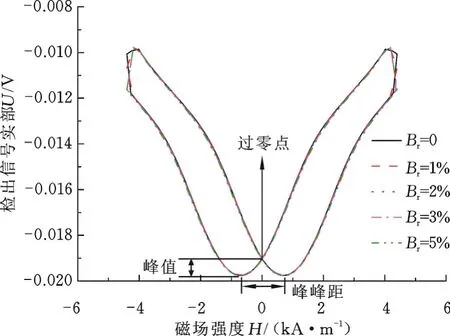
图8 不同ΔBr下的检出信号曲线Fig.8 Voltage signal curves under differentΔBr

为了更具体地分析增量磁导率的变化规律，提取峰峰距、峰值和过零点3个典型特征量，并绘制了当剩磁单独变化时这些特征量的变化曲线，见图9。

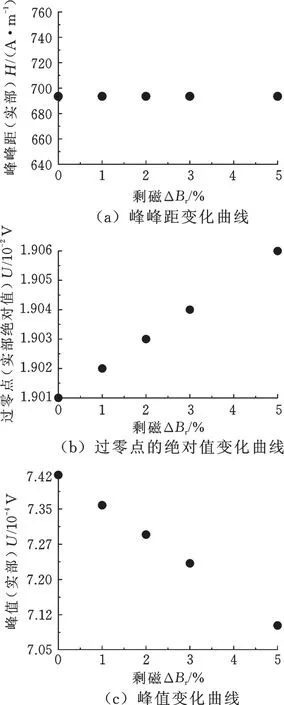
图9 剩磁变化时增量磁导率信号曲线的峰峰距、过零点和峰值的变化规律Fig.9 Peak separation，zero crossing and peak value of MIP signal curves with differentΔBr

图9 a表明，当剩磁增大时，增量磁导率信号曲线的峰峰距不变，剩磁的变化与增量磁导率信号曲线的峰峰距相关性不强。该结论中剩磁与MIP信号曲线的峰峰距之间的弱相关性与剩磁的性质相符。图9b表明，当剩磁增大时，增量磁导率信号曲线的过零点的绝对值增大，根据图3所示的B-H曲线与MIP信号曲线的对应关系可知，MIP信号曲线过零点的绝对值对应B-H曲线上H=0的点处曲线斜率的绝对值，此时B-H曲线上H=0的点处曲线斜率的绝对值增大。图9c表明，当剩磁增大时，增量磁导率信号曲线的峰值减小，根据图3所示的B-H曲线与MIP信号曲线的对应关系可知，MIP信号曲线的峰值对应B-H曲线上斜率最大的点，而B-H曲线上B=0处曲线斜率最大，此时B-H曲线上B=0的点处曲线斜率减小。塑性变形时，随着位错密度的增大，剩磁减小。

本文所述研究采用增加剩磁的途径分析剩磁的变化对增量磁导率信号曲线的影响，考虑到计算结果中增量磁导率信号曲线的特征值与剩磁增量基本成线性关系（或不相关），可以根据剩磁增大时增量磁导率信号曲线的变化情况推断剩磁减小时增量磁导率信号曲线的变化情况。

对上述模拟结果进行总结（表1）如下：随着矫顽力增大，增量磁导率信号曲线的过零点值减小、峰值增大、峰峰距增大，即对应B-H曲线中H=0处曲线斜率减小、B=0处曲线斜率增大、B=0时的H值增大；随着剩磁增大，增量磁导率信号曲线的过零点值增大、峰值减小，即对应B-H曲线中H=0处曲线斜率增大、B=0处曲线斜率减小。

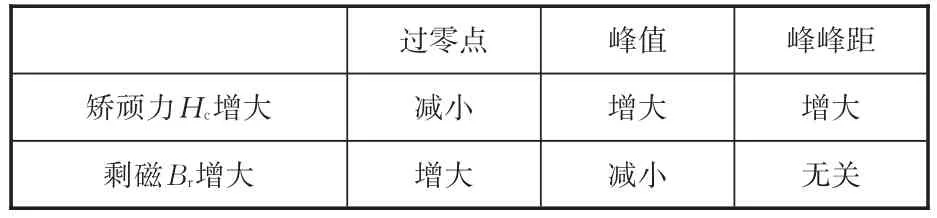
表1 矫顽力、剩磁与增量磁导率曲线特征量的联系Tab.1 Relationships between coercivity，residual magnetism and characteristic quantity of MIP signal curvs

由这些结论可知，通过测量得到某个具有塑性变形的试件及同种材料无塑性变形的试件的增量磁导率信号曲线，将这2条增量磁导率信号曲线进行对比，分析其信号曲线实部的峰峰距、过零点的绝对值和峰值的变化，即可推测发生塑性变形后该试件的B-H曲线中磁感应强度B=0时的外加磁场强度H值、H=0的点处曲线斜率、B=0的点处曲线斜率的变化情况，并推测出发生塑性变形后试件矫顽力和剩磁的变化。简言之，在实际无损检测中，可根据以上描述的规律及检测得到增量磁导率曲线，反推材料的B-H特性的变化，从而判断材料的塑性变形状态。

为了进一步验证计算结果，将本文中数值模拟得到的增量磁导率信号曲线与文献［17］中的实验信号曲线进行比对。需要注意的是：文献［17］中的实验信号曲线为实验得到的信号，本文中的信号为数值模拟的信号；实际加工的碳钢材料具有各向异性和微观状态不均匀性，且具有塑性变形的碳钢试件的微观应力状态具有不均匀性；而本文中使用的数值模拟方法是基于均匀性假设对增量磁导率信号进行模拟，不考虑实际碳钢试件的各向异性和不均匀性；对于碳钢试件的塑性变形，数值模拟中无法直接导入塑性变形量，因而本文改变了计算中导入的B-H曲线，从而反推塑性变形改变导致的B-H曲线及B-H曲线特征量的变化。通过比对可以发现，本文中的数值计算的到的增量磁导率信号曲线与文献［17］中的实验信号曲线形状基本一致。由于计算时采用了将闭口B-H曲线以左右两个饱和点为端点分为中心对称的两部分平滑曲线的处理方式，当外加强磁场达到饱和（约4 000 H/m）时，数值计算信号与实验信号曲线相比有所差别，但是饱和点区域的增量磁导率信号对本文中所讨论的影响规律基本无影响。据此可认为本文采用的数值模拟方法以及得到的结论基本正确。

3 结论

本文针对核电站典型碳素钢材料，研究了基于增量磁导率方法的塑性变形无损评价技术，建立了针对电导率、磁导率均匀的材料的增量磁导率检测信号的数值模拟方法及程序，研究并得到了均匀平板试件剩磁、矫顽力对其相应的增量磁导率信号曲线的影响规律。由这些规律可通过检测得到的增量磁导率信号曲线反推被测试件的塑性变形状态。这些结论对基于增量磁导率方法的材料塑性变形的无损评价具有参考意义。