基于多基因遗传规划的沈阳及其周边地区PM2.5浓度的预测

王晓彤，蒋洪迅

(中国人民大学信息学院，北京 100872)

0 引言

东北老工业区的空气污染问题，既影响经济也危害民生，是当地居民身体健康的一大隐患.[1-5]在诸多空气污染物中，细颗粒物PM2.5的影响非常大.细颗粒物PM2.5指环境空气中空气动力学当量直径小于等于2.5 μm的颗粒物，其在空气中浓度越大，代表空气污染程度越高.相较于其他污染物，PM2.5由于其直径较小，能在大气中停留较久并随气流运动距离较远，对人类的健康影响巨大[6].由于PM2.5等颗粒物的浓度上升，导致全球每年约210万人死于心血管和呼吸道疾病(93%)、肺癌(7%)[7].在我国PM2.5已成为最主要空气污染物之一.因此，PM2.5浓度预测研究，对国计民生具有重要的意义和价值.如果能提供较为准确的预报结果，不仅可以敦促居民进行提前预防，诸如出行佩戴口罩、减少户外活动等，还可以通过预测过程建模和数据挖掘，探索产生高浓度PM2.5的污染来源和形成条件，为空气污染防治提供重要的理论依据和数据支持.

目前，针对PM2.5或者其他空气污染物的预测主要可以划分为数据建模和方法建模两大类：

数据建模是指输入数据的选取和增减，即从数据工程或特征工程的角度出发，研究PM2.5浓度相关的经济、社会、人类行为以及气象条件的数据特征，增减预测模型的输入数据维度和幅度，以探求最优的预测效果.现有的空气质量预测，一般来说，都是在选定某种预测模型或者某几种模型集成的条件，基于现有的历史空气质量数据(如PM2.5，PM10，O3，SO2，CO2等)，再结合对应时空环境下的气象条件数据(如温度、湿度、风速、风向、气压、光照时间等)进行机器学习和训练.

方法建模是指预测方法的调优与改进，即在给定的输入数据不变的情况下，通过对比多个预测模型选择效果较好的方法，或者通过针对某一给定预测模型的方法改进，或者通过参数调优获得更好的预测结果，抑或集成两种或两种以上预测模型以取长补短、提高预测准确度的方法.空气质量预测的方法建模，其主要模型可以归结为多元回归、神经网络和群智能模型等几大类方法.许多学者采用了多元回归模型进行了空气质量预测研究[9-11]；自神经网络出现以来，人们开始使用神经网络模型对空气质量进行预测[12-18]；基于进化计算(Evolutionary Algorithm，EA)的群智能模型，也是预测领域一类重要的研究方法.而遗传规划(Genetic Programming，GP)是相对出现较晚的一种EA方法.不少学者将GP及其变体应用在气象、水文预测等研究领域中，也取得了较好的效果.[19-26]

本文提出一种基于多基因遗传规划(Multi-Gene Genetic Programming，MGGP)的空气质量预测模型，是在经典遗传规划基础上发展出来的一种群进化智能模型，对于多维时间序列预测问题比较有效且具有更强的鲁棒性，特别适合于城市空气质量预测.

1 基于MGGP的空气质量预测模型

遗传规划(Genetic Programming，GP)是遗传算法(Genetic Algorithm，GA)的一个分支，而MGGP是遗传规划的一种鲁棒性变体.为了更好地定义与规范基于MGGP的空气质量预测模型，首先要限定面向预测领域的经典GP模型基本范式和方法框架.

1.1 经典遗传规划模型

GP的基本算法框架与GA相同，都是模仿达尔文的进化论，即选择性地淘汰种群中不适应环境的个体，并从优秀的个体中繁育新一代个体.进化的核心机制是代际更替中的优势个体之间的交叉遗传以及随机变异演化，通过一个预先设定的质量标准形式评判“种群”解集中每个个体适应度，基于此提供被保留到下一代的概率，经过若干次迭代满足终止条件后，可得到一个最优解或近优解.一般来说，终止条件既可以是设定的最高进化代数，也可以是判定的最小误差等适应度(fitness)标准.

GP跟GA相比不同的是可以生成适用问题模型的启发式规则，或者说是其编码形式可具解释性.以最常见的树形编码为例，GP的演化运算是对解析树(parse tree)进行操作，而不是传统地对比特串(bit string)进行操作.PM2.5浓度预测模型的GP编码案例见图1，其编码形式显然具有逻辑上的可解释性，其对应表达式为T(t)/RH(t)-[sin(p(t))+PM(t-1)]，其中T(t)为t时刻的气温，RH(t)表示t时刻的相对湿度，p(t)表示t时刻的气压，PM(t-1)则是上一时刻的PM2.5浓度.一般来说，解析树是由一个终止符集(terminal set，TS)和一个函数集(function set，FS)组成.其中，TS包括函数的各项参数和变量(常数、逻辑常量、变量等)；FS包括基本算术运算、标准编程操作、标准数学函数、逻辑函数或其他数学函数.

已有的研究表明，PM2.5是由空气中原有污染物在一定的气象条件下，经过一系列未知的物理化学过程形成的气溶胶性质悬浮颗粒物.目前已知影响因素中，PM2.5浓度与SO2和NO2等污染物排放及湿度、日照、风力、风向等气象条件有关，甚至与人类活动、地形环境等诸多因素都相关.由于遗传规划GP不仅在复杂非线性回归空间上具有高成功率，而且能够生成适用问题模型的启发式规则表达式，从而为一些潜在的过程提供一些可能的解释，所以GP在空气质量预测领域中特别是PM2.5浓度预测中具有明显的优势.

1.2 MGGP模型

MGGP是传统遗传规划GP的一种变体，即通过线性组合低深度的GP树来提高传统GP的适应性和鲁棒性.[27]由于使用较小的解析树，MGGP有望提供比传统GP更简单的模型[28]. 在MGGP中，预测变量通过多基因程序中的每个基因(即解析树)的加权输出加上偏移项来计算. 例如，MGGP个体使用包括t时刻的气温、相对湿度、气压，上一时刻PM2.5浓度，通过其输入数据的2个基因来预测t时刻PM2.5浓度(见图2)，在数学上，这个模型可以写成

(1)

其中d0为偏移项，d1，d2为回归系数(即每个基因的权重).通常，系数由每个MGGP个体的普通最小二乘法确定[29].因此，MGGP采用经典线性回归方法来捕获非线性行为，而不需要预先指定非线性结构.

在MGGP中，每个基因都是一个简单的GP解析树，不会任何隐含或明确地参考同一染色体中的其他基因.每个初始染色体可能包含一个或几个标准的低深度GP解析树，染色体中基因的最大数量和基因的深度可自行定义.然后，使用标准的子树交叉和变异转换以及直接复制来产生后代.在MGGP中，除了经典的GP子树交叉算子之外，还可以使用被称为“两点高级交叉”的树交叉算子来交换染色体之间的基因.可以设置每个GP运算符的相对概率.

图1 GP的树形遗传编码案例 图2 MGGP个体举例

1.3 基于MGGP的PM2.5浓度预测模型

对于典型回归方法，其模型结构和系数通常在初始阶段就需确定，而在初始阶段如何合理有效确定这些因素却非常困难.而对于MGGP，仅有TS和FS需要初始化，学习方法会自主地找到模型的最佳形式和参数.而且MGGP还有一个优势，它能够自动从输入变量中寻找对模型有利的变量加以使用，并忽略对模型建立没有帮助的变量，有效地减少模型的维度，同时增强模型的可理解性.

1.3.1 变量集TS的设定

考虑因素相关性和数据可获得性，本文选取沈阳地区11个空气质量监测站的PM2.5浓度历史数据、相应时空环境下的气象条件数据作为MGGP模型输入数据.各类数据的类型、符号和单位，如表1所示.

表1 气象学数据及其符号表示

RH即单位体积空气中含有的水汽密度与同温度下饱和的水汽密度的百分比.相对湿度越大，则空气中所含水蒸气越多.由于相对湿度为百分数，故本文用RH(t)表示t时刻的相对湿度的100倍；风向(Wind Direction，WD)是指风吹来的风向，一般以角度表示，正北方向为0°(或360°)，正东方向为90°，正南方向为180°，正西方向为270°，其余风向均由此计算得出，以WD(t)表示t时刻的风向.显而易见的是前一时段的PM2.5浓度与下一时段的PM2.5浓度有着较强相关性，因此，将前一时段PM2.5浓度也作为输入数据之一；用PM(t-1)表示t-1时刻的PM2.5浓度.在后续实验中，实现提前1 d(24 h)、提前2 d(48 h)、提前3 d(72 h)预测当前的PM2.5浓度，表2中提到的t-1时刻在不同实验中分别代表24，48及72 h前的PM2.5浓度.

1.3.2 FS的设定

在函数集中，除了基本的数学四则预算以及IF-THEN条件函数以外，新模型还引入了一元运算符和三元运算符等较为复杂的计算函数.如SQRT表示平方，EXP表示以自然常数e为底的指数函数，ADD3表示三元加法，即3个变量或常数连续相加，MULT3表示三元乘法，即3个变量或常数连续相乘.

1.3.3 基因数的设定

影响MGGP算法性能的相关事项中，一个最主要因素是基因数目.为摸清基因数目对模型预测准确性和算法时间复杂度的影响，本文针对基因数进行了参数尝试的预实验(见图3).结果表明，在提前24 h的PM2.5浓度预测中，基因数目小于5时，均方根误差RMSE随基因数增加而不断降低；基因数目大于等于5的情况下，RMSE变化不再是基因数目的单调减函数，而是偶有反弹波动；随着基因数目的增加，RMSE下降速度逐渐变缓.类似地，在提前48和72 h的浓度预测中，RMSE分别在基因数为6和4时开始上下波动，不再单调递减，且下降速度变缓.

图4描述了不同基因数MGGP模型所需计算时长的变化.显然，随基因数目不断增加，MGGP所用时间整体不断延长.其中，提前24 h的预实验所用时间在基因数为3和8时均有显著的增加；提前48和72 h的预实验时长则分别在基因数为6和7时开始激增；当基因数为10时，3个时段的PM2.5浓度预测所需时长已近似达到基因数目为6时实验所用时间的2倍、基因数目为2时实验所用时间的4倍.

图3 不同基因数目对模型预测准确度的影响 图4 不同基因数目计算时长

综上所述，同时考虑模型准确性和算法复杂性，基因数为6时RMSE相较于基因数为2时已有显著下降，而后下降变缓或反弹，且基因数为6时实验用时显著低于基因数为7～10的情况，故本文选取6作为模型基因数设定.

1.3.4 MGGP模型其他参数的设定

本文提出的MGGP空气质量预测模型的其他各项参数设置见表2.其中：竞争规模是指在每一代种群中选择参与竞争的个体数；竞争规模越大则适应度较弱的个体被选择参与遗传的可能性越小，本文将竞争规模设为15，即在每代种群中选择15个个体进行竞争；精英比例表示每一代中可不进行改变而直接进入下一代的最优个体比例，本文将精英比例设为0.1，则在每代的1 000个个体中，适应度最优的前100个个体可直接进入下一代，而不必进行变换；遗传操作比例是指参与遗传的个体使用不同遗传操作的比例(亦即概率)，本文将变异比例设为14%，交叉比例设为84%，复制比例设为2%.本文使用均方根误差RMSE作为个体适应度衡量标准，RMSE越低，表示预测回归误差越小，适应度越高，本文设置当RMSE降至0.003及以下时，停止进化，否则一直进化至500代.

表2 多基因遗传规划参数设置

在代码实现方面采用GPTIPS2.0工具包作为MGGP的求解平台.GPTIPS2.0是一个基于MATLAB的可完成多基因遗传规划的开源工具包，具有很好的通用性和可扩展性，且不需要其他MATLAB工具包来辅助完成MGGP的实现.[28]

2 实证研究

2.1 实验设置

本文选取沈阳地区11个空气质量监测站，自2016年1月1日0：00到2016年3月26日8：00每小时的各项气象数据及对应PM2.5浓度共22 528组，删去其中信息残缺非常严重的107组数据，使用剩余22 421组数据进行实验.从 22 421组数据中随机抽取20 179组作为训练集，剩余2 242组作为测试集.

在对比实验中，本文将选取BP神经网络和传统GP遗传规划模型作为对照组模型，来衡量MGGP在PM2.5浓度预测中的实际效果.神经网络在PM2.5浓度预测中的表现普遍优于多元线性回归，且BP神经网络作为一种多层前馈神经网络，近年来因其较好的稳定性和准确性而较多地应用于预测领域，并被不断改良使用.[31-34]本文分别使用MGGP和BP神经网络对PM2.5浓度进行全站点和分站点的提前24，48和72 h的预测，并对预测误差RMSE进行比较分析.另外，为体现MGGP相较于传统GP的优势，也使用了GP的PM2.5浓度预测作为对照实验，其参数设置除不使用多个基因外，其他均与MGGP相同.

2.2 MGGP实验过程

针对11个站点的全部数据，在提前24 h的PM2.5浓度预测实验中，种群最优适应度及平均适应度变化见图5.初始种群中，最优适应度为40.149 3，平均适应度为49.601 1，随着种群不断进化，适应度(即均方根误差RMSE)不断下降，由于初始种群是有程序随机生成，误差较大，因此初始几代进化较快，误差迅速减少，随后进化速度渐缓，进化500代后得到最优适应度为38.188.同时，MGGP在进化时优先满足每代种群的最优适应度不断降低，因此在整个进化过程中，各代种群的平均适应度并非是严格的单调递减函数，且收敛相对于最优适应度稍缓，但整体仍呈下降趋势，说明种群在进化过程中不断优化.计算公式为：

-0.000 454 7(x4-1.0x5+x6+cos(x2)+10.69)2-186.6；

(2)

(3)

(4)

0.004 151x2(x2+x6+x3+x4+10.87)+0.002 075x5(x2+10.94)(2.0x2+x4)；

(5)

-0.000 526 3(x2+10.94)(x3+2.0x5)(x3+2.0x5+2.0cos(x2))；

(6)

(7)

最优个体计算公式为：

(8)

表3自变量及其含义对应情况

自变量变量含义 x1p(t)x2T(t)x3RH(t)x4WD(t)x5WS(t)x6PM(t-1)

公式(2)—(7)分别为最优个体的6个基因及偏差项，其中偏差项与第1个基因同在公式(2)中体现，6个基因组成的最优个体用公式(8)表示，其中自变量与具体输入变量含义对应情况见表3.

MGGP提前48 h的PM2.5浓度预测实验中，种群最优适应度及平均适应度变化曲线见图6，初始最优适应度为41.282 5，平均适应度为51.001 2，进化过程中适应度变化趋势与提前24 h的PM2.5浓度预测实验中变化趋势类似，进化500代后最优个体的适应度为38.925 2，略高于提前24 h的PM2.5预测情况.最优个体的6个基因及偏差项计算公式为：

0.000 522 2-x2(x1-1.0x2)(x4-1.0x6)-18.95；

(9)

(10)

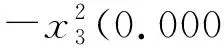
(11)

11.79sin(sin(cos(x5)))；

(12)

0.545 9x2(x4-1.0x6)；

(13)

0.041 37(x3-x5)2+0.041 37x1-0.082 74x4+0.082 74x6+0.279 5.

(14)

最优个体计算公式为：

(15)

图5 MGGP提前24 h PM2.5浓度预测情况 图6 MGGP提前48 h PM2.5浓度预测情况

各自变量及其对应含义见表3.提前72 h的PM2.5浓度预测中，种群最优适应度及平均适应度变化情况见图7，初始最优适应度为41.030 2，平均适应度为50.659 9，进化过程中适应度变化趋势与前两项实验中变化趋势类似，进化500代后最优个体的适应度为38.829 8.最优个体的6个基因及偏差项计算公式为：

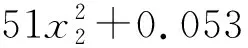
(16)

(17)

(18)

0.000 289 8(x2+x5)(2.0x2+x3)(2.0x2+x4-x6-7.33)；

(19)

(20)

(21)

最优个体计算公式为：

(22)

2.3 对比实验结果

本文使用相同数据对BP神经网络和传统遗传规划GP进行预测训练，得到提前24，48及72 h预测PM2.5浓度最小误差与对应MGGP最小误差进行对比(见表4).从表4可以看出，在PM2.5 浓度预测效果上，MGGP与BP神经网络的预测效果受预测时间间隔的影响较小，在提前24，48或72 h的预测中，均能保证预测误差的相对稳定，相比之下，传统GP则受预测时间间隔影响更大，预测误差随时间间隔增大而不断上升.MGGP与BP神经网络及GP相比体现出了更好的性能，在提前24，48，72 h的浓度预测中产生的误差，MGGP比BP神经网络降低了4%～10%；而传统GP在提前24 h的预测中，误差低于BP神经网络，但在提前48和72 h的预测中，误差明显提高，并高于BP神经网络.此外，MGGP在不同时段PM2.5浓度预测中所产生的误差的标准差比BP神经网络与传统GP降低了13%～63%，体现了MGGP在不同时段PM2.5浓度预测中的鲁棒性优于BP神经网络及传统GP.

表4 MGGP与BP神经网络预测情况对比

MGGP与GP种群进化收敛情况见图8.GP可在100代以内完成收敛，100代之后RMSE下降缓慢，而MGGP从200代后RMSE才开始下降变缓，这是由于MGGP中每个个体由多个基因(解析树)组成种群复杂度高，因此相比于GP收敛稍慢.但因其基因的多样性，虽然GP与MGGP的初始种群均由系统随机产生，MGGP初始的最优适应度却均低于GP，收敛过后3 h段的最终预测准确性均明显高于GP，体现了多基因的种群优势.同时，随着预测时间间隔的增加，二者性能差距不断扩大，MGGP在不同时段的预测中，误差变化较小，尤其在提前48和72 h的预测中，误差相差更小，且提前72 h的预测误差略低于提前48 h的预测误差，说明当预测时间间隔较大时，MGGP几乎不受时间间隔变化的影响；而GP提前48和72 h的预测误差明显高于提前24 h的误差，且提前72与48 h的PM2.5浓度预测误差也相差较大，说明使用MGGP预测PM2.5浓度的鲁棒性也显著优于GP.

图7 提前72 h PM2.5浓度预测情况 图8 MGGP与GP种群进化情况

针对区分站点的PM2.5浓度预测，各个站点数据使用不同预测模型分别提前24，48，72 h的PM2.5 浓度预测结果见表5，其中黑体部分数据表示该站点在该预测时段中不同模型预测结果相比的最佳表现.从表5可以看出，在11个站点3个时段预测的33个预测情形中，MGGP在其中32个情形下的预测误差低于GP及BP神经网络，且稳定性明显优于GP和BP神经网络.同时，在分站点预测的实验中，提前24，48，72 h的预测误差上，GP均大多高于BP神经网络，与全站点中的情况不同；这可能是由于分站点后训练数据显著减少，导致GP生成的预测模型表现明显下降，这也从侧面体现了MGGP比GP的稳定.此外，BP神经网络在分站点的预测实验中偶尔会出现较高的误差，如浑南东路站点提前48 h、京沈路提前72 h及新秀街提前72 h的PM2.5预测误差，RMSE达到了80～90，同样从侧面反映出MGGP较高的稳定性.

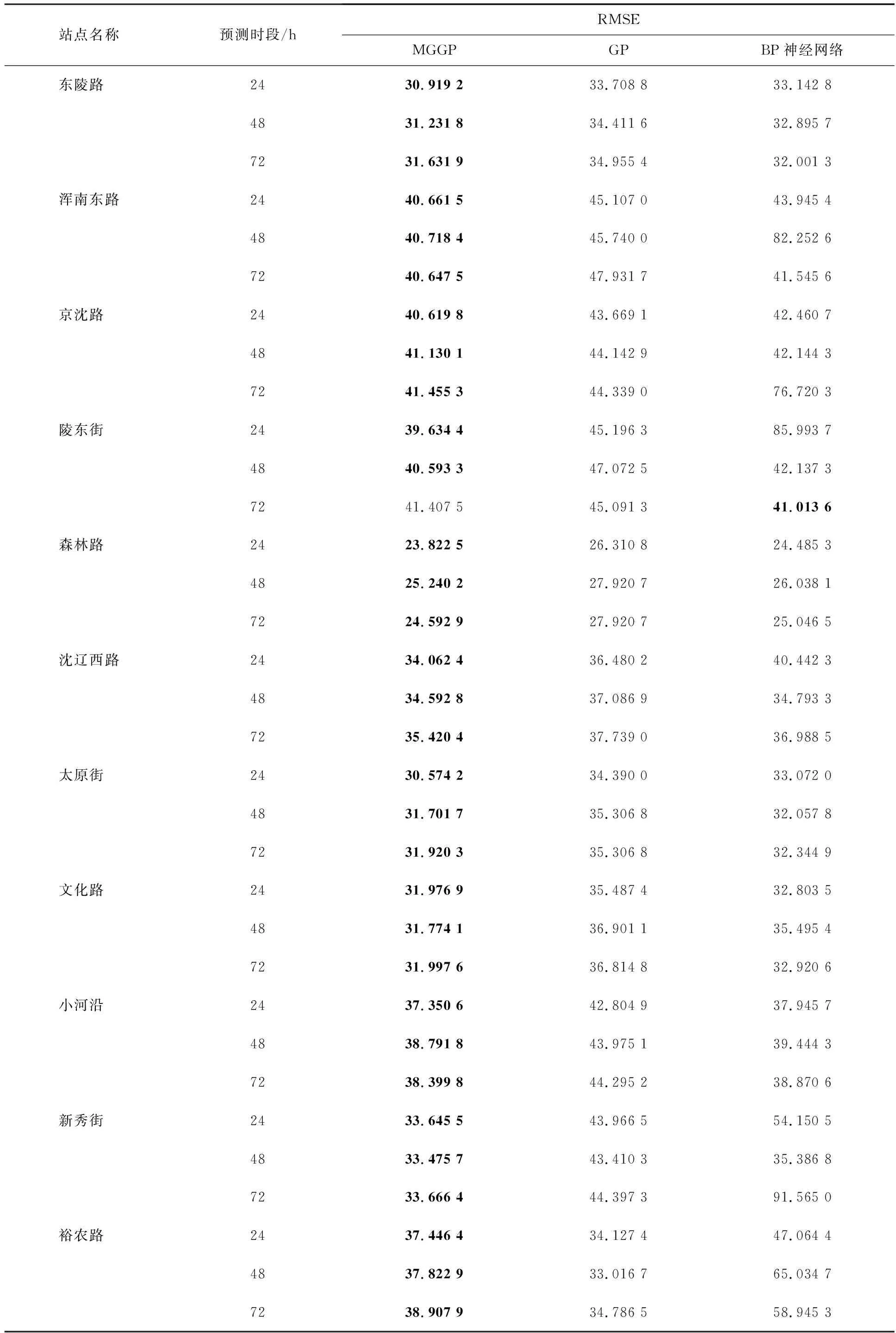
表5 不同站点中不同模型的预测结果对比

3 结论

本文提取气象条件数据及PM2.5浓度历史数据，采用多基因遗传规划MGGP对PM2.5浓度进行了全站点及分站点分别提前24，48和72 h的预测，并与BP神经网络及传统GP的预测水平进行了比较.实验结果表明，MGGP在PM2.5预测上具有较好性能，且预测误差不受时段间隔长短的影响，在不同时段的预测中误差近似，不会因时间间隔的增加而显著降低预测的准确率.相较于BP神经网络，MGGP在性能上具有显著优势，在提前24，48和72 h的预测中均有更小的均方根误差，且在不同站点不同预测时段的误差也绝大多数低于BP神经网络及GP，反映了MGGP对于预测时长变化及空间变化具有更好的鲁棒性.但由于基因数目更多，MGGP比传统GP收敛速度略低.