基于CS-LBP与自适应神经网络的虹膜识别

姜 华，孟丹彤

(东北师范大学信息科学与技术学院，吉林 长春 130117)

虹膜具有稳定性、不可复制性等特点，虹膜识别中的关键步骤就是虹膜特征提取与识别.[1]虹膜特征提取是随着以局部二值模式(Local Binary Patterns，LBP)算子为代表的方法开始而兴起.但LBP算子的维数过高，空间需求过大，因此提出基于中心对称局部二值模式(Center Symmetric Local Binary Patterns，CS-LBP)进行降维[2]，但还是面临维数过大的问题.虹膜识别传统的方法有Hamming距离法[3]，这种算法识别速度虽然快，但在大批量虹膜识别中无法保证识别的准确率.传统的连接权重优化方法容易陷入局部最优的局面.近年来，使用神经网络进行识别的算法开始增多，其中典型的就是BP神经网络.BP神经网络结构复杂，没有固定算法对其结构进行优化，只能具体问题具体分析.

虹膜识别技术常用有一对一(判断2个虹膜是否属于同一种类别)、一对多(从多类别、多图像中判别虹膜的所属类别).本文针对一对一的使用情况，提出采用基于分块中位排序规则的CS-LBP算法提取虹膜纹理特征，并使用BP神经网络进行判断.另外，本文提出混沌系统-选择变异算子-粒子群优化算法(C-SM-PSO)使连接权重可以根据具体虹膜库自适应优化，提高连接权重优化中的全局搜索能力，使神经网络可以自己跳出局部最优，进而提高算法识别的准确率与鲁棒性.

1 虹膜特征提取与识别

1.1 虹膜图像预处理

在提取虹膜特征之前，需要对眼睛图像进行预处理[4].先对眼睛图像进行质量评价，判断其是否可以用于虹膜识别.之后定位虹膜区域，通过归一化将环形虹膜映射到矩形区域，来增强图像清晰度，突出虹膜纹理，水平移位虹膜，消除虹膜旋转的影响.最终截取纹理最强区域，得到252×32维的虹膜图像用于虹膜特征提取.虹膜识别各阶段图像如图1所示.

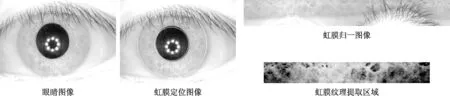
图1 虹膜识别各阶段结果图像

1.2 基于CS-LBP的虹膜特征提取

本文使用CS-LBP对虹膜纹理提取区域进行处理，采用的是基本的3×3型LBP算子，因此产生8位二进制数.处理后的图像为250×30维.将图像分成为30个25×10维的子块，因为每个子块拥有250个值，将每个子块看做一个聚类，找到每个聚类的聚类中心，将其作为子块的代表数，也就是特征值.因为LBP算法反映的是点与周围点灰度值变化的规律，所以中位数可以反映出这一区域中的灰度值整体水平.因此对250个值进行排序，将排序结果的中位数作为子块特征值，最终形成30个特征数，用于虹膜识别.

1.3 基于BP神经网络的虹膜识别

图2 神经网络结构

BP神经网络中的输入层和输出层是必不可少的，因此关于BP神经网络的结构设计的研究主要以隐层数和隐层节点数的设计为主.目前理论上还没有一种确定隐层数和隐层节点数的方法，通常都是根据具体问题具体设计.而关于隐层节点数的设置，在综合考虑网络结构复杂程度、误差大小以及本文实际使用的情况下，用节点删除法[5]确定神经网络的隐层节点数为12.

神经网络结构采用三层，节点数分别为30，12，1.各层之间均采用sigmoid函数作为激励函数[6].神经网络结构如图2所示.

识别过程如下：

将提取出来的测试虹膜与虹膜库中的对比虹膜的30个特征值相减，将差值Ci作为输入层输入神经网络.计算隐层中各节点的输入值公式为

(1)

其中W1-i-t代表输入层到隐层中连接隐层的第i个节点的第t号连接权重，隐层的激励函数采用sigmoid函数，因此得到的隐层中各节点的输出值为

R1-i=1/(1+e-G1-i).

(2)

计算输出层中节点的输入值公式为

(3)

其中W2-t代表隐层到输出层中连接输出层的第t号连接权重，输出层的激励函数采用sigmoid函数，因此得到的输出层的输出值为

P=1/(1+e-S).

(4)

根据sigmoid函数的定义，当2个虹膜属于同一类别的时候，最后的P越接近于1，当二者属于不同类别的时候，P就远离1.最后，根据P设定相应的阈值，进而判断虹膜的类别.

2 C-SM-PSO与连接权重优化

针对BP神经网络的连接权重，本文提出了C-SM-PSO算法进行优化，通过将混沌系统[7]、遗传算法中的变异算子[8]、粒子群算法[9]的有效结合.实现连接权重的自适应优化，并且有助于最终的结果跳出局部最优，同时使用选择算子[10]以达到减少计算量的目的.优化过程流程如图3所示.

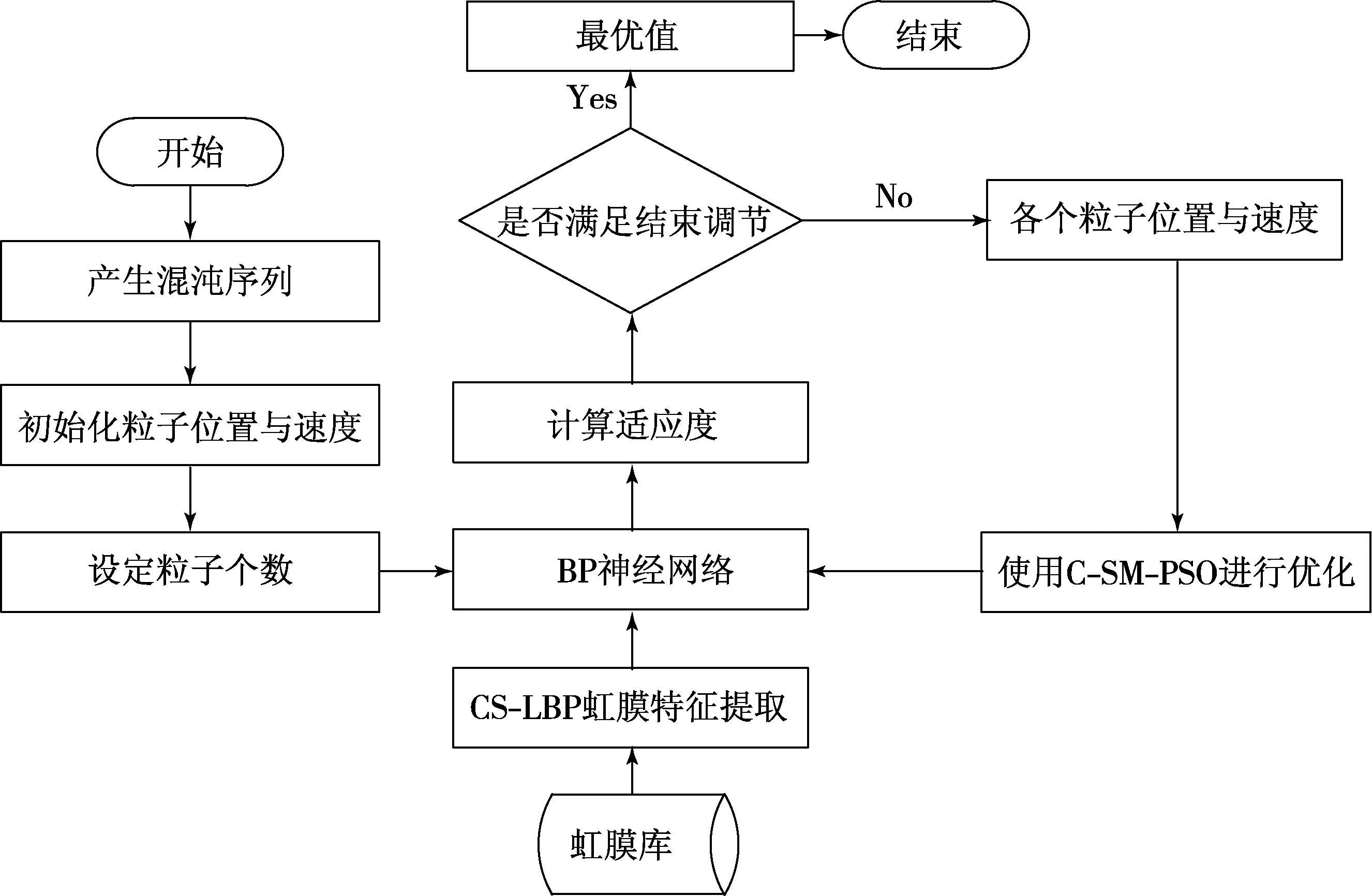
图3 神经网络优化过程流程

本文中的粒子群算法采用10个粒子，每个粒子中包含BP神经网络全部的372个连接权重，相当于设置10个神经网络.先使用随机数确定连接权重以及速度的初始值，初始值设定时加入干扰粒子的混沌系统，以达到不改变原有粒子群算法在初始粒子时的随机性条件下利用改进后算法混沌性的目的.本文初始化使用的是改进式(初始化的范围为[-n，n])，初始化后进行300次的迭代，初始化公式为

(5)

其中tk代表需要初始化的粒子位置(文中为各连接权重的大小)和速度.初始速度和大小采用随机数的方式设置.训练时，根据不同的虹膜库进行自适应训练，每个虹膜库训练出一组合适的连接权重.考虑训练时间复杂度等因素，本文在连接权重训练时，采用1个训练虹膜与20个对比训练虹膜组成的训练集(其中5个虹膜与训练虹膜为同类别，其余15个虹膜为不同类别)分别用10组神经网络进行虹膜识别.根据最后输出层的输出值P计算适应度.适应度函数公式为

(6)

其中Pi与Pt分别表示异类别与同类别的输出层输出值.正常情况下，同类虹膜输出值应该接近于1，异类虹膜输出值应该远离1.因此用异类虹膜与1的差值平方除以同类虹膜与1的差值平方，最后得到的适应度F越大越好.

根据适应度的结果，设定并更新粒子的历史最优位置pBest以及全局最优位置gBest，首次迭代的时候，将10个粒子的初始连接权重设为各粒子的pBest.之后的299次迭代中，神经网络通过将F与历史最优的F进行比较，如果新的F比历史最优的F大，那么将pBest的值更换为这个神经网络的连接权重，比较10个神经网络的F，F最大的神经网络的粒子中的连接权重设为gBest.之后对粒子的速度与位置进行更新.更新公式为：

(7)

(8)

进化完速度和位置后，使用选择算子和变异算子进行变异，用随机选择法[12]从372个连接权重中选择100个(输入层到隐层之间选择95个，隐层到输出层之间选择5个)进行变异操作，变异操作主要根据变异概率Pm判断该粒子是否进行变异.一旦粒子发生变异，粒子的值将更换一个区间进行设置，这个区间与实现设置的初始区间不同，根据不同区间设置粒子大小，进而使得粒子群跳出原有布局，增加跳出局部最优的能力.变异概率Pm(Pm为实数)根据不同的虹膜库而设定，本文设置在(0.05，0.09)之间效果较好.变异操作公式为

(9)

其中T表示需要变异的粒子(位置与速度)，粒子一旦变异，新的变异区间为[m1，m2]，具体区间根据不同虹膜库进行设定.经过300次迭代后，将最后的全局最优值gBest中的连接权重用做最终识别.

3 实验与分析

本文使用的CPU主频为双核2.5 GHz，内存为4 GB，操作系统为Windows 7、64位.并且识别实验所用的虹膜与参数训练所用的虹膜不同.ROC曲线与正确识别率(Correct Recognition Rate，CRR)是评价算法常用的指标，ROC曲线表示错误拒绝率(False Reject Rate，FRR)与错误接收率(False Accept Rate，FAR)的关系.FRR与FAR相等的值称为等错率(Equal Error Rate，EER).ROC曲线越接近坐标轴，EER越小，算法的性能越好[13].

3.1 算法性能比较实验

实验中使用中国科学院CASIA-V1、CASIA-Iris-Twin虹膜库中质量评价合格的虹膜组成测试虹膜库(测试集).将本文算法与其他几种情况进行对比，根据CRR、EER以及ROC曲线分布情况进行比较：(1)仅使用PSO算法对BP神经网络进行优化，测试混沌系统与选择变异算子对识别的影响；(2)不使用其余优化算法，依照BP神经网络结构、人工优化连接权重，观察不同的自适应优化方式对识别的影响；(3)Li的SCCS-LBP+Hamming法(统计特征中心对称局部二值模式+海明距离)[14].测试集虹膜个数以及每个算法所进行的类内、类外以及总匹配次数如表1所示.测试不同LBP类识别方法的各个算法的CRR与EER如表2所示.

表1 不同虹膜库匹配次数

表2 不同虹膜库匹配结果 %

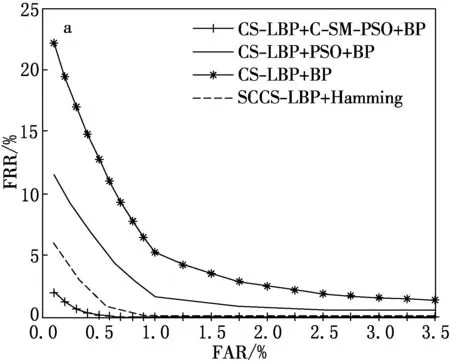
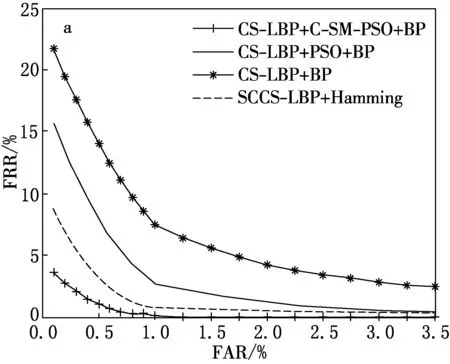
CASIA-V1的ROC曲线如图4所示.CASIA-Iris-Twin的ROC曲线如图5所示.

全局图 局部图

全局图 局部图

根据表2以及图4和5可以看出，本文算法根据虹膜库的自适应优化对虹膜识别起到了积极影响.因为本文算法不需要人工过多的干预，只需要更换虹膜库的时候更改相关配置即可，优化效果更好.另外，混沌系统与选择变异算子的加入，使得粒子群可以在原有设定范围外进行设置，加大了参数的活动范围，使粒子群更容易跳出局部最优化，有助于参数的全局搜索.另外，与文献[14]的算法相比，虽然二者的CRR相差不大，但是EER却要更低，ROC曲线也更贴近于横、纵坐标轴.

3.2 与传统经典算法比较实验

实验使用中国科学院CASIA-V2、CASIA-Iris-Lamp虹膜库中质量评价合格的虹膜组成测试虹膜库(测试集).将本文算法与Gabor滤波+Hamming算法[15]、Haar小波过定点检测法[16]、基于改进的Log-Gabor小波的虹膜识别算法[17]进行对比.这3种是虹膜识别中经典算法及改进算法.测试与非LBP类的虹膜识别算法相比较.测试集虹膜个数以及每个算法所进行的类内、类外以及总匹配次数如表3所示.各个算法的CRR与EER如表4所示.

表3 不同虹膜库匹配次数

表4 不同虹膜库匹配结果 %

CASIA-V2的ROC曲线如图6所示.CASIA-Iris-Lamp的ROC曲线如图7所示.

全局图 局部图

全局图 局部图

从表4、图6和7可以看出，与传统的虹膜识别算法及其改进算法相比，本文算法仍然具有一定的优势.因为Hamming距离是根据阈值进行分类，但由于虹膜拍摄条件的复杂性，仅凭一个阈值是很难对大批量虹膜进行判别.因此，本文算法运用了神经网络要相对占一些优势.而文献[17]的算法针对提取特征的Log-Gabor进行了改进，使得准确率得以提升，但是还是较本文算法有一些差距.同时也可以看出，使用不同的虹膜库以后，本文的CRR还能保持较高水平，EER也较低，说明本文算法具有良好的稳定性与鲁棒性.

4 结束语

本文提出基于CS-LBP与自适应神经网络的虹膜识别算法，以CS-LBP提取虹膜特征，提出分块中位排序规则反映虹膜图像灰度值变化规律.并用三层BP神经网络进行虹膜识别，神经网络的连接权重采用C-SM-PSO算法、根据不同的虹膜库进行自适应优化，根据虹膜库自适应优化连接权重，提高连接权重优化中的全局搜索能力，使神经网络可以自己跳出局部最优，提高算法通用性以及识别准确率.采用CASIA-V1与CASIA-Iris-Twin虹膜库的正确识别率达到99.97%和99.94%，等错率分别达到0.39%，0.62%.而且ROC曲线更贴近横、纵坐标轴.与传统虹膜识别算法相比，本文算法也具有一定的优势.

本文算法仅针对神经网络的连接权重进行了优化，针对学习策略、网络结构没有涉及.并且针对图像的光照与噪音干扰等问题也没有涉及，这两点将是下一步研究的重点.