基于校验矩阵的BCH码译码方法的研究
姜恩华,马 琳
(淮北师范大学物理与电子信息学院,安徽 淮北 235000)
BCH码是循环码的一个子类,属于线性分组码的范畴.对于二进制本原的BCH码,在给定码长n的条件下,可以根据纠错能力t,设计出二元本原BCH码.BCH码通用的经典译码算法是Berlekamp(BM)迭代译码算法.[1]近年来,BCH被应用于北斗系统中,并提出了相应的译码算法.[2-4]本文借助无噪条件下的压缩感知理论[5-7],提出了BCH码的一种译码方法,该方法通过收码R和校验矩阵H求出伴随式S,把S作为测量信号、H作为测量矩阵,通过基追踪BP算法重构出差错图案E,把E与收码R进行模2加运算,求出发码C的估值. 本文研究了BCH码的校验矩阵H的稀疏度Spark和约束等距性RIP[8-9],设计了基于校验矩阵H的BCH码译码的仿真实验方案,以(15,5)、(15,7)、(31,16)和(31,21)BCH码为例,通过误码率和码字C重构的成功率,分析比较了本文提出的算法和BM迭代译码算法的译码效果.
1 校验矩阵H
1.1 校验矩阵的构成
BCH码的校验矩阵H可以通过生成矩阵G的系统形式直接生成[10],公式为
G=[Ik,P],H=[PT,In-k],
(1)
BCH码的生成矩阵G可以通过其生成多项式g(x)求出.根据BCH码的码长n和信息元组长度k,通过MATLAB语句bchgenpoly(n,k)直接求得生成多项式g(x). 以(15,7)BCH码为例,通过MATLAB函数bchgenpoly(15,7)求得生成的多项式为
g157(x)=x8+x7+x6+x4+1.
(2)
根据生成多项式g157(x),求出其生成矩阵G,化简为系统形式G157,根据(1)式,求出其校验矩阵H157,公式为:
(3)
(15,7)BCH码的纠错能力t为2,有1位和2位差错的收码R能够被纠正,即差错图案E的稀疏度K的最大值为2,由(3)式可知,校验矩阵H157的稀疏度Spark为5.[11]
1.2 校验矩阵的性质
对于随机差错来说,BCH码的差错图案E可以看做是一维稀疏数字信号,只要差错图案E的稀疏度K小于或等于纠错能力t,就可以在译码时实现对收码的纠错.完全纠错时,稀疏度K与纠错能力t的关系为
K≤t.
(4)
定理1校验矩阵H的稀疏度Spark与纠错能力t的关系为
Spark(H)≥2t+1.
(5)
证明校验矩阵H的稀疏度Spark为校验矩阵H中线性相关的最小列数,若BCH码的最小距离为dmin,校验矩阵H线性无关的最大列数为dmin-1[10],所以,校验矩阵H线性相关的最小列数为dmin,而BCH码的最小距离为dmin≥2t+1,所以(5)式成立.
定理2校验矩阵H的稀疏度Spark与差错图案E的稀疏度K的关系为
Spark(H)≥2K+1.
(6)
证明把(4)式代入(5)式求得(6)式成立.
定理3校验矩阵H满足2K阶约束等距性RIP,其中K为差错图案E的稀疏度.即任意从校验矩阵H抽出2K列必线性无关.
证明根据(4)式可知,BCH码的最小距离dmin≥2K+1,由定理1可知,校验矩阵H线性无关的最大列数为dmin-1,从校验矩阵H任意抽取2K列必线性无关,所以校验矩阵H满足2K阶约束等距性RIP.
可以验证(15,7)BCH码的校验矩阵H157满足定理1、定理2和定理3.(15,7)BCH码的纠错能力t为2,有1位和2位差错的收码R能够被纠正,即差错图案E的稀疏度K的最大值为2,由(3)式可知,校验矩阵H157的稀疏度Spark为5,可以验证校验矩阵H157的稀疏度Spark符合定理1和定理2,满足2K阶的约束等距性RIP.
2 基于校验矩阵H的BCH码译码方法
2.1 求解校验矩阵
根据BCH码的码字C的长度n和信息分组m的长度k,借助MATLAB函数bchgenpoly(n,k)求得BCH码的生成多项式g(x),根据g(x)求出(n,k)BCH码生成矩阵G的系统形式,然后求出(n,k)BCH码的校验矩阵H,把校验矩阵H作为压缩感知理论中的测量矩阵.
2.2 求解测量信号
由收码R和校验矩阵H,通过(7)式计算出伴随式S,把伴随式S作为压缩感知理论中的测量信号,公式为
S=R·HT.
(7)
2.3 求解差错图案
欠定方程为
S=E·HT.
(8)
(8)式有n个未知数,有n-k个方程.把S代入(8)式,求解差错图案E.
在二元域内,每个伴随式S,可以代入(8)式求出2k个差错图案E,根据最佳概率译码的准则,选取重量最轻的E作为其估值.
在二元域内,差错图案E的重量为差错图案E中1的个数,即差错图案E的l0范数或l1范数的值,求重量最轻的差错图案E为求差错图案E的l0范数或l1范数的最小值.可以借助压缩感知理论,把伴随式S作为测量信号,校验矩阵H作为测量矩阵[12-13],通过压缩感知重构算法求解差错图案E的l0范数或l1范数的最小值,重构差错图案E的压缩感知模型为:
min‖E‖0s.t.H·ET=ST;
(9)
min‖E‖1s.t.H·ET=ST.
(10)
求解(9)式可以采用OMP重构算法,求解(10)式可以采用基追踪BP重构算法.本文选用基追踪BP算法根据(10)式重构出差错图案E.
2.4 求解码字C的估值
把差错图案E与收码R进行模2加运算,由
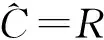
(11)

3 BCH码译码仿真实验
3.1 仿真实验设计
由于BCH码属于线性分组码,所以可按照线性分组码的编译码过程实现基于校验矩阵的BCH码的编译码实验设计[10].首先,借助BCH码的生成多项式求出其生成矩阵G和校验矩阵H.其次,随机产生10 000个信息分组m,按照C=mG生成BCH码的码字;码字C也可以调用MATLAB的函数bchenc生成[14].再次,对码字C进行2PSK调制,已调信号通过高斯白噪声信道AWGN,信噪比SNR取值为0~12 dB,每个SNR点取10 000个码字.最后,在接收端对接收信号进行2PSK解调,得到收码R;代入式(7)求出伴随式S,把S作为测量信号,校验矩阵H作为测量矩阵,通过基追踪BP算法[15-16]重构出差错图案E,将E与收码R进行模2加运算,求得码字C的估值;也可以调用MATLAB函数bchdec译码[10],求得码字C的估值,函数bchdec采用BM迭代译码算法实现译码.仿真实验方案如图1所示.通过误码率和码字C重构的成功率分析译码效果.

图1 线性分组码的编码和译码过程
3.2 纠正2位错误的BCH码的译码效果分析
以(15,7)和(31,21)BCH码为例,按照仿真实验步骤,借助MATLAB软件编写脚本程序,进行仿真实验,分别采用BP算法和BM迭代译码算法完成译码,仿真实验求得的误码率如图2所示,码字重构的成功率如图3所示.

图2 纠正2位错误的BCH码译码的误码率 图3 纠正2位错误的BCH码重构码字的成功率
从图2可以看出,相同码长n情况下,BP算法的误码率低于BM迭代译码算法;当SNR为8 dB 时,BP算法的误码率低于10-4;当SNR为9 dB时,BM迭代译码算法的误码率低于10-4.从图3可以看出,相同SNR情况下,BP算法的重构码字的成功率高于BM迭代译码算法,当SNR为6 dB时,BP算法的重构码字的成功率近似为100%;当SNR为7 dB时,BM迭代译码算法的重构码字的成功率近似为100%.
3.3 纠正3位错误的BCH码的译码效果分析
以(15,5)和(31,16)BCH码为例,分别采用BP算法和BM迭代译码算法完成译码.按照仿真实验步骤,编写MATLAB脚本程序进行仿真实验,误码率如图4所示,码字C重构的成功率如图5所示.
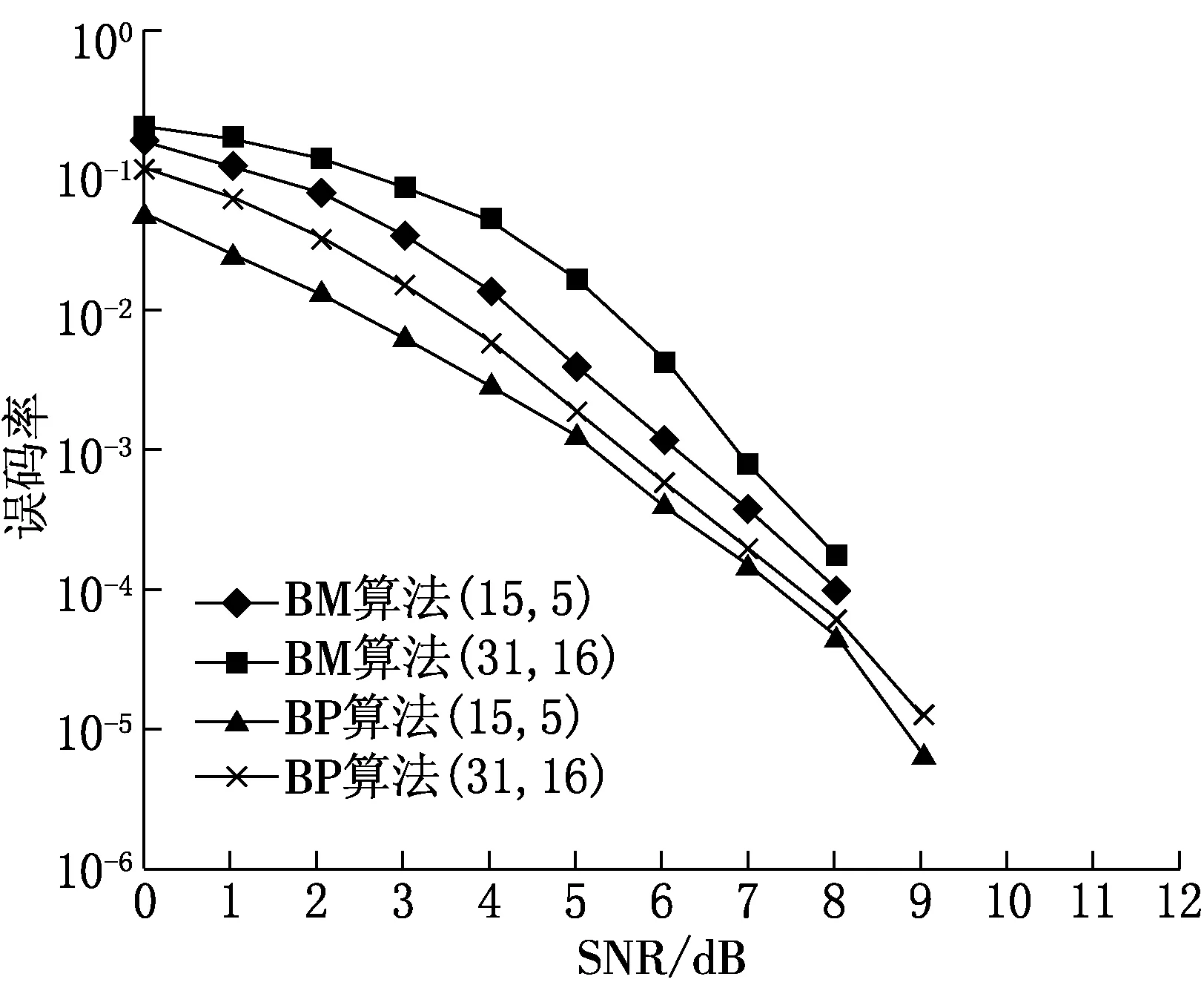
图4 纠正3位错误的BCH码译码的误码率 图5 纠正3位错误的BCH码重构码字的成功率
从图4可以看出,相同信噪比SNR条件下,基追踪BP算法的误码率低于BM算法,当SNR为9 dB时,基追踪BP算法的误码率低于10-4,BM迭代译码算法译码的误码率近似为10-4.从图5 可以看出,相同信噪比SNR条件下,基追踪BP算法的重构码字的成功率高于BM迭代译码算法;当SNR为6 dB时,基追踪BP算法重构码字的成功率近似为100%;当SNR为7 dB时,BM迭代译码算法重构码字的成功率近似为100%.
4 结论
本文提出了基于校验矩阵的BCH码译码方法.首先,证明了校验矩阵H满足压缩感知的测量矩阵的2K阶约束等距性RIP,并提出了3个定理;其次,提出了重构BCH码差错图案E的压缩感知模型;再次,设计了基于校验矩阵的BCH码译码实验方案,以纠正2位错误的(15,7)和(31,21)BCH码和纠正3位错误的(15,5)和(31,16)BCH码为例,分析比较了基追踪BP算法和BM迭代译码算法的译码效果.仿真实验表明,基于校验矩阵的BCH码译码方法是可行和有效的.

