Ni/Au/n-GaN肖特基二极管可导位错的电学模型∗

王翔 陈雷雷 曹艳荣 羊群思 朱培敏 杨国锋王福学 闫大为 顾晓峰

1)(江南大学电子工程系,物联网技术应用教育部工程研究中心,无锡 214122)2)(西安电子科技大学,宽带隙半导体技术国家重点学科实验室,西安 710071)(2018年4月21日收到;2018年7月2日收到修改稿)

1 引 言

GaN肖特基二极管往往存在远大于理论值的过剩泄漏电流,将严重降低器件的整体电学性能和可靠性[1].微观电学和形貌测试表明,泄漏电流的产生与位错所形成的特定缺陷态直接相关[2,3].然而,由于这些电学缺陷主要位于材料内部无法直接实验探测,许多研究者仅将其等效为禁带内的连续可导缺陷态.实际上,这种简单模型忽略了缺陷对材料电学行为的影响,不利于理解真实的电荷输运过程和电流退化物理本质.与此相关,一些研究者对GaN肖特基二极管的反向泄漏电流的输运机制提出了多种物理模型[4−7].例如,Miller等[3]认为,低温下反向泄漏电流主要由隧穿电流占主导,而高温下缺陷辅助隧穿电流或者变程跳跃电流将占主导.Zhang等[5]认为,低温下的反向泄漏电流主要由电子Fowler-Nordheim(FN)隧穿过程决定,而高温下电子从表面施主态Frenkel-Poole发射至连续可导缺陷态过程将变得更加重要.Lei等[6]通过数值拟合证明,电子直接隧穿进入导电位错有关的连续态可能是决定泄漏电流行为的主要过程.此外,Hashizume等[7]认为,势垒层表面高浓度深能级施主态(N空位)能够导致势垒变薄和电场增强,使FN隧穿过程更加容易发生.然而,该模型与N空位通常为浅能级施主的事实相冲突,且没有考虑位错对泄漏电流的影响,实验证据不足.以上物理模型有助于理解GaN肖特基结构泄漏电流的输运本质,但都没有提出足够清晰的可导位错电学物理模型,具体的物理过程仍未被一致认同.

鉴于此,本文基于对GaN肖特基二极管泄漏电流输运机制的分析,提出一个精细可导位错的唯像电学物理模型.该模型主要强调:1)位于位错中心的深能级受主态电离后具有较高的库仑电势,基本不对漏电流有贡献;2)位错周围的浅施主缺陷态电离后具有较低的库仑势,且耗尽区变薄,可导致显著的FN隧穿电流;3)并非传统N空位,而是O替代N形成的浅能级施主态可能为导致泄漏电流的主要电学态,其激活能大约为47.5 meV.

2 器件制备与测试

器件所采用的GaN外延片是利用金属有机化学气相沉积法生长在自支撑GaN体衬底上的,其外延结构包括0.5µm n+-GaN过渡层和3µm n-GaN有源层.图1(a)所示为外延片的阴极射线发光图(CL mapping),其中每一个黑点对应一个垂直线性位错(非辐射复合中心).据此,可获得外延片的平均位错密度约为5×106cm−2,远低于常规蓝宝石衬底GaN外延片的典型值108cm−2.图1(b)所示为器件的横截面结构示意图.首先,利用标准光刻和lift-off工艺定义欧姆电极形状和尺寸;接着,利用电子束沉积Ti/Al/Ni/Au合金后在750°C的氮气环境中快速热退火60 s以形成欧姆接触;然后,利用等离子体化学气相沉积技术在半导体表面生长20 nm的SiO2介电层;最后,利用标准光刻和lift-off工艺定义圆形肖特基电极形状和尺寸(直径约为160µm),在HF和HCl的混合液中浸泡30 s后使用电子束沉积Ni/Au层形成肖特基电极.图1(c)所示为最终制备的Ni/Au/n-GaN肖特基二极管器件的正面照片.图2所示为器件的高频1/C2-V曲线,通过其斜率可知有源层内的有效施主掺杂密度约为4×1016cm−3,通过其截距可知器件的内建电势和肖特基势垒高度分别约为1.18 V和1.34 eV.

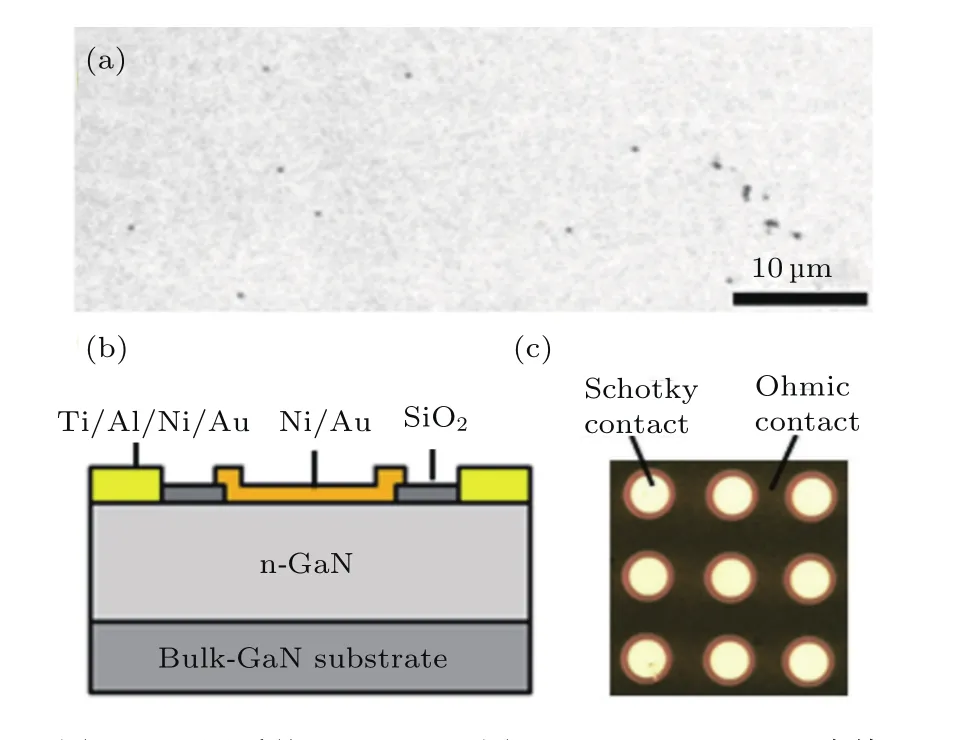
图1 (a)同质外延GaN CL图;(b)Ni/Au/n-GaN肖特基二极管器件横截面结构示意图;(c)器件的俯视图Fig.1.(a)CL image of the homoepitaxial GaN wafer;(b)schematic cross-section diagram of the fabricated Ni/Au/n-GaN Schottky diode;(c)top view image of the devices.

图2 Ni/Au/n-GaN二极管的高频1/C2-V数据图Fig.2.High frequency 1/C2-V data plot of Ni/Au/n-GaN diodes.

3 结果与讨论

图3(a)所示为GaN肖特基二极管的变温电流-电压(T-I-V)特性曲线,测试温度范围为300–400 K.可以看到,在正向偏压下,半对数坐标下的电流先线性增长,然后由于串联电阻效应增强而逐渐向下弯曲.通常,肖特基二极管的T-I-V关系可由以下经验公式近似描述[8]:

式中I0为反向饱和电流,可由线性关系外延至V=0的电流截距获得;ϕB为电流势垒高度;k为玻尔兹曼常数;RS为串联电阻;n为理想因子,可由线性I-V曲线的斜率获得;T为温度;q为电子电量.当I0主要由热电子发射(thermionic emission,TE)电流占主导且隧穿电流和耗尽层复合电流不重要时,n接近于1.当掺杂浓度较大或在低温时,隧穿电流将成为主要电流成分,I0和n值都会增加[9].图3(b)所示为n和I0对T的依赖关系,可以看到,随着T从300 K升高至400 K,n由1.78逐渐下降到1.37,而I0由1×10−11A逐渐增加至8.24×10−10A.由于I0的数值远大于理论值1×10−15A,同时考虑到空穴的势垒高度较大(约2.12 eV),所以I0的温度依赖特性不能使用经典TE机制或产生复合机制解释.此外,既然I0表现为T的强函数,故单纯的非热隧穿机制也不适用.

图3 (a)Ni/Au/n-GaN肖特基二极管的典型变温I-V特性曲线;(b)n和I0对T的依赖关系Fig.3.(a)Typical T-I-V curves of Ni/Au/n-GaN Schottky diodes;(b)n and I0as a function of the temperature.

线性位错(尤其是螺旋位错)被普遍认为是引起较大泄漏电导的主要原因,那么相关的电学缺陷必须是施主型,因为施主态电离后才能够导致较低的势垒,并为电子的传导提供空态.此观点与Look等[10]的结论一致.在此背景下,(1a)式的形式可重写为

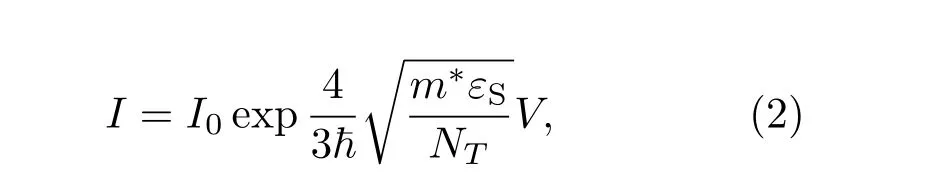
式中m∗～0.2m0是电子在GaN中的有效质量;ħ为约化普朗克常数;NT为电离的净施主态密度,可由线性关系的斜率获得.(2)式表明,可以通过电流斜率获得NT的数值.

图4(a)所示为NT对1/T的依赖关系. 可以看出,随着T从300 K升高至400 K,NT从4.1×1018cm−3增加至6.9×1018cm−3,其对应的激活能约为47.5 meV.由于NT的数值远大于材料的背景浓度(4×1016cm−3),表明在施主态位置形成了薄表面势垒区.同时,根据(1b)式可以获得ϕB值约为1.1 eV,如图4(b)所示.该值比电容法获得的势垒高度低0.21 eV,表明肖特基界面的势垒和电导分布并不均匀.因此,我们认为正向低偏压区的泄漏电流应主要为高密度施主态所导致的局域隧穿电流(n＞1).

在反向偏压下,耗尽层内电场将变得更强,使表面势垒更薄而形成三角形势垒.此时,金属电子将具有很大概率隧穿到半导体内部,形成FN隧穿电流[11],有

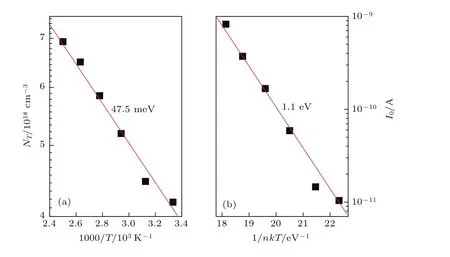
图4 Ni/Au/n-GaN肖特基二极管的(a)施主态密度和(b)反向饱和电流的Arrhenius数据图Fig.4.Arrhenius plots of(a)the net density of the donor-like impurities and(b)the saturation current in Ni/Au/n-GaN Schottky diodes.

式中A为有效隧穿面积,ϕ为有效隧穿势垒高度,E为最大电场强度.重写(3)式得.

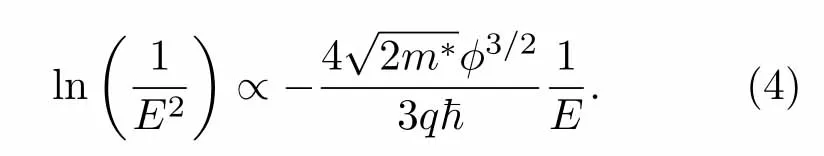
(4)式表明,当FN隧穿电流占主导时,实验ln(I/E2)-1/E数据应满足线性依赖关系[12],且斜率为T的弱函数.图5(a)所示为由实验数据得到的ln(I/E2)-1/E数据,结果与(4)式的形式完全一致,证明反向泄漏电流应主要为FN隧穿电流.与Hashizume等[7]的假设一致,为了得到一个理想的拟合结果,施主态分布必须具有指数衰减的形式,其特征长度约为4 nm,如图5(b)所示.通过拟合数据,可获得有效隧穿势垒高度约为0.8 eV.该值低于之前的电流势垒高度1.1 eV,这可能是缺陷存在使局域电场降低所导致.必须指出的是,这里经典Frenkel-Poole发射过程并不重要,因为电流斜率的温度系数比理想结果要大5倍.

图5 (a)不同温度下的ln(I/E2)-1/E数据图;(b)施主态缺陷的空间分布Fig.5.(a)The experimental ln(I/E2)-1/E plot at different temperatures;(b)the distribution of donor-like impurity concentration as a function of the depletion depth.

N空位被认为是GaN材料中最重要的浅能级施主态.然而,我们认为O替代N形成的ON缺陷应是引发较大泄漏电流的主要原因,因为:1)材料生长过程中,O原子倾向于向{10¯10}表面通过N空位进行扩散并在位错终端积累,形成高密度的ON-VGa复合物,影响位错的电学特性[13];2)第一性原理计算得到的O有关施主态的激活能大约为50 meV[14,15],非常接近本文得到的实验值47.5 meV.

较多的理论计算和实验结果表明,Ga空位在GaN材料内具有较低的形成能,常作为深能级受主态稳定地存在于位错中心位置.不难推测,这些深能级受主态能够俘获周围施主态的自由电子,抬升该处的库仑势,同时降低周围施主态的电势,形成如图6所示的能带结构[16−18].因此,位错中心主要带负电[19],对泄漏电流应该没有贡献,而位错周围高浓度的浅能级施主态能够形成势垒高度较低的薄耗尽区,为正电性,可以作为有效的泄漏电流隧穿通道.该位错电学模型与实验观察结果一致[20],即泄漏电流主要发生在位错的周围边缘区域.根据我们所提出的模型,被降低的导带应为泄漏电子的主要输运通道,因为电子很容易从浅能级施主态激发至迁移率更高的导带.相比简单连续缺陷态物理模型,我们所提出的电学模型物理意义更加丰富,这对于研究其他GaN基器件的泄漏电流输运机制以及器件可靠性与失效性都具有重要意义.

图6 GaN可导位错的能带结构示意图Fig.6.Schematic bandgap diagram around the electrical dislocation site in GaN.

4 结 论

通过深入分析GaN肖特基二极管的泄漏电流输运机制提出了一个可导位错的电学模型,认为位错中心主要为带负电的深能级受主态,对泄漏电流基本没有贡献;位错周围的高浓度浅能级施主态则会形成局域的有效隧穿通道,决定整个器件的电流行为.因此,有效钝化O有关的施主态(或者减小位错周围的N缺陷空位)是有效减小此类器件泄漏电流的有效方法之一[21].