墙壁反射中子对脉冲堆波形的影响∗
高辉 宋凌莉 李兵
(中国工程物理研究院核物理与化学研究所,绵阳 621900)(2018年1月12日收到;2018年5月30日收到修改稿)
1 引 言
金属型脉冲堆[1,2]及临界装置运行时,会受到堆厅以及堆芯周围反射体的影响,表现为堆参数发生变化,比较明显的例子是瞬发中子衰减常数α.金属型装置一般存在本征的α,由于反射体的存在,就不存在本征值了,其衰减曲线并非是单一的指数函数,变得非常复杂[3,4].当堆芯的瞬发中子衰减时间特性与反射中子的时间特性存在较大差异时,其反射中子的影响就会变得非常明显,对于实验精度要求较高的临界实验或脉冲堆实验,必须考虑环境反射中子影响[4,5].
金属型脉冲堆代时间一般为ns量级,中国快中子增殖反应堆(CFBR-II)爆发额定脉冲时,功率的前沿上升周期为50µs,脉冲半高全宽为180µs,脉冲坪持续时间约20 ms.为了获得宽时间尺度的反射中子对脉冲堆爆发脉冲的影响,研究了反应堆大厅墙壁的反射中子效应.CFBR-II堆厅存在很厚的水泥墙,在爆发脉冲过程中,墙壁的反射中子会回到堆芯参与链式反应,因而会引起脉冲波形的变化,主要表现在脉冲波形的后沿衰减变慢和脉冲坪的抬高.也有观点认为墙壁反射中子是造成反应性定向差(超缓发临界的反应性刻度结果与超瞬发临界测量结果存在的差异)的关键因素之一.因此研究墙壁的反射中子对脉冲堆的脉冲特征参数有重要的意义.
墙壁的反射中子是一个反射层的问题,处理反射层的问题经常用到双区模型,早期Avery[6]和Cohn[7,8]把多个区域转化为裂变的堆芯区域和非裂变的反射区域,这个模型被称为Avery-Cohn双区模型.Spprigs和Busch[9−11]在前人的基础上提出了通过中子在堆芯和反射层之间的概率关系得到耦合参数,双区之间通过泄漏概率耦合在一起,解释了中子寿命、反应性等参数.Dam[12]将双区模型应用到强反射体的零功率装置上,解释了一些参数;Tobias等[13]采用双群的方法计算了一个重水慢化的系统获得了临界参数.Aboanber[14]在双区模型的基础上增加了能群的结构.Kawai[15,16]应用类似的模型,在动力学方程中增加了表示反射体反馈效应的微扰项并应用于平板型反应堆的求解.综上,传统的双区模型均是建立在裂变区和反射区的平衡关系上,可以很好地处理稳态问题,对于脉冲堆爆发脉冲这类瞬态问题则不适用.
因此,早期的研究墙壁反射中子不用双区模型,一般采用缓发中子法,即把反射中子的行为看作是几组缓发中子来处理[17,18],虽然得到了某些与实验结果一致的参数,但是缓发中子的行为与反射中子的行为存在明显的差异.近期,李兵等[19,20]把反射中子以时间常数的形式引入点堆动力学方程,分析了反射中子对反应性、脉冲产额、脉冲波形等参数的影响.在此基础上,我们提出了采用等效源[21]的方法来处理反射中子,将双区模型进行了扩展.金属脉冲堆的泄漏中子接近裂变谱,因为能量的连续分布,反射中子返回堆芯的时间是分散的,即中子是陆陆续续的返回,而不是同时回到堆芯,如果把墙作为反应堆的一部分进行计算时,得到的反应性是墙壁与金属堆芯充分平衡后的结果,而爆发脉冲是一个动态过程,其时间远小于平衡时间.若要精确地描述墙壁反射中子的贡献,必须考虑时间延迟效应.本文提出了一种将反射中子等效为本征中子源的时间关联双区模型,可有效解决反射中子的问题.
2 含反射效应的点堆方程
根据Fuchs-Hansen模型[22],爆发脉冲过程中的中子数满足下面的方程组:
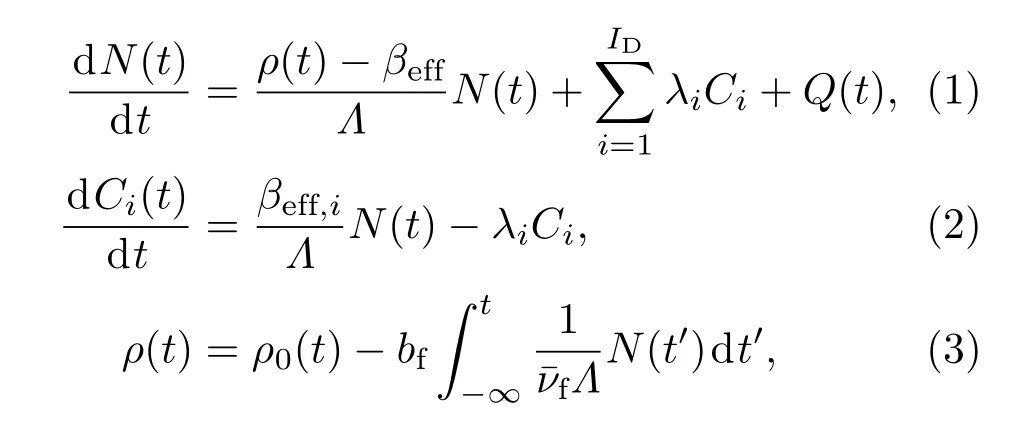
式中,N(t)表示堆内中子数;ρ(t)为系统反应性;ρ0为系统的初始反应性;βeff为缓发中子有效份额;Λ为系统中子代时间;ID为缓发中子分组数;λi为第i组缓发中子衰减常数;Ci为第i组缓发中子先驱核数;Q(t)为源强;βeff,i为第i组缓发中子份额,有为关闭系数,表示每次裂变引起的反应性的变化,对于同一个脉冲堆其bf是固定的,可以采用温度系数的方法进行计算和实验测量;¯νf为平均每次裂变放出的瞬发中子个数.方程(1)和(2)是包含缓发中子的点堆动力学方程,方程(3)是热膨胀效应产生的反应性变化.
脉冲堆动力学方程的求解,一般是假定瞬发反应性与α呈线性关系,即α=ρp/Λ,这样中子数的变化只与前一时刻的中子数和当前的反应性有关.但由于反射中子的存在,并且具有明显的延迟效应,中子数的变化率不仅与前一时刻的中子数有关,还与整个中子数变化过程有关.即早期的中子经过泄漏、反射再回到堆芯,对当前时刻的中子数产生影响.因此上述的点堆动力学方程不能直接求解.因为中子与中子之间的相互作用可以忽略,那么链式反应导致的中子数变化率与中子源导致的中子数变化率是可以分离的.据此把反射中子作为一种特殊的源处理,把反射中子等效为金属系统的本征源Q(t),其能谱、分布、返回效率等因素统一考虑在等效关系中,只保留时间的信息,这样点堆动力学方程将仍然适用,相关的动力学参数取裸堆情况下的参数.这样,一个金属堆芯加墙壁的复杂系统转变成简单的金属系统,而求解动力学方程的关键是这个特殊源Q(t)的获得.
3 堆芯泄漏中子的等效性处理
首先考虑一个泄漏中子经过反射,再返回堆芯引起的堆芯内中子数的变化.我们采用随机中子输运程序计算一个定态的裸堆芯的状态,获得关键参数瞬发中子增殖常数α和泄漏率P.然后计算金属堆芯加堆厅墙壁的结构,计算一个泄漏中子经过反射返回堆芯,引起的中子数变化,忽略缓发中子效应,结构模型如图1所示.在堆芯表面建立一个球面源,模拟泄漏中子,采用泄漏中子的能谱,发射方向为球面向外.在t=0时刻,一个泄漏中子从堆芯表面出发,以一定的概率再次返回堆芯,统计t时刻的堆芯内的中子数nr(t)随时间的变化.
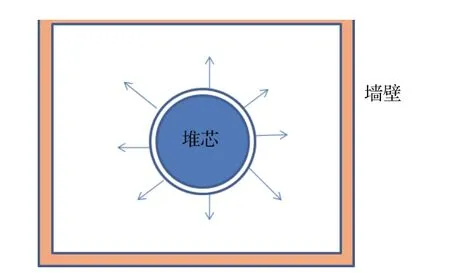
图1 计算模型示意图Fig.1.Schematic diagram of calculating model.
计算结果如图2所示.为了方便后续处理,我们对nr(t)进行了平滑处理,按幂级数进行拟合,图中实线所示.金属堆芯泄漏一个中子后,存在一定的概率被反射回来,也有可能多次来回反射,模拟的最终结果就是每一个泄漏中子引起堆内中子数变化nr(t),是一个概率统计的平均结果.考虑到金属堆芯系统适用点堆模型,因此可以反解出引起nr(t)的本征源.

图2 堆内中子数Fig.2.Number of neutron in reactor core.
令一个泄漏中子的等效源强为qe(t),堆芯的瞬发中子衰减常数为α,那么由点堆方程可知,
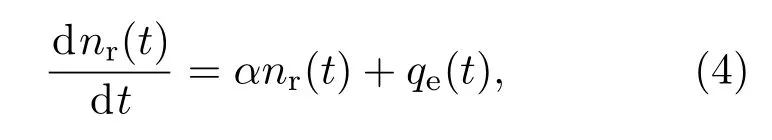
(4)式可变形为
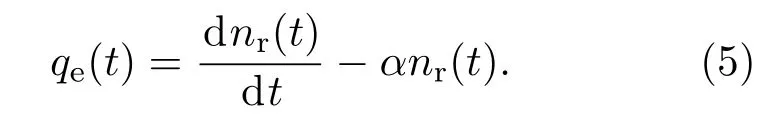
因为nr(t)已经计算得出,采用数值方法对其进行微分,即可得到一个泄漏中子的等效源qe(t),如图3所示.可见反射中子大部分在1µs左右的时间返回,但是其后续返回的中子持续的时间较长.这就是一个泄漏中子的等效中子源强,与系统反应性无关.

图3 一个泄漏中子等效源qe(t)Fig.3.Equivalent source of one leakage neutron qe(t).
若要求解爆发脉冲这个动态过程,需要知道所有泄漏中子的等效,这样才能利用点堆方程来求解.令爆发脉冲过程中t′时刻系统内的中子为那么就是单位时间内泄漏中子数.那么t时刻的总的等效源强Q(t)为

式中P为泄漏率,Λ堆型中子代时间.可以看出等效源强与中子数的历史有关,而不仅仅是与前一时刻的中子数有关.
4 考虑反射中子的脉冲堆波形
获得了反射中子的等效源后,把Q(t)代入方程(1),联立方程(2)和(3),编写点堆方程数值求解程序,便可获得脉冲波形,如图4所示.脉冲的前沿周期为50µs时的波形,黑色虚线为没有考虑反射中子的情况,蓝色实线为考虑反射的计算结果,红色曲线是实验测量数据.可见反射中子明显地改变了脉冲波形,使其后沿衰减变慢,抬高了脉冲坪的功率.
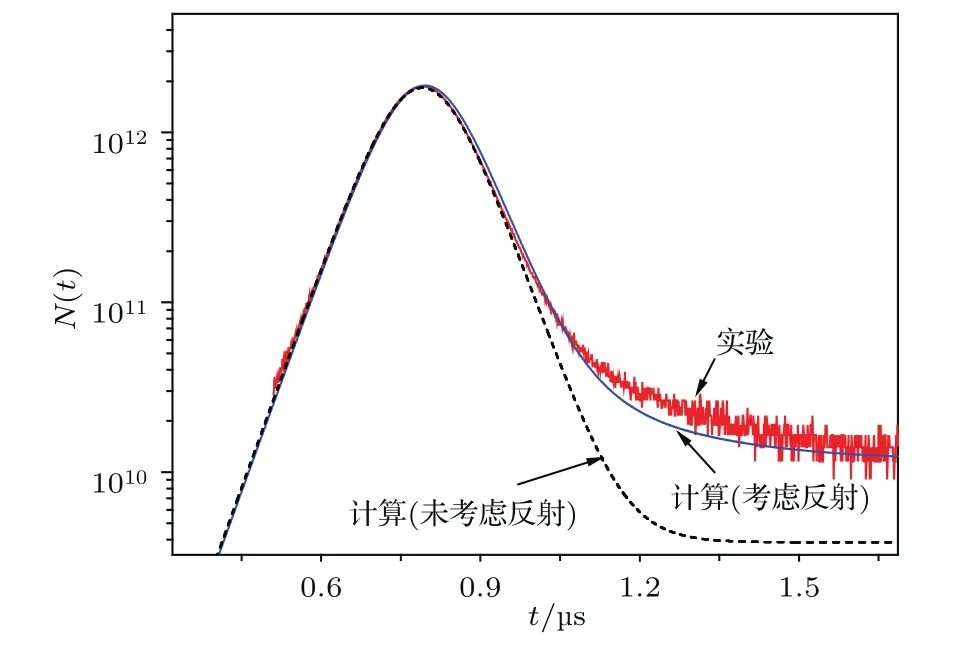
图4 脉冲波形Fig.4.Waveform of burst.
5 结 论
采用等效源方法对反射中子进行本征源等效处理,建立了包含反射中子时间信息的点堆动力学方程,用该方程求解脉冲堆爆发脉冲过程的波形与实验结果一致.结果表明,墙壁引起的反射中子导致了脉冲堆波形后沿衰减变慢和脉冲坪功率提高.反射中子的等效处理方法还可用于反射体对反应性扰动和瞬发中子衰减常数的影响研究.

