外电场和双轴应变对MoSH/WSi2N4肖特基结势垒的调控*

梁前 钱国林 罗祥燕 梁永超 谢泉

(贵州大学大数据与信息工程学院,新型光电子材料与技术研究所,贵阳 550025)

鉴于实验上最新合成的二维半导体材料WSi2N4(WSN)和二维金属材料MoSH(MSH),构建了金属-半导体MSH/WSN 肖特基结.在实际的金属-半导体接触应用中,肖特基势垒的存在严重降低了器件的性能.因此,获得较小的肖特基势垒甚至是欧姆接触至关重要.本文使用第一性原理计算研究了在外电场和双轴应变作用下MSH/WSN 肖特基结势垒的变化.计算结果表明,外电场和双轴应变均可以有效地调控MSH/WSN肖特基结势垒.正向外电场能实现MSH/WSN 肖特基结p 型与n 型肖特基接触之间的动态转化,而负向外电场可实现MSH/WSN 肖特基结向欧姆接触的转化.此外,较大的双轴应变可实现MSH/WSN 肖特基结p 型与n 型肖特基接触的相互转化.此项工作为基于WSN 半导体的肖特基功能器件及场效应晶体管提供理论指导.

1 引言

2004 年,石墨烯成功从块体石墨中被剥离出来[1],它展现出优异的电子、光学、力学和机械特性以及超高的延展性[2-4],同时,它在室温下具有超高载流子迁移率[5](约为25000 cm2·V-1·s-1).但是,石墨烯零带隙的特性限制了其在电子器件方面的应用,人们开始把目光转向别的二维材料: 过渡金属硫化物(transition metal dichalcogenides,TMDCs)[6-9]、六方氮化硼(h-BN)[10-12]、黑磷(BP)[13,14]等,这些新兴的二维材料在纳米电子学、光电子学、谷电子学、自旋电子学和储能技术等方面有着极其诱人的潜力[15-18].随后,范德瓦耳斯异质结的出现更是带来了相对于其他单层二维材料更诱人的前景.范德瓦耳斯异质结保留了每层二维材料的固有电子特性,具有独特的电子和器件性能,在纳米电子和光电子器件制造等领域中逐渐取代了石墨烯和其他单层二维材料.

2020 年,Hong 等[19]通过化学气相沉积(chemical vapor deposition,CVD)成功合成了自然界不存在的新型层状二维材料MoSi2N4(MSN)及其衍生物WSN,七原子层结构带来了相比于其他二维材料更优异的性能,许多基于MSN 的研究就此展开.他们还采用第一性原理计算预测了一个全新的MA2Z4家族,其中M代表了过渡金属元素(Mo,W,V,Nb,Ta,Ti,Zr,Hf,或Cr),A代表了Si 或Ge 元素,Z代表了N,P 或As 元素,它们均在动力学上稳定.Wu 等[20]通过在MSN 和WSN 双层上施加外加电场和双轴应变,发现压缩应变能实现该双层结构从间接带隙到直接带隙的转变,而外加电场可实现该双层结构从半导体性到金属性的转变,表明MSN/WSN 双层结构有望成为下一代纳米电子和光电子新材料.最近,Qian 等[21]和Zang等[22]通过在MSN 和WSN 中引入N 空位缺陷,发现MSN 和WSN 表现出高效的析氢反应(hydrogen evolution reaction,HER)催化活性,相对于本征MSN 和WSN 有了质的提升,表明含有N 空位缺陷的MSN 和WSN 可作为HER 催化剂.

近年来,有着Janus(即古罗马神话中的“双面神”,暗指两个相对面上具有不对称性质)结构的二维材料引起了人们的兴趣.这种Janus 结构的材料打破了原本结构所具有的对称性,带来了新颖独特的性质.许多Janus 二维材料也被制备出来,例如可以在化学沉积生长MoS2或WS2多层过程中注入Se 来合成MoSSe 或WSSe[23].MoSSe 结构正好处于MoS2和MoSe2之间,由于其对称性的打破,使得MoSSe 表现出不同于MoS2和MoSe2的性质.2021 年,Janus MoSH(MSH)通过H2等离子体处理的方式被成功合成[24].简单来说,MSH仅仅是将MoS2最外面的一层S 原子替换为H 原子,但两者不同的是,MoS2是一种带隙值约为1.80 eV 的二维半导体材料,而MSH 却是一种无带隙的二维金属性材料.同时,Janus MSH 被证明在动力学上是稳定的且具有高的载流子浓度,意味着MSH 在金属-半导体接触方面具有巨大的潜力[24].近来,Liu 等[25]发现,Janus 材料由于其对称性打破产生的固有内建电场,产生了一个不对称势,进而增强了从Janus 材料到石墨烯层光生载流子分离和转移的速率,表明Janus 异质结材料相较于传统异质结材料在高能量转换效率的光伏电池应用等方面具有更大的潜力.在金属-半导体接触时,Janus 材料的两个面具有不同的功函数,不同界面接触行为有着不同的肖特基势垒和电流传输等特性,其肖特基势垒的可调谐性对未来肖特基器件的制造有着重要的影响.

鉴于MSH 和WSN 的很多工作尚未展开,本文使用第一性原理计算研究了外电场和双轴应变对MSH/WSN 肖特基结势垒的调控作用,探究n 型与p 型肖特基的接触之间的转换或者肖特基与欧姆接触之间的转换,为实验提供理论指导.首先,构建了两种接触模型: MSH 的S 面与WSN 接触的MHS/WSN 模型和MSH 的H 面与WSN 接触的MSH/WSN 模型.然后,分别研究了肖特基结的两个单层和两种肖特基结模型的电子能带特性,发现肖特基结的能带仅仅是两个单层能带的简单叠加.紧接着,研究了它们的电荷转移特性,还计算了它们的束缚能,MHS/WSN 与MSH/WSN肖特基结的束缚能分别是-1.635 eV,-1.648 eV.本文选取相对更稳定的H 面接触的MSH/WSN模型来通过外电场和双轴应变进行肖特基势垒调控.结果表明,外电场和双轴应变均可有效调控肖特基结势垒高度,合适的外加电场或双轴应变可实现肖特基的p 型与n 型接触之间的转换,甚至是肖特基结向欧姆接触的转换.本工作揭示了基于WSN 的MSH/WSN 肖特基结在肖特基功能器件制造方面有着巨大的潜力.

2 计算方法

本文的所有第一性原理计算使用了基于密度泛函理论下的VASP(Viennaab initiosimulation package)软件包[26,27].采用了广义梯度近似(generalized gradient approximation,GGA)下的Perdew-Burke-Ernzerhof(PBE)泛函[28]来描述相互作用电子间的交换关联能.投影缀加平面波(projector augmented wave,PAW)[29]方法被用来描述离子实和价电子之间的相互作用.经过收敛性测试后,选择500 eV 的截断能和 9×9×1 的K点网格.能量和力的收敛标准分别被设定为 1×10-6eV和0.01 eV/ Å.为了得到更精确的结果,采用DFTD3 方法修正层与层之间的范德瓦耳斯力.为了避免周期性对相邻映像的影响,增加了20 Å的真空层.

3 结果与讨论

3.1 电子结构特性

图1(a)和图1(c)分别展示了MSH 和WSN的侧视图和俯视图.从图1(a)可以看出,MSH 与MoS2有着相同的结构,只是把其中一层S 原子替换成了H 原子.从WSN 的侧视图和俯视图可看出,WSN 有着独特的N-Si-N-W-N-Si-N 七原子层特性,W 原子处于由Si 原子与N 原子组成的六元环的中心.优化后的MSH 和WSN 的晶格参数分别为3.01 Å 和2.91 Å,计算结果与前人结果相符[24,30].构成异质结后晶格失配率为3.32%,满足晶格失配率小于5%的要求.从图1(b)MSH 的能带图可以看出,费米能级与能带交叠,MSH 显示出金属性.而图1(d)WSN 的能带图中费米能级位于导带和价带中间,WSN 显示出半导体性.WSN 的价带顶和导带底分别位于布里渊区里不同的点:Γ点和K点,因此 WSN 属于间接带隙半导体,带隙值为2.09 eV,其值与前人计算结果2.076 eV[19],2.06 eV[31]接近,也说明了我们实验模型的可靠性,数值的差异是由于计算精度的不同与赝势的选取不同而造成.

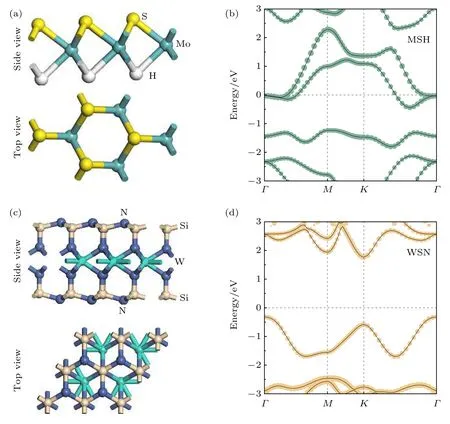
图1 (a)MSH 与(c)WSN 的侧视图与俯视图;(b)MSH 与(d)WSN 的能带结构.费米能级被设置为0 点Fig.1.Top and side views of(a)MSH and(c)WSN;band structures of(b)MSH and(d)WSN.The Fermi level is set to zero.

然后,构建了由二维金属MSH 与二维半导体WSN 组成的肖特基结模型,由于MSH 由两个不同的面组成,分别构建了两种不同的接触模型:S 面与WSN 更靠近的MoHS(MHS)/WSN 肖特基结模型和H 面与WSN 更靠近的MSH/WSN 肖特基结模型.MHS/WSN 与MSH/WSN 肖特基结的侧视图见图2(a)和图2(c),其中白色小球代表H原子,黄色小球代表S 原子.MHS/WSN 与MSH/WSN 肖特基结的俯视图见图2(b)和图2(d),H 原子和S 原子位于WSN 中N 原子正上方.结构优化后,测得MHS/WSN 与MSH/WSN 肖特基结最优层间距分别为3.48 Å与3.75 Å,表明MSH 层与WSN 层之间存在微弱的范德瓦耳斯相互作用.为了探究MHS/WSN 与MSH/WSN 肖特基结的稳定性,分别计算了两种异质结构的束缚能(binding energy,Eb),Eb的大小由以下公式确定:Eb=EvdW-EMSH(MHS)-EWSN.其中EvdW代表组成肖特基结之后的能量,EMSH和EWSN分别代表着MSH(MHS)和WSN 单层的能量.经过计算,MHS/WSN 与MSH/WSN 两种肖特基结的束缚能Eb的大小分别是-1.635 eV,-1.648 eV,均为负值,说明两种肖特基结都是稳定的.束缚能Eb的值越小其构成的肖特基结越稳定.MSH/WSN 肖特基结的束缚能小于MHS/WSN 肖特基结的束缚能,因此选用更稳定MSH/WSN 肖特基结来研究外电场和双轴应变对异质结肖特基势垒的影响.

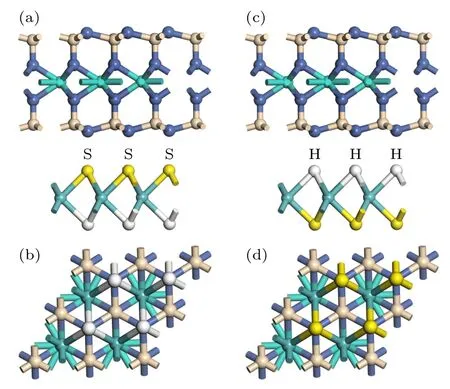
图2 (a)MHS/WSN 与(c)MSH/WSN 肖特基结的侧视图;(b)MHS/WSN 与(d)MSH/WSN 肖特基结的俯视图Fig.2.Side views of(a)MHS/WSN and(c)MSH/WSN Schottky-junctions.Top views of(b)MHS/WSN and(d)MSH/WSN Schottky-junctions.

首先,在图3(a)和图3(d)绘制了MHS/WSN与MSH/WSN 肖特基结的投影能带图,其中绿色和黄色线条分别代表MSH 和WSN 对肖特基结的贡献.两张能带图只有细微的差别,在能带的走势上几乎一致.单层MSH 和WSN 原本的特性被很好地保留下来,肖特基结的能带只是两个单层MSH和WSN 的简单叠加,两个肖特基结中WSN 依旧保持了间接带隙半导体的特性.根据Schottky-Mott 规则,半导体n 型和p 型肖特基势垒高度由以下公式来计算:ΦBn=ECBM-EF;ΦBp=EF-ECBM.如果ΦBn的值大于ΦBp的值且都大于0,说明在界面处形成了p 型肖特基接触;如果ΦBn的值小于ΦBp的值且都大于0,说明在界面处形成了n 型肖特基接触;如果半导体的ΦBn或者ΦBp的值小于0 或者费米能级与半导体的导带或者价带有交叠,说明在金属与半导体界面处形成欧姆接触.计算所得的MHS/WSN 与MSH/WSN 肖特基结的ΦBn值分别为1.38 eV 与1.54 eV,ΦBp值分别为0.60 eV 与0.37 eV,因此,两种肖特基结在界面处均形成了p 型肖特基接触.

如图3(b)与图3(e)所示,为了探究金属层MSH 和半导体层WSN 界面间的电荷转移,绘制了平面平均差分电荷密度图.平均差分电荷密度Δρ由以下公式定义: Δρ=ρvdw-ρMSH(MHS)-ρWSN.其中ρvdw,ρMSH(MHS)和ρWSN分别代表肖特基结、MSH(MHS),WSN 单层沿Z平面的平面平均电荷密度.结果发现,由于MSH 本身所特有的Janus结构特性,WSN 分别与不同的面接触时电荷转移的程度会不同.在图3(b)与图3(e)中,正值代表了电荷的积累,负值代表了电荷的耗尽.不管是对于MHS/WSN 还是MSH/WSN 肖特基结,电荷均在WSN 层耗尽,在MSH 层聚集,不过MSH/WSN肖特基结电荷转移的程度要稍微大于MHS/WSN肖特基结.电荷的积累和扩散行为是电荷重新分布的结果,会形成一个微弱的内建电场,内建电场的方向由WSN 层指向MSH 层.图3(c)与图3(f)展示了MHS/WSN 与MSH/WSN 肖特基结的有效静电势.可以观察到二维金属材料MSH 和二维半导体材料WSN 之间存在着电势差,这也印证了由于电荷转移在MSH 与WSN 层之间存在着一个微弱的内建电场.此外,由于MSH 是Janus 材料,在S 面和H 面存在着电势差,而WSN 显示出完美的对称性.

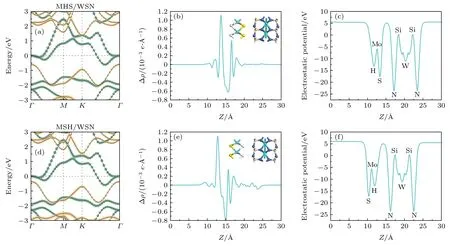
图3 (a)MHS/WSN 与(d)MSH/WSN 肖特基结的投影能带结构;(b)MHS/WSN 与(e)MSH/WSN 肖特基结的两个界面之间沿Z 平面的平面平均差分电荷密度;(c)MHS/WSN 与(f)MSH/WSN 肖特基结的有效静电势.其中绿色和黄色线条分别代表了MSH 和WSN 对肖特基结的贡献,费米能级被设置为0 点Fig.3.Projected band structures of(a)MHS/WSN and(d)MSH/WSN Schottky-junctions.Plane-averaged differential charge densities between two interfaces along Z-plane of(b)MHS/WSN and(e)MSH/WSN Schottky-junctions.The effective electrostatic potential of(c)MHS/WSN and(f)MSH/WSN Schottky-junctions.The green and yellow lines represent the contributions of MSH and WSN,respectively.The Fermi level is set to zero.

3.2 电场对肖特基势垒的调控

施加外加电场是一种能够有效地调控肖特基势垒的方法,这里定义施加外加电场的正方向是从WSN 层指向MSH 层,与内建电场的方向一致.图4 为不同外加电场下MSH/WSN 肖特基结的投影能带结构,外加电场的范围从-0.4 V/Å到+0.4 V/Å.结果发现,在负外加电场作用下,WSN 导带底和价带顶的位置都发生上移,而在正外加电场作用下,WSN 导带底和价带顶的位置都发生下移.负外加电场作用下,从-0.1 到-0.3 V/Å,导带底仍然位于K点,价带顶位于Γ点,与之前单层时候一致.而在-0.4 V/Å外加电场作用下,其导带底的位置由原来的K点转移到了M点.在正外加电场作用下,其导带底和价带顶的位置并未发生变化,保持了原先单层间接带隙半导体的特性.

图4 不同外加电场下MSH/WSN 肖特基结的投影能带结构(-0.4 -+0.4 V/Å),费米能级被设置为0 点Fig.4.Projected band structures of MSH/WSN Schottky-junctions under different external electric fields(ranging from -0.4 to 0.4 V/Å).The Fermi level is set to zero.

图5(a)展示了其肖特基势垒随外加电场变化的折线图,当施加正外加电场大于0.2 V/Å时,ΦBp的值逐渐超过了ΦBn的值,MSH/WSN 肖特基结由原来的p 型接触变为了n 型肖特基接触.当施加负外加电场大于-0.2 V/Å时,ΦBp的值从正变为负,意味着MSH/WSN 肖特基结变为了欧姆接触.欧姆接触对于传统的基于金属-半导体接触的场效应晶体管的制造有着很深远的意义,此项工作可以为基于WSN 半导体的肖特基功能器件及场效应晶体管提供理论指导.此外,ΦBn的值随着正外加电场的不断增大而减小,随着负外加电场的不断增大而增大,ΦBp的变化趋势刚好与之相反.虽然外加电场引起了ΦBp和ΦBn的变化,但ΦBn与ΦBp的和几乎没有发生改变.唯独在施加-0.4 V/Å时的外加电场作用下ΦBn与ΦBp的和有些许的下降(下降了大约0.15 eV),这是由于电场引起了导带底位置发生改变而引起的.

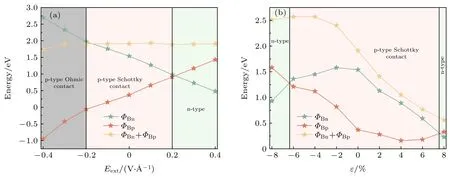
图5 MSH/WSN 肖特基结在不同(a)外电场(Eext)和(b)双轴应变(ε)下的肖特基势垒的变化Fig.5.Variation of the Schottky barrier heights under different(a)external electric fields(Eext)and(b)biaxial strain(ε)in MSH/WSN Schottky-junction.

3.3 双轴应变对肖特基势垒的调控

除了外电场,双轴应变是另一种有效调控肖特基势垒的方法.双轴应变的应变系数ε定义为:ε=(a-a0)/a0×100%,其中a和a0分别代表应变后和应变前的晶格系数.如果应变系数ε的值大于1,代表拉伸应变;反之,如果应变系数ε的值小于1,代表压缩应变.图6 给出了在不同双轴应变(-8%-8%)下MSH/WSN 肖特基结的投影能带结构.当施加-2%的双轴应变时,导带底的位置由原来的K点转移到了M点;负双轴应变程度继续加大到-4%时,价带顶的位置由原来的Γ点转移到了K点;而当负双轴应变程度继续加大到-8%时,导带底的位置转移到了不属于布里渊区里Γ→K路径上某一点处.当施加正双轴应变时,导带底的位置向下移动,价带顶的位置先向上移动后向下移动,但导带底和价带顶的位置仍分别位于K点与Γ点.而且,不论是正双轴应变还是负双轴应变,它们都保持了WSN 原本间接带隙半导体的特性.

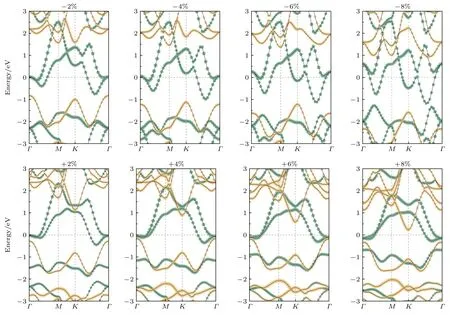
图6 不同双轴应变ε 下MSH/WSN 肖特基结的投影能带结构(-8%-+8%),费米能级被设置为0 点Fig.6.Projected band structures of MSH/WSN Schottky-junctions under different biaxial strain ε(ranging from -8% to 8%).The Fermi level is set to zero.

图5(b)展示了MSH/WSN 肖特基结势垒随着双轴应变变化的折线图.在正双轴应变下,ΦBn的值随着应变强度的增大而减小,ΦBp的值先减小而后在到达4%的时候增大;在负双轴应变下,ΦBn的值先增大后在达到-4%应变强度后减小,而ΦBp的值呈现一直增大的趋势.与外加电场不同的是,由于双轴应变极大地改变了异质结的晶格参数,导致其ΦBn与ΦBp的和发生较大改变.ΦBn与ΦBp的和在-4%到+8%应变强度范围内逐渐减小,在-8%到-4%范围内逐渐增大.当应变强度达到一个较大的值(±8%)的时候,MSH/WSN 肖特基结可实现从p 型到n 型肖特基接触之间的转变.外电场和双轴应变引起MSH/WSN 肖特基结势垒的变化的原因可以归结为: 异质结的电子结构由重叠的电子轨道控制,而施加的外电场和双轴应变可以极大地影响电子轨道的重叠行为.价电子轨道在导带底和价带顶占据主导地位,外电场和双轴应变通过影响价电子轨道的重叠行为影响导带底和价带顶价电子的电子态发生改变使得导带和价带发生移动.

图7 设计了一个基于二维MSH/WSN 肖特基结的可调谐肖特基二极管,其中向下的箭头代表正外加电场的方向,向上的箭头代表负外加电场的方向.由于MSH 具有高的载流子浓度,二维金属MSH 它可以被用作电极以实现高效的载流子注入.通过改变外部电场的强度和方向,肖特基二极管可以被重新配置,以实现欧姆接触与肖特基接触和p 型与n 型肖特基接触之间的动态切换.基于MSH/WSN 肖特基结的可调谐肖特基二极管为替代传统的肖特基二极管提供了可能性.

图7 基于MSH/WSN 肖特基结的可调谐肖特基二极管的示意图Fig.7.Schematic diagram of a tunable Schottky diode based on MSH/WSN Schottky-junctions.

4 结论

本文采用第一性原理计算了外加电场和双轴应变对MSH/WSN 金属-半导体接触肖特基结势垒的调控作用.由二维金属材料和二维半导体材料WSN 构成肖特基结后,H 面接触模型MSH/WSN比S 面接触模型MHS/WSN 更稳定.两种肖特基结的能带均很大程度地保留了单层MSH 和WSN的能带特性,仅是两个单层材料能带的简单叠加.计算结果表明,外加电场和双轴应变均能有效调控MSH/WSN 肖特基结势垒.当正外加电场大于0.2 V/Å时,MSH/WSN 肖特基结可以实现p 型与n 型肖特基接触之间的转换;当负外加电场大于-0.2 V/Å时,MSH/WSN 肖特基结转化为欧姆接触.当双轴应变达到±8%时,可以使MSH/WSN肖特基结实现p 型与n 型肖特基接触之间的转换.本文为基于MSH/WSN 肖特基结的光电子器件提供了理论参考,同时揭示了WSN 材料在实际应用中的巨大潜能.