初拱变形对CRTSⅡ型轨道板上拱的影响研究

陈 醉,肖杰灵*,张雯皓,李 威,刘学毅

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031；2.西南交通大学土木工程学院,成都 610031)

CRTSⅡ型板式轨道(以下简称“Ⅱ型板”)是中国高速铁路的主型轨道之一，主要由钢轨、扣件、纵连式轨道板、砂浆层、底座板、附属结构等组成，轨道板通过纵向连接器及弹性混凝土砂浆组成的宽窄接缝结构实现连接，形成纵连式轨道[1-2]。受大规模施工作业、多变的下部基础和经时效应下的结构退化等因素限制，轨道板难以保持高度的均一性。板下CA砂浆调整层采用现浇水泥沥青混合料，对长期运营条件下的轨道板垂向约束能力有限；在温度、水及列车动荷载等多场耦合荷载共同作用下，极易形成板下脱空等病害，进而形成初始上拱(以下简称“初拱”)，在极端高温气候条件下进一步引发上拱位移，有系统性失稳破坏的潜在风险[3-4]。通过2013年对华东地区铺设Ⅱ型板的现场调研，受夏季高温天气影响，轨道板陆续出现胀板上拱现象，如图1所示。对于严重路段，轨道板出现14 mm上拱位移，用10 m弦测量，轨面出现左高低7 mm，右高低6.5 mm的情况。纵连式轨道的这一病害问题极大地威胁着高速行车的品质与安全，引起了广泛关注。

图1 现场轨道板上拱

针对纵向连续结构的失稳问题，学者们做了大量的工作。如Euler于1744年即提出压杆稳定性计算公式[5]；周敏等研究了简支梁桥上的Ⅱ型板的稳定性，认为不能把轨道结构当作理想Euler杆件，需考虑实际层间非线性约束[6]。对于Ⅱ型板在高温环境下的上拱问题，可从结构稳定性角度出发，通过能量变分原理研究其机理，该方法最早由Reissner提出[7]。我国在无缝线路领域提出的“等波长模型”与“不等波长模型”均以该原理为理论基础[8-10]。Ren、杨俊斌等借鉴“等波长模型”提出了Ⅱ型板的临界温度力计算公式，但忽略了轨道板初始上拱与实际上拱弦长不等的情况[11-12]。此外，学者们有关无缝线路失稳特性的研究对Ⅱ型板失稳分析亦具有重要的参考价值[13-16]。实践表明，弦长会伴随轨道板的上拱发生变化，其规律与轨道板初始缺陷、环境温度等因素相关。本文基于能量变分原理，研究初拱矢度、弦长等初始上拱特征值对轨道板上拱的影响，并通过数值拟合方法深入探讨上拱波长的演化机理，提出上拱矢度的关系表达式。

1 Ⅱ型板上拱理论分析

1.1 基本假设

根据Ⅱ型板的结构特点[1-2]，建立如下基本假设：

(1)将轨道板简化为均匀无限长平面梁模型，不考虑宽窄接缝伤损与假缝的作用，并忽略轨道结构的横向影响。

(2)现场调研表明，轨道板在高温环境下上拱矢度较小，故仅考虑结构处于弹性受力范围，不考虑轨道板受压破坏。

(3)钢轨自重与抗弯刚度、扣件系统对轨道板结构形变能影响较小，故忽略钢轨与扣件的约束作用，同时不考虑钢筋的作用。

(4)受温度、水及列车动荷载等多场耦合荷载共同影响，砂浆层与轨道板粘结作用大幅降低，故不考虑砂浆层对轨道板的粘结强度。

1.2 轨道板上拱曲线假定

在温度压力作用下，轨道板将在有初拱变形的区段产生上拱变形，由于Ⅱ型板为纵向连续结构，故变形后的轨道板在上拱段边界处曲率不发生突变。受下部基础的约束，设其上拱变形曲线y、初拱变形曲线y0分别为边界处无折角即一阶导数连续的半波二次正弦曲线，如图2所示。

图2 变形曲线假定

其中，l0、f0、l、f分别为轨道板初拱变形与上拱变形的弦长与矢度。根据图2，轨道板变形后的曲线

(1)

1.3 轨道板形变能

随着整体温升幅值增大，轨道板变形逐渐扩大，直至失稳屈曲的状态，其间轨道板累积总势能U主要由轨道板压缩形变能U1、弯曲形变能U2及轨道板重力势能U3组成。

(1)轨道板压缩变形能U1

在温度压力P作用下，轨道板发生轴向压缩变形Δl。在轨道板上拱过程中，温度压力P做负功，故压缩形变能

U1=-PΔl

(2)

根据上拱曲线的几何关系，Δl可表示为

(3)

联立式(1)-式(3)，压缩变形能U1可表示为

(4)

(2)轨道板弯曲形变能U2

轨道板在上拱变形过程中，结构内部会产生沿纵向分布的弯矩M(x)，假设轨道板为受弯梁，若抗弯刚度为EI，根据能量准则，忽略轨道板的弹性初始弯曲后，板中积蓄弯曲形变能U2可表示为

(5)

(3)轨道板重力势能U3

轨道板在发生上拱变形过程中需克服重力做功，若轨道板密度为ρ，横截面面积为A，则轨道板在上拱过程中积累的重力势能

(6)

1.4 轨道板上拱矢度

根据能量驻值原理，对U求f的偏导得

(7)

若轨道板混凝土线膨胀系数为α，板中整体温升幅值为ΔT，轨道板温度压力P可近似为

P=EαΔTA

(8)

假定l与l0比值为k，联立式(7)、式(8)，轨道板上拱矢度f可表示为

(9)

根据式(9)，上拱矢度f受f0、l0与l共同影响。当分母无限趋近0，f趋近无穷大，可认定系统失稳。取4EIπ4-π2l2EαΔTA=0，得到轨道板失稳临界温升

(10)

2 公式验证

式(9)表明，轨道板实际上拱弦长与初始变形弦长比值k未知。下面采用数值方法验证公式的准确性，建立如图3所示的力学模型。模型采用平面Euler梁单元模拟轨道板，对梁单元施加温升荷载模拟轨道板升温。为消除边界效应，在初始上拱段两端建立长度为100 m的水平延伸段。在轨道板两端施加与整体升温幅度等效的纵向力约束。轨道板与底座板之间的约束简化为具有单向压缩功能的非线性弹性约束，模拟砂浆层的弹性支承刚度，忽略其黏结拉力，力-位移关系曲线由CA砂浆弹性模量等效转换获得[6]，如图4所示(位移以弹簧受拉为正，受压为负)。

图3 力学模型图示

图4 砂浆层垂向力-位移参数曲线

模型主要计算参数如表1所示。

表1 主要计算参数

根据轨道板结构特性，假定轨道板初拱弦长分别为一块板长6.5 m、两块板长13 m，通过数值计算得实际上拱弦长，代入式(9)、式(10)计算，公式法与有限元法计算所得的上拱矢度f如图5所示，ΔTcr对比如图6所示。

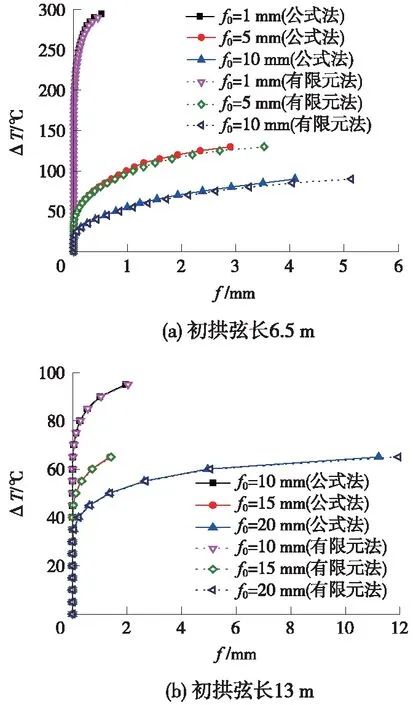
图5 上拱位移对比

图6 临界温升对比

结果表明，公式法与有限元法计算结果吻合较好，公式法所得结果稳定性略高。由于实际轨道板上拱过程中，温度压力与环境温度不是严格按照线性变化。式(9)、式(10)所得温度压力偏大，两端约束略强，故所得结果偏于稳定。当结构处于弹性变形阶段时，误差较小。现场调研结果表明，轨道板整体温升幅值不会超过60 ℃，其变形处于弹性范围内，故本文推导所得轨道板上拱矢度表达式可用于深入分析Ⅱ型板的垂向稳定性问题。

3 上拱弦长规律分析

根据式(9)，轨道板上拱弦长未知，而轨道板上拱矢度与上拱弦长密切相关，上拱弦长受板中温度压力及初拱矢度、弦长等因素影响。由于轨道板上拱问题具有高度非线性，常用的能量法难以得出上拱弦长的精确解，下面在式(9)的基础上，采用数值方法进一步分析上拱弦长变化规律。

3.1 上拱初始温升幅值

计算表明，在ΔT达到特定值之前，受重力场约束，板体不会产生垂向上拱。假定轨道板存在l0=6.5 m、f0=1 mm的初拱变形，理论上ΔT需达到约143 ℃时，轨道板才会发生进一步的垂向上拱，故矢度较小的初拱变形不会导致轨道板上拱。根据轨道板制造技术条件[17]，其初始平整度为±0.3 mm，小于1 mm，故施工和运营初期不会成为诱发系统垂向失稳的主要因素。定义轨道板开始产生上拱变形对应的整体温升幅值为上拱起始温升ΔT0，经计算，ΔT0随l0、f0的变化规律如图7所示。

图7 初始温升幅值变化规律

图7表明，ΔT0的取值与l0、f0密切相关，ΔT0与l0、f0分别呈正增长与负增长的关系，其变化规律可近似为指数函数与幂函数相乘的形式。经数值拟合，ΔT0与l0、f0的关系可表示为

(11)

结果表明，若初拱弦长较短，微量的温升幅值便能导致轨道板上拱，根据式(11)，若初拱矢度为1 mm，初拱弦长为0.5、1、1.5 m的轨道板对应起始温升幅值分别为0.9、3.6、7.9 ℃，即小于10 ℃的整体温升便能引发轨道板的上拱。故在实际施工与运营过程中，需关注板底局部脱空的情况，并及时采取措施，以防轨道板进一步的上拱。此外，当轨道板初拱弦长较长、初拱矢度较小时，上拱起始温升有明显增大趋势。因此，在高温环境下，对于轨道板底产生大面积脱空的情况，板体不易产生上拱位移。现场调研表明，在极端高温条件下，板中整体温升ΔTmax不会超过60 ℃。假定ΔTmax分别为40、50、60 ℃，不同初拱弦长的轨道板若保持图8所示的安全初拱矢度f1范围内，则板体不会产生垂向上拱。

图8 轨道板不同初拱弦长安全初始上拱幅值

3.2 上拱弦长取值

前述分析表明，ΔT大于ΔT0后，轨道板才会产生垂向的上拱，故与轨道板实际上拱变化规律相关的是上拱净温升幅值ΔTn，其中ΔTn与ΔT、ΔT0关系为

ΔTn=ΔT-ΔT0

(12)

受预制轨道板长影响，以其为弦长的初拱变形是最常见的初拱形态，故假定l0为6.5 m，经计算，l与f0、ΔTn的变化规律如图9所示。

图9 轨道板上拱弦长变化规律

图9表明，若l0保持不变，l随ΔTn、f0的增大而变长，其中l与ΔTn大致满足3次多项式关系。根据图9中的曲面形状，可判断l与ΔTn、f0的关系式中包含交叉项。假定上拱弦长满足l=f(ΔTn)×g(aΔTn+bf0)的多项式关系，经数值拟合，l与ΔTn、f0的关系可表示为

(13)

式中，系数ai与l0相关，其取值关系如表2所示。

表2 系数ai与初拱弦长关系表达式

联立式(9)、式(11)～式(13)，并结合表2计算所得系数ai，即可在已知板中整体温升幅值、轨道板初拱弦长、初拱矢度的条件下得到轨道板上拱矢度与上拱弦长。若上拱过程中轨道板不发生强度破坏，该算法可用于预测温度力作用下有初拱变形的Ⅱ型板在失稳屈曲前(即ΔT<ΔTcr)的上拱稳定特性。

3.3 上拱弦长与上拱矢度变化规律分析

(1)初拱弦长的影响

因Ⅱ型板纵连施工时间长、程序复杂，下部基础多变，成型后的轨道板系统会存在不同弦长的初拱变形。现场调研表明，运营阶段的Ⅱ型板离缝在1～14 mm的范围内，故假定初拱矢度为5 mm，联立式(9)、式(11)～式(13)得轨道板在不同温度环境下上拱弦长、矢度随初拱弦长的变化规律分别如图10、图11所示。

图10 不同初拱弦长轨道板上拱弦长

图11 不同初拱弦长轨道板最大上拱位移

结果表明，初拱弦长发生变化时，上拱弦长与上拱矢度有不同的峰值点，其中上拱弦长峰值点对应的初拱弦长比上拱矢度峰值点对应的初拱弦长略长。若初拱弦长超过峰值点对应长度，受重力场的约束作用，轨道板的上拱效应逐渐减弱。整体温升60 ℃条件下，初拱弦长为4.5 m时，轨道板上拱矢度达到最大值0.28 mm，此时轨道板上拱弦长为4.4 m；初拱弦长为6 m时，上拱弦长最长为4.6 m，而上拱矢度仅0.17 mm。初拱弦长为4.5、6 m时，对应上拱矢跨比(即上拱矢度与上拱弦长比值)分别为0.64 mm/m与0.37 mm/m。因此，整体温升60 ℃条件下，4.5 m的初拱弦长对行车安全影响最大。综合分析不同整体温升的情况，轨道板初拱矢度为5 mm时，弦长为2～6 m的初拱变形会产生明显的上拱矢跨比，现场应密切关注。

(2)初拱矢度的影响

轨道板受施工环境、流程等影响，会形成不同矢度的初拱变形。现场调研表明，板底贯穿离缝在纵向多为3～7 m的长度，故现假定以预制轨道板长6.5 m为初拱弦长。联立式(9)、式(11)～式(13)得轨道板上拱弦长、矢度随初拱矢度变化规律分别如图12、图13所示。

图12 不同初拱矢度轨道板上拱弦长

图13 不同初拱矢度轨道板最大上拱位移

结果表明，初拱矢度发生变化时，上拱弦长与矢度亦对应不同的峰值，其中上拱弦长峰值点对应的初拱矢度比上拱矢度峰值点对应的初拱矢度略短，初拱矢度超过峰值点对应幅值后，轨道板上拱则需要更大的温度压力。整体温升60 ℃条件下，若初拱矢度保持30 mm范围内，上拱矢度随初拱矢度幅值增大而增大；初拱矢度为23 mm时，轨道板上拱弦长达到最大值8.4 m。若初拱矢度不超过现场调研的最大值14 mm，轨道板上拱矢度与初拱矢度在不同温升环境下均保持正增长关系，其中初拱矢度小于5 mm时，轨道板在高温环境下几乎不会产生上拱位移。

(3)板中温升幅值的影响

现场调研表明轨道板最大温升幅值约60 ℃，为具体分析温度对轨道板上拱弦长与矢度影响规律，将板中温升的分析范围扩大至失稳屈曲状态下的临界温升。假定轨道板初拱弦长为6.5 m，在不同初拱矢度条件下，上拱弦长、矢度随板中温升幅值的变化规律分别如图14、图15所示。

图14 不同温升轨道板上拱弦长

图15 不同温升轨道板最大上拱位移

结果表明，产生上拱位移的轨道板，其上拱弦长随整体温升幅值大致呈反S形曲线规律变化。对于上拱初期，随着轨道板整体温升幅值的增大，上拱弦长开始突增；当上拱弦长接近初拱弦长时，上拱弦长的增长速率开始变缓；上拱弦长超过初始弦长后，其增长速率继续增大，直至系统失稳。图15表明，若整体升温幅度控制在20 ℃内，轨道板不会产生明显的上拱位移。故施工过程中宜控制轨道板纵连时的锁定温度，防止板内温升过高，避免极端高温对轨道板的稳定性产生不利影响。

3.4 轨道板上拱稳定性分析

由于国内目前对无砟轨道上拱限值尚未确定，参考无缝线路稳定性统一计算公式准则[12]，当f达到2 mm时，即可判定结构超出安全范围。假定ΔTmax分别为40、50、60 ℃，轨道板存在不同l0的初拱变形，若f0能小于图16中f0cr限制，即f不超过2 mm的限值，对行车安全不会造成影响。

图16 不同初拱弦长轨道板临界初拱矢度

图16表明，当初拱弦长保持在5～6 m时，轨道板稳定性最低，其中，初拱矢度分别为9.53、8.44、7.91 mm时，40、50、60 ℃的整体温升幅值便使轨道板上拱矢度达到2 mm的临界值。故在实际施工与运营过程中，应关注板底脱空长度5～6 m的伤损路段。

4 结论

(1)推导了CRTSⅡ型板上拱矢度的计算公式，经与数值方法的计算结果比较，二者偏差较小，可用于轨道板有初拱变形条件下的垂向稳定性分析。

(2)若初拱弦长小于1.5 m，幅值小于10 ℃的整体温升便能导致轨道板上拱；对于轨道板底产生大面积脱空的情况，板体不易产生上拱位移。

(3)不同的温升荷载作用，存在着不同的最不利弦长与矢度。若初拱矢度不超过5 mm，整体升温幅度控制在20 ℃内，轨道板在高温环境下不会产生上拱位移。轨道板初始上拱弦长为5～6 m时，最不易保持2 mm的上拱位移临界值。