快慢速列车共线运行的160 km/h级市域快线最小曲线半径研究

王仲林,易思蓉,王艺飞

(1.广州地铁设计研究院有限公司,广州 510010； 2.西南交通大学土木工程学院,成都 610031； 3.高速铁路线路工程教育部重点实验室,成都 610031)

随着我国城市规模、人口、经济的飞速发展，越来越多的城市发展趋势呈现出多中心的态势，“多核”、“高新区”、“副中心”成为城市发展的主要方向之一；城市主副中心、组团间的快速连接通道随之成为支撑城市多中心架构的重要一环。市域快线作为城市轨道交通线网体系中的组成部分，以服务城市内部组团为主要任务，意在实现城市各区域核心区之间的快速连接，区间长、速度快、开行对数高等特点，决定了其与传统地铁、国铁及城际铁路均有所不同[1-2]。目前，国内已开通2条120 km/h市域快线，分别为广州地铁3号线及深圳地铁11号线。对于速度高达160 km/h的市域快线线路技术条件，虽然在团体标准《市域铁路设计规范》中给出了相应的标准和参数[3]，但设计单位在实际工程应用过程中，尚缺乏系统的理论分析和方法指导[4]。

另一方面，随着我国区域经济的快速发展，新型城镇化建设步伐不断加快，人们居住、工作观念日渐转变，时速160 km左右、旅行时间1 h左右的城市圈/区域经济圈应运而生，时速160 km级城际快速轨道交通能很好地接驳城际铁路和城市轨道交通网络，满足城镇间时速140～160 km城市/市域轨道交通实现公交化运营的要求[5]。

最小曲线半径作为主要技术标准之一，对列车运行品质和工程建设投资具有重要影响，不同速度等级的轨道交通系统，均需制定与之匹配的最小曲线半径标准[6-11]。

本文综合采用安全度分析、旅客乘坐舒适度试验和车-线动力学仿真分析方法[12，14]，研究匹配快慢速共线运行160 km/h级市域快线系统特点的线路最小曲线半径标准。

1 最小曲线半径计算理论

满足旅客舒适度是轨道交通线路设计的基本要求。对于快慢速列车共线运行的轨道交通线路，设计还应保证在列车以不同速度运行条件下，轮轨磨耗均匀和内外轨受力均等，以保证轨道的稳定和行车平稳。基于限制未被平衡离心加速度原理选择曲线半径的方法，被国内外轨道交通系统广泛采用。

1.1 旅客列车最高行车速度要求的最小曲线半径

最小曲线半径应保证旅客列车以最高速度Vmax通过时，所感觉到的欠超高hq不超过允许值hqy，以保证旅客舒适度。满足旅客舒适条件的最小曲线半径Rmin为[15]

(1)

式中Vmax——旅客列车最高行车速度，km/h，通常取设计速度目标值；

hmax——最大超高值，mm；

hqy——欠超高允许值，mm。

1.2 快、慢速列车共线运行条件下的最小曲线半径

快、慢速列车共线运行城轨线路上，最小曲线半径的设置既要保证快速列车通过时，产生的未被平衡欠超高不超过允许值hqy，又要保证慢速列车通过时产生的未被平衡过超高不超过允许值hgy；因此，保证在快、慢速列车共线运行条件下行车安全、平顺和旅客舒适条件的最小曲线半径Rmin应按下式确定

(2)

式中Vmax——快速列车速度，km/h；

VDmin——慢速列车速度，km/h；

hgy——过超高允许值，mm。

快、慢速列车共线运行条件下的最小曲线半径Rmin，取式(1)、式(2)计算结果的最大者。

上述计算理论表明，轨道交通线路最小曲线半径的大小，取决于旅客列车最高速度、速度匹配模式、曲线外轨实设超高、未被平衡超高允许值等参数的合理取值。

本项目主要研究160 km/h速度级城市轨道交通快线的最小曲线半径计算理论和技术参数取值标准，考虑到城市轨道交通快线将来有发展为200km/h的条件，直接选择200、160、120 km/h和100 km/h四种速度作为研究参数。

2 曲线外轨实设超高允许值

轨道交通线路允许的最大超高值主要从两个方面考虑，一方面是从安全上考虑，即车辆在有超高的曲线上停车或低速通过时，如果从曲线外侧来风不会使车辆向内侧颠覆；另一方面是从舒适度上考虑，即旅客不会因车辆的倾斜而感到不舒适[16-21]。

2.1 安全条件所确定的最大超高允许值

车辆静态倾覆超高是车辆在无风静态时，处于临界倾覆状态的超高，是确定最大允许超高的依据。车辆静态倾覆超高可按下式计算

(3)

式中S——两轨头中心线之间的距离，mm，准轨铁路轮轨接触点中心距取1 500 mm；

n——安全系数，国内外经验证明，轮轨线路按安全系数取3所确定的最大超高值，能满足运营安全要求；

H——车体重心高度，mm；我国市域A型车、市域B型车、市域D型车、市域CRH型车的重心高度分别为1 695、1 895、1 650 mm和1 670 mm[21]，按此参数计算得到的最大允许超高分别为

按最不利包容原则，车辆静态倾覆条件限制的超高应不大于197 mm。

考虑到车辆弹簧装置横向变位、外侧风等因素会引起重心的移动，其影响约占静态计算值的12%[22]，则车辆静态倾覆条件所确定的最大超高允许值约为175 mm。

2.2 舒适条件所确定最大超高允许值

确定曲线最大超高还应考虑到当列车在曲线上停车时，旅客对处于倾斜车体里的舒适度反映，以及车辆处于倾斜状态下时机构的可靠性条件等。

列车在曲线上停车时，乘车舒适主要受外轨超高影响。据1978年10月铁科院进行车辆静载临界倾覆超高试验，当车辆停在试验线上，外轨超高达150 mm以上，旅客少部分人开始有不舒适感，当超高达200 mm左右时，一般可以忍受，超过250 mm时，大部分人站不稳，行走困难，头晕不适[21]。故按舒适条件最大超高不宜超过200 mm，此时车底倾斜角约为7.5°。

2.3 最大超高取值建议

综合安全条件与舒适条件的分析结果，并参考国内外研究与工程实践，本文建议我国快慢速组合模式下160 km/h速度级市域快线的最大允许超高值如表1所示。

表1 允许最大超高建议值 mm

2.4 推荐超高的动力学仿真分析

实设超高是线路中真实存在的超高，不因车辆速度等因素的变化而变化，实设超高设置合理与否，将直接关系到运行车辆的动力学性能；笔者所在课题组以曲线通过速度200/120 km/h的快车和慢车组合运行为例，基本线型组合为直线(100 m)+缓和曲线(340 m)+圆曲线(200 m)+缓和曲线(340 m)+直线(100 m)，实设超高取30～170 mm，分析不同曲线半径下的实设超高对车-线动力学性能的影响[23]，图1～图6展示了快慢车共线市域快线在不同平面圆曲线半径下的实设超高对动车组列车的动力学性能的影响。

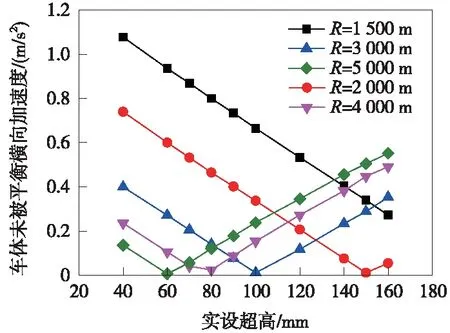
图1 车体横向加速度与实设超高的关系

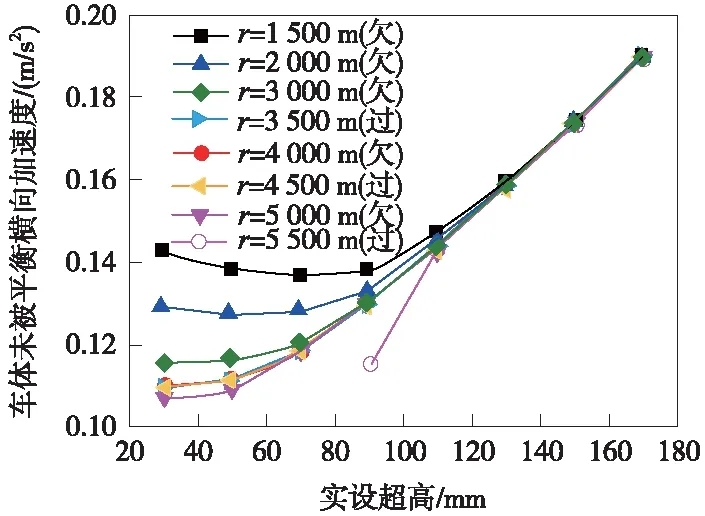
图2 车体垂向加速度与实设超高的关系

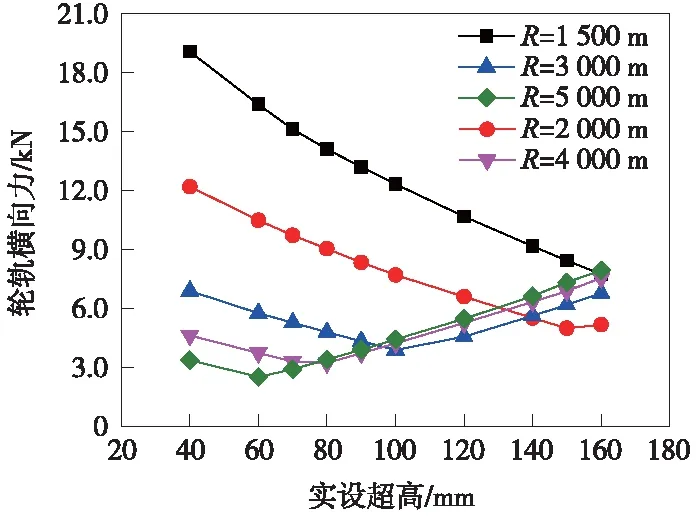
图3 轮轨横向力与实设超高的关系

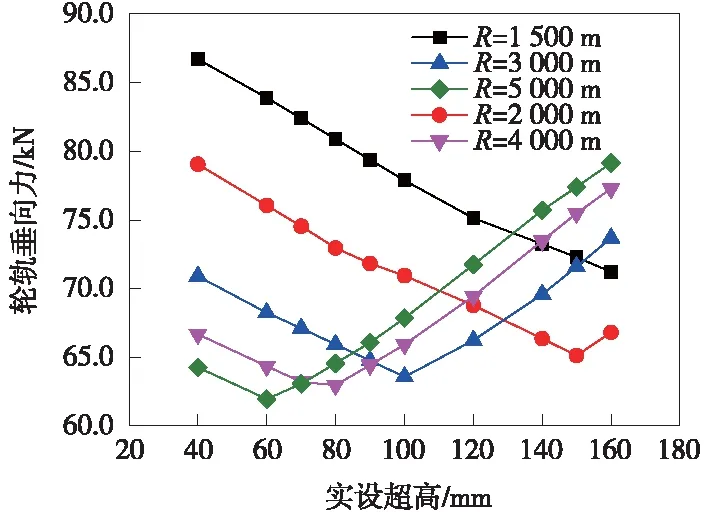
图4 轮轨垂向力与实设超高的关系

图5 轮重减载率与实设超高的关系

图6 脱轨系数与实设超高的关系

分析图1～图6的规律可得到以下结论。

(1)从指标度量值看，在40～160 mm的实设超高范围内，各项动力特性指标(车体横向加速度、车体垂向加速度、轮轨横向力、轮轨垂向力、轮重减灾率、脱轨系数)均小于各自的限值，满足行车平稳性、安全性的要求。

(2)总体来看，各项动力学性能指标在均衡超高附近达到最小值；当实设超高小于均衡超高时，动力学性能指标值随实设超高h的增大而减小；其变化规律基本成AX+B线性关系；在相同超高下，动力学性能指标随半径增大而减小，各半径下的动力学性能指标与超高的关系曲线近似平行。

(3)仿真计算结果还证明，未被平衡超高的形式，影响着车-线动力学性能随实设超高的变化规律。在欠超高工况下，车辆运行性能指标随实设超高h的增大而减小；过超高状态下，车辆运行性能指标随实设超高h的增大而增加；这表明，曲线实设超高不宜大于曲线均衡超高。

(4)由图2可知，在所研究的实设超高范围内，动车组的车体垂向加速度变化非常小，动车组的车体垂向加速度均在0.1～0.2 m/s2，在欠过超高状态下，动车组列车的车体垂向加速度均随实设超高缓慢增加。但均小于各自的限值，满足垂向平稳性的要求；曲线超高的大小对车辆垂向振动加速度的影响不明显。

3 欠超高允许值

在快慢速共线运行的线路上，实设超高通常按平均速度设置。当列车以高于平均速度的速度通过曲线时，会产生未被平衡的离心加速度；未被平衡的离心加速度可以理解为由于外轨超高不足所产生，亦即会感觉存在欠超高。为了保证列车运行安全和旅客舒适性，列车通过时产生的欠超高不能超过一定的限制值。

曲线欠超高允许值的确定，既要考虑列车运行的安全、轨道的横向稳定，又要考虑旅客乘坐的舒适度。世界各国铁路由于采用的机车车辆、运输模式、轨道结构和列车最高运行速度的不同，所规定的允许欠超高值也有所不同。通常认为，速度越高，安全性和舒适性的储备量应当越高。欠超高允许值hqy可通过旅客乘坐舒适度试验、动力学仿真分析和工程实践类比等方法确定。

3.1 旅客乘坐舒适度试验

为了探明旅客舒适性与线路参数之间的相互作用机理，西南交通大学课题组于2009年11月～2010年3月期间在广深线、遂渝线城际旅客列车上进行了旅客乘坐舒适度现场试验研究[13]。舒适度试验可知欠超高、未被平衡离心加速度和旅客舒适度之间的关系如表2所示。

表2 欠超高、离心加速度和旅客舒适度间的关系

3.2 安全度确定的欠超高允许值

考虑快速动车组以最高速度通过曲线时，所产生的未被平衡欠超高最大值不致使列车向外倾覆。如车辆向外侧颠覆的安全系数取4(危险率为25%)，即合力作用点在轨距的1/8以内，则最大欠超高允许值为[13]

(4)

市域CRH型车体的重心高度按1 670 mm计，相应的欠超高最大值为

确定允许侧向未被平衡离心加速度标准，还应考虑高速行车的侧向风力作用、侧向振动加速度和高速会车时的侧向力作用的影响。据研究，在最不利情况下，这些侧向作用力的影响和离心加速度引起倾覆一起对轨道面设置超高引起的稳态倾覆起抵消作用。以未考虑这些因素的侧向稳态欠超高标准作为设计限制值，是偏于安全的。

3.3 车-线动力学仿真分析及欠超高计算模型

为了研究轨道实际状态下曲线技术条件对车辆系统运行性能的影响规律，按照轨道随机不平顺数值模拟方法，对德国低干扰谱、高干扰谱进行数值模拟，得到各项车体动力特性值与欠超高的关系[23]；其中，车体横向加速度与欠超高的关系如图7所示。

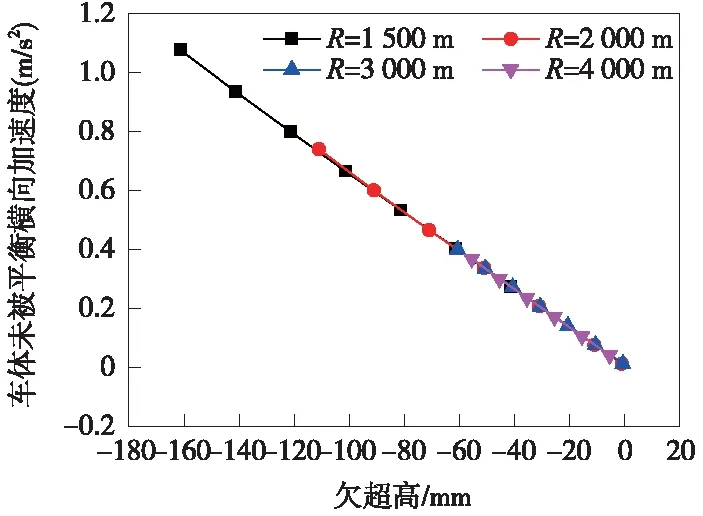
图7 车体横向加速度与欠超高的关系

仿真计算结果表明，快速列车通过曲线时的动力学特性与欠超高之间有以下相互作用规律。

(1)动车组列车的车体垂向加速度、轮轨横向力、轮轨垂向力、轮重减载率、脱轨系数，在所研究曲线半径和欠超高范围内均远小于限值，对行车安全性和舒适度不起控制作用。

(2)列车通过曲线时的动力性能，主要受未被平衡的离心加速度影响。由图7可知，同一曲线半径下，动车组的车体横向加速度随欠超高的增大而增大；欠超高在120 mm附近时，不同曲线半径下的车体横向振动加速度达0.8 m/s2，动车组横向加速度在欠超高约为140 mm时,达到旅客舒适所要求的限值1 m/s2。欠超高相同时，曲线半径越小，车体横向加速度越大，呈强线性关系；综合各工况的仿真计算数据，可得欠超高与车体横向加速度之间的关系模型如表3所示。

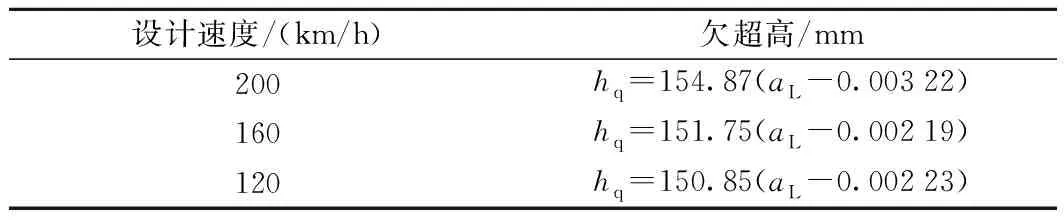
表3 欠超高值与车体横向加速度关系模型

3.4 欠超高允许值取值建议

综合国内外相关研究可知，欠超高允许值的决定因素是列车行车舒适条件。当列车通过平曲线时，旅客对车体横向加速度(aL)的反映状况如下：

当aL<0.4 m/s2，旅客对未被平衡的离心加速度无明显感觉；

当aL=0.5 m/s2，旅客能觉察到未被平衡的离心加速度，但无不舒服的感觉；

当aL<0.75 m/s2，一般旅客能长时间承受这种未被平衡的离心加速度；

当aL=1.0 m/s2，一般旅客能承受不频繁的这种未被平衡的离心加速度；

由表3关系模型，可得车体横向加速度与欠超高的对应关系见表4。

总之，在实施“微型探究”教学中，教师要善于在知识形成的“关键点”，在运用数学思想方法解决问题策略的“关节点”，在学生思维的“最近发展区”内，提出恰当的、具有思考价值的问题串，引发学生的思考与探索，启迪学生思维的深层参与，促进学生理解数学，高效学习，实现数学意识和数学核心素养不断得以提升！

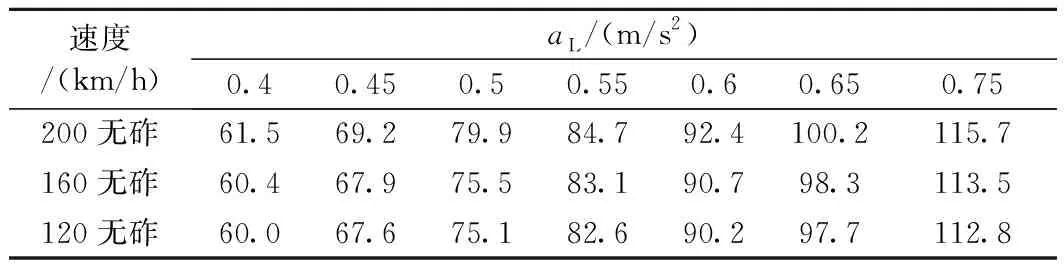
表4 不同车体横向加速度时的欠超高对应值 mm

根据表4数据，建议欠超高允许值取为：良好60 mm(0.4 m/s2)，一般75 mm(0.5 m/s2)，困难90 mm(0.6 m/s2)。

4 过超高允许值

在快、慢速混行的市域快线上，实设超高按平均速度设置。当列车以低于平均速度通过曲线时，则会产生未被平衡的向心加速度。未被平衡的向心加速度可以理解为由于外轨超高过大所产生。影响过超高的因素同样是，保证行车安全、旅客舒适、经济合理3个条件。受车辆运行安全、乘坐舒适度要求的过超高值的确定，与欠超高值确定原理基本相同。区别仅在于后者是车辆向曲线外侧倾斜，而前者是车辆向曲线内侧倾斜。

4.1 舒适度试验研究结果

根据课题组在遂渝线城际旅客列车上进行的旅客乘坐舒适度现场试验研究[13]可知，对于选定的曲线半径为1 600～4 000 m曲线，快速列车以100～120 km/h速度通过时，列车产生过超高hg的变化范围在5～20 mm，旅客无感觉的概率随过超高的增大而变小，轻微感觉，明显感觉的概率随过超高增大而变大；旅客无强烈感觉反映。曲线半径大于1 600 m的曲线，大部分旅客的感觉在轻微感觉之内。遂渝线的试验结果表明，列车通过曲线时，过超高状态下的舒适度感觉与欠超高状态下的感觉相当。列车通过无砟轨道地段旅客的舒适度感觉总体上比有砟轨道地段的舒适度感觉好。

4.2 车-线动力学仿真分析

对于快慢速共线市域快线而言，实设超高按平均速度设置，当慢速列车通过时，将产生过超高，影响旅客舒适度。通过动力学仿真分析，可发现车-线动力学特性值与过超高的变化规律[23]；其中时速200/120 km的快速动车组和慢速列车单元的车体横向加速度与过超高的关系如图8所示。

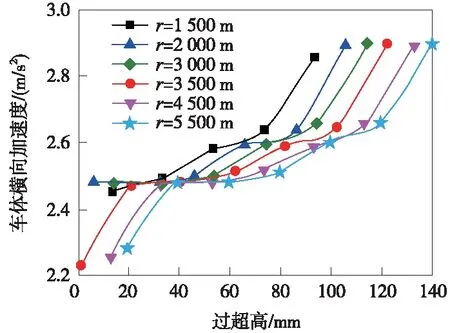
图8 车体横向加速度与过超高的关系

由仿真计算结果可知：

(1)慢速列车的车体垂向加速度、轮轨横向力、轮轨垂向力、轮重减载率、脱轨系数均小于限值，对行车安全性不起控制作用；

(2)由图8可知，同一曲线半径下，慢速列车的车体横向加速度随过超高的增大而增大，慢速列车的横向加速度在过超高状态均未超过其限值，过超高80 mm以下时，车体横向加速度均小于0.8 m/s2。

4.3 过超高允许值取值建议

上述建议标准小于国外160～200 km/h铁路的实际过超高值[24]，相比《市域快速轨道交通设计规范》增加了良好档[21]。

5 最小曲线半径标准研究

5.1 最小曲线半径标准推荐值

快、慢速列车共线运行的市域快线按速度120/160 km/h、100/160 km/h等运输组织模式进行计算，基础设施考虑预留200 km/h速度发展条件，速度匹配模式为：120/200 km/h、160/200 km/h。

根据本文第2、3、4节研究结果，最大超高取150 mm;欠超高取良好60 mm，一般75 mm，个别90 mm；过超高取良好50 mm，一般70 mm，个别90 mm。按公式(1)、式(2)计算各种运输模式下的最小曲线半径。

单一快速列车运行的市域快轨线路最小曲线半径计算值及推荐值见表5。快、慢速列车共线运行的市域快轨线路最小曲线半径计算值及推荐值见表6。

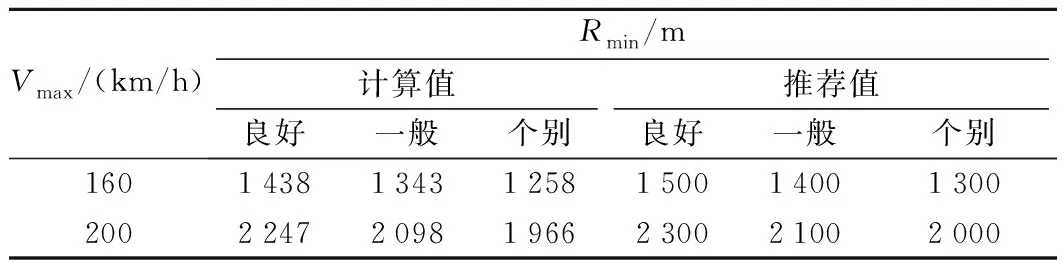
表5 单一快速列车运行线路最小圆曲线半径Rmin

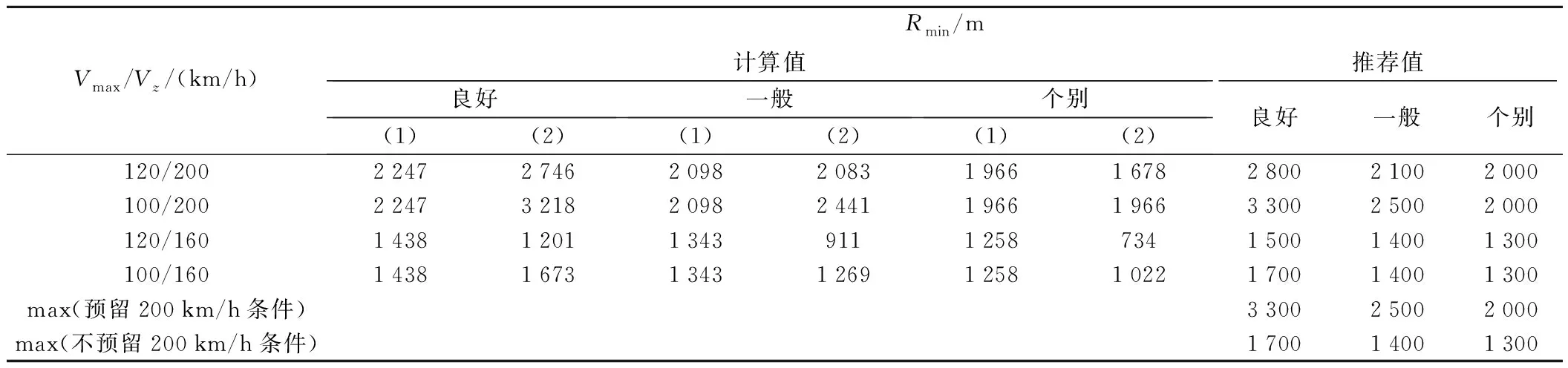
表6 快、慢速共线运行线路最小圆曲线半径Rmin

注:(1)和(2)分别代表按式(1)和式(4)计算的结果。

表6计算结果表明：对于快慢速列车共线运行的城轨系统，大部分工况下，确定最小曲线半径的控制因素是同时保证快速列车通过时欠超高不超限，慢速列车通过时过超高不超限。按旅客舒适度确定的最小曲线半径，也能满足快速列车通过时的舒适度要求。

5.2 对最小曲线半径推荐值的评价

(1)动力学仿真分析

为了评价推荐标准的安全性和舒适性，用所建立的车-线动力学模型进行仿真计算[23]。计算结果表明，当半径大于1 500 m后，轮轨作用力、脱轨系数、轮重减载率均远小于限制值，客车轮轴力仿真计算结果在规定范围之内；可见，推荐的最小曲线半径能够通过安全性评估。

当半径为1 500 m时，仿真计算所得不同欠超高下的车体横向加速度如表7所示。

表7结果表明，当欠超高小于80 mm时，旅客舒适性能满足一般条件的要求；实际设计中，采用最小曲线半径值的曲线实设超高不宜小于60 mm。

表7 欠超高与车体横向加速度的关系

由此可见，列车以160 km/h的速度通过1 500 m曲线半径时，各项安全性指标有很大余量，舒适性指标满足一般条件。

(2)工程合理性评价

与国内外相关工程和规范对比可知，本文推荐的最小曲线半径标准建议值高于国外160 km/h和200 km/h的最小曲线半径标准[24]，小于我国《新建时速200公里客货共线铁路设计暂行规定》[25]、《铁路线路设计规范》[26]的取值，高于《新建时速200～250 km客运专线铁路设计暂行规定》[27]、《市域快速轨道交通设计规范》[3]、《城际铁路设计规范》[21，28]等客运专线的标准，与《高速铁路设计规范》[29]的相应标准值相当。

综上分析可知，本文综合考虑快、慢速旅客列车共线运行，且考虑旅客列车对欠超高和过超高的感觉达到同等舒适度，推荐的最小曲线半径值是合理的。