网络搜索模型在铁路选线方案优化辅助决策中的应用

张振峰,姚令侃,2,3,夏 烈,张孟帅

(1.西南交通大学土木工程学院,成都 610031； 2.高速铁路线路工程教育部重点实验室,成都 610031； 3.陆地交通地质灾害防治技术国家工程实验室,成都 610031； 4.中铁二院工程集团有限责任公司,成都 610031)

铁路建设是一项牵涉面广，影响因素多，技术层次高的复杂系统工程，可行性研究阶段所确定的铁路线路方案的优劣直接影响项目的经济和社会效益。

可行性研究阶段的定线工作内容是“从面到带”，即在1∶5万～1∶10万的地形图上，根据铁路规划的要求，在线路起讫点间的大面积范围内找出一切可能方案，经过概略评比后，提选出进一步比选的方案加以评价[1]。

铁路选线设计中，直接连接起讫点的方案称为贯通方案，在起终点位置间会设计出众多具有拓扑关系的局部比选方案。在传统选线设计模式中，当可行方案网络复杂时，一般是先分段选出局部最优方案，再将局部最优方案组合形成贯通方案。这样的做法可能存在的问题是，早期在某一段比选中丢失有比较价值的方案，在形成贯通方案时就不再考虑，这样有可能漏掉局部不利，而从全局来看有利的方案，所以必须增加对方案集的统筹考察。但干线铁路往往长达上千公里，各种局部方案的组合可能形成数量众多的贯通方案，如川藏铁路初期研究阶段全部局部比选方案的组合形成的贯通方案就多达555个，已构成复杂网络问题[2]，显然仍靠人工作业从事全部考察环节的工作量太大，有必要发展相应的自动化方法解决该问题。

图论是研究工程管理、计算机科学、系统工程等许多领域重要的工具。现实中很多问题，如交通网络、运输安排等，都可以转化为图论问题，然后用图论算法来解决[3]。例如：康志瑜[4]通过改进Dijkstra算法，在电子地图环境下实现了道路网络中任意两点间路径搜索与显示；李引珍[5]提出一种计算货物运输路径及里程的数学模型，可快速计算货物里程并绘制路径图；陈箫枫[6]通过改进最短路径算法，提出更适合公交查询的算法及其系统实现。在道路线路设计方面，余为波[7]将图论相关理论应用于舰艇通道路线优化设计，并对通道设计相关问题深化总结；李军[8]提出基于Dijkstra算法的一种最低风险线路方案搜索算法，实现了对高速公路风险水平最优方案的自动搜索。以上研究侧重寻求网络中两定点间的最短路径。

本文重点是研究如何利用网络搜索模型为铁路选线方案优化提供辅助决策信息。首先介绍了图论概念及相关原理；然后定义了铁路可行方案网络的数学描述方式；最后以川藏铁路选线设计为例，论述了网络搜索模型在确定推荐方案在可行方案集中的排序、分析存在较大优化空间的区段、甄别对铁路线路方案起控制作用的影响因素等方面的应用。

1 铁路可行方案网络搜索模型

1.1 图论及其相关概念

所谓图是指数学表达(V,E,φ)，V为非空有限集合，E是在V上的二元关系集，φ是E到V×V的函数。如果φ是元素的有序对集合，则称(V，E，φ)为有向图，记为D=(V，E，φ)。若φ是元素的无序对集合，则称(V,E,φ)为无向图，记为G=(V,E,φ)。V中的每一个元素vi(i=1,2,…,n))称为该图的一个顶点或节点；E中的每一个元素ak(即V中某两个元素vi，vj的有序对)记为ak=(vi,vj)，或被称为该图的一条从vi到vj的弧[9]。

除了弧的方向之外，如果对弧赋予了实际含义和权值，即给定有向图D=(V,E,φ)，对D中的每条弧α赋予一个实数w(a)，称为弧a的权。赋权的有向图称为网络图，记为N=(V,E,φ,w)。

1.2 铁路可行方案网络模型

铁路可行方案网络可看作包含某种二元关系的系统，所以可以采用图论中“图”来表示其网络结构，两者对应关系为：局部比选方案的起点、终点当作网络图中的节点，将两节点之间铁路线路表示成节点的弧，弧的权则用铁路的距离、费用、风险等指标量化来表示。当确定了节点、弧和权值以后，铁路网被抽象成一个赋权有向图，利用图论算法可快速求解图中任意两点间所有路径及其权值和，通过对结果深化拓展可以为优化设计提供决策信息。

2 方案评价体系

2.1 弧权评价指标

铁路选线设计方案评价指标较多，考虑的侧重点不同，选取相应的评价指标也有所不同。一般从影响线路走向方案的社会政治经济意义、工程数量、工程风险防范及防灾能力、施工及运营条件等4个方面考虑选取弧权指标，结果如表1所示，它包括12个二级指标，可针对不同选线方案实例作相应调整[10]。

表1 弧权指标体系

2.2 数据标准化

不同评价指标往往具有不同的量纲和量纲单位，为了消除由此带来的不可公度性，还应将各评价指标作标准化处理。而网络图中所有弧段分别求出权后，下一步方案评定需要求出任意两节点间弧段权值的和，所以评价指标应满足单调性。

表1中指标类型一般分为效益型和成本型：如工程数量、不良地质条件为成本型指标，属性值越小越好；而社会政治经济意义属于效益型指标，属性值越大越好，所以在标准化处理时必须将指标趋同化。

对于成本型指标

(1)

对于效益型指标

(2)

有向网络图弧段权值fa可用下式求出

式中wi——第i个评价指标的权重；

ui——第i个评价指标的值；

n——评价指标个数。

2.3 方案优劣评价标准

因为决策方案要实现的结果往往是多目标的，而多个目标之间有时又是互相矛盾的，所以决策者就很难以一个统一的评价准则对各个方案的优劣进行排序。本文的评价重点关注两类方案：(1)在反映决策者偏好的某个权重下排序第一的方案；(2)在不同权重分配方式的评价体系中，排序均靠前的方案，这样的方案各项指标比较平衡，认为是较为稳健的方案。

3 川藏铁路线路方案优化辅助决策应用案例

3.1 建立模型

现以川藏铁路康定至林芝段选线设计为例进行分析。首先将康定至林芝研究过的方案集抽象成网络图，并标注相关节点名称，如图1所示。

图1 线路方案网络示意

然后，根据川藏铁路“高海拔、大高差、复杂艰险山区”的地形特点和复杂工程地质特点等因素，决定选取以下指标体现表1所示4个方面[11]。

(1)在前期规划研究阶段，简单地可选取铁路线路长度作为体现工程数量的指标。具体做法为：根据线路平面图，确定网络图中弧段对应的长度。

(2)影响川藏铁路的灾害类型较多，从举例角度，暂取地震风险作为体现工程安全的指标。具体做法为：将线路可行方案绘于第五代国家地震动峰值加速度区划图上(图2)，以线路经过不同区域的实际长度与地震峰值加速度乘积之和来衡量弧段地震风险。

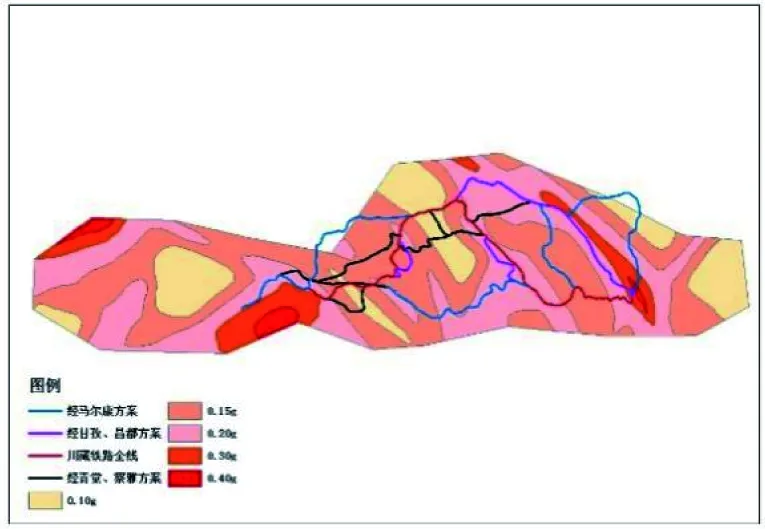
图2 地震动峰值加速度区化

(3)川藏铁路沿线居民点稀人少，公路交通网络稀疏，大型居民点大多沿公路干线(国道、省道)分布。新建铁路靠近既有公路干线既可减少建设期的临时工程，还可为运营期的职工生活提供便利；此外，铁路靠近既有公路干线也有利于吸引客货流和促进地方发展。鉴此，特选取铁路利用既有公路干线的线路长度为反映施工及运营条件和社会政治经济意义方面的指标。具体做法为：将线路绘制在国家公路网规划—普通国道网布局示意图上，然后计算网络图中各弧段10 km范围内利用公路干线的线路长度占弧段长度的比例。

在数据标准化处理时，(1)、(2)均可按成本型指标处理(式(1))，(3)按效益型指标计算(式(2))。

3.2 选线辅助决策

以上工作完成了对川藏铁路前期研究阶段方案集网络的数学描述，建立了搜索模型。现利用该模型开展以下研究。

3.2.1 线路走向方案的讨论

(1)在康定—林芝线路走向选择中阶段性地倾向于经理塘、昌都的方案，节点表示为1→2→6→8→9→10→11→13→14→15→16→17→18→19→20→22→23→24(倾向方案)。

在本文评价体系下，评价倾向方案在所有贯通方案中的优劣，采用不同权重反映决策者偏好，分别求出排序。权重分配方式见表2，方案排序结果见表3。

表2 弧段评价指标权重

表3 康定至林芝线路推荐方案排序

从表3可看出，倾向方案在不同权重的评价体系下，排序均属于前15%，认为是属于稳定方案类，即能较好地满足各项指标。

(2)选线设计中，有些影响因素主观性很强，比如，铁路必经城市或其他控制点的确定，就要兼顾国家、地方和铁路的利用，寻求合理的决策，但控制点的变化常会在很大程度上影响线路方案的走向。在本案例中，鉴于昌都市的特殊地理位置及其在康巴藏区的核心地位，昌都可能成为控制点；此外，根据铁路路网规划，八宿宜选为川藏铁路与滇藏铁路的接轨点，所以八宿成为铁路部门的控制点。

现利用网络搜索模型分析控制点作为强制约束条件时对线路的影响，具体做法为：在指标权重取平权的分配方式下，对555种可行方案进行排序，查找经两个控制点方案第一次出现的序号。结果为：第一次出现的经过昌都的方案排序第26(属前5%的方案)；第一次出现的经过八宿的方案排序为第1。说明，若以昌都作为控制点时，对方案优化格局有一定影响，但影响不大；而铁路内部将八宿作为控制点，则对线路方案优化无影响。

3.2.2 优化余地较大区段的确定

在讨论过线路走向方案后，下一步希望知道哪些是优化余地较大的区段。现以昌都为分界点，将线路分为康定—昌都、昌都—林芝两个区段，在平权下求出所有方案路径权值和。

康定—昌都，可行方案一共28种，将每种方案按照路径权值和排序大小绘于图3中。

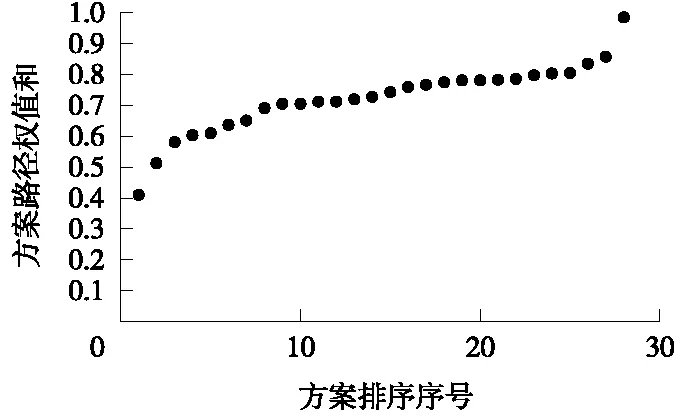
图3 康定—昌都各方案路径权值和示意

昌都—林芝，可行方案一共16种，绘图做法同康定—昌都区段，结果见图4。

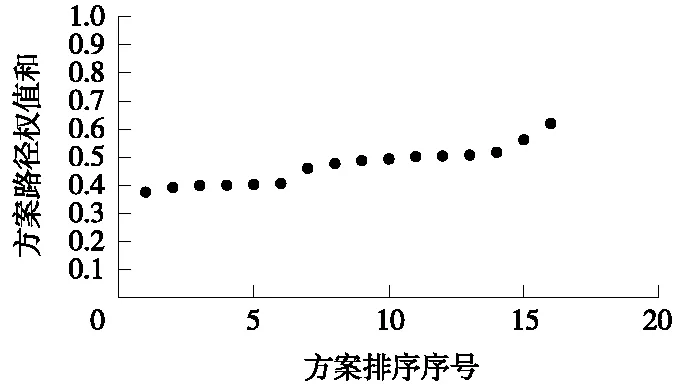
图4 昌都—林芝各方案路径权值和示意

计算以上2个区段方案数据的离散性，结果见表4。

表4 两区段方案数据离散性比较

由图3、图4及表4可看出，康定—昌都区段各方案路径权值和差距较大(标准差达0.112 7)，特别是排序为前三的方案、排序为后三的方案路径权值和变化趋势更为明显；而昌都—林芝区段各方案权值和差距不大(标准差为0.068 9)，特别是排序为第1至排序为第6的方案路径权值和接近。说明，昌都—林芝区段方案优化空间有限，在后续工作中，应将康定—昌都区段作为下一步优化的重点。

3.2.3 康定—昌都区段方案优化的研究

根据上文分析结果，康定—昌都区段为进一步比选的重点。现通过变化权重的分配方式，求出该区段所有方案的排序，不同权重下排序最优方案见表5。

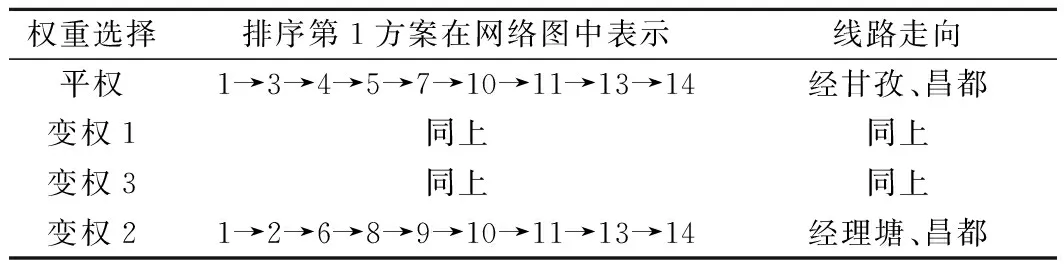
表5 康定—昌都区段排序最优方案

从表5可看出，按4种变化权重的评选方式，排序第1的集中在两个方案。即经甘孜、昌都的方案在平权(且由图3可见优势明显)、变权1、变权3的评价方式下均排序第1，在变权2(地震指标权重0.6)下排序为4/28；反之，经理塘、昌都方案仅在变权2下排序第1，其余权重下排序均不如前者。这就提示我们，对经甘孜、昌都的方案，若能在地震指标方面得到改善，就有可能成为最优方案，这样指明了康定—昌都区段方案优化的重点。

经甘孜、昌都的方案在康定至甘孜段，由于大段落线路与鲜水河断裂带平行，约有200 km位于0.3g地震烈度区，这是该方案在变权2评价方式时指标劣化的主要原因。深入分析可知，鲜水河断裂带由于走滑断裂特殊机制，其北西段交替出现了盆地和隆起山相间的地形。主要盆地有朱倭盆地、道孚盆地、虾拉沱盆地等，在纵断面上，这些盆地基本在同一高程面上，炉霍、道孚两县间的直线的自然坡降仅为4.5‰的缓坡地段，线路通过这些盆地时，有较开阔的地形可绕避平面障碍物；而在盆地间的隆起丘陵区，高程障碍也不大，可望以短隧、低桥方案穿越。因此，沿鲜水河断裂带的线路工程具有采用简易工程(造价低、震后易于修复)减轻地震灾害风险的条件[12-15]。综上，建议后期继续加强对经甘孜、昌都方案的深化研究，从而能够对地震风险可能降低的程度进行定量分析，然后基于风险评估结论对两个代表性方案进行比选，确定最优方案[16]。

4 结语

(1)本文提取抽象的铁路方案网络图，结合弧权评价指标体系，建立网络搜索模型，得以快速计算不同权重的方案网络权值和及其排序，有利于分析在不同偏好下各方案可能的后果和影响，为选线设计提供辅助决策信息[17]。该模型在川藏铁路方案优化辅助决策中应用的案例表明，当铁路可行方案网络复杂性高时，该方法可提高对大数据分析的自动化程度。

(2)虽然本文选取的三项弧段赋权指标的确是川藏铁路选线设计时应考虑的关键因素，但案例研究主要是为了说明网络搜索模型如何应用，其他方面有所简化。实际上每条铁路弧权指标体系都应根据具体情况选取，而且随着选线设计阶段的深入，指标体系也宜逐步细化。