增湿条件下膨胀土边坡稳定性影响因素有限元分析

张 硕,蒋良潍,罗 强,李傲赢,司光武

(1.高速铁路线路工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

膨胀土是主要成分为亲水性黏土矿物的高塑性黏土[1]，具有颗粒高分散性、对环境湿热变化敏感的特点。膨胀土边坡失稳破坏是岩土工程所遇到的难题之一，降水入渗条件下，土体增湿自重增加、抗剪强度降低以及产生膨胀作用，影响膨胀土边坡稳定性。这三项重要因素的综合作用，增加了膨胀土边坡稳定性分析的难度。

膨胀土边坡的稳定性分析计算，主要分为传统极限平衡法和有限元数值模拟法两类。殷宗泽等[2]提出以条分法为基础，近似反映裂隙对膨胀土边坡影响的分析方法，指出裂隙程度如何，对抗剪强度影响很大。卫军等[3]考虑土体强度衰减特性，通过条分法分析了膨胀土边坡的稳定性。条分法基于刚体极限平衡原理，需要假定滑面形状、位置和条间力，利用有限元方法则可以考虑土体变形与应力调整，实现滑面的自动搜索。但如何合理模拟膨胀作用成为有限元分析中的难题。

有限元分析中，一般通过温度场比拟湿度场来实现土体增湿膨胀的模拟。缪协兴等[4]首次提出了湿度场与温度场等效理论，通过编制的湿度场有限元程序，分析了膨胀岩各向同性膨胀及软化问题；刘静德等[5]通过定义温度场，将各向同性膨胀力引入到通用有限元软件中，以模拟膨胀土边坡降雨破坏过程。但是，由于土体结构的各向异性，膨胀土普遍具有各向异性膨胀的特点，张颖均[6]通过三向胀缩仪研究了裂土的各向异性膨胀性质，指出膨胀土垂直膨胀力大于水平膨胀力，因此边坡稳定性有限元分析中采用各向同性膨胀假设仍不尽合理。

秦禄生、郑建龙等[7]考虑水平和竖向最大膨胀力不同，将膨胀力作为体力引入到有限元软件中，模拟了膨胀土路基边坡的雨季失稳破坏，但关于膨胀差异性大小对边坡稳定性的影响未开展计算。由于增湿后土体增重、强度衰减和产生膨胀作用这三项因素的作用效应相互关联，已有工作多侧重于研究其中的一或两项，鲜有针对差异膨胀性条件，通过考虑三项因素综合作用的有限元分析方法，探讨膨胀土边坡稳定性和影响因素的主次关系。

论文基于热膨胀比拟增湿膨胀原理，推导描述土体差异膨胀的应力-应变方程，导入ABAQUS有限元强度折减法，开展膨胀土边坡算例的稳定性研究，并通过正交试验极差分析，讨论三因素对膨胀土边坡稳定性影响的作用效应及敏感性。

1 增湿差异膨胀的热胀比拟模型

膨胀土边坡雨季吸水，在变形约束下会导致膨胀力，引起边坡变形及应力调整，对稳定性产生不利影响。基于温度和湿度变化产生应变相等的温度与湿度线膨胀系数等效关系理论[5]，进一步建立柱坐标下各向异性增湿膨胀应力-应变方程，以无荷膨胀率土工试验的对应ABAQUS有限元模型进行验证。

1.1 增湿膨胀与热膨胀的应变等效原则

针对膨胀土吸水膨胀，已有研究建立了一些膨胀力或膨胀变形的计算公式。龙科军[8]假定有荷膨胀量与含水率呈线性变化关系，给出了含水率变化下膨胀土体积增量计算式；孙即超[9]根据弹性力学原理，基于膨胀变形与施加膨胀力的等价理论，给出了各向同性膨胀力的计算公式。

因此，以温度和含水率变化产生的应变相等，得到温度和湿度的线膨胀系数关系，进而引入到有限元，通过热膨胀等效模型模拟增湿膨胀的过程。热弹性体在温度增量ΔT下的应力应变方程为[10]

(1)

(i，j，k，l=x，y，z或1，2，3)

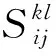
基于温度场等效湿度场的线性假设[5]，温度增量(℃)下产生的应变增量Δε为

Δε=αΔT

(2)

式中，α为温度线性膨胀系数，℃-1。

湿度增量产生的应变增量Δε可表示为线性方程[4-5]

Δε=βΔw

(3)

式中，β为湿度线性膨胀系数；Δw为含水率增量，%。

温度膨胀变形和增湿膨胀变形等效的关键是膨胀系数之间的关系，温度场常用的单位为℃，而表征含水率取%为基本单位，在应变相等的条件下，α、β值分别与之相匹配。因此，对于式(2)、式(3)，含水率每变化1%与温度每变化1 ℃的应变等效，可得

α=0.01β

(4)

根据无荷膨胀率试验测得膨胀土湿度线膨胀系数β，即可由式(4)求得等效温度场的温度线膨胀系数α。若温度单位取℉，温度线膨胀系数单位为1/℉，则有含水率每变化1%与温度每变化1.8 ℉应变等效。

1.2 柱坐标下土体增湿差异膨胀的参数表达

膨胀土是各种成因类型生成的裂隙介质体，有的颗粒平行定向排列，有的随机排列定向度差，水沿平行方向楔入，将使集聚体层产生扩展，垂直膨胀较大[12]，因此膨胀土普遍呈现出水平和竖向膨胀量不同的差异膨胀性特点。通过无荷膨胀率试验数据，考虑室内土工试样的几何形状和边界条件特点，建立柱坐标下土体的增湿差异膨胀模型，并反算得到水平和竖向的湿度线膨胀系数。

无荷膨胀率试验采用高20 mm、内径61.8 mm的环刀，切取击实土样，测量浸水后的无荷膨胀率。因此，土体试样几何形状为圆柱体，顶部无约束，底部提供竖向支承，侧面受到环刀壁的径向位移约束，为此建立柱坐标系下的各向异性增湿膨胀本构模型。

边坡稳定性分析一般采用平面应变模型，其水平和竖向的湿度线膨胀系数应不同，因此，可用柱坐标系下得到的径向、竖向线膨胀系数β1、β2代替平面应变问题中的水平、竖向膨胀系数。当土体为各向同性时，吸湿膨胀为均匀膨胀[4-5]，本构方程为式(5)，即应变为应力产生的变形与膨胀变形之和，总变形各向差异由应力效应引起。

(5)

考虑吸湿的水平、竖向的差异膨胀时，总变形各向异性由应力效应和差异膨胀共同构成。对此，采用由应力产生的变形与差异膨胀变形之和的应变本构形式。柱坐标系下，由环向与径向膨胀系数取值相同，引入式(3)的增湿应变增量表达式，叠加了增湿膨胀作用的应变分量如式(6)所示。当土体受到约束作用时，荷载以及膨胀变形将分别引起土体中产生各向异性的附加应力。

(6)

式中，η=β1/β2，定义为差异膨胀系数；μ为泊松比。

根据无荷载膨胀率试验土样边界条件εθ=εr=0，σz=0，εz=δH，由式(6)得到β2的表达式

(7)

式中，δH为无荷膨胀率；Δw为无荷载膨胀率试验始末的含水率差值，%。

1.3 土体差异膨胀模型的有限元验证

利用无荷膨胀率试验对应建立ABAQUS模型，对热膨胀比拟增湿差异膨胀进行验证。根据环刀内部土样尺寸建立计算模型(图1)，采用八节点三维实体单元(C3D8)进行网格划分，底面施加z方向位移约束，侧壁施加径向位移约束，取弹性模量30 MPa，泊松比0.3。程序中设置材料为膨胀属性，在预定场中设置初始温度和升高后温度，以模拟增湿膨胀。根据文献[6]中3种膨胀土样的无荷膨胀率试验数据进行有限元计算，结果与实测数据列于表1。

图1 模型网格

无荷膨胀率数值计算结果与文献[6]试验数据非常接近，相对误差为0.02%～0.08%，因此可用增湿膨胀的热膨胀等效模拟方法，进行膨胀土吸湿后各向异性膨胀的分析。

表1 试验与数值计算结果对比

注：w0为试验前含水量，wt为试验后含水量，VH为无荷膨胀率，ΔHs为无荷膨胀量，T0为初始温度，Tt为升高后的温度，α1为水平温度线膨胀系数，α2为竖向温度线膨胀系数，ΔHm为数值模拟的膨胀量。

2 膨胀土边坡有限元强度折减模型

2.1 算例边坡与膨胀土物理力学指标

以吉林省某新建客运专线膨胀土边坡工程为背景，进行考虑差异膨胀作用的有限元稳定性分析。边坡剖面如图2所示，上覆土层为残坡积红褐色黏性土，表面存在裂隙，土质较软，往深部裂隙逐渐减少；下伏基岩为泥质层状白垩系泥岩、砂岩。

按照《铁路工程土工试验规程》(TB10102—2010)[12]，通过现场取样进行室内试验，确定基本物性指标见表2。

表2 土样物性参数

注：w1为天然含水量，ρ0为天然密度，wp为塑限，Ip为塑性指数，gs为土粒比重，Fw为自由膨胀率。

图2 边坡剖面

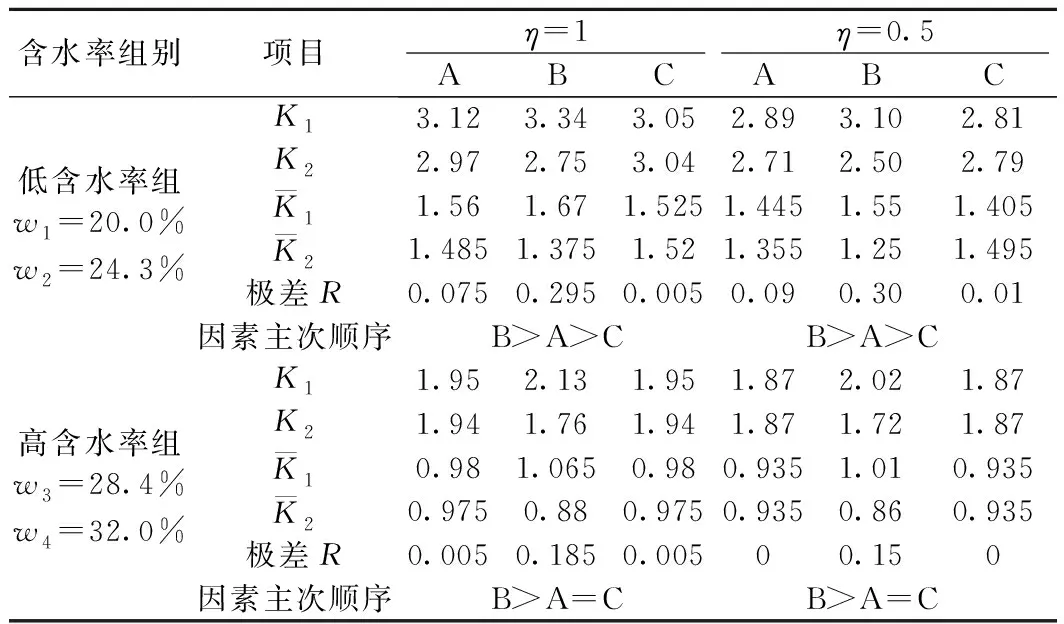
根据膨胀土的五指标(塑限、塑性指数、<5 μm颗粒、自由膨胀率及胀缩总率)分类判别法[13]，40%

分别配制含水率w为15.0%、20.0%、24.3%、28.4%和32.0%的土样进行无荷膨胀率试验，结果列于表3。可见，随初始含水率增加，土体的无荷膨胀率降低。当初始含水率较低时，土体有很大的膨胀势，遇水产生较大膨胀变形，而随土体含水率继续升高，由于前期膨胀势已部分释放，膨胀变形增量将减小。

表3 无荷膨胀率试验结果

控制压实度85%进行击实法制样，测定土样在各含水率下的重度和反复剪切强度参数，如表4所列。

表4 边坡土体力学参数

土体重度、强度参数分别与含水率呈正、负相关关系，原因是亲水性黏土矿物吸附一定量水，形成黏滞水膜，使土体重度增加，同时降低黏聚力和颗粒间的接触摩擦作用。

2.2 考虑差异膨胀作用的边坡有限元建模

首先，采用式(5)、(6)的热胀等效弹性本构方程建立边坡土体和基岩的平面热应力有限元计算模型，得到与湿度膨胀分量对应的应力场和变形场；然后，建立以基岩为弹性体，滑体为采用Mohr-Coulomb屈服准则的理想弹塑性模型(c、φ取值见表4)，其他参数、边界条件与热应力模型一致；最后，以热应力模型计算的膨胀变形和重力引起的地应力作为初始条件，导入第二步弹塑性体模型，得到考虑膨胀和重力共同作用下应力场和变形场。

根据边坡剖面特征，建立膨胀土边坡ABAQUS平面应变模型，坡高21.8 m，坡率1∶2.75。土体和基岩采用线弹性体模型，土体弹性模量取30 MPa，泊松比为0.3，重度见表4。基岩重度24 kN/m3，弹性模量3×104MPa，泊松比0.25。均采用四节点平面应变单元(CPE4)进行网格划分，模型底部约束x和y方向的位移，左右两侧约束x方向位移，如图3所示。

图3 有限元单元网格划分(单位：m)

利用无荷膨胀率试验结果(表3)，根据式(7)计算各向同性膨胀(η=1)与差异性膨胀(η=0.5)条件下由含水率w0=15%分别变化到wt=20.0%、24.3%、28.4%及32.0%的湿度线膨胀系数，进行ABAQUS的膨胀材料特性赋值，计算4种含水率条件下边坡模型的膨胀变形δ(表5)。

表5 膨胀参数和变形

2.3 边坡稳定性强度折减法分析

有限元强度折减法的基本原理[14]是将土体强度参数c、tanφ值同时除以折减系数Fr，得到如式(8)、式(9)的折减强度参数cm、tanφm，通过不断增加折减系数Fr，直至达到边坡稳定临界状态，此时折减系数Fr即为稳定安全系数Fs。有限元强度折减法能自动得到边坡滑动面的几何特征和稳定性系数，不再需要条分法的滑面形状、位置和条间力假设。

cm=c/Fr

(8)

tanφm=tanφ/Fr

(9)

式中，c和φ为土体抗剪强度参数；cm和φm为维持平衡所需要的或土体实际发挥的抗剪强度参数；Fr为折减安全系数。

有限元强度折减法中边坡失稳临界状态的判断依据有3类：①塑性区贯通；②滑面处节点位移和塑性应变的突变；③静力平衡的有限元计算不收敛。理论上，边坡失稳原因在于塑性区由坡脚至坡顶贯通，产生塑性流动，位移因此无限增长，造成有限元计算无法迭代收敛。因此3类判断在理论上具有统一性和一致性[15]，计算中以塑性区贯通为边坡失稳的判断依据。

3 边坡稳定性影响因素正交设计

膨胀土边坡稳定性主要受土体增重、强度降低及膨胀作用三项因素影响，为确定各因素的主次关系，针对显著性因素采取相应措施，需要对影响因素进行作用效应和敏感性分析。正交试验分析采用规格化的“正交表”，从大量的影响试验结果的因素中选出若干个代表性较强的试验因素，通过综合比较试验结果，可得到各因素对试验结果影响的主次顺序[16]。正交试验的试验点具有“均匀分散，齐整可比”的特点[17]。正交试验分析包括两部分，即试验方案设计和结果分析。

首先，需确定试验结果的衡量指标；然后，选定试验因素并且确定各因素水平；最后，根据试验因素和试验水平选择正交表。文中采用膨胀土边坡安全系数Fs为控制指标，差异膨胀系数η、膨胀变形δ、土体的强度参数c、φ和重度γ为边坡稳定影响因素。其中，δ、c、φ和γ与含水量相关且为试验测得，η可人为假定并进行比较。因此，须对η进行单因素分析，对δ、c、φ和γ进行正交试验分析，暂不考虑影响因素之间的交互作用。

为研究不同含水率阶段各因素对边坡稳定性影响，分别在低初始含水率组w1=20.0%、w2=24.3%和高初始含水率组w3=28.4%、w4=32.0%条件下，取η=1和η=0.5进行正交试验方案设计。选择L4(23)正交表，表中元素取膨胀变形(δ)、土体强度(c、φ参数数据对)和土体重度三因素，各因素对应两个水平，如表6所示。

表6 试验因素和水平

4 影响因素作用效应与主次关系

4.1 强度折减安全系数的正交试验极差分析

基于有限元强度折减法，根据边坡失稳临界状态判据③，得到强度折减安全系数Fr。塑性变形(PEEQ)等值线如图4所示，塑性贯通区与实际滑动面基本相符。

图4 塑性变形等值云图

正交试验结果分析常用的两种方法是极差分析法和方差分析法。采用较为直观的极差分析法展开研究，其包含计算和判断两步，如图5所示。

图5 极差分析示意

(10)

Rj越大，表明该因素水平的波动对试验指标影响也越大。根据各因素Rj大小，可以判断试验因素对试验指标影响的主次顺序。因此，可以通过极差分析得到膨胀土边坡稳定性影响因素(土体增重、强度降低及膨胀作用)的主次关系。

表7列出低含水率组(w1=20.0%、w2=24.3%)和高含水率组(w3=28.4%、w4=32.0%)在差异膨胀系数分别为1和0.5试验方案和结果。对表7结果进行极差分析，如表8所示，其中A、B、C代表试验因素分别为膨胀变形、土体强度参数、土体重度，1、2代表因素的水平，表中每一行的因素水平组合即为一个试验方案。

4.2 影响因素作用效应的主次排序

从表8的因素主次顺序可看出，土体初始含水率较低时(w≤24.3%)，土体软化对膨胀土边坡安全系数影响最为显著，强度值由水平1变化到水平2，安全系数降低最为明显，土体强度成为控制因素。膨胀作用引起的安全系数降低次之，边坡安全系数受土体增重影响相对最小。随含水率的升高(w≥28.4%)，膨胀作用、土体增重对边坡稳定性影响进一步降低，而土体强度始终为控制因素。

表7 正交试验方案及结果

表8 极差分析

为分析差异膨胀性对边坡稳定性的影响，取表7中低含水率组和高含水率组中的边坡安全系数进行比对，汇于表9。

表9 不同含水率组别下的边坡安全系数

可以看出，差异膨胀性对边坡的稳定性有一定影响，土体初始含水率较低时，较之采用各向均匀膨胀，考虑差异膨胀计算得到的安全系数低0.11～0.13；随含水率的升高，差异膨胀系数η取1和0.5计算得到的边坡稳定安全系数相差不大，差异膨胀性的影响减小。

因为含水率在较低范围内变化时，土体的膨胀势大，各向异性膨胀变形对差异膨胀系数敏感；而含水率达到一定值后，膨胀土充分吸水软化，土体强度成为控制边坡稳定的主要因素，差异膨胀性对边坡稳定性计算结果影响变小。

5 结论

针对膨胀土边坡稳定性受土体增重、强度降低及膨胀作用的影响因素主次关系及敏感性问题，基于考虑水平、竖直差异膨胀的热胀比拟模型，采用有限元强度折减法结合正交试验，开展稳定性膨胀土边坡稳定性及影响因素作用效应分析，得出以下结论。

(1)基于热膨胀比拟增湿膨胀原理，推导了土体柱坐标下考虑水平、竖直差异膨胀条件的应力应变方程，提出了由简便的无荷膨胀率试验确定差异膨胀参数的公式，并通过对应的热膨胀有限元模型进行了验证，数值计算结果与试验结果非常接近，相对误差为0.02%～0.08%。

(2)算例分析表明，三项因素综合作用下，初始含水率较低时，强度降低是导致边坡失稳的主要因素，膨胀作用次之，土体增重则相对影响较小。随含水率升高，膨胀作用、土体增重影响减弱。

(3)土体各向异性膨胀对边坡稳定有不利影响。土体初始含水率较低时，考虑土体客观存在的水平、竖直差异膨胀性，计算得到的安全系数较各向均匀膨胀模型低0.11～0.13，随含水率的升高，差异膨胀性的影响减小。