《比的认识》教学案例
马旭光
【教学内容】
苏教版六年级上册第53~54页。
【教学过程】
一、创设情境,激发兴趣
(出示洗洁液的稀释瓶)
师:同学们见过这种瓶子吗?知道这种瓶子是做什么用的吗?(配制洗洁液的,可以根据需要将洗洁液原液进行稀释)
师:(指着屏幕)你知道在配制溶液时,瓶子下方白色部分装的是什么?(水)蓝色部分呢?(洗洁液)
师:以其中的一个刻度为例(出示),说说你能从中获得哪些信息?
(洗洁液看作1份,水是4份;水的体积比洗洁液多3份,洗洁液的体积比水少3份;水的体积是洗洁液的4倍,洗洁液的体积是水的)
师:两个数量相比较,既可以用减法比较两个数量之间相差多少,也可以用除法或分数来表示两者之间的倍数关系。其实,两个数量之间的关系还可以用一种新的表示方法,知道是什么吗?对,今天我们就一起来认识比。(板书课题)
【设计意图:把学生熟悉的安利塑料瓶作为课程资源,拉近了学习内容与现实生活之间的距离,让学生能够真实地感受到“比”这一知识的存在,体验到数学与生活的联系。同时引导用已学知识表示两个量之间的关系,为“比”也可以表示两个量之间的关系做了铺垫。】
二、自主探索,合作交流
1.教学比的各部分名称。
师:看到这个课题,你想学到哪些知识?
(出示:水与洗洁液体积比是4比1)
师:比的读法、写法、各部分名称是什么呢?请同学们翻开教材第68页,自学例1。(学生自学)
师:1比4可以怎么写?你还学到了什么?
师:那水与洗洁液的比4比1可以怎么写呢?哪位同学愿意到黑板上来写?
(学生板演,其余学生在本上写)
师:这个比读作?比的前项是几?后项是几?
师:同学们看黑板上的两个比,你有什么发现?在小组内说一说。(学生交流后汇报)
小结:调换比的前后项位置,就会得到一个新的比,它的意义也就不同。因此说比时,一定要说清楚是哪个数量与哪个数量在比,不可颠倒顺序。
【设计意图:在学生已有知识的基础上,引出比,认识比,使学生体会到同类量可以用比来表示,比是对两个数量进行比较的又一种数学方法。】
2.教学比的意义和比值。
(1)认识不同数量之间的比。
出示:走一段900米长的山路,小军用了15分,小伟用了20分。
师:看到这些条件,你能求什么?(根据学生的回答,板书:900÷15=60 900÷20=45)
师:你是怎么求出速度的?(速度=路程÷时间)
师:其实我们也可以用比来表示路程和时间的关系。你们会吗?
(出示:小军走的路程与时间的比是900∶15)
师:谁能说说小伟走的路程和时间的比呢?
(出示:小伟走的路程和时间的比是900∶20)
(2)认识比的意义及比值。
师:通过刚才的学习,你认为比与什么有关?
(小组讨论)
师:两个数的比就表示两个数相除,那么用比的前项除以后项所得的商叫做比值。
师:算算900∶15这个比的比值是几?想一想,900∶20 这个比的比值是多少?那 1∶4 和 4∶1 这两个比呢?这两个比值60、45也就表示什么?这几个数就分别表示这几个比的比值。
出示:求下列比的比值。(学生口答)
9∶3 = 2.4∶2= 2∶5=
(3)小组讨论:比与比值有什么区别?
小结:比表示两个数相除的一种关系,由前项、比号、后项组成。比值表示比的前项除以后项所得的商,是一个数,可以是分数、小数或整数。
(4)教学比的分数形式以及比与分数、除法之间的关系:出示第69页的“试一试”。
师:你认为比与什么有联系?(口答)
师:它们之间又有怎样的联系?通过讨论完成下表:
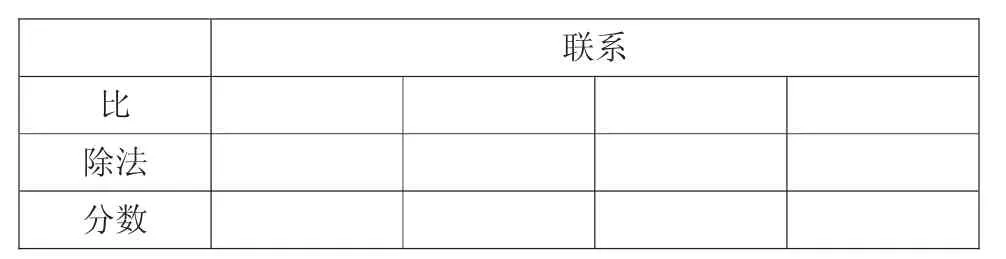
联系比除法分数
师:比与除法和分数之间有着密切的联系,因此两个数的比也可以写成分数形式。如,2∶3也可以写成,在表示比时仍读作2比3。
师:如果用字母a表示比的前项,字母b表示比的后项,你能用字母表示出三者之间的关系吗?
小结:比的后项,除法的除数,分数的分母都不能为0。
师:在学习的过程中,你还有哪些疑问?
【设计意图:通过教学,使学生进一步完善对比的认识。在概括比的意义时,重点强调了比与除法、分数的关系,使学生对比的意义的本质有所理解。“你还有哪些疑问?”培养了学生的质疑意识。】
三、巩固练习
1.

涂色部分与空白部分的比是( ),比值是( )。
空白部分与涂色部分的比是( ),比值是( )。
2.下面是妈妈购买几种水果的总价和数量的记录。

品种 总价/元 数量/千克 单价/元苹果 15 3橘子 8 4香蕉 4.8 2
苹果总价与数量的比是( ),比值是( );
橘子总价与数量的比是( ),比值是( );
香蕉总价与数量的比是( ),比值是( )。
强调:这里总价和数量的比的比值实际就是它们的单价。
四、拓展提高
师:在平面图形当中会有怎样的比呢?
(介绍三角尺)
师:对边和斜边的长度会有怎样的关系呢?拿出作业纸,请同桌选择不同的三角形测量并填表。
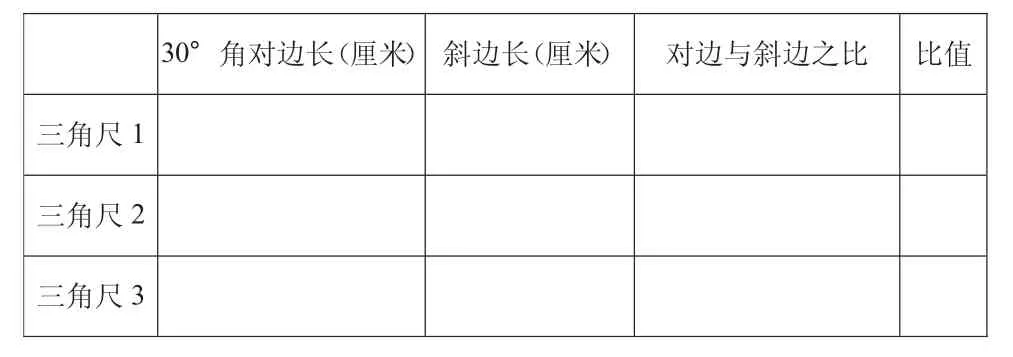
30°角对边长(厘米) 斜边长(厘米) 对边与斜边之比 比值三角尺1三角尺2三角尺3
(学生汇报,完成表格)
师:观察表格,你有什么发现?
生:直角三角形中,30°角所对的边长是斜边的一半。
五、总结延伸
师:通过这节课的学习,你有哪些收获呢?你认为自己表现得怎样?
【设计意图:由学生畅谈体会,有助于回顾本节课的知识,并且通过反思,加深对知识的理解。】
1.出示:你知道吗?名片、信用卡等宽与长的比都是10∶16,你知道为什么设计师都选择10∶16作为它们宽与长的比吗?这是因为这个比是一个黄金比,你听说过黄金比吗?
2.介绍黄金比。
公元前5世纪,古希腊哲学家、数学家毕达哥拉斯,通过长时间研究铁锤和铁砧的尺寸发现它们之间存在着和谐的比例关系,即比值约等于0.618时最为优美。黄金比在日常生活中有着广泛的应用。
3.出示名片,现在你能给老师的这个名片提点建议吗?
4.从这张名片上你知道老师有什么爱好吗?
(看足球比赛)
师:前不久“东亚四强赛上中国队以3∶0的比分完胜韩国队。”在这里的3∶0是一个比吗?你是怎么认为的呢?
【设计意图:这个过程既帮助学生加深了对比的意义的理解,又大大拓展了学生的知识面,进一步明白数学源于生活,用于生活。】

