《分数的再认识（一）》教学实录（一）

李 丽

【教学内容】

北师大版五年级上册第63、64页。

【教学过程】

一、唤醒旧知，揭示课题

师：同学们，我们在三年级时已经对分数有了初步的认识，现在老师要考考你们。（出示一张圆形纸片）谁能找到这张纸的？

（学生回答，教师配合演示，强调语言的规范性：把圆形纸片平均分成4份，其中的1份就是这张圆形纸片的）

师：今天我们继续学习有关分数的知识。［板书课题：分数的再认识（一）］

二、实际操作，探究新知

1.在整体中表示部分，再次认识分数。

（1）实际操作。

（学生操作，教师巡视指导）

（2）展示过程。

生：我把这个正方形平均分成4份（4个小正方形），将其中的3份涂上颜色，涂色部分就是这个正方形的（如下左图）

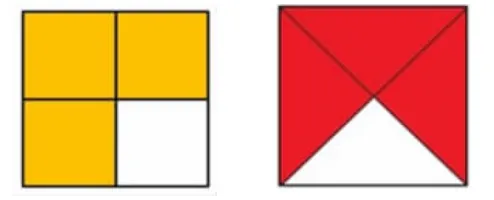
师：还有其他分法吗？

生：我是在正方形内画了两条对角线，也是把它平均分成了4份（4个小三角形），涂了3份。（如上右图）

师：他们分的方式不同，但什么是相同的？

生：都是把这个正方形平均分成4份，涂色部分表示这样的3份，也就是这个正方形的

生：我把这4个三角形先平均分成4份，每份是1个三角形，把3个三角形涂上颜色，涂色部分就是。（如下图）

师：这个整体是什么？

生：这个整体是4个三角形。

师：对。这4个三角形我们可以看作一组图形。

生：我先把这些骨头看成一个整体，再把它平均分成4份，每份是3根，把这样的3份也就是9根圈起来，圈起来的部分就是这个整体的（如下图）

师：你是把这个整体竖着分的，为什么不横着分？

生：横着一行一行地看是3份，竖着一列一列地看正好是4份。

师：这4份也可以说成4组，就是每3块骨头为一份，4份就是4组。

师：刚才我们是将一组图形看成一个整体，现在看来，四组物体也可以看成一个整体。

（3）揭示整体。

生：我们先后把一个图形、一组图形、四组图形平均分，这些都可以看成是一个整体。

（4）小结意义。

师：同桌说说什么是分数？

生：把一个整体平均分成n份，其中的几份，可以用分数表示。（引导学生在充分交流的基础上概括分数的意义）

师：真棒！把一个整体平均分成若干份，其中的一份或几份，可以用分数表示。（板书）

师：看来分数就是表示什么与什么之间的关系？

生：整体和部分之间的关系。

2.由部分还原整体，深化理解分数。

（1）实际操作。

（引导学生认真读题，找关键字，强调“一个图形”）

师：先请同学们静静地想，想好了再画图。

（学生操作，教师巡视指导）

师：很多同学设计的是规则图形，可以不是规则图形吗？

（2）展示过程。

（3）比较异同。

师：观察这些图形，你有什么发现？

生：总数都是8个。

生：总数虽然相等，但整体的形状不同。

师：同学们很会观察，会从部分倒推回整体，而且不会被表面现象迷惑，看问题能抓住关键，抓住分数的本质——部分和整体数量上的关系。真了不起！

3.体验整体量与部分量的相对关系。

（1）操作展示。

师：（出示三盒铅笔）每盒铅笔支数未知，你能拿出每盒铅笔的吗？请你只向全班出示拿的结果，不说出盒内的总支数，并力争用比较准确的数学语言表达拿的过程。

生：我把盒内的铅笔平均分成2份，拿出其中的1份，是1支。

师：这1支就是盒内铅笔总支数的多少？

生：我把盒内的铅笔平均分成2份，拿出了其中的1份，是2支，这2支铅笔是这个整体的

（2）质疑反思。

师：面对这样的结果，大家有什么发现？可以提出怎样的问题？

师：是呀，这是怎么回事呢？先独立思考，然后互相探讨。

生：因为总支数不同！

师：我们来推理一下，原来每盒内到底有多少支呢？

生：分别是2支、4支和8支。

（请刚才的三位学生开盒验证，结果正确）

师：通过刚才的游戏，你有什么发现？

生：有时候尽管是同一个分数，但是它们的整体不一样，拿取出来的部分数量也不一样。

（3）强化感悟。

师：同学们能不能举个生活中的例子说一说？

师：同学们说的都很好！同一个分数，整体不一样，部分数量也不一样；部分量多，说明整体就多，部分量少，整体就少。大家又发现了分数一个神奇的地方，为自己鼓鼓掌吧！

三、分层练习，巩固新知

1．基本练习。完成教材第64页“练一练”第2题。（学生先独立完成，再全班交流）

2.变式练习。

生：第一盒苹果有8个，第二盒有10个，第三盒有12个。

师：你怎么这么快就知道了？有什么好方法吗？