纵向读透教材让目标更理性
———《轴对称图形》教学设计与说明
强振宇 强震球(特级教师)
【教学内容】
苏教版三年级上册第83~85页。
【教材简析】
苏教版数学教材的“图形与几何”内容,在两个学段各安排了一个单元“轴对称图形”,这节课属第一学段教学内容——初步认识轴对称图形。教材安排了两个例题,例1通过蝴蝶标本、天坛祈年殿、飞机模型三个实物的图片,以及相关的举例初步认识“物体的对称”;接着把上述物体进一步抽象为平面图形得到“对称图形”;再通过“对折”等活动初步认识轴对称图形及其基本特征。例2通过剪松树图形以及用折、画、剪等方法“做”出不同的轴对称图形,让学生进一步积累感性认识,丰富对轴对称图形的体验,锻炼动手实践能力,培养一定的空间观念。教材这样的编排,立足学生第一次认识“轴对称图形”,既没有认识对称轴(在第二学段),也没有要求对常见平面图形“是否是轴对称图形”的判断。
有教师认为这部分内容简单,教学时只要按例题组织活动就行。实际上恰恰由于简单,学生不能把握“轴对称图形”的基本特征——完全重合;由于没有教学对称轴,判断是否是轴对称图形,要依赖动作思维,脑子里先进行对折,再通过空间想象才能判断,学生的直观思考能力没有得到强化。因此,教学时要抓住“完全重合”、直观“对折”展开,让学生感知数学的对称美。本课精心设计练习,挖掘智力价值,达成学段教学目标。
【教学准备】
课件、学生剪下的课文第107、109页的图形、一张长方形(正方形)彩纸、1把剪刀等。
【教学过程】
一、实物导入,明确方向
师:老师给大家带来了一个蝴蝶标本,从运动方式看,蝴蝶翅膀是什么运动?(旋转)这是一个飞机模型,飞机机身是什么运动?(平移)
师:今天,我们换个数学角度研究这些物体,可以研究这些物体的什么?(板书:形状)
【设计说明:本学期对物体的研究,一个是质量,一个是运动现象。前面学生刚刚学习了物体平移和旋转,课始直接呈现比较熟悉的两个实物,唤醒学生对实物以前的数学理解,然后以问题为引领,切入需要关注研究的主题,激发学生对新知学习的原动力。】
二、观察比较,认识对称
1.感受对称。
师:这是一幅北京天坛祈年殿的图片。请大家仔细观察蝴蝶标本、飞机模型、天坛祈年殿这三张图片,它们的颜色、用的材料都不一样,形状有什么共同的特征?(板书:对称)
师:谁能具体解释一下“对称”的意思?(板书:左右、上下;两边形状一样、大小一样)
小结:像这样左右或上下两边形状、大小都一样,两边完全相同的物体就是对称的。
2.举例对称。
师:生活中还有哪些物体也具有这样对称的特征?老师也给大家找到一些对称的例子。

3.对称图形。
师:现在把对称的蝴蝶标本、天坛祈年殿和飞机模型都画下来,就可以得到三个平面图形(如下图)。这些图形还是对称的吗?
(板书:图形)

师:可不要太相信自己的眼睛哦!有办法用事实说话吗?(板书:对折)
生:将飞机的平面图形上下对折,发现上下两面是完全一样的,也就是上下对称,所以是对称图形。
(学生动手操作其余两个图形的对折:左右对折)
【设计说明:第一学段教学轴对称图形是引导学生通过认识对称物体来认识轴对称图形的,而掌握轴对称图形基本特征的前提是感知理解“对称”。对第一次接触“对称”的学生来说,虽然对称现象在生活中很常见,对它有意识的关注程度却不是很高,因此,教学时在重要属性——对称上下足功夫,将观察法与实际操作“对折”有机结合,加深学生对“对称”意义的理解。】
三、操作感悟,自主建构轴对称图形
师:继续,比一比、看一看对折后的图形,你发现了什么?(只看到原来图形的一半了,这是什么原因?这是以什么为界线的?也就是说明两边图形怎么样?——揭示:两边图形完全重合是轴对称图形)
(板书:完全重合 轴)
师:蝴蝶、祈年殿、飞机三个平面图形为什么是轴对称图形?
折痕处画上一条点划线(课件上画出:—·—·—·—) 表示“轴”,特征就更明显。
师:老师这儿还有两个图形(如下图),它们是轴对称图形吗?为什么?

图1 图2
讨论图1:折一折——两边图形完全相同,对折后发现不能重合(部分重合)。
讨论图2:折一折——两边图形不同,对折后只是部分重合。
强调小结,轴对称图形的关键词:对折、完全重合。
【设计说明:“对折”“完全重合”是判断轴对称图形的重要属性。教学中先提供足够的正例,再借助对反例的辨析,扫清对“完全重合”的理解障碍,学生在动手对折、动眼观察、动脑比较、动口表述中很好地形成“轴对称图形”的直观理解,为后续判断轴对称图形储备经验。】
四、动手操作,深化认识轴对称图形
1.观察判断,内化认识。
(1)下面的图案,哪些是轴对称图形?(说理由)

(2)下面的英文字母,哪些可以看作轴对称图形?为什么?

(3)这些平面图形,哪些是轴对称图形?(教材109页)
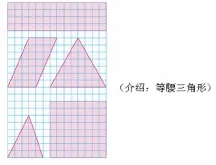
讨论:平行四边形为什么不是轴对称图形?
2.“做”轴对称图形,深化认识。
(1)剪松树图形。
师:(出示松树图形)用一张正方形的纸怎样可以剪出这个松树图形?
小结方法:对折——画一半松树图形——沿线剪——展开。
(学生动手画、剪)
师:剪出的是轴对称图形吗?为什么?
(2)各自剪一个轴对称图形:先想好准备剪什么,再剪一剪。
(3)下面的图案是从纸上剪下来的,是哪一张?连一连。

【设计说明:在学生刚刚掌握轴对称图形的特征时提供一组图案、一组英文字母、几个常见平面图形的判断,既是为了强化学生对特征的理解,更是培养学生对轴对称图形的直觉思考能力,同时也为动手“做”轴对称图形提供经验,丰富学生对轴对称图形的体验,进一步积累感性认识。】
五、分层练习,逐步提升,发展思维
1.下面的交通标识,哪些可以看作轴对称图形?

2.选一选:一张圆形纸,先左右对折一次,再上下对折一次,然后用剪刀剪去一个角,中间剪去一个小三角形。打开后,是哪个图形?能用今天的知识解释一下吗?

六、总结强化,拓展延伸
1.今天有哪些收获?有什么感受?
2.课后思考:四个相同的小正方形拼成一个图形(如下图),添上一个同样的小正方形,使图形成为一个轴对称图形,这个正方形该怎么放?


