条子图之含“双比”的应用题
刘善娜
【教学时机】
人教版六年级上册分数除法单元学习后。“双比”应用题,是指问题中含有两个“比”的应用问题。
【教学目标】
1.通过画包含两个相关比的应用问题的直条图,从“份数”视角进一步理解“比”。比与分数可以转化,深度理解比,也有利于形成更简捷合理的分数问题解题策略。
2.掌握较为直观的直条图的基本画图技巧,为后续分析理解较难的应用问题打下基础。
【教学过程】
一、理解“比的转化”
出示题目:甲∶乙=5∶3 ,乙∶丙=4∶3。甲∶乙∶丙=?
师:这两个比中的谁是不变的?如何统一、转化?
小结:为了清楚哪个份数不变,需要统一成一样的份数,我们可以把它圈一下。板书:

【设计意图:两个相关的比的转化,是画比问题的相关条子图的重要知识基础。如果学生基础不扎实,可以多练几题。】
二、典型问题形成技能:其中一个量不变
2.师生交流,示范作图。
师:这道题的正确率有些低。如果想掌握更简单的方法来攻破这类题,就请同学们跟着老师一步一步地画图。
【设计意图:这类单位“1”变化的分数问题,学生会感到有一定的难度,正确率很低。即便通过分数问题的方法去找“量率对应”来解决这类问题,学生也觉得非常抽象,不容易理解。因此在学生解答后,教师快速核对答案、统计正确率,激发学生寻求比“量率对应”更简单的解题方法的需要。】
问1:画图时要先把已知的信息画出来,这个问题中你能看到两个比吗?先画7∶5,男生∶女生。再画第二个比,也是男生∶女生,是9∶7。两个比中,有人数相同的或者说没有发生变化的份数吗?
小结:男生人数没有变化,所以“9”和第一个比中的“7”一样长,代表的是一样多的男生人数。女生人数要比原来的长一些,因为多了“12人”。

问2:两个比中有相同的量,能否把相同的量转化成相同的份数?
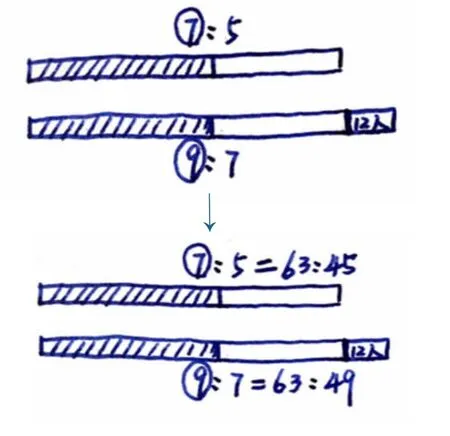
问3:现在,你可以从图上看到女生“份数”的变化吗?
生:女生人数从45份变成49份,多了4份,多了12人,1份就是3人。男生有这样的63份,就是63×3=189(人)。
问4:在两个比的应用题中,画条子草图的关键是什么?
小结:找到两个比中相等的或者不变的量,转化成一样的份数,就能从图中算出1份是多少。
【设计意图:这类含两个比的应用问题,属于比中的其中一个量发生了变化,总量也发生了变化,要利用不变的量转化两个比,学生就能在条子图上清楚地看到“份”的变化,从而求出“1份”的量。从直观出发,强调“不变的量”。】
3.尝试,训练。
(1)某班女生人数与男生人数的比是4∶5,最近又转来一名女生,结果女生人数是男生人数的现在全班有学生多少人?
4.方法小结。
在两个比的应用问题中,画条子图的步骤为:找到不变的量,长度对齐→转化比,使不变量的份数相同→观察变化的份数。
【设计意图:第(1)小题完全是模仿性训练,在交流反馈后进一步归纳作图方法,强调画出“不变的量”;第(2)小题需要转化一步,通过找出“不变的量”是女生人数进一步感受找“不变的量”来作图的基本策略。】
三、典型问题形成技能:两个量的总量不变
1.呈现问题:修一条公路,已修的与剩下的比是1∶3,再修 30 千米,已修的与剩下的比是 2∶3,这条公路长多少千米?
师:两个比中,什么量不变?
小结:已修的和剩下的都在变,总数“一条公路的总长”才是不变的。两个比的变化问题,可能是其中一个量不变,也可能是总量不变。
【设计意图:六年级学生要学会分析问题的特征,分析相关问题的异同。因此,呈现略有变化的题型时,要多让学生说说有什么变化,了解一类问题的类型有哪些,做到心有问题的“全局结构”。】
2.师生交流,逐步成图。

核心问题:什么量不变?(把不变的圈起来)怎么转化?
3.模仿跟进。
(2)两块一样重的铜锌合金,第一块铜与锌的比是1∶4,第二块铜与锌的比是3∶4,把它们合成一块,铜与锌的比是多少?
【设计意图:第(1)小题是模仿性训练,与例题一致,仍然强调画出“不变的量”,再转化;第(2)小题不变的总量以“相等”的形式出现,略有变式。画图策略上没有变化,继续训练技能。】
4.再次回顾方法。
四、全课总结
师:关于画这类条子图,你有什么收获?
【教学建议】
两个比的应用问题,是分数应用题的一种。教师可以从“份数”的角度切入,利用画条形图所必须思考的“谁与谁对齐,一样长”的问题,将核心问题从隐性切换到显性,从“量率对应”的抽象走向“几份变成几份”的直观。在实际教学中,有两点建议:
一、教学“比”的概念时,强调“份数”意义
认识“比”的时候,要让学生更多地认识其“份数”的意义。在学生掌握比的概念后,可以将原来较为简单的分数问题转化成比的应用问题,不要将比的应用局限在“按比例分配”问题。
二、后续再加一个课时,对比沟通“分数问题”与“比的问题”的画法、解法
画数学课程中有“画线段图解决较复杂的分数问题”一课。当学生学完含两个比的应用问题后,后续需要再跟进一课时,关注分数典型问题和比的应用问题的沟通,对比线段图和条子图,发现其中的联系和差异,有助于学生掌握灵动的、联通的解题策略,而不是就题论题,就类型画图。

