几种统计软件建立ARIMA模型的应用比较

钱 俊，王永波

（南方医科大学 生物医学工程学院，广州 510515）

0 引言

20世纪70年代，Box和Jenkins提出了自回归移动平均模型，即ARIMA模型，也称Box-Jenkins模型。ARIMA模型被广泛应用于时间序列资料的分析，成为经典的时间序列分析和预测方法，现在一般提的时间序列模型，指的是该模型或其某种表述形式[1]。ARIMA模型精确度较高但计算复杂，一般需借助软件实现。目前，常用统计软件如SAS、SPSS、R和EVIEWS都有ARIMA建模模块，这给模型的推广应用提供了强有力的技术支持[1-4]。

在经典的ARIMA模型中，如果时间序列存在趋势且经过d阶逐期差分可以平稳，则可以建立ARIMA(p,d,q)模型[3]。设{Xt}为非平稳序列，d阶差分后的平稳序列为{Zt}，即有 Zt=▽dXt(t＞d)，若{Zt}是 ARMA(p,q)序列，则{Xt}称ARIMA的d阶求和序列，并用ARIMA(p,d,q)表示。模型的一般形式：

式（1）中，p、q为自回归和移动平均阶数，d为平稳化过程中差分的阶数；ϕ(B)和θ(B)分别为自回归算子和移动平均算子。若时间序列存在季节性周期波动，则需要加入季节性算子。对于包含有季节和趋势的非平稳序列，如果可以通过逐期差分和季节差分使序列平稳化，就可运用ARIMA(p，d，q)(P，D，Q)S模型，一般形式：

式（2）中，P、Q为季节性的自回归和移动平均阶数，D为季节差分的阶数，s为季节周期。ΦP(Bs)为季节性P阶自回归算子；ΘQ(Bs)为季节性Q阶移动回归算子。式（2）称为SARIMA模型或乘积季节ARIMA模型，是随机季节模型与ARIMA模型的结合，用来描述由于季节性变化（包括季度、月度、周度等变化）或其他一些因素引起的周期性变化的序列[3]。SARIMA模型属于ARIMA建模中较复杂的情形，本文以此情形为例阐述其建模过程。

1 数据来源和建模步骤

本文利用广东省2009年1月至2015年12月痢疾的月发病例数进行时间序列分析[5]。通过对发病例数的观察，该数据呈明显的非平稳性和季节性，并伴随一定的周期性波动，根据原始数据序列图以及疾病的发病特点，拟建立SARIMA模型。

将该段观察时间序列分为2009年1月至2015年6月和2015年7月至12月两段，前者用于模型的建立，后者用于评价模型预测效能。虽然ARIMA建模的操作并不复杂，但要建立一个好的或较优的模型却并非易事[6,7]。数学理论已证明，ARIMA模型的形式并不唯一。尽管不少软件中有自动建模的程序，如SPSS中的专家建模器以及R软件的auto.arima()命令，但这些都有局限性。任何软件都不可能编得很复杂，不可能对所有参数和模型形式都做详尽的测试，因此自动建模得到的结果并不一定是“最优”，理想的模型仍需研究者自行比较和判断[1,7]。一般ARIMA建模包含3个步骤：模型识别、参数估计、模型检验（诊断），通过对这3个步骤的反复进行，筛选出“最优”模型并进行预测[6]。在模型识别阶段，根据ACF和PACF的图形特征，判断ARIMA模型的阶数，这是一种直观方法。另一种方法就是尝试阶数p和q不同的取值，利用AIC、BIC等准则，选择“最优”模型[7]。最后得到的模型应具备两个要素：模型的残差序列需通过白噪声检验；在模型参数的简约性和拟合优度指标的优良性方面取得平衡[1]。

2 软件建模应用及结果分析

下面分别运用SAS 9.2、SPSS 20、EVIEWS 6.0、R3.3.2这4种软件建立SARIMA模型，并对建模的步骤和计算结果进行分析。

2.1 SAS建模

在SAS/ETS软件中，ARIMA建模可以通过编程实现，也可以运用菜单过程步。一般而言，SAS编程建模更为灵活实用，也更符合使用习惯，本文在编程环境下说明建模的过程：（1）创建数据集

导入2009年1月至2015年6月广东省痢疾的月发病例数，通过intnx()函数创建时间，然后输入发病例数。

input x@@;/*定义月发病例数变量*/

t=intnx('month','01jan2009'd,_n_-1);/*创建时间集*/format t monyy.;cards;353,411…;/*定义时间格式，导入数据*/

（2）模型识别

调用程序PROC GPLOT，绘制序列图{Xt}，观察数据的平稳性（图1）。经观察发现序列呈现一个略降的长期趋势和一个周期长度为一年的稳定的季节变动。因此首先消除季节影响，对该序列做12步差分，然后为了消除长期趋势的影响，运用dif()函数对原始序列进行差分，发现一次差分后序列{∇∇12Xt}基本平稳，则d=1和D=1，s=12。

图1 广东省痢疾的月发病病例数时序（SAS）

在SAS中PROC ARIMA程序功能强大，其含有IDENTIFY（模型识别），ESTIMATE（参数估计），FORECAST（短期预测）这三条命令。为了进一步判断其平稳性，调用PROC ARIMA程序中IDENTIFY命令对序列进行识别，考察差分后序列{∇∇12Xt}的ACF和PACF图，初步判断模型中阶数p=1,q=1。但为了避免主观判断偏差，再运行IDENTIFY命令中自动识阶选项MINIC()，计算指定范围内“最优”模型的阶数。运行得最小BIC(0，1)=7.7388，判断可能最优模型的阶数p=0,q=1。再根据图中ACF和PACF图形在k=12处显著，k=24处不显著，初步判断季节效应的阶数P=1，Q=1。

proc arima; /*建立ARIMA模型*/

identify var=x(1,12)nlag=24 minic p=(0:5)q=(0:5);/*判断最优模型的阶数*/

（3）参数估计

调用PROC ARIMA程序中ESTIMATE命令，对可能的最优模型SARIMA(0,1,1)(1,1,1)12进行参数估计；结果显示常数项以及参数P=0和Q=0的原假设检验P值大于0.05（表1），结果不显著。说明此模型并非最优模型。

proc arima;estimate p=(12)q=(1)(12);/*拟合带常数项的SARIMA模型*/

表1 备选模型的参数估计及检验（SAS）

（4）模型检验

在延迟6阶，12阶和18阶的Ljung-Box统计量(LB统计量)检验的P值全部显著大于0.05，此模型的残差属于白噪声序列（表2）。但由于参数估计得到的系数并不符合“显著性”要求，需对模型的阶数进行调整。在自动识阶的过程，根据BIC准则，BIC(0，1)=7.7388最小，BIC(1，0)=7.7498次之，BIC(1，1)=7.7985较小；而季节模型的阶数P和Q的取值一般不超过2，对上述参数组合的取值进行试验，重复步骤（3）和步骤（4）进行比较。根据模型参数估计，拟合效果以及残差白噪声检验的结果进行综合判断筛选最优模型，则SARIMA(1,1,0)(0,1,1)12为最优模型。该模型所有参数都通过了显著性检验（表1）；残差通过白噪声检验（表2）；拟合优度检验的统计量中，除指标BIC略高，其余各项指标值AIC、SBC等均最小（表2），此时得到“最优”模型的数学表达式：

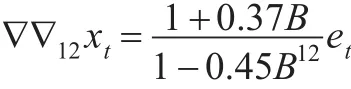
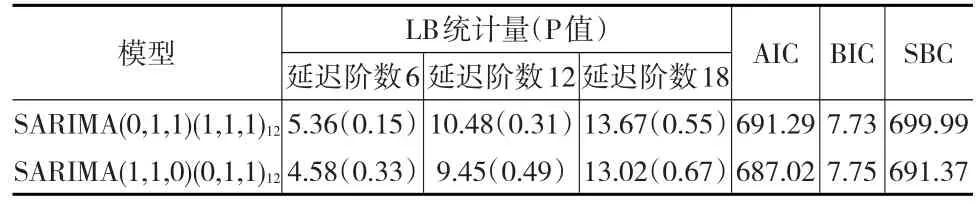
表2 备选模型的残差白噪声检验和拟合优度检验（SAS）

（5）预测

运用SARIMA(1,1,0)(0,1,1)12模型对2015年7月至12月痢疾的发病数进行预测，可以得到具体预测值以及区间估计值（图2）。将实际值和预测值进行比较，结果显示，各月实测值都落入了预测值的置信区间内，拟合平均相对误差MAPE=10.63%，预测平均相对误差10.33%，该模型具有较好的预测效能（见下页表3）。

proc arima;estimate p=1 q=(12)noconstant；/*拟合不带常数项的模型*/

forecast lead=6 id=t out=out;/*预测后6个月的数据*/

图2 SARIMA(1,1,0)(0,1,1)12模型的预测值和置信度为95%置信区间（SAS）

表3 SAS、SPSS、EVIEWS、R软件操作ARIMA模型的比较

SAS编程建模的过程中，每个步骤都能得到比较详尽的结果，建模方法灵活，功能强大。比如，模型识别时，可以自动识阶；参数估计时可以选择条件最小二乘法、无约束最小二乘法和最大似然法，nonconstant选项则模型不带常数项[8,9]。

2.2 SPSS建模

SPSS中的ARIMA建模操作简单，只需进行几个参数的设置即可运行。特别地，SPSS软件对时间序列分析有强大的自动建模功能，即“专家建模器”，可以由软件自动生成模型，提高建模速度。

2.2.1 专家建模器建模

（1）导入原始数据并创建时间序列：将数据导入数据编辑器，设置痢疾病例数变量“x”（发病数）为数值变量，将时间变量“t”（日期）定义为日期和时间变量，设定为“年、月”，则建立时间序列｛Xt｝。

（2）专家自动建模：打开菜单项“分析”→“预测”→“创建模型”，在“时间序列建模器”选项卡中确定因变量x（发病数），在选项卡的“方法”选项中选择“专家建模器（仅限ARIMA模型）”，不需要设置具体参数。软件将自动计算，建立模型SARIMA(0,0,2)(1,0,0)12（表4）。

表4 备选模型的参数估计结果（SPSS）

2.2.2 模型识别与参数估计

建模的思路和操作步骤和SAS软件大致相同，只是调用菜单项来实现。

（1）模型识别

“分析”→“预测”→“序列图”，画出时间序列｛Xt｝以及差分、季节差分后的时序图，判断平稳性；“自相关”画出时间序列｛Xt｝的ACF和PACF图形，初步判断模型的阶数。

（2）参数估计和模型检验

“分析”→“预测”→“创建模型”，打开“时间序列建模器”选项卡，在选项卡的“方法”选项中选择“ARIMA模型”，输入自回归、差分和移动平均数的阶数（包括季节因子的阶数）。SPSS中没有自动识阶的功能，因此需要把所有可能阶数的组合都计算一遍，建立多个模型，对比它们的参数估计、拟合优度检验和残差白噪声检验等计算结果，选择“最优”模型。本例通过上述计算，筛选得到模型SARIMA(1,1,0)(0,1,1)12，其参数估计的各项结果符合“显著性”要求（P＜0.05）（表4）；模型拟合结果的标准化BIC值和MAPE最小，决定系数R2最大（表5）。残差白噪声检验中LB统计量P值都大于0.05，说明残差序列为白噪声序列。但专家建模结果SARIMA(0,0,2)(1,0,0)12的LB统计量值为57.36(P＜0.001)，显示不是白噪声序列，模型并不理想。

表5 备选模型的残差白噪声检验和拟合优度检验的结果（SPSS）

（3）模型预测

在上述的“时间序列建模器”选项卡，选择“拟合值”以及定义预测阶段，则可以计算预测值的点估计和区间估计，输出图形。此例中，两个模型各月的实测值都落在预测值95%置信区间内，但专家建模结果SARIMA(0,0,2)(1,0,0)12模型预测值的相对误差14.61%，预测精度差（表3）。

2.3 R软件

R软件提供了弹性、互动的环境分析和数据处理功能。它可以轻松地加载以库或者程序包的形式存在的补充工具，里面含有各种数学和统计计算的函数，以实现一些复杂的建模功能。在R中建立ARIMA模型，需先加载程序包FORECAST、TSERIES、TSA[4,7]，编程建模的思路和SAS基本相同：

（1）创建数据集

生成时间序列，定义为月度数据。

Xt=ts(c(353,411,…),start=c(2009/01),frequency=12)#建立时间序列｛Xt｝

（2）模型识别

绘制序列图，分析时序特性；根据ACF和PACF等结果对序列进行识别、定阶。R软件的程序包TSA中，armasubsets()函数有自动识阶功能，它根据最小BIC准则来挑选“最优”模型，结果具有参考价值。本例中自动识阶结果如下页图3，提示模型的阶数p=2，q=1。根据ACF和PACF图形特征，结合自动识阶的结果，可以设定阶数的取值范围，建立多个备选模型进行比较。

plot(Xt)#绘制序列图

acf(as.vector(Xt),lag.max=24)#序列自相关图ACF

pacf(as.vector(Xt),lag.max=24)#序列偏相关图PACF

resbic=armasubsets(y=Xt,nar=7,nma=7,ar.method='ols')#ARIMA模型自动识阶

plot(resbic)#不同ARIMA模型的BIC值

（3）参数估计

本例对阶数p≤2，q≤1，季节模型阶数P和Q不超过2的情形进行参数组合，建立SARIMA模型，通过（3）和（4）这两个步骤反复进行，比较备选模型的各项指标值，筛选得“最优”模型 SARIMA(1,1,0)(0,1,1)12：

m.Xt=arima(Xt,order=c(1,1,0),seasonal=list(order=c(0,1,1),period=12))#建立模型accuracy(m.Xt)#计算模型的各项拟合指标值

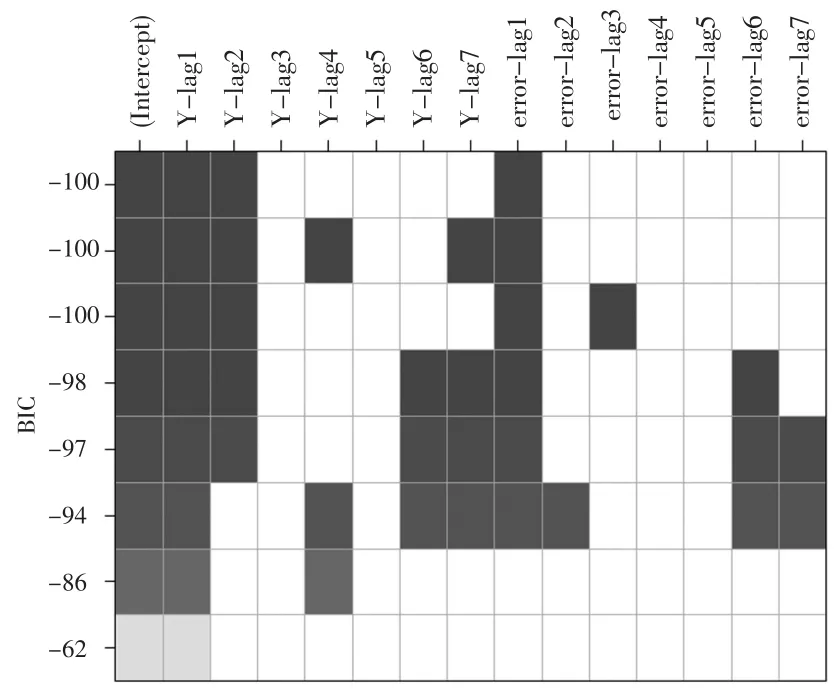
图3 不同p,q阶数建立的ARIMA模型的BIC值（R软件）

R软件的FORECAST程序包还提供了auto.arima（）函数，具有自动建模功能。本例中调用函数auto.arima(Xt)，得到最优模型SARIMA(1,1,0)(1,0,0)12及参数估计的结果（表6）。但R软件参数估计只提供系数和标准误，显著性检验需自行计算统计量t值（系数除以标准误的平方）来推断。通过计算，表6中两个备选模型的系数都符合“显著性”要求（P＜0.05）。

表6 备选模型的参数估计和模型检验结果（R软件）

（4）模型检验

R软件可以计算各延迟阶数的LB统计量及P值，并通过图形直观表达。从图4看出，上述两个模型的残差白噪声检验，P值均大于0.05，说明所建立模型的残差通过白噪声检验。各延迟阶数的LB统计量具体值也可以计算，如lag=18时，SARIMA(1,1,0)(0,1,1)12模型LB统计量16.405(P=0.5643)；自动建模SARIMA(1,1,0)(1,0,0)12模型LB统计量20.83(P=0.2882)。

BOX.test（m.Xt$residuals,lag=18,type=”Ljung-Box”）#计算LB统计量

tsdiag(m.Xt,gof=24,omit.initial=F)#LB统计量对应的P值图

图4 备选模型的残差白噪声检验（R软件）

（5）模型预测

预测指定时间范围序列｛Xt｝的值和置信区间，预测图形的绘制比较灵活、输出美观。图5是图形的输出，从具体预测值计算，拟合效果SARIMA(1,1,0)(0,1,1)12模型较好，MAPE为8.67%，自动建模SARIMA(1,1,0)(1,0,0)12模型预测精度较高，平均相对误差小，为6.64%（表3）。

图5 备选模型的预测值和置信区间（R软件）

2.4 EVIEWS建模

EVIEWS是广泛应用的计量经济学软件，能进行传统的时间序列分析，建立各种时序模型[3,10]。使用该软件可以采用编程建模和菜单过程步建模两种方式，本文以菜单功能实现说明ARIMA建模的步骤：

（1）导入数据

建立一个新的 Workfile，“File”→“Workfile Create”，在对话框输入起始日期与结束日期，新建时间序列，将案例中的数据导入，即可建立时间序列｛Xt｝。

（2）模型识别

自相关和偏自相关函数是识别模型的主要工具。先通过菜单项对时间序列｛Xt｝的时序特性进行识别，“View”→“Graph Option”，设置绘制序列对话框，绘制序列图、序列差分图等。再运行“Quick”→“Series Statistic”→“Correclogram”，得出序列的ACF和PACF等结果，可根据这些信息对序列模型进行识别、定阶，根据图6结果，初步判定p=1和q=1，P=1和Q=1。

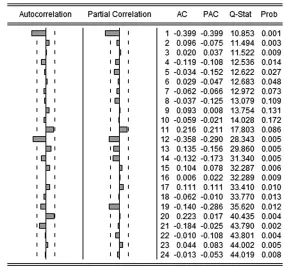
图6 差分后序列{∇∇12Xt}ACF和PACF结果（EVIEWS）

（3）参数估计

EVIEWS中参数估计采用非线性算法。建模过程为“Quick”→“Estimate Equation”，打开方程定义对话框，若拟建立的模型为SARIMA(1,1,0)(0,1,1)12，就输入相关的命令行：diffXt ar(1)ma(12)，就可得到结果输出(diffXt代表差分后序列{∇∇12Xt})。

图7 SARIMA(1,1,0)(0,1,1)12模型的参数估计结果（EVIEWS）

图7上半部分是参数估计系数及显著性结果，下半部分是模型拟合结果：R2=0.46，AIC=10.26，SC=10.32。

（4）模型检验

检验残差序列是否为白噪声，在方程输出窗口选择“views”→“Residual Tests”→“Correlogram-Q-Statistics”，在弹出的对话框中输入最大的滞后期lag=18，得LB统计量Q=18.940（P=0.27），其他延迟阶数LB统计量对应的P值都大于0.05，模型通过白噪声检验。

（5）模型预测

在方程输出窗口选择“forecast”，预测方法可以选择静态预测或追溯预测（Dynamic forecast），动态（向前多步）预测。得到拟合结果的MAPE为8.86%，Theil系数为0.047等结果（图8），预测值的平均相对误差为14.28%（表3）。

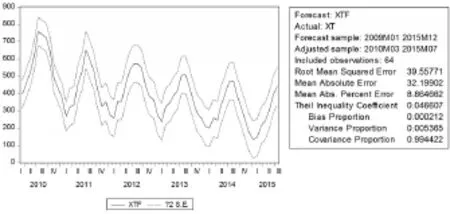
图8 ARIMA模型的预测和拟合结果（EVIEWS）

3 比较讨论

4种软件建模方法和应用中：SPSS操作过程最为简便，适合非专业统计建模的需求。其“专家建模器”操作简单，可以快速建模；运用菜单项建模也是“按部就班”，不需要复杂操作，有利于初学者使用；但算法呆板，灵活性差也是其不足之处。EVIEWS软件易学易用，输出整齐美观，是计量经济学常用的软件，但算法和功能不够全面有时会降低建模的精度。SAS软件提供很多命令和选项，建模功能强大，用户可以根据自己的需求灵活建模。但SAS输出不够美观，SAS编程有一定难度，需要应用者有一定编程基础。R软件是免费软件，建模灵活多变，目前的3.3.2版本已具有自动识阶、自动建模等多种功能；但R软件中会不断更新程序包，一方面使得建模功能越来越强大，另一方面也需应用者不断学习探索；也有一定的学习难度。

以上运用4种软件进行ARIMA建模，不同方法得到了不同的“最优”模型和预测结果。在本实例分析中，SARIMA(1,1,0)(0,1,1)12模型是编程得到的“最优”模型，拟合精度若以指标MAPE比较，R软件结果最佳；预测精度以预测平均相对误差比较，EVIEWS最差。这是因为建模过程中，不同软件提供或默认的算法不同，“最优”模型尽管形式相同，但参数估计的系数不同，拟合和预测的结果就略有差异。在软件自动建模方面，SPSS专家建模器得到的SARIMA(0,0,2)(1,0,0)12模型虽然参数估计结果均显著不为0，但残差白噪声检验未通过，因此拟合和预测效果都不理想。R软件自动建模得到的SARIMA(1,1,0)(1,0,0)12模型，在模型检验中各项指标AIC、BIC、MAPE等不是最优，但在此实例中预测精度最高（预测平均相对误差6.64%）（表3）。无论是SPSS还是R软件，自动建模的结果仅可做为参考。在编程建模时，结合ACF、PACF图和自动识阶结果，筛选“最优”模型，避免出现主观偏差。

总之，不同软件在ARIMA建模各有特色和优点，应用者可依据自身专业背景和建模需求选择不同的软件建立ARIMA模型。