基于小波分析的BP-SARIMA模型的CPI预测

彭乃驰，党 婷

（云南大学旅游文化学院 信息科学与技术系，云南 丽江 674199）

0 引言

建立合适的数学模型精准预测CPI对于相关部门制定宏观经济调控政策具有重要的参考意义。目前，在中国知网上可以检索到的CPI预测的文献高达130余篇，预测模型高达十余种，如神经网络、SARIMA、ARCH、VAR、GM等，但尚无公认的最优的预测模型。黄鹰翔[1]实证表明SARIMA能较好地预测CPI的变化情况。石春娟[2]通过实证说明了小波分解和ANFIS模型在CPI预测中的有效性。王宇等[3]利用BP神经网络对我国CPI进行预测，效果比较理想。本文以云南省CPI数据为例，利用小波分析去除CPI数据中的噪声，并在CPI预测中有较好效果的BP神经网络及SARIMA模型的基础上，建立小波分析的BP-SARIMA预测模型。本文通过对云南省1995年1月至2016年12月CPI的预测和检验，验证该模型在CPI预测中的有效性。

1 小波分析的BP-SARIMA模型

1.1 小波分析

小波分析的思想是用小波序列的迭加来逼近某一信号。小波分析在时间序列预测中的应用主要是基于小波分析中的多分辨率分析理论。多分辨率分析是通过改变伸缩及平移尺度得到信号的近似及细节部分，在不同分辨率下显示信号的特征，实现对信号不同时间尺度和空间局部特征的分析。采用小波方法可有效消除时间序列中的噪声[4]。小波分析实现的关键是小波函数及分解层数的选择，实际应用中可根据数据及不同小波函数的特点来选择。小波分析的过程可大体分为分解、去噪与重构三步。

设时间序列数据为 f(n)，则 f(n)的多分辨率分解可以表示为：

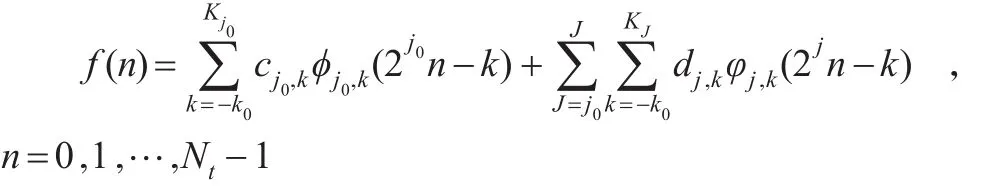
其中 ϕj0，k(2j0n-k)，φj，k(2jn-k)分别是尺度函数 ϕ(t)和母小波函数 φ(t)的伸缩和平移函数簇。 cj0，k，dj，k分别是在伸缩尺度 j0，j，平移尺度k上的展开系数。Nt是时间序列的点数。

1.2 BP神经网络

BP神经网络于1986年提出后，至今已在多方面广泛应用[5-7]。它是一种多层前馈神经网络，其特点是信号由输入层、隐层、到输出层前向传播，误差反向传播，并根据预测误差调整网络权值和阈值使预测输出不断逼近期望输出。

BP神经网络是一个3层感知器的数学模型。各层之间的数学关系如下：

对于隐层有：

对于输出层有：

上式中x0=-1是为隐层神经元引入阈值设置的，y0=-1是为输出神经元引入阈值设置的，一般情形下取

1.3 SARIMA模型

若时间序列{xt} 满足：H(LS)Δxt=Θ(LS)εt，则称{xt}为季节性SARIMA(P,D,Q)过程。SARIMA模型可用来描述具有周期性的非平稳的时间序列数据。SARIMA模型的表达式为：

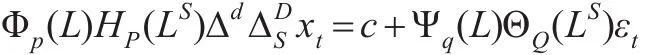
其中S为周期的长度，D为季节差分的阶数，P为季节自回归阶数，Q为季节滑动平均阶数，ΔS=1-LS为季节差分算子，

1.4 小波分析的BP-SARIMA模型的构建

本文以云南同比月度CPI为例，首先对原始数据作小波阈值去噪处理，再对去噪后数据作BP神经网络预测，最后通过SARIMA模型修正预测残差。按此思路结合小波分析、BP神经网络与SARIMA模型的优点，建立小波分析的BP-SARIMA模型。小波分析的BP-SARIMA模型的建模步骤为：

步骤1：选择某种小波及分解层数对CPI原始数据作分解。

步骤2：阈值处理，即设定某一阈值，只保留大于阈值的小波系数。

步骤3：用处理后的系数重构数据，得到去噪后的CPI数据。

步骤4：对去噪后的CPI数据再作相空间重构，将相空间重构后的数据分为训练数据与测试数据，并确定BP神经网络输入层神经元个数n与输出层神经元个数m。

步骤6：建立n-l-m结构的BP神经网络，多次运行网络，根据测试的MSE选择最优网络并运算出该网络的预测值。

步骤7：对BP神经网络预测相对于原始数据的残差作平稳性与季节性检验，若其存在季节性则可建立SARIMA模型。

步骤8：在残差符合建立SARIMA模型的条件下，进一步确定SARIMA模型的参数(p，d，q)×(P，D，Q)s，从而建立SARIMA(p，d，q)×(P，D，Q)s模型并对残差作预测。

步骤9：将BP神经网络的预测结果与SARIMA模型的预测结果相加即得小波分析的BP-SARIMA模型的预测结果。

步骤10：通过平均相对误差、均方误差等标准测试建立的小波分析的BP-SARIMA模型，测试效果较好则该模型可用于CPI预测。

2 实证

2.1 数据来源

本文选择云南省1995年1月至2016年12月的CPI同比月度数据，数据量共264个，数据来源于国家统计局网站。原始数据（记为X）的时序图见图1。从图1可见，1995年的云南月度CPI处于同比增长率在20%左右的高位上，消费者物价处于严重的通货膨胀阶段。1995—2000年底，云南月度CPI经历长达六年的递减后，CPI达到了增长率-3%左右的历史最低值。随后云南CPI又经历了长期的波动性增长，并于2004年与2008年两次达到了增长率9%左右的峰值。2014—2016年，云南的同比月度CPI基本控制在增长率1%～3%之间，处于较理想的状态。将云南CPI数据划分为1995年1月至2015年12月与2016年1月至2016年12月两部分，前者用于建立模型，后者留作对模型的预测效果作测试。

图1 云南CPI原始数据

2.2 数据的小波阈值去噪

云南CPI同比月度数据不可避免地会受到某些扰动项的影响，在采集到的数据中会包含一定的噪声，这些噪声不能反映数据的本质特征，对预测结果会存在一定的干扰。因此，为提高预测精度可先对CPI原始数据作小波阈值去噪处理。

目前，对小波函数的选择尚未有统一方法，由于Haar小波（即db1小波）具有正交性、紧支撑性与对称性，故选择该小波。小波分解的层数过少会使去噪后的数据平滑性和平稳性较差，分解的层数过多又会使分解过程中产生的计算误差较大，综合考虑这两方面后选择三层小波分解。选定db1小波三层分解后，使用MATLAB软件中的小波工具箱，采用默认阈值重构法，完成对CPI原始数据的小波阈值去噪。去噪后的云南CPI数据记为S，其时序图如图2所示。

图2 去噪后的云南CPI

2.3 去噪后数据的BP预测

将去噪后的云南CPI数据S首先作相空间重构，经多次试验确定出最小嵌入维为3，时间延时为1，即用前三个月的CPI预测下一个月的CPI。经相空间重构后的数据形式如表1所示：

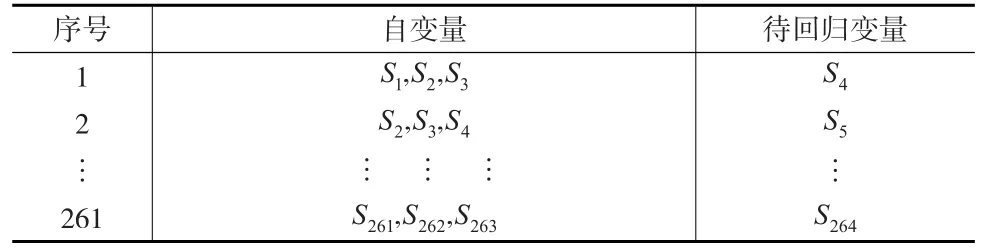
表1 相空间重构数据形式

其中，Si为S的第i期数据。为了与前文建模数据与测试数据的划分一致，取表1中1～249号数据对BP模型的网络作训练，用于建立BP神经网络模型，而250～261号数据作为测试数据，不参与模型建立。

相空间重构完毕后就确定了BP神经网络的输入层神经元个数n=3，输出层神经元个数m=1，代入经验公式得即初步确定出隐层神经元个数的取值范围为3至12的整数。因为BP神经网络训练出来的模型每次都不一致，故隐层神经元个数依次取3，4，…，12各重复建模10次，分别计算出测试均方差MSE的10次平均值，通过比较取隐层神经元个数为3，建立3－3－1结构的BP神经网络。反复训练3－3－1结构的BP神经网络，记录每次的测试均方差，从中找到一个测试效果最好的网络并保存。利用该网络建立的BP模型，产生拟合期的预测值Yi(i=4，5，…，252)与测试期的预测值Yi(i=253，…，264)，并计算出其相对于原始数据X的残差 Ei=Xi-Yi(i=4，5，…，264)。以上BP预测过程通过调用MATLAB软件中的神经网络工具箱函数实现。为了提高预测精度，拟合期的残差Ei(i=4，5，…，252)用于进一步建立SARIMA模型。BP模型的预测值 Y及残差E的图像分别如图3和图4所示。

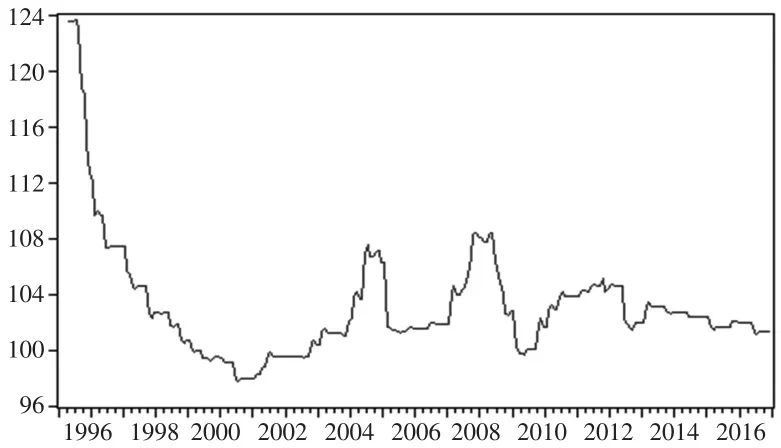
图3 BP预测值

图4 BP预测残差

2.4 BP预测残差的SARIMA预测

对BP模型拟合期的预测残差序列E作无截距、无趋势的ADF单位根检验，t统计量为-10.19小于显著性水平1%下的临界值-2.57，认为残差序列E为平稳序列，故序列E无需作差分。作E的相关图，如图5所示。从图5可见，当滞后期k=12时，自相关与偏自相关系数明显超出置信带，显著不为0，这表明序列E存在季节性。为消除季节性，对序列E作步长为s=12的季节差分产生序列SE，再对SE作无截距、无趋势的ADF单位根检验，t=-6.83＜-2.57，表明SE仍为平稳序列，符合SARIMA模型的建模条件，可建立 SARIMA(p，d，q)×(P，D，Q)s模型。

图5 BP预测残差E相关图

由于序列E平稳，取d=0；作一阶季节差分后季节性大体消除，取D=1；图5中当k=12时自相关与偏自样系数显著不为0，取P=Q=1。SE的相关图（见图6）中偏自关系数与自相关系数分别在滞后2阶与1阶后多数处于置信带内，为了使模型预测效果更准确，适当扩宽 p，q的取值范围，取 p=1，2，3与 q=0，1，2 为待选阶数。综上所述，建立的待选模型为 SARIMA(p，0，q)×(1，1，1)12（ p=1，2，3，q=0，1，2），共有九个模型。依据调整 R2、AIC准则、SC准则选择模型，其中调整R2大优，AIC与SC小优。九个待选SARIMA模型的检验结果见表2。

图6 SE相关图

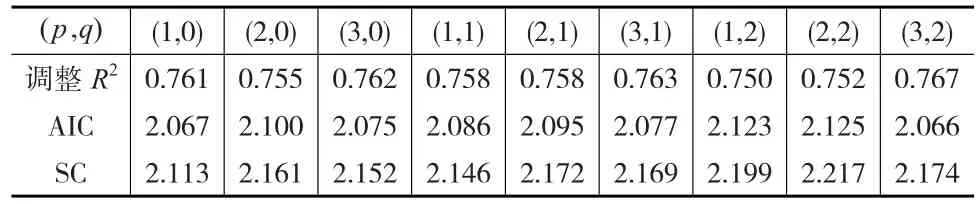
表2 SARIMA模型检验结果

由表2可见 SARIMA(1，0，0)×(1，1，1)12与 SARIMA(3，0，2)×(1，1，1)12两模型的AIC都很小且几乎相等，前者的SC最优，后者的调整R2最优，故先排除其余七个模型，从这两个模型中作选择。考虑到 SARIMA(1，0，0)×(1，1，1)12模型的各项系数的估计值在1%水平下都显著，另一模型有两项系数的估计值不显著（5%水平）,且 SARIMA(1，0，0)×(1，1，1)12模型的残差通过白噪声检验，最终选择该模型，其表达式为：

(1-L12)(1-0.449L)(1+0.450L12)Et=(1+0.935L12)εt

利用 SARIMA(1，0，0)×(1，1，1)12模型对序列 E 作静态滚动预测，得拟合期的预测值 Ei(i=29，…，252)与测试期的预测值 Ei(i=253，…，264)。

2.5 结果分析

表3 模型测试效果对比

由表3可见，三个模型的各期测试相对误差都控制在0.7%之内，测试效果均比较理想，它们都可用于对云南同比月度CPI作预测。在这三个模型中，小波分析的BP-SARIMA模型平均相对误差与均方误差都最小，为最优模型。小波分析的BP-SARIMA模型相对未经小波分析的BP-SARIMA模型，测试期的平均相对误差与均方误差各减少了0.06%及0.044。小波分析的BP-SARIMA模型相对未经SARIMA残差修正的小波分析的BP模型，测试期的平均相对误差与均方误差各减少了0.031%及0.021。

3 结论

对小波分析的BP-SARIMA模型的主要研究结论如下：（1）该模型测试期的平均相对误差为0.239%，均方误差为0.091，预测精度高，可用于对CPI作预测研究；（2）通过与未经小波分析的BP-SARIMA模型及未经SARIMA残差修正的小波分析的BP模型作对比，该模型的预测精度更高，测试期的平均相对误差与均方误差都有明显下降。进一步的研究方向：（1）该模型的改进。比如将BP神经网络换成其他类型的神经网络（RBF神经网络、模糊神经网络等），模型预测精度是否会有提高。（2）该模型是否适合其他类型经济指标的预测，比如GDP等。