含粘弹性层纤维增强层合板的热屈曲及阻尼特性分析
马卓瑞,李金强,2,冯 伟
(1.太原理工大学 力学学院,太原 030024;2.超达阀门集团股份有限公司,浙江 温州 325000;3.中车齐齐哈尔车辆有限公司,黑龙江 齐齐哈尔 161000)
相较于传统金属材料,纤维增强复合材料质轻、耐腐蚀、比刚度大、比强度大、可设计性强,现广泛应用于航空航天、潜艇、桥梁以及建筑等领域。在实际应用中这些结构可能遭受恶劣环境载荷作用,比如飞行器在太空受到辐射,温度发生显著变化,产生的热膨胀以及边界约束使结构内部产生压应力,从而可能造成热屈曲。因此有必要对层合板在不同温度场中的热屈曲行为进行研究[1-5]。
TAUCHERT[6]对中厚反对称角铺设层合板在简支边界条件和均匀升温下进行了热屈曲研究,并分析了纤维取向、板层数、板厚度和长宽比对临界屈曲温度的影响。基于经典层合理论和伽辽金法,CHEN et al[7]研究了均匀温度场下反对称角铺设层压板的热屈曲。SHIAU et al[8]使用有限单元法研究了层合板的热屈曲行为,并详细分析了具有不同E1/E2、长宽比、纤维方向、铺层顺序以及边界条件的正交铺层和角铺层合板的热屈曲模态。MORADI et al[9]使用差分正交法研究了均匀温度场下矩形层合板受任意边界条件约束的热屈曲行为。OUNIS et al[10]研究了层合板在均匀温度场下的热屈曲行为,发现临界屈曲温度通常随着模量比EL/ET和热膨胀比αT/αL的增加而降低,且受边界条件和纤维取向的影响很大。
在实际应用中,层合板经常受到非均匀温度场的影响。近来,层合板在非均匀温度场下热屈曲等力学性能的研究引起了广泛关注[11-15]。CHEN et al[11]在考虑横向剪切变形和旋转惯性的情况下,使用热弹性Mindlin板理论和有限元法分析了均匀和不均匀温度场下层合板的热屈曲性能。GHOMSHEI et al[12]采用差分正交法(DQM),分析了在均匀和非均匀温度场下对称正交矩形层合薄板的热屈曲行为。LI et al[13]研究了非均匀温度场和局部分布各向异性对层合板热屈曲的影响。结果表明,不均匀热负荷影响板的正交各向异性属性。田新鹏等[14]对层合板在均匀温度场和非均匀温度场下的热屈曲行为进行了研究,发现临界热屈曲温度与其边界条件以及热源位置密切相关。SONG et al[15]分析了超声速气流中非均匀温度分布的非线性层合板的气弹性问题。
先前的研究工作多集中在各向同性与各向异性层合板的热屈曲,对含粘弹性层层合板热屈曲行为的分析较少。粘弹性材料由于其兼有粘性和弹性,对粘弹性层合板的屈曲行为有显著影响[16-17],且可作为阻尼材料使结构能量耗散。故本文考虑在层合板中嵌入粘弹性层,并采用经典冯·卡门平板理论和哈密顿原理推导得出含粘弹性层纤维增强层合板的运动学方程,然后得出临界热屈曲温度的求解公式以及结构固有频率和阻尼比等。计算了结构临界热屈曲温度随粘弹性层厚度以及铺设角度的变化,并计算了恒温下固有频率和阻尼比随粘弹性层厚度以及铺设角度的变化。重点研究了非均匀温度分布对结构临界热屈曲温度、固有频率和阻尼比的影响。由此对含粘弹性层纤维增强层合板的热屈曲及阻尼特性进行分析研究。
1 复合材料层合板热本构方程
含粘弹性层纤维增强层合板模型如图1所示,为对称层合板,其中中间两层为粘弹性层。板的长、宽、高分别为a,b,h,取层合板中面为x-y坐标平面,z轴垂直于x-y坐标平面。坐标原点位于层合板中面中心。
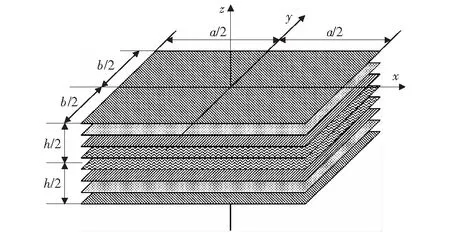
图1 含粘弹性层纤维增强层合板Fig.1 Fiber reinforced laminated composite panels with viscoelastic layers
由冯·卡门经典平板理论,可得层合板任一点(x,y,z)应变-位移关系:
{ε}={εm}+z{κ} .
(1)
式中:εm是膜应变向量;κ是弯曲曲率向量。它们可由振动位移表示:

(2)
式中:u,v和w表示位移分量,分别对应坐标轴的3个轴向且都为多项式。
合力矢量{N}={NxNyNxy}和合力矩矢量{M}={MxMyMxy}可写成下式:
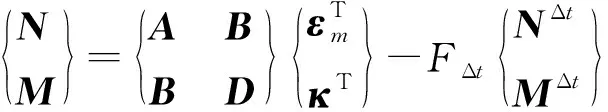
(3)
式中:FΔt是温度函数,可表示为:
FΔt=Δtf(x,y,z) .
(4)
式中:Δt是温差幅值,而f(x,y,z)则表示温度分布函数。例如,均匀温度分布为f(x,y,z)=1.
式(3)中,A,B和D指的是拉伸刚度矩阵、拉伸-弯曲耦合刚度矩阵和弯曲刚度矩阵,可表示为:
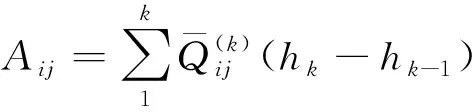

i,j=1,2,6 .
(5)
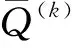
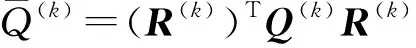
(6)
式中,R(k)和Q(k)分别表示为:
R(k)=
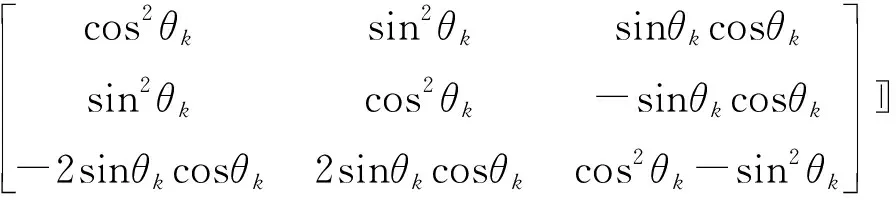
(7)
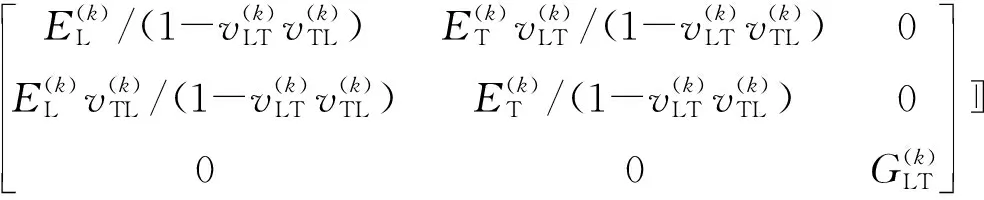
(8)
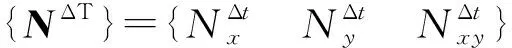

(9)

(10)
纤维增强层合板的总应变能U和总动能T可表示为:
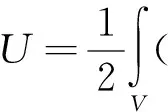
(11)

(12)
式中,V和ρ表示层合板的体积和密度。
由哈密顿原理:

(13)
得到层合板的运动方程为:
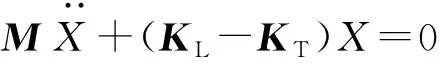
(14)
式中:M,KL和KT分别为系统的总质量矩阵、刚度矩阵和温度刚度矩阵。
2 热屈曲及阻尼特性分析
随着温差的不断增加,层合板的固有频率降低。当其值为零时,板发生屈曲,此时与常温相比的温度变化量Δtcr即为临界热屈曲温度。如果温度分布函数f(x,y,z)是一定的,可由下式求解临界热屈曲温度Δtcr[13]:
(KL-λKT)X=0 .
(15)
临界热屈曲温度Δtcr可由最小的特征值λ0和初始值Δt0表示:
Δtcr=λ0Δt0.
(16)
式(14)的通解为[18]
X(t)=X0eλt.
(17)
式中:X0和λ分别为系统的特征向量和特征值;t表示时间。而特征值λ可表示为:
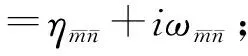
(18)

(19)
3 数值算例
3.1 计算方法验证
为验证本文方法的正确性,对文献[14]中算例进行模拟,其各项参数为:横向弹性模量ET=8.07 GPa,纵向弹性模量EL=155 GPa,剪切弹性模量GLT=4.55 GPa,泊松比μLT=0.22,密度ρ=1 600 kg/m3,纵向热膨胀系数αL=0.07×10-6/℃,横向热膨胀系数αT=30.1×10-6/℃.几何尺寸a=b=100h,铺设角度为[0/0/0/0]s.计算结果如表1所示。通过与文献[14]结果以及ANSYS结果比较可以发现,采用本文方法计算的结果与文献结果和ANSYS结果都符合良好,由此说明本文计算方法正确。
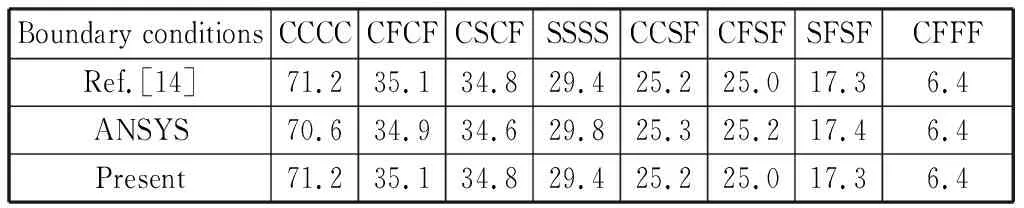
表1 不同边界条件下含粘弹性层纤维增强层合板的临界屈曲温度Table 1 Critical buckling temperature of fiber reinforced laminated composite panels with viscoelastic layers under different boundary conditions ℃
3.2 粘弹性层厚度对层合板热屈曲及阻尼比的影响
含粘弹性层纤维增强层合板中纤维层的各项参数为:横向弹性模量ET=8.07 GPa,纵向弹性模量EL=155 GPa,剪切弹性模量GLT=4.55 GPa,泊松比μLT=0.22,密度ρ=1 600 kg/m3,纵向热膨胀系数αL=0.07×10-6/℃,横向热膨胀系数αT=30.1×10-6/℃.粘弹性层参数由文献[19]给出:密度ρv=1 100 kg/m3,Q11v=Q22v=78.42(1+i)MPa,Q12v=38.43(1+i)MPa,Q66v=20(1+i)MPa,热膨胀系数取α=0.02×10-6/℃.层合板的几何尺寸:a=1.25 m,b=1 m,h=0.004 m.边界条件为四边简支,铺设角度为[0/90/90/粘]s.
对均匀温度场及非均匀温度场下的临界屈曲温度进行计算,其中非均匀温度场采用函数为F(x,y)=Δt×2×(a/2+x)/a的简单线性温度场(保证均匀温度场与非均匀温度场下整个层合板的温度变化相同)。图2给出了临界热屈曲温度随粘弹性层厚度的变化曲线。由图2可知,不论均匀温度场还是非均匀温度场,层合板中粘弹性层厚度越大,临界热屈曲温度也越来越大,且基本呈现正比例关系。但在均匀温度场下临界热屈曲温度随粘弹性层厚度变化较快。由图3给出的恒温下固有频率和阻尼比随粘弹性层厚度的变化曲线可以看出,恒温下阻尼比随粘弹性层厚度的增加而增大,且近似线性。固有频率随粘弹性层厚度的增加而减小,但总体影响较小。由此可见,在层合板中加入粘弹性层,并调节粘弹性层的厚度,不仅可获得期望的临界屈曲温度,还可以降低振动的振幅,尤其是共振区附近的振幅,使结构在共振频率附近工作成为可能。
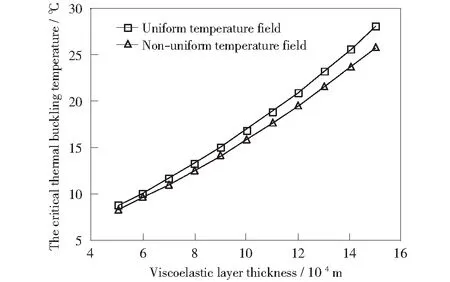
图2 临界热屈曲温度随粘弹性层厚度的变化曲线Fig.2 Variation of the critical thermal buckling temperature with the thickness of the viscoelastic layer
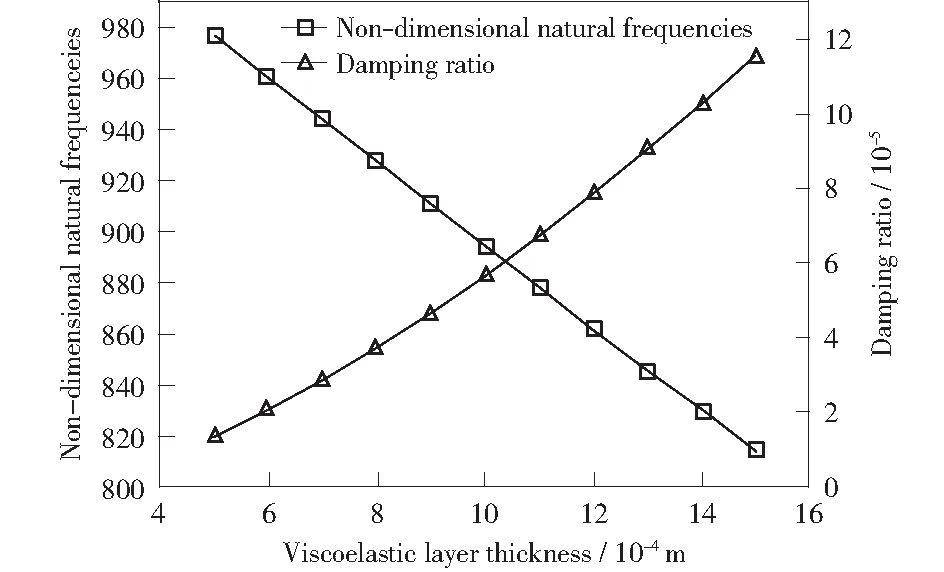
图3 恒温下固有频率和阻尼比随粘弹性层厚度的变化曲线Fig.3 Variation of non-dimensional natural frequencies and damping ratio with the thickness of the viscoelastic layer under constant temperature
3.3 铺设方式对层合板热屈曲及阻尼比的影响
在非均匀温度场下(同上),分析了在两种典型的铺设方式[0/a/0/粘]s和[a/a/a/粘]s的情况下层合板的热屈曲问题。表2给出了不同铺设方式层合板的临界热屈曲温度。可以看出,[0/a/0/粘]s较[a/a/a/粘]s铺设方式的层合板临界热屈曲温度高。不论是[a/a/a/粘]s还是[0/a/0/粘]s铺设方式,随着a的增大,层合板的临界热屈曲温度都会先增大。当a达到某一值时,[a/a/a/粘]s板的临界热屈曲温度会达到最大值,然后迅速减小,而[0/a/0/粘]s板的临界热屈曲温度几乎不受a变化的影响。
然后在恒温下分析了不同铺设方式对层合板固有频率和阻尼比的影响。表3给出了恒温下不同铺设方式层合板的固有频率和阻尼比。由表3可知,一般情况下,[0/a/0/粘]s较[a/a/a/粘]s铺设方式的层合板阻尼比小,当a较大时[0/a/0/粘]s板阻尼比反而比较大。[0/a/0/粘]s板的阻尼比随着a的增大而减小。而[a/a/a/粘]s板的阻尼比随着a的增大先增大后减小,会出现一个峰值。与阻尼比变化规律类似,[0/a/0/粘]s较[a/a/a/粘]s铺设方式的层合板的固有频率小,但[0/a/0/粘]s板的固有频率随着a的增大先增大后减小,而[a/a/a/粘]s板的固有频率一直增大。

表2 非均匀温度场下不同铺设方式的临界热屈曲温度Table 2 Critical thermal buckling temperature of different paving patterns under non-uniform temperature field

表3 恒温下不同铺设方式的固有频率和阻尼比Table 3 Non-dimensional natural frequencies and damping ratio of different paving patterns under constant temperature
3.4 非均匀温度分布对层合板热屈曲及阻尼比的影响
本节采用4种温度分布函数研究非均匀温度分布对层合板热屈曲及阻尼比的影响,并确保每种温度分布函数下整个层合板温度变化是一定的,其中不同颜色对应的温度由公式得出,4种温度分布函数及其温度分布图如下:
1) 热源在角点。
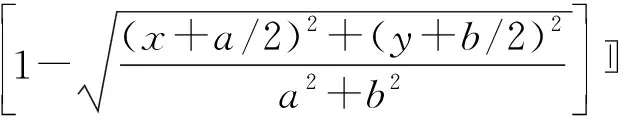
2) 热源在中心点。
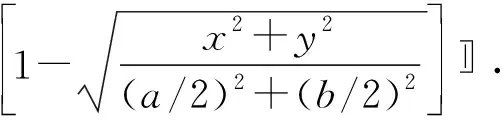
3) 热源在右边界。
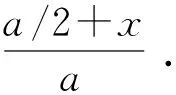
4) 热源在上边界。
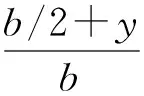
其中,a1,a2,a3,a4都是常数。
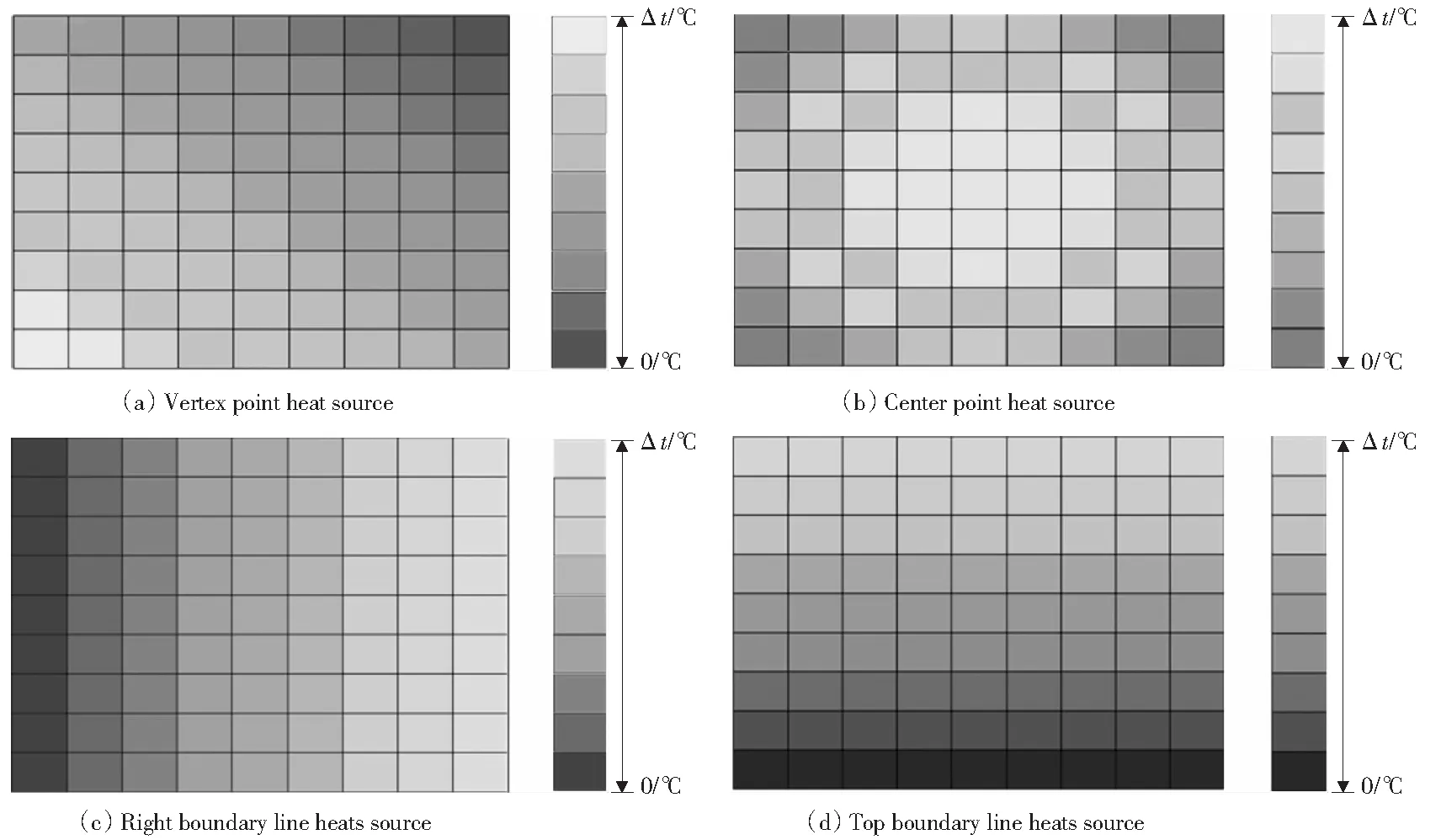
图4 不同热源下层合板的温度分布图Fig.4 Temperature distributions under different heat sources
图5给出了4种温度分布函数下固有频率随温差的变化曲线。随温差的增大,固有频率均降低。相同温差下,热源位于层合板的中心点,固有频率最高。热源位于层合板的右边界,固有频率最低。热源分别位于层合板的角点、中心点、右边界以及上边界时,其对应临界热屈曲温度分别是8.837 2,10.187 0,8.248 0,8.621 9 ℃.由此可以看出,即使层合板温度变化一定,当层合板上的温度分布不同时,临界热屈曲温度、固有频率也明显不同;且热源离板的中心越近,层合板临界热屈曲温度、固有频率越高。这是由于对于四边简支含粘弹性层层合板,其中心对温度变化反应更不敏感。
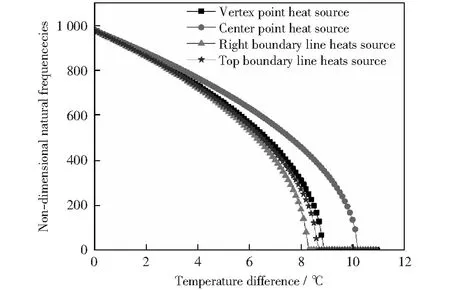
图5 不同温度分布函数下固有频率随温差的变化曲线Fig.5 Variation of non-dimensional natural frequencies with temperature difference under different temperature distribution functions
图6给出了不同温度分布函数下阻尼比随温差的变化曲线。可以看出,随温差的增大,阻尼比均升高;在同一温差下,热源位于层合板的右边界,阻尼比最高;热源位于层合板的中心点,阻尼比最低。即热源离板的中心越近,阻尼比越低。这与非均匀温度场分布对固有频率的影响正好相反。

图6 不同温度分布函数下阻尼比随温差的变化曲线Fig.6 Variation of damping ratio with temperature difference under different temperature distribution functions
4 结论
1) 不论均匀温度场还是非均匀温度场,弹性层总厚度一定的情况下,层合板临界热屈曲温度随粘弹性层厚度增大而增大,且基本呈现正比例关系。恒温时,层合板阻尼比随粘弹性层厚度增大而增大,固有频率随粘弹性层厚度的增加而减小,但总体影响较小。
2) 临界热屈曲温度、固有频率、阻尼比除了受纤维铺层影响较大外,也与层合板上的温度分布有关。如对于本文中的四边简支含粘弹性层层合板,热源离板的中心越近,层合板临界热屈曲温度和固有频率越高,阻尼比越低。

