考虑绿证-碳交易机制的含风电电力系统优化调度

薛英杰，赵书强，张 现，陈家玉，刘仕豪

(华北电力大学 电力工程系，河北 保定 071003)

在全球环境日益恶化，化石类能源日益枯竭的情况下，风能作为一种清洁、安全的可再生能源，得到迅猛发展。据国家能源局发布数据显示，到2017年上半年，全国风电累计并网装机容量已达到1.54亿kW，发电量为1 490亿kW·h，累计装机容量与发电量均居世界首位。但是风电的不确定性、波动性及反调峰特性严重制约着自身发展，上半年弃风电量为235亿kW·h，弃风率仍高达15.8%[1]。为减少温室气体排放，鼓励可再生能源发展，提高可再生能源发电在一次能源消费中所占比例，我国先后制定了碳排放交易机制与绿色交易证书机制，并于2017年7月1日开展证书的认购工作[2]。

国内外学者对碳交易已做了深入研究，其中碳交易主要应用在系统调度与规划方面。文献[3]基于总额度约束的排放轨迹，建立了低碳经济下基于排放轨迹约束的电力系统电源扩展规划模型；文献[4-5]在电网调度中引入碳排放成本，即实际的碳排放量大于分配限制时则需购买碳排放权，小于时则盈利，使碳排放成为赋有经济价值的可调度资源，但在碳排放权管理方面并未规范具体要求；文献[6]在碳排放成本中引入高额罚金，从而进一步限制了发电系统的CO2排放，提高了风电等新能源的发电权。以上文献在搭建碳交易模型时均未考虑碳抵消机制从而使模型结果与实际存在较大偏差。关于绿证交易机制的研究主要集中在电力市场侧，通过对机制内容不断补充来影响电力市场侧行为，缺乏对绿证交易机制的量化建模。文献[7]以可再生能源配额制为背景，引入绿色证书交易概念并针对当前可再生能源产业发展的一些弊端阐述了绿色证书带来的积极作用，对绿证交易机制的具体模型并未提及；文献[8-9]给出绿证推广的国际经验，提出“市场电价+绿证收入”盈利模式；文献[10]针对可再生能源配额制下的绿色证书交易机制，设计出一个激励相容的双边拍卖机制，促进了具有成本优势的可再生能源发展。目前涉及碳交易调度的文献一般仅考虑了碳交易中碳分配额成本，对碳分配额进行买卖并综合火电机组出力来计算碳交易成本，并未考虑碳抵消机制对总成本的波动；有关绿证交易的文献很少涉及将绿证交易量化处理，对绿证交易机制与碳交易机制结合影响并未做细致研究。故本文综合考虑包含碳抵消模式的碳交易机制与绿色证交易机制，建立绿证-碳交易模型，通过TCC成本对其量化处理。

本文构建综合考虑绿证-碳交易机制的含风电电力系统优化调度模型，在经济目标函数中引入TGC成本与考虑碳抵消模式的CT成本。通过调控风电比例来控制TGC成本，将TGC成本模型分为三段函数处理；TGC机制通过单位供电强度来影响CT模型中实际碳排放量实现结合影响；引入碳抵消额成本，碳交易采用总量控制方式，基于地区电网基准线排放因子确定机组的分配额度，将碳交易模型分为三段函数计算；基于机会约束理论处理风电预测误差的不确定性，采用布谷鸟算法处理目标函数，从而实现含风电电力系统优化调度。

1 TCC成本模型

TCC成本是新电改能源政策在发电侧的具体体现，由TGC成本与CT成本构成，单位供电CO2排放强度实现TGC与CT一体连接。

1.1 TGC成本模型

绿色证书交易机制是配合可再生能源配额制顺利实施的辅助政策，由专门机构对特定的可再生能源发电量进行认证，发放具有可再生能源电量标识的可交易的证书[11]。本文可再生能源考虑风力发电，取一天24个点进行风电出力预测，每个点的预测出力值以及每个点的火电出力值规定为这1 h内风火出力的平均值。

TGC成本模型第一阶段为实际可再生能源发电比例大于规定配额比例，出售可再生能源产生的电量(反映在模型上以出售绿证形式表示)获利阶段；第二阶段为实际可再生能源发电比例小于规定配额比例，但仍在惩罚裕度内，此时只需对不足可再生能源发电量以绿证形式进行购买；第三阶段为实际可再生能源发电比例严重不足，超出惩罚裕度，此时不仅需要对可再生能源电量进行购买，还需要接受惩罚机制，具体计算公式见式(1).

f1=

(1)

式中：f1为TGC成本；k为发改委规定的可再生能源发电量占总上网电量的配额比例，满足k≥15%；u为实际可再生能源占上网电量的比例；s为惩罚裕度，模型中表示为可再生能源占总体上网电量的裕度百分比；cp为惩罚价格；c为风电绿证交易价格，参考绿证认购平台2017年7月份线上交易情况，Pa，Pw和PG分别为单位时段内发电厂的上网电量、风电上网电量和火电上网电量；具体计算公式见下式：

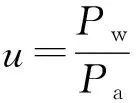
(2)

Pa=PG+Pw.

(3)

每一部分可再生能源发电量减少的CO2排放量是由火电机组决定的确定值。计算公式见下式：

Cc=Z'Pw.

(4)

式中：Cc为可再生能源发电间接减少的CO2排放量；Z'为单位供电排放强度，单位kg/MWh.可再生能源发电量直接影响TGC成本，故本文利用算例参数计算单独考虑TGC机制的机组出力值，并与传统调度机组出力值比较，Z'的值由测量时段内出力最大变化机组决定。

1.2 CT成本模型

1.2.1 碳分配额模型

碳分配额有免费和有偿分配两种方式。我国碳交易处于起步阶段，大部分碳交易额度以免费分配的方式分配给电厂，故本文采用基于发电量的免费初始分配方式。其分配方法主要有基准线和历史法两种，北京与湖北等地采用基准线法，深圳采用历史法进行分配。本文采用基准线法进行初始分摊碳分配额度，以一个含风电场的发电公司为例，t时刻分摊得到的碳分配额为：

CDt=ηPDt.

(5)

式中：CDt为t时刻系统分配得到的碳分配额，kg；PDt为t时刻的负荷预测值，MW；η为国家发改委规定的区域单位电量碳分配额分配系数，kg/MW.

1.2.2 碳抵消额模型

我国目前用于碳抵消的项目类型以碳抵消信用(CCER)为主。CCER是指经国家自愿减排管理机构签发的减排量，已成为国内市场碳抵消机制的主要交易对象。碳抵消机制主要体现在允许减排主体在履行年度碳排放控制责任时，可以采用相应的经过认证的其他减排量来抵消一定比例的减排量[12]，即允许使用CCER抵消一定比例的碳排放，从而使碳交易市场活跃化。碳抵消额满足一定的约束即：

0≤Cot≤0.05CDt.

(6)

式中：CDt为t时刻发电集团通过CCER核证得到的碳抵消额。

1.2.3 碳交易成本模型建立

碳交易成本模型包括3个阶段：当实际碳排放量在碳配额以内，出售多余的碳分配额和全部的碳抵消额进而获利；碳实际排放量大于碳分配额但小于碳分配额与碳抵消额之和时，出售多余的碳抵消额；碳实际排放量大于碳分配额与抵消额之和时，从碳交易市场购买碳量。综合考虑市场交易价格中，碳抵消额价格普遍低于碳分配额价格，故本文采用需要购买的碳额度为碳抵消额，且购买量充足(即可以购买到足够的碳抵消额)。碳交易成本的计算公式如下：

Fqt=

(7)

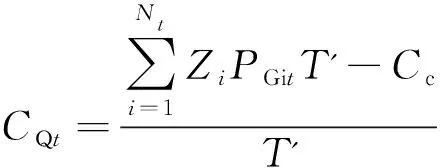
(8)

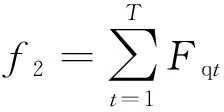
(9)

式中：Fqt为t时刻系统的碳交易成本；CQt为t时刻的系统碳实际排放量；Zi为第i台机组的碳排放强度；KDst和KOst分别为t时刻碳分配额和碳抵消额的卖出价格；KObt为t时刻碳抵消额的买入价格；PGit为t时间段内第i个常规机组计划出力；Nt为常规机组数量；f2为系统碳交易成本；T为调度时段，取24 h；T'为单位测量时段，取1 h.

TCC成本为TGC成本与CT成本之和，具体见式(10)

f3=f1+f2.

(10)

式中：f1为TGC成本；f2为CT成本；f3为TCC成本。

2 含风电场优化调度模型

2.1 火电机组经济成本

火电机组发电运行成本包括煤耗成本与考虑阈点效应成本，具体为：

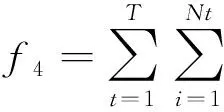
(11)

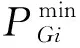
2.2 弃风成本

(12)

式中：f5为系统弃风成本；Kt为风电机组在t时刻的弃风容量价格；Pwst为风电机组在t时刻的调度出力。

2.3 购买备用成本

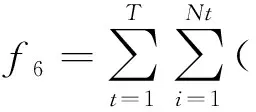
(13)

式中：Uit，Dit分别为机组i在t时刻正、负旋转备用，λi，πi分别为单位正、负备用容量价格。

本文经济调度目标函数为TCC成本、火电机组运行成本、弃风成本与购买备用成本之和最小，下见式：

min(f)=f3+f4+f5+f6.

(14)

2.4 系统约束条件

2.4.1 功率平衡约束

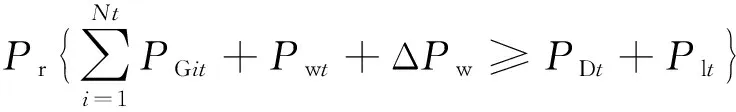
(15)

式中：Pr为事件成立的概率；PDt为t时段内负荷需求；PLt为t时段电力的传输损耗；ΔPw为风电出力误差；η1为满足负荷需求的置信水平。

考虑电力线路容量的约束，采用直流法计算线路潮流。基于Kron损耗方程[13]，传输损耗在各时间段内的传输损耗简化方程表示为:

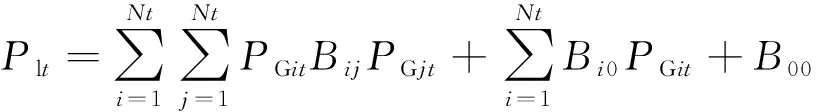
(16)

式中：Bij,Bi0和B00是电力网功率损耗矩阵B中的损耗系数，其中第2和3项数值较小，本文中不考虑。

2.4.2 火电机组出力约束

(17)

2.4.3 旋转备用约束

旋转备用约束是用来应对风电预测误差引起的火电机组出力的波动性。

(18)

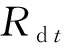
2.4.4 机组爬坡约束

-tr·rid≤PGit-PGi(t-1)≤tr·riu.

(19)

2.4.5 可再生能源发电配额比例约束

k≥15% .

(20)

2.4.6 碳交易抵消额约束

0≤Cot≤0.05CDt.

(21)

2.5 风电场出力与负荷随机性

采用beta分布拟合[14-15]基于某一风电预测水平的风电短期出力概率分布模型，其概率密度函数见式(22).

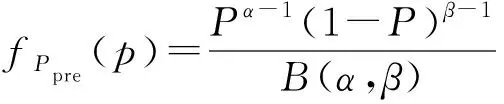
(22)

式中：P为归一化风电功率，由风电场实际功率P确定，见式(23)，其中Pmin和Pmax分别为风电场最小和最大出力值；B(α,β)为归一化系数，α，β由归一化后风电功率预测值Ppre和预测方差δ2决定，其公式见式(24)-(27).

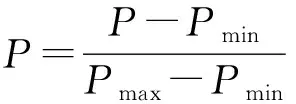
(23)

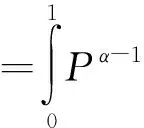
(24)

(25)

(26)

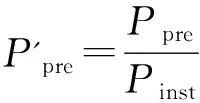
(27)

式中：Pinst为风电装机总量。

采用服从正态分布的预测误差随机变量表示系统负荷的随机特性，见式(28).

PDt=PDt'+ΔPDt.

(28)

式中：PDt和PDt'分别为负荷实际值与预测值；ΔPDt为负荷预测误差，服从均值为0、标准差为δLj的正态分布。

2.6 随机约束的处理

采用机会约束规划将随机约束转化为确定性约束进行求解，其显著特点是随机约束条件至少以一定的置信水平成立。根据机会约束理论[16]，随机约束函数由以下公式转化成确定性等价约束：

(29)

式中：x为n维决策变量；ζ为随机变量；gi(x,ξ)为随机约束函数；η为给定随机约束条件的置信区间;φ为随机变量的分布函数；K为满足概率理论前提下满足要求的某一数值；sup为上确界。根据式(29)可将约束条件式(15)与式(18)转化为如下确定性表达式：

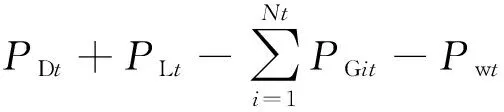
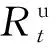
(30)

3 模型求解

3.1 布谷鸟算法

本文构建的模型属于高维、非线性、多约束的优化问题，传统算法很难求解，故采用一种新型智能算法——布谷鸟算法进行求解。该算法受布谷鸟寄生育雏启发被提出，已经成功应用到很多实际问题的优化中。其搜索过程基于布谷鸟产卵过程的3种理想假设：

1) 每只布谷鸟一次只能产一个鸟蛋，并且随机选择一个鸟巢来孵化它。

2) 在寻窝时最好的鸟巢将会被保留到下一代。

3) 鸟巢的数目固定，假设布谷鸟的卵被鸟窝主人发现的概率是一固定值P(P∈[0,1]).当这种情况发生时，则抛弃重新建窝。

基于以上3条基本假设进行模拟，再根据Lévy-flights随机游走的搜索机制，布谷鸟的寻窝路径和位置更新公式如下：

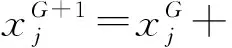
3.2 约束条件的处理

在目标函数中引入惩罚项，将约束问题转化为非约束问题进行求解，流程图如图1所示。经转换

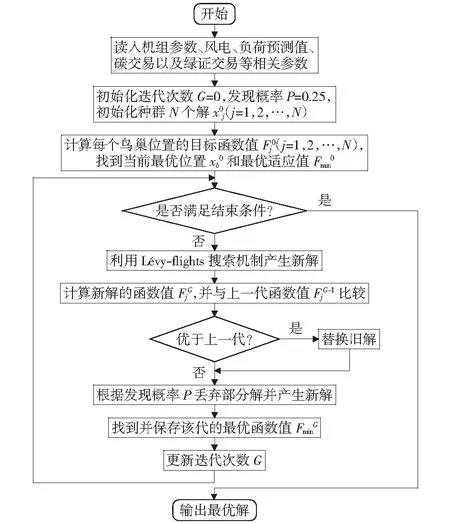
图1 基于布谷鸟算法模型求解流程图Fig.1 Flow chart based on Cuckoo lgorithm

后的目标函数为：

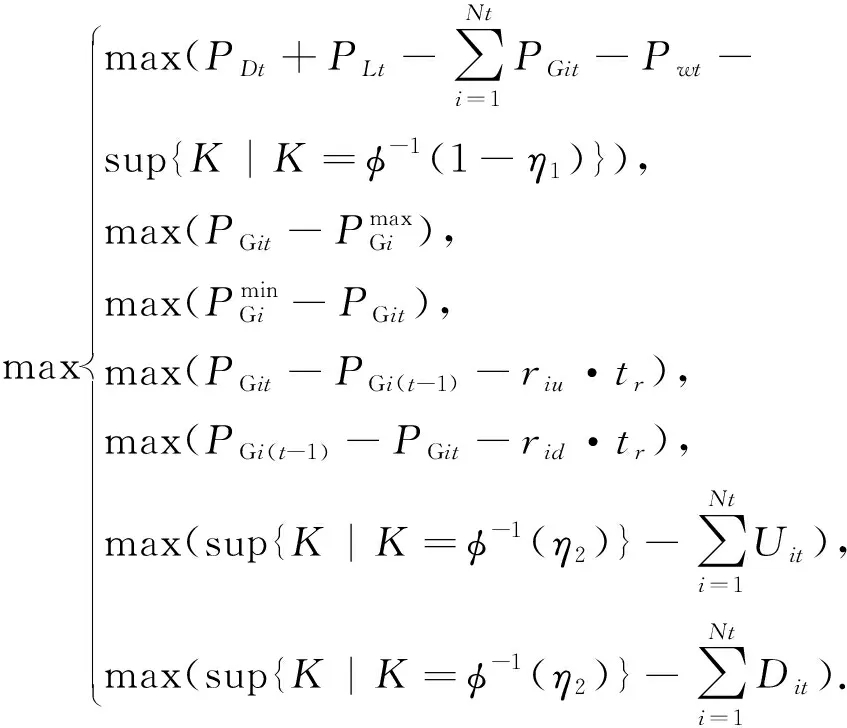
式中：σ为罚因子，大括号里面分别为功率平衡约束、火电机组出力的上下限约束，机组爬坡的上下限约束、单台机组备用约束以及总的备用约束。

4 算例分析

4.1 算例参数

以由10台火电机组与10座风电场组成的某区域电网为例，以1天24 h为决策周期。火电机组参数见文献[19]。切入，额定，切出风速为4，14，25 m/s.装机容量为40 MW.负荷预测误差服从N(0,0.1)正态分布。取可再生能源发电量占总上网电量的配额比例为15%，惩罚裕度为0.02，惩罚价格为100元，系统基准线排放因子取0.798，碳抵消额为碳分配额2%，碳抵消额买卖价格为22元，碳分配额买卖价格为55元，η1，η2和η3取0.95.24 h时间段的风速及负荷预测情况如图2所示。

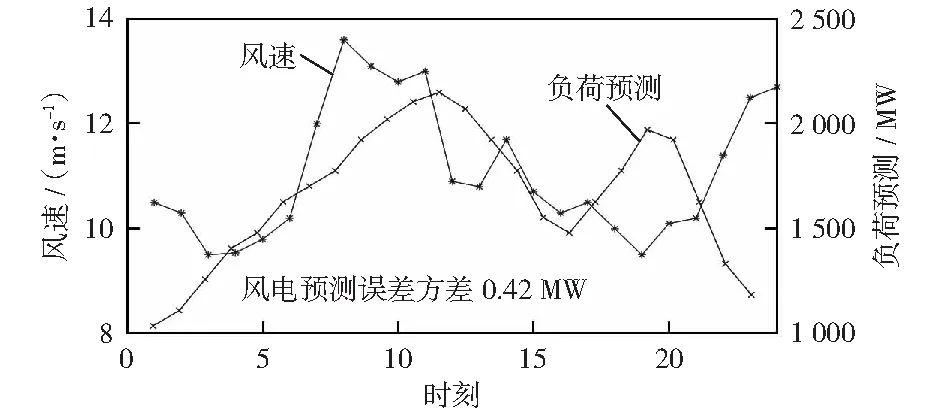
图2 24 h时段内风速与负荷预测值Fig.2 Wind speed and load forecast value in 24 h period

4.2 Z'参数的选取

可再生能源发电量直接影响TGC成本。本文利用算例参数计算单独考虑TGC机制的机组出力值，并与传统调度机组出力值进行比较；Z'的取值由测量时段内出力最大变化机组决定。机组出力如图3、图4所示。

机组单位电量CO2排放强度Zi依次为0.97，0.97，0.98，1.23，1.21，1.18，0.86，1.08，1.80，0.73 kg/MWh.

图3 考虑TGC机制经济调度与传统经济调度机组出力Fig.3 Unit output of the economic dispatch considering TGC mechanism and traditional economic dispatch

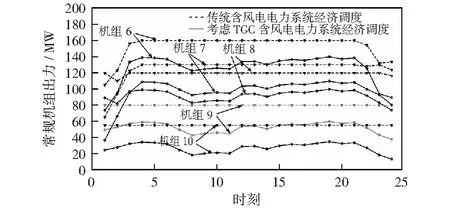
图4 考虑TGC机制经济调度与传统经济调度机组出力Fig.4 Unit output of the economic dispatch considering TGC mechanism and traditional economic dispatch

由图3、图4可知，引入TGC机制后，24个时刻的10台机组出力都发生了变化。通过计算机组各时刻的出力变化程度，确定每个时刻Z'的取值，如表1.

表1不同时刻Z'的取值

Table 1 Values ofZ' at different moment

kg/MWh

4.3 算例结果分析

4.3.1 机组出力结果分析

为了研究引入绿证-碳交易机制对电力系统调度的影响，对比分析考虑TCC机制的含风电电力系统调度与传统含风电电力系统调度机组出力，结果如图5、图6所示。其中虚线代表传统含风电电力

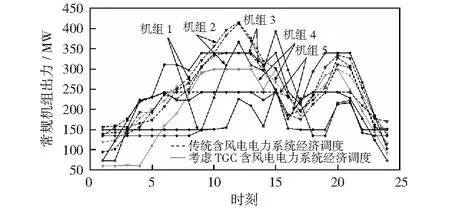
图5 考虑TCC机制经济调度与传统经济调度前5个机组出力Fig.5 First five units output of the economic dispatch considering TCC mechanism and traditional economic dispatch

系统调度机组出力，实线代表考虑TCC的含风电电力系统调度机组出力。比较传统调度模型下机组出力与考虑TCC机制调度模型下机组出力的差值。

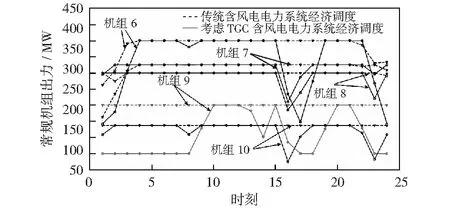
图6 考虑TCC机制经济调度与传统经济调度后5个机组出力Fig.6 Last five units output of the economic dispatch considering TCC mechanism and traditional economic dispatch

由图5、图6可以看出，引入TCC机制后，10台机组出力均发生变化，前5台机组出力变化波动影响显著，后5台机组出力变化较为平稳，正负变化最为强烈的机组在前5台易波动机组中，其中机组1与机组2正变化最明显，机组1在11时刻出力变化峰值为229.041 4 MW，机组2在9时刻出力变化峰值为145.180 5 MW，机组3为10机组中负变化最为剧烈的机组，负变化率为79.17%，出力变化峰值为-91.201 5 MW；其余机组只会在某个单独时刻出现负变化；前5台机组在0～12时刻出力呈上升趋势，且在12时刻达到峰值，10机组在12～24时刻虽有短暂出力上升时刻，但仍以下降趋势为主，原因在于在0～12时刻风电出力值与负荷值是处于不断上升趋势，虽引入TCC机制后降低了大部分机组出力，但整体机组出力变化趋势仍是受风电出力与负荷需求所控制呈上升趋势，在12～24时刻风电出力与负荷需求整体呈下降趋势，风电虽在部分时刻出力增加，但大部分时刻不如负荷需求下降程度与幅度，故火电机组出力整体呈下降趋势，但在部分时刻有上升趋势；10机组在24个时刻以正变化为主，正变化率为86.25%，表明引入TCC机制后，机组出力以减少为主，火电机组发电成本随之降低。

4.3.2 绿证-碳交易结合影响分析

TGC成本与CT成本通过单位供电CO2强度Z'实现模型一体连接，且风电出力值影响着TGC成本，图7给出了24时刻风电预测值、TGC成本与CT成本的曲线。

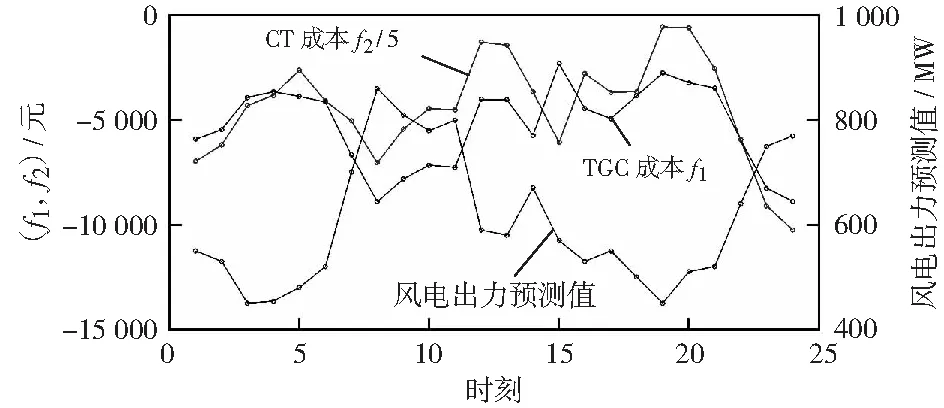
图7 24 h时段风电预测值、TGC成本与CT成本Fig.7 Forecast value of wind power, TGC cost and CT cost in 24 h period

由图7可知，不同的风电预测值对应不同的TGC与CT成本；在大部分情况下，风电预测值与两种成本负相关，TGC成本与CT成本正相关，在风电出力降低的时段内，TGC成本与CT成本会有不同程度的增加，在TGC成本增加的时段，CT成本由不同程度的增加。风电出力通过影响TGC成本进而影响CT成本。

在4～5时刻，风电上升，此时TGC成本却呈现负相关联系。采用皮氏积矩相关系数(pearson product-moment correlation coefficient，PPCC)计算TGC成本与CT成本影响关系，计算公式如下：

式中：r(f1,f2)为PPCC；Cov(f1,f2)为f1与f2的协方差；Var[f1]为f1的方差；Var[f2]为f2的方差；将f1与f2数值以矩阵形式带入求解，得出r的取值为0.733 6，即CT成本受TGC成本影响程度为73.36%.同理计算出f1与P2影响程度为-89.50%，f2与Pw影响程度为-56.82%，可见TGC成本受风电预测出力波动较大。

4.3.3 CT模型灵敏度分析

本算例中风电渗透率为30%～40%之间，属于含高比例可再生能源电力系统；风电的高比例引入使得TGC函数大部分数值落在三段函数盈利范围内，惩罚裕度的变化对TGC成本影响较小，在此不做考虑；CT模型的灵敏度分析主要考虑碳抵消额裕度变化对CT成本、TGC成本、火电机组运行成本及整体成本的影响；碳抵消额与碳分配额买卖价格由具体交易市场决定，故本文不对其进行具体考虑。采用控制变量进行计算，即在算例参数中，改变碳抵消裕度的值，具体数据见表2.

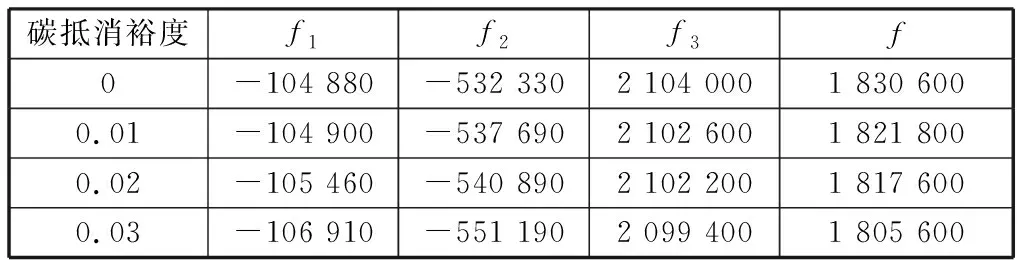
表2 不同碳抵消额裕度下的CT成本、TGC成本、火电机组成本与总成本Table 2 CT cost、TGC cost、thermal power unit cost and total cost under different carbon offset margin 元

由表2可以看出，在引入CT机制后，CT成本、TGC成本、火电机组运行成本与总成本不同程度上减少，且随着碳抵消裕度的增大而递减。在裕度为3%时，CT成本与裕度为0时相比下降1.94%，TGC成本下降3.54%，火电机组运行成本下降2.186%,总成本下降1.365%，虽有成本减少情况，但减少幅度较小。碳抵消机制是对传统碳交易模型的补充，其裕度不超过规定碳分配额的5%，裕度的基数偏小，最后对结果的影响程度随之偏小。碳抵消裕度的增加使整体规定排放量增加，碳交易大多数处于出售多余碳分配额和碳抵消额盈利的状态；由于整体规定的排放量增加，电厂将花费更少的成本来向碳交易市场购买不足碳量导致其成本的下降；CT成本与TGC成本是正相关关系，CT成本的减少会影响TGC成本不同程度地减少。

4.3.4 消纳能力分析

在大规模风电并网情况下，本文从系统弃风成本与备用成本角度来考虑风电消纳能力，结果见表3.

表3 TCC调度和传统调度的系统运行成本Table 3 Cost of system ooperation of TCC dispatch and the traditional dispatch 元

由表3可以看出，在调度模型中引入TCC，弃风成本较传统调度下降13.29%，火电机组运行成本下降了18.33%，备用成本增加13.63%，总成本下降37.98%.算例中风电出力占整体比重为30%～40%，TGC成本与CT落在盈利区间比重较大，故TCC成本为负值处于盈利状态；TCC机制引入后，86.25%的机组出力值为正变化，机组出力减少，火电成本减少；TCC机制以CT与TGC两种具体机制对风电进行量化买卖处理，并设置惩罚机制，市场买卖机制在新能源政策中可促进新能源的开发利用，弃风成本响应减少；高比例风电的引入对系统的安全性构成威胁，系统用来应对高比例风电的出力随机性与波动性的旋转备用成本相应提高。备用成本增加外，弃风成本与总成本均下降较大比重。TCC机制的应用提高了风电消纳能力，降低了总体经济成本，同时也增加了应对大规模风电并网波动特性的备用成本。

5 结论

为探求新电改能源政策对调度的影响，本文提出了基于TCC的含风电电力系统优化调度模型，并验证了所提模型的有效性，主要结论如下：

1) TCC机制的引入能大范围降低常规火电机组出力，减少火电机组发电成本。

2) TGC成本与CT成本通过单位供电CO2排放强度结合，受风电出力影响，且TGC成本受风电影响较大。

3) 碳抵消机制的引入降低了CT成本、TGC成本、火电机组运行成本与总成本，但降低幅度偏小。

4) TCC机制的引入提高了风电消纳能力，降低了总体经济成本，却增加了一定比重的备用成本。