基于主成分分析的图像分割方法

孙前来，王 银，孙志毅，杨 凯，刘瑞珍

(太原科技大学 电子信息工程学院，太原 030024)

图像分割是机器视觉中图像处理的一个重要和关键的过程，是图像识别和图像理解的基础。阈值分割是最早的图像分割方法之一，适用于目标和背景有着不同灰度值范围的图像。阈值分割具有方法简单、计算量小、性能稳定等众多优点，因而成为最基本和应用最广泛的图像分割技术。图像的阈值分割主要是根据图像的灰度特征，选取一个或多个阈值，将图像中所有像素的灰度值与阈值相比较，把整个图像的像素分为两类或者以上，从而将图像划分成背景区域和一个或者多个目标区域。

在图像分割之前，难以确定图像中目标区域像素所属的不同灰度值范围的数量，导致难以事先确定图像分割所需阈值的数目，这是阈值分割方法的难点之一。此外，阈值的选取适当与否会直接影响图像分割的精度和图像描述分析的正确性，所以阈值分割方法的另一个难点是如何找到合适的阈值将背景像素和目标像素分开。当图像中含有多个分别属于不同灰度值范围的待分割目标时，需要多个阈值才能取得较好的分割效果，然而找到多个“最优”阈值的组合更加困难，需对其进行优化。早期的阈值优化方法多基于穷举搜索，如最大类间差法(OTSU).但是对于图像的多阈值分割，利用穷举搜索的方法寻找“最优”阈值组合所消耗的时间会随着期望阈值数量的增加呈指数规律增长。为了提高图像分割的质量或减少图像分割的时间消耗，目前大多数多阈值分割方法采用各种优化算法对阈值数量和阈值大小同时进行优化以确定图像分割 “最优”阈值组合，如遗传算法[1-3]、粒子群算法[4-6]、人工蜂群算法[7-9]及其他优化方法[10-13]。采用优化算法确定“最优”阈值组合，不仅增加了多阈值分割方法的复杂性，而且对阈值进行优化时存在陷入局部最优问题的可能。

如果能够找到一种方法，可以事先确定待分割图像中背景或目标像素的灰度特征，从而避免同时对阈值数量和大小进行优化所带来的问题，还可以降低图像分割的难度。本文针对背景相对简单的一类图像，提出了一种基于主成分分析(principal component nalysis,PCA)的缺陷分割方法。该方法利用PCA对图像进行线性变换，将原始图像中背景像素的灰度值变换到重建图像中的零附近，从而将待分割目标分为两类，相当于事先就确定了图像中背景像素的灰度特征，使得图像分割较为容易。由于原始图像中背景像素的灰度值被转换为接近于零，即使图像中存在多个具有不同灰度值范围的待分割区域，仅使用两个阈值就能将目标与背景区分开。

1 主成分分析

PCA就是通过正交变换将一组可能存在相关性的变量转换为一组线性无关的变量，目的是去除原始数据中向量之间的相关性，突出原始数据中的隐含特征。PCA通常用来减小图像的尺寸或去除噪声，是统计方法中最成功的图像识别和压缩技术之一[14]。PCA还广泛应用于图像的去噪、特征提取及融合等领域。实现主成分分析有两种基本方法，一种是特征值分解，一种是奇异值分解。可以证明，奇异值分解和特征值分解是等价的[15]。

本文选择使用奇异值分解来实现主成分分析。首先简要地给出奇异值分解定理。

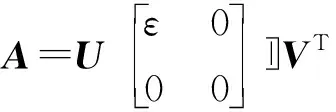
(1)

式中：ε=diag(σ1,σ2,…,σr)；酉矩阵U和V分别为矩阵A的左奇异矩阵和右奇异矩阵。列向量ui(i=1,2,…,m)和vj(j=1,2,…,n)分别称为矩阵A的奇异值σi的左奇异向量和右奇异向量。

(2)

式中：ui和vi分别为矩阵A的前r个左右奇异向量。

根据这一结论，有理由认为相较于较大的奇异值，接近于零的奇异值对应的主成分只含有少量矩阵重构所需信息，在对矩阵近似重构时也可以忽略。所以，矩阵A可以由下式近似重构：

(3)

2 基于PCA的图像分割方法

针对多阈值图像分割方法中寻找“最优”阈值组合所存在的算法复杂和时间开销较大等问题，本文提出了基于主成分分析的图像分割方法，可以对背景相对简单的图像进行分割。

2.1 方法的提出

假设在理想情况下，图像背景单一且均匀，待分割目标总面积占图像面积比例较小，而且不考虑噪声和不均匀光照等的干扰。此时，图像的背景就成为了图像的主要信息，而待分割目标是图像的次要信息。由PCA可知，奇异值越大的主成分含有原始数据的信息也就越多；如果利用除第一主成分之外的其它主成分对图像进行重建，那么重建图像中将主要包含待分割目标的信息，有利于图像的分割。为了减少图像分割时的计算量，利用奇异值累计贡献率达85%时的前若干主成分对图像进行重建，即

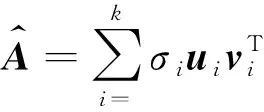
(4)

式中，k为奇异值累计贡献率达到85%时奇异值的数量。

图1(a)为理想情况下的8位灰度图像，图中黑点和白点分别用来模拟属于不同灰度值范围的待分割目标。对图1(a)进行奇异值分解并按照式(4)对图像重建，利用两个阈值对重建图像进行分割，结果如图1(b)所示。图1(c)为理想图像的灰度统计直方图，由图可知其背景像素的灰度值为128.重建图像的直方图如图1(d)所示。

图1 理想图像的分割结果Fig.1 Segmentation of an ideal image

经过线性变换后，原始图像中背景像素的灰度值被变换到重建图像中零附近。在重建图像中，“灰度值”可能会出现小于零的情况，这和原始图像中灰度值小于背景的像素对应；大于零的部分和灰度值大于背景的像素对应。此时，目标被分成两类，一类比背景暗，一类比背景亮，可以利用两个位于零附近的阈值在重建图像中对目标进行分割。

图1说明基于PCA的缺陷分割方法在理想情况下是有效的，接下来以实际情况下的图像对其有效性进行验证。图2(a)为一张实际图像，图2(b)为分割结果，图2(c)和(d)分别为图像重建前后的直方图。由图2可知，经图像重建后，原始图像中背景像素的灰度值同样被转换到重建图像中零附近。

图2 实际的分割结果Fig.2 Segmentation of a real image

2.2 图像分割的具体步骤

基于主成分分析的图像分割方法的具体步骤如下：

1) 首先对待分割图像进行灰度化得到灰度矩阵M，对灰度矩阵M进行奇异值分解，得到M的左/右奇异矩阵U和V；

2) 计算奇异值的累计贡献率，累计贡献率达到85%时停止计算并记下当前奇异值的个数k；

4) 找到合适的阈值T1和T2，且满足T1>0和T2<0；

5) 利用阈值对图像进行分割，得到二值化的分割结果。

3 图像分割实验

为了验证基于主成分分析的图像分割方法的有效性，在MATLAB软件环境下对图3(a)所示的实际图像进行分割实验，结果如图3(b)所示。同时利用MATLAB自带的经典阈值分割方法OTSU和基于Canny算子的边缘检测方法工具箱对图像进行分割，结果分别如图3(c)和(d)所示。图3(a)中除第二张和最后一张之外，其余图像均来自于以色列威兹曼科学院的图像分割数据集。

由图3中大米图像的分割结果可知，当待分割目标在整个图像中占比较大时，本文方法仍能取得较好的分割结果。如图3中第二、三图像的分割结果所示，当图像中背景和目标像素值较为接近时，基于Canny算子的边缘检测算法的分割效果优于本文方法和OTSU法，但该方法对纹理较为敏感。OTSU方法只能分割出相对于背景而言或明或暗的一类目标。

为了进一步验证本文方法在不均匀光照和噪声等干扰情况下的有效性，以采集于不同的实际生产环境、带有典型缺陷的带钢图像为例，对其表面缺陷进行分割实验， 并与OTSU法和基于Canny算子的边缘检测方法进行对比，结果如图4所示。图4(a)中，从左到右依次为带有多个孔洞、擦痕、辊印、黑斑、锈痕以及单个孔洞等缺陷的带钢图像。

由带钢表面缺陷的分割结果可知，OTSU法对不均匀的光照较为敏感，导致其存在对缺陷不能有效分割的情况。基于Canny算子的边缘检测方法对噪声和纹理极为敏感，分割结果将给后续的缺陷识别和分类带来较大困难。

以上实验结果验证了基于PCA的图像分割方法的有效性。图像分割实验结果表明，该方法对噪声和不均匀的光照均不敏感，分割效果总体上优于OTSU法和基于Canny算子的边缘检测方法。

图3 多张实际图像的分割结果Fig.3 Segmentation of some real images

图4 带钢典型缺陷的分割Fig.4 Segmentation of steel strips with typical defects

4 结论

对于背景较为简单的一类图像，基于主成分分析的图像分割方法可以通过线性变换将图像中背景像素的灰度值变换到零附近，从而仅利用两个零附近的阈值就能够对图像中处于不同灰度值范围的目标进行分割。采集于不同环境下的图像的分割实验验证了该方法的有效性。该方法可以事先确定图像分割所需阈值数量，而且只有两个阈值的大小需要优化，降低了多阈值分割方法中阈值优化算法的复杂性和阈值优化所需的时间开销。

基于主成分分析的图像分割方法的局限性在于只适用于背景相对简单且待分割目标面积在整个图像中占比相对较小的场合。因此，该方法需要进一步改进以扩大其适用范围并降低其时间复杂度。