面内载荷作用下功能梯度板动力屈曲

王 鑫，龙梦璇，韩志军，吴亚丽

(太原理工大学 a.力学学院，b.建筑与土木工程学院，太原 030024)

功能梯度材料是由两种或多种材料构成的新型复合材料，具有不同材料之间呈现光滑连续的特性，可以有效避免传统复合材料因材料属性微观不均匀而引起的应力集中以及分层、开裂等现象。功能梯度材料由于优越的力学性能而备受学术界关注[1-2]，在航空航天、机械工程、生物医学工程以及核工程等诸多领域得到了广泛应用，科研人员对功能梯度板的动力屈曲的探究也不断深入[3-4]。FELDMAN et al[5]研究了功能梯度板在面内载荷作用下的弹性动力屈曲，并给出了增强项的最佳空间分布。LATIFI et al[6]基于经典板理论，采用傅里叶级数展开研究了各种边界条件下面内载荷矩形功能梯度板的动力屈曲。BODAGHI et al[7]采用细观力学模型，给出了简支条件下非均匀分布面内动力载荷矩形功能梯度板屈曲解析表达式。NG et al[8]基于经典板理论，讨论了功能梯度圆柱壳和矩形板在面内周期载荷作用下的动态屈曲。KOWALMICHALSKA et al[9]采用经典板理论通过有限元法获得了含有裂纹的功能梯度板临界屈曲载荷。RAD et al[10]基于经典板理论，通过有限元法研究了含初始缺陷的功能梯度板的屈曲问题。KHORSHIDI et al[11]基于经典板理论，研究了考虑指数剪切变形下功能梯度纳米板的屈曲。 MANTARI et al[12]基于经典板理论和双曲线优化方程，对功能梯度夹层板在面内载荷作用下的动力屈曲、振动以及弯曲进行了分析。

综上所述,目前对功能梯度板屈曲问题的研究大多采用数值解法和计算机仿真。基于此，本文使用Kirchhoff薄板理论与Vogit应变假设，用Hamilton原理得到各项物性参数服从幂律分布的功能梯度板的动力屈曲控制方程；用分离变量法及试函数法，得出功能梯度板满足边界条件的动力屈曲临界载荷解析表达式，与用棣莫弗公式结合李兹法得到的动力屈曲临界载荷相同。运用MATLAB软件编程对临界载荷解析表达式进行数值计算，讨论了功能梯度板的几何尺寸、梯度指数、模态阶数以及构成材料的各项物性参数对临界载荷的影响。

1 功能梯度材料的物性参数

基于Vogit等应变假设及线性混合率，假定功能梯度板各项物性参数仅沿厚度方向变化，陶瓷材料体积率遵循幂律分布[13-14]：

(1)

则板内任意一点的物性参数可表示为:

(2)

2 控制方程推导

功能梯度板在x=0处为夹支边界条件，在x=Lcr处为固支边界条件，在y=0和y=Lb处为简支边界条件，此类板简称CFSS板，如图1所示。

图1 CFSS功能梯度板加载示意图Fig.1 CFSS functionally graded material plate under the in-plane load

根据Kirchhoff薄板理论及经典弹性理论，位移与应变关系为：

(3)

功能梯度材料的本构关系为：

(4)

功能梯度板的内力及内力矩为：

(5)

功能梯度板的刚度矩阵的系数表达式为：

(6)

功能梯度板具有横观各项同性的力学性能[15]，可知：

A16=A26=B16=B26=D16=D26=0 .

(7)

功能梯度板发生屈曲时的变形能为：

(8)

动能(考虑转动惯量)为：

(9)

式(9)中定义广义惯量为:

(10)

外力功为：

(11)

(12)

(13)

(14)

将式(5)代入式(12)-式(14)可得：

根据Kirchhoff薄板理论，薄板中面在变形过程中没有伸长变形，所以含u0,v0的项可以忽略[16]，得出功能梯度材料在面内载荷作用下的动力屈曲控制方程：

D11wxxxx+(2D22+4D66)wxxyy+D11wyyyy+N(t)wxx-I0w+I2wxx+I2wyy=0 .

(16)

3 控制方程的求解

设薄板平面的法向位移为[17]：

(17)

代入控制方程化简可得：

(18)

对式(18)分离变量可得：

(19)

式中：

当λ<0时，其解为指数型发散解，系统呈现不稳定状态。当λ>0时，系统围绕平衡位置做微小扰动[18]。所以当λ<0,(α-λξ)2-4(β-λξ)>0时，平板发生屈曲，其动力屈曲解为：

X(x)=C1sink1x+C2cosk1x+
C3sink2x+C4cosk2x.

(20)

式中：

式(20)满足下列一端夹支、一端固定、另外两端简支功能梯度材料板的边界条件：

(21)

将式(20)代入式(21)中得：

(22)

若该方程有非奇异解，其系数行列式必为0.可得：

(23)

分析该式可得：

(24)

由式(24)可得一端夹支、一端固定另外两端简支板临界屈曲载荷为：

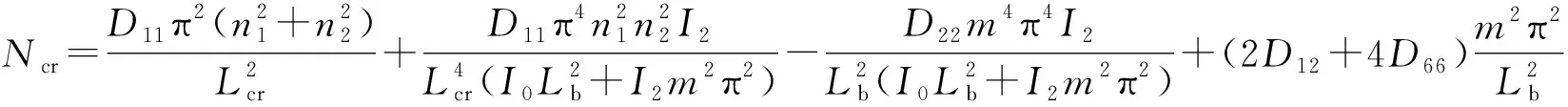
(25)

式中：n1=1,2,3,…;n2=n1+2;m=1,2,3,….由式(17)、式(20)、式(21)联立求解，得屈曲解表达式：

(26)

用里兹法和棣莫弗公式结合计算CFSS板动力屈曲[15]，根据边界条件可取：

(27)

式中：n1=1,2,3,…;n2=n1+2;m=1,2,3,… .将式(27)代入控制方程式(16)，经化简运算，得到临界载荷表达式为：

(28)

该方法所得结果与本文中式(25)不考虑转动惯性的动力屈曲临界载荷结果相同。

将功能梯度板梯度指数k值取为0，根据幂律分布及物性参数表达式(1)、式(2)，功能梯度材料蜕化为单质金属材料。临界屈曲载荷表达式化简为：

(29)

4 数值计算

本文应用MATLAB软件编程对式(25)计算分析，以CFSS功能梯度矩形板为例，加载方式与几何尺寸见图1，具体材料参数取值见表1.

表1 材料各项物性参数Table 1 Physical parameters of component materials

图2是当CFSS功能梯度板的宽度Lb、厚度h、梯度指数k、X方向模态数m、Y方向模态数n相同，构成材料不同时，动力屈曲临界载荷Ncr与临界长度Lcr的关系曲线。

图2 构成材料不同时临界载荷与临界长度的关系Fig.2 Relationship between the critical load and length when material is different

图2表明，Ncr随Lcr的增加呈指数式下降。当Lcr相同时，(陶瓷-铁)板的临界载荷高于(陶瓷-钛)板，而(陶瓷-钛)板与(陶瓷-铜)板的临界载荷曲线几乎重合。参照表1，材料钛和铁的弹性模量差距较大，材料钛和铜泊松比差距较大。结合图2和表1数据分析可得：材料的弹性模量变化对功能梯度板动力屈曲临界载荷的影响较为明显，泊松比影响相对较小。

图3是当CFSS功能梯度板的h、k、m、n与构成材料相同，Lb不同时，Ncr与Lcr的关系曲线。

图3 宽度Lb不同时临界载荷与临界长度的关系Fig.3 Relationship between the critical load and length when width is different

由图3可知，当Lcr相同时，Ncr随Lb的增大而减小。当功能梯度材料板的长宽比小于1/2时，Ncr随Lcr变化明显；大于1/2时，Ncr随Lcr的变化趋于平缓。

图4是当CFSS功能梯度板的Lb、h、m、n与构成材料相同，k不同时，Ncr与Lcr的关系曲线。当Lcr相同时，Ncr随k的增大而减小。k越小，Ncr随Lcr的变化越明显，k值在(0，1)的范围内变化对Ncr的影响较大。不同k值对应的临界载荷曲线随Lcr的增加逐渐趋于水平。

图4 梯度指数k不同时临界载荷与临界长度的关系Fig.4 Relationship between the critical load and length when gradient index is different

图5是当CFSS功能梯度板的Lb、h、k、m与构成材料相同，n不同时，Ncr与Lcr的关系曲线。当Lcr相同时，Ncr随n的增大而增大，n值越高，Ncr随Lcr变化越明显，表明临界载荷越大，功能梯度板的高阶屈曲模态越容易被激发。当临界长度达到一定值时，不同的X向模态数对应的临界载荷逐渐趋于一定值。

图5 X方向模态数n不同时临界载荷与临界长度的关系Fig.5 Relationship between critical load and length when the modal number of X direction is different

图6是当CFSS功能梯度板的Lb、h、k、n与构成材料相同，m不同时，Ncr与Lcr的关系曲线。当Lcr

图6 Y方向模态数不同时临界载荷与临界长度的关系Fig.6 Relationship between critical load and length when the modal number of Y direction is different

相同时，Ncr随m的增大而增大，且m越大，相邻模态数对应的Ncr差值越大，不同m值对应的曲线随Lcr的增大逐渐趋于水平。这也表明：临界载荷越大，越容易激发高阶模态。

图7 构成材料不同时临界载荷与厚度的关系Fig.7 Relationship between critical load and thickness when material is different

图7是当CFSS功能梯度板的Lcr、Lb、k、m、n相同，构成材料不同时，Ncr与h的关系曲线。由图可知，图7表明，Ncr随h的增大而增大。当h相同时，陶瓷-铁板的临界载荷高于陶瓷-钛板，而陶瓷-钛板与陶瓷-铜板的临界载荷曲线几乎重合，表明材料的弹性模量变化对屈曲临界载荷的影响较为明显，泊松比的影响相对较小，与图2所得结论相符。

图8是当CFSS功能梯度板的Lb、k、m、n与构成材料相同，Lcr不同时，Ncr和h的关系曲线。当Lcr一定时，Ncr随h的增大而增大。当h相同时，Ncr随Lcr的增大而减小，且Ncr降幅随Lcr的增加呈递减趋势，与图3所得结论相符。

图8 临界长度Lcr不同时临界载荷与厚度的关系Fig.8 Relationship between critical load and thickness when length is different

图9是当CFSS功能梯度板的Lcr、Lb、m、n与构成材料相同，k不同时，Ncr与h的关系曲线。当h相同时，Ncr随k的增大而减小，k值越小曲线倾斜度越大，k值在(0，1)的范围内变化对临界载荷的影响明显，与图4所得结论相符。

图9 梯度指数k不同时临界载荷与厚度的关系Fig.9 Relationship between critical load and thickness when gradient index is different

图10是当CFSS功能梯度板的Lcr、Lb、k、m与构成材料相同，n不同时，Ncr和h的关系曲线。当h相同时，Ncr随n的增大而增大；n越大，曲线倾斜度越大，相邻模态数对应的Ncr差值越大。这表明：高阶模态对临界载荷的影响较明显，低阶模态影响较小。

图10 X方向模态数n不同时临界载荷与厚度的关系Fig.10 Relationship between critical load and thickness when the modal number of X direction is different

图11是当CFSS功能梯度板的Lcr、Lb、k、n与构成材料相同，m不同时，Ncr与h的关系曲线。当h相同时，Ncr随m的增大而增大；并且m越大，相邻阶数对应的Ncr差值越大。结合图10可知, 当功能梯度板厚度变化时，Y方向模态数比X方向模态数对临界载荷影响明显。

图11 Y向模态数m不同时临界载荷与厚度的关系Fig.11 Relationship between critical load and thickness when the modal number of Y direction is different

图12是当CFSS功能梯度板的几何尺寸一定时，两种构成材料的泊松比与动力屈曲临界载荷的关系图。

图12 CFSS板中B、D两种材料之间的临界载荷与泊松比μ1，μ2的关系Fig.12 Relationship between critical load and Poisson ratio when CFSS plate is made up of two materials

由图可知，当功能梯度板的几何尺寸一定时，临界载荷随构成材料的泊松比增大而增大，并且其函数曲线的斜率随泊松比的增大而增大。

图13是当CFSS功能梯度板的几何尺寸一定时，两种构成材料的弹性模量与板动力屈曲临界载荷的关系图。当功能梯度板的几何尺寸一定时，临界载荷随构成材料弹性模量的增大而增大，且变化趋势接近线性关系。

图13 CFSS板中B、D两种材料之间临界载荷与两种材料弹性模量E1，E2的关系Fig.13 Relationship between critical load and elastic modulus when CFSS plate is made up of two materials

图14是当功能梯度板X方向与Y方向模态数取值不同时，功能梯度材料板的屈曲模态图。

由图可知，功能梯度板屈曲模态幅值w，随X方向正向递增，且固定端屈曲模态幅值较大；随Y方向正向不变，且屈曲模态呈正对称或反对称分布。这表明边界条件对功能梯度板的屈曲模态影响较大，模态阶数越大，双向屈曲模态越复杂。

图14 模态数取值不同时的CFSS功能梯度板屈曲模态图Fig.14 CFSS buckling mode image of functionally graded material plate when model number are different

5 结论

1) 基于Vogit应变假设与Kirchhoff薄板理论以及线性混合率，由Hamilton原理导出了功能梯度材料板动力屈曲控制方程式(16).

2) 用试函数法与分离变量法求解，得到了功能梯度材料板在相应边界条件下的动力屈曲临界载荷的解析表达式(25)和屈曲的模态表达式(26)，其屈曲模态如图14.

3) 用MATLAB软件编程计算式(25)和式(26)，讨论了功能梯度板的临界长度、宽度、厚度、梯度指数、材料属性以及屈曲模态阶数对屈曲临界载荷及屈曲模态的影响。结果表明：功能梯度板动力屈曲临界载荷随长度的增大呈指数式下降，随厚度的增大而增大；屈曲临界载荷随梯度指数k的增大而减小，且在(0，1)范围内变化对临界载荷影响较大；屈曲临界载荷随构成材料的弹性模量、泊松比的增大而增大，且弹性模量影响较大，泊松比影响较小；屈曲临界载荷随模态数的增大而增大，当功能梯度板沿Y方向模态数一定时，X方向模态数越大，相邻阶数的临界载荷差值越大，且不同Y方向模态数的临界载荷随长度的增大逐渐趋于水平。当X方向模态数一定时，与上述结论相同；屈曲模态阶数越大，双向屈曲模态越复杂，且屈曲模态变形幅值沿X方向正向递增，固定端变形较大，表明边界条件对功能梯度板的屈曲模态影响较大。面内载荷越大，越容易激发功能梯度板产生高阶屈曲模态。