一类非局部非自治分数阶时滞微分系统的稳定性

郝瑞雪，魏毅强

(太原理工大学 数学学院，太原 030024)

ZHANG et al[1]在2007年研究了下列非线性非自治Riemann-Liouville型分数阶时滞系统(1)

式中：0<α<1，φ(t)是[-r,0)的连续函数，A0，A1是常数矩阵；r是正常数。该文献主要研究系统(1)解的存在唯一性，并且运用广义Gronwall不等式推论证明该系统具有有限时间稳定性。但该文在有限时间稳定性的概念定义上，以及证明过程中都存在较严重的问题。

MIHAILO et al[2]在2008年纠正了文献[1]的错误，研究了线性自治分数阶时滞微分系统与带有控制变量的非自治系统具有有限时间稳定性。

EL-SAYED et al[3]在2009年将问题推广到变系数的情形，研究了下列线性非自治Riemann-Liouville型分数阶时滞系统(2)：

(2)

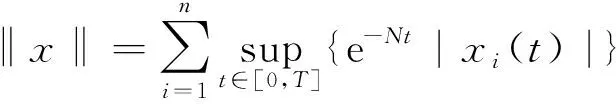
使得解的存在唯一性的证明得以完成。

WANG et al[4]在2015年研究了下列非自治非线性Caputo型分数阶时滞微分系统(3)在非局部初值条件下解的存在唯一性

(3)

式中：0<α<1；A0，A1是常数矩阵。文中有关时滞项的处理方式及Gronwall不等式的灵活应用对同类型问题的研究有可借鉴之处。

本文在前人研究的基础上，将问题推广到下列非局部非自治Riemann-Liouville型分数阶时滞微分系统(4)：

(4)

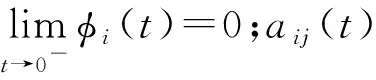
1 预备知识

定义1[5]设函数x∈L[a,b],ρ∈R+,记

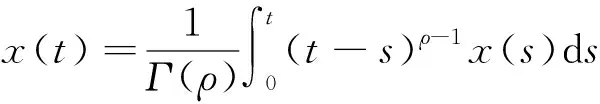
定义2[5]设函数x∈L[a,b],ρ∈R+,m=[ρ]+1,记

称为x(t)的ρ阶Riemann-Liouville型导数。

引理1[5]ρ∈R+,m=[ρ]+1,υ∈C1[0,1],u∈Cm[0,1],Im-ρu∈Am[0,1],则有

1) ∀r,s>0,则IrIsυ(t)=Ir+sυ(t).

2)DρIρυ(t)=υ(t).

u(0).

引理2[6](广义Gronwall不等式)假设g(t)是非负非减的连续函数,0≤t0,a(t),u(t)是[0,T)的非负局部可积函数且

则有

定义3[5]设n>0,记

称为n阶Mittag-Leffler函数。特别地,E1(z)=ez.

定义4[7]齐次方程

满足初始条件x(t)=ψ(t),-τ≤t≤0,关于[δ,ε,t0,J],δ<ε是有限时间稳定的当且仅当

‖ψ‖<δ.

那么

‖x‖<ε.

其中t0是初始时间,J=[t0,t0+T],J⊂R.

把有限时间稳定性的概念推广到非线性系统中，定义如下。

定义5 设∀i,t>0,fi(t,0,0,L,0)=0,称非线性非自治时滞系统(4)是有限时间稳定的,当且仅当‖Φ‖<δ,且‖f‖<α,则有‖x‖<ε.

为了讨论方便,引出几个今后使用的条件：

2 主要结论

定理1 在H1的假设条件下，在C[-r,T]空间内系统(4)与下列系统(5)等价。其中C[-r,T]空间表示[-r,T]上的连续空间。

(5)

证明：当t∈(0,T]时,系统(4)的第一个式子由Riemann-Liouville型导数的定义可得：

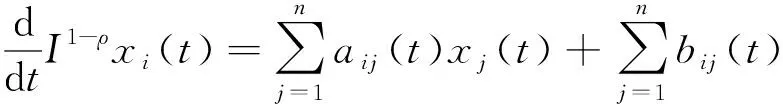
对等号两边同时积分并由系统(4)中的条件I(1-ρ)xi(t)|t=0=0可得：

对等号两边求ρ阶积分得:

对等号两边再求一阶导数即得:

反过来,对系统(5)中的第一个式子等号两边先求(1-ρ)阶积分,再求一阶导数可得：

化解即得:

当t∈(-r,0]时,很显然是恒成立的。

则有

…,xn(t))]|=0.而

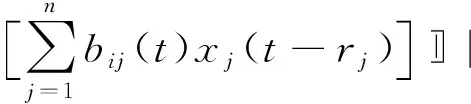
即：

定理2 在H1,H2的假设条件下,如果∃β>1,使得

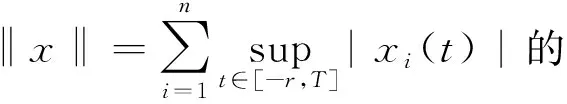
证明：由定理1可知，只要证明系统(5)解的存在唯一性即可。

当t∈[-r,0]时,很显然其解是存在且唯一的。

由于对任意i=1，2，...，10，j=1，2，3，4，y=1，Ey（288））+SD（DEy（288）D（288））＜0.2，因此，群决策矩阵D（288）=（）10×4是全局一致性可接受的决策矩阵，表10所示。

当t∈(0,T]时,定义映射F:C[-r,T]aC[-r,T],则有

先来讨论t∈(r,T].

即：

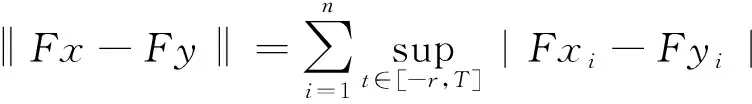
‖bij‖Lβ[0,T]+‖lij‖Lβ[0,T]]‖x-y‖≤

R1‖x-y‖ .

同理,当t∈(0,r]时,有

R1‖x-y‖ .

由于R1<1,所以F是压缩映射,即存在唯一的不动点。因此在C[-r,T]空间内系统(4)存在唯一的解。

定理3 在H1,H2的假设条件下,

取充分大的N,使得

证明：由定理1可知，只要证明系统(T)解的存在唯一性即可。

当t∈(-r,0]时,很显然其解是存在且唯一的。

x

j

(

t

-

r

j

)+

f

i

(

t

,

x

1

(

t

),

x

2

(

t

),…,

x

n

(

t

))] .

为了讨论方便,引出几个今后使用的符号：

先来讨论t∈(r,T].

(s-rj)-yj(s-rj))+(fi(s,x1(s),x2(s),…,

xn(s))-fi(s,y1(s),ys(s),…,yn(s)))]ds|≤

则：

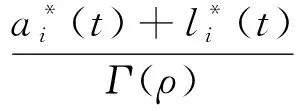
‖x-y‖λ.

即：

R2‖x-y‖λ.

同理, 当t∈(0,r)时,

由于R2<1,所以F是压缩映射,即存在唯一的不动点。因此在C[-r,T]空间内系统(4)存在唯一的解。

定理4 在定理3的假设条件下,若对于∀i,t>0,fi(t,0,0,K,0)=0,‖f‖<α,‖Φ‖<δ,且

成立,则在C[-r,T]空间内范数

的意义下系统(4)具有有限时间稳定性。

证明：设x(t)=(x1(t),x2(t),…,xn(t))是系统(4)的解。

当t∈[r,T]时,

x2(s),…,xn(s))|ds.

从而

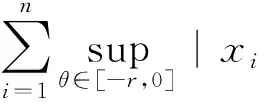
对上式分析可知,满足运用广义Gronwall不等式的条件,因此运用广义Gronwall不等式可得:

从而

{Eρ[(‖A‖+‖B‖)Tρ]-1} .

则

那么

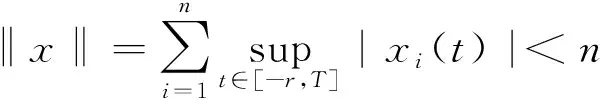
{Eρ[(‖A‖+‖B‖)Tρ]-1}<ε.

当t∈(0,r]时,同理可得，‖x‖<ε.

由此可知,系统(4)具有有限时间稳定性。