在位测量实现转子中心孔加工位置精度的研究
关惠予,张辽远,赵书剑
(沈阳理工大学 机械工程学院,沈阳 110159)
现代航空、航天、兵器等国防工业领域的许多重要零件为薄壁结构,并且具有结构复杂、零件精度要求高的特点[1],在工业、农业等各个领域也得到广泛应用,大到汽车和飞机发动机的零部件、大型轮船上的部件以及工业生产设备的部件,小到惯性元件的框架结构、转子结构等都是薄壁回转体结构,其在国民经济和国防中占有很大的比重[2]。薄壁回转体的制造精度有着严格的要求,能够对薄壁回转体进行精密测量是确保薄壁回转体制造精度的有效手段[3]。转子常以中心孔与轴配合进行定位,孔的位置直接影响转子的安装精度、机器的使用寿命[4]以及能耗等。为保证转子能最大程度的发挥使用性能,精准的确定中心孔的加工位置成为加工过程中尤为重要的一步。本文以在位测量方法研究磁性转子中心孔的加工位置精度。
1 零件分析
1.1 转子的材料分析
工件为磁性转子,体积小、壁薄、机械强度高、尺寸精度高、形状复杂、性能稳定,具有良好韧性,并可嵌入金属件及塑料件等优势。转子的材料是内含聚醚醚酮(PEEK)树脂的新型复合磁性材料,多极充磁。聚醚醚酮具有优良的综合性能,在许多特殊领域可以替代金属、陶瓷等传统材料;其耐高温、自润滑、抗疲劳等特性,使之成为当今最热门的高性能工程塑料之一,主要应用于航空航天、汽车工业、电子电气和医疗器械等领域[5]。
1.2 转子的结构分析
图1为转子注塑毛坯件,轮廓无定位基准,叶片方向尺寸略大;外轮廓使用外径千分尺测量,垂直于轴线截面尺寸,外圆直径误差为0.05mm左右。转子自带φ3孔,但位置精度不能保证。
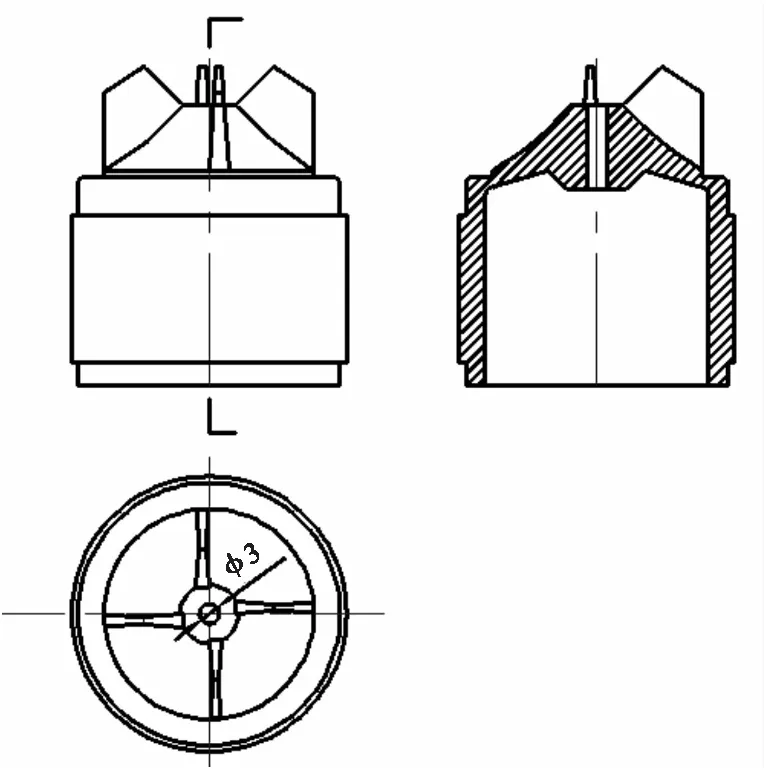
图1 转子的外部轮廓
1.3 转子的加工要求
转子加工要求高,要求将标准轴插入中心孔;以轴中心作为转子的回转中心时,转子外轮廓圆跳动在0.03mm以内,中心孔尺寸在φ3.985~ 3.995mm之间。
2 在位测量
本实验均采用在位测量方法进行中心小孔位置的确定及加工,在不拆卸工件的情况下对工件进行测量。对于回转类零件的测量,用离线法测量时,工件需要在加工设备和测量设备之间来回转移,导致加工时的定位基准与检测时的基准不重合,工件上定位基准的制造误差所造成的定位基准位移[6]等以及返修调整时再次装夹所产生的误差都会影响实验结果。在位测量可免除离线检测由于定位基准所带来的误差[7],因此在位测量结果更接近于实际加工情况。在位测量技术是回转类零件机械加工发展的必然趋势,特别是小批量生产的高精度回转类零件,该类零件的测量技术是关乎其生产质量的重大关键性技术,对检测精度和效率的要求也越来越高[8]。
3 工件的定位方法
该磁性转子壁薄,质软,易碎,受压受热易变形,选用三爪卡盘以外轮廓定位时,在集中力的作用下,转子受力发生形变,距卡爪60°位置变形最大,变形位置向外突出,一旦松开卡爪,转子弹性恢复,使内孔变成三棱形,不利于保证孔位置精度[9]。图2为三爪卡盘定位时,零件夹紧变形示意图。
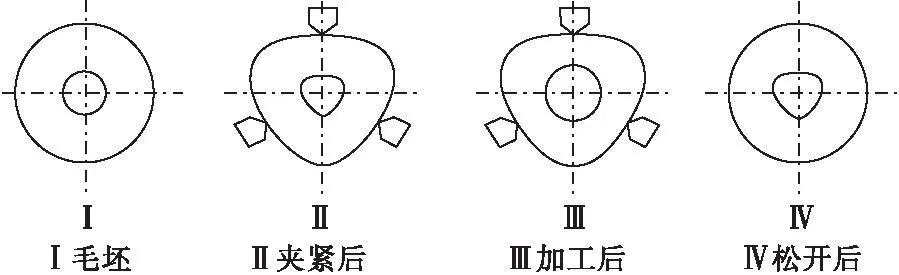
图2 零件夹紧变形
将集中力改为均布力,外圆夹紧仍易变形,因此选择以工件内孔定位工件,均布力分布如图3a所示。定位心轴与转子内孔采用过盈紧配合时,心轴在工件安装与拆卸过程中易划伤工件内壁;心轴尺寸过大导致零件变形,加工后零件回缩,引起中心位置发生变化、孔的形状误差等,降低工件质量。因此定位心轴与转子内孔采用过渡配合。经实际工件测量,内孔尺寸为φ34.32~34.33mm。设计心轴时加工的实际尺寸与毛坯内孔表面不能完全重合,心轴局部尺寸大于内孔尺寸,导致工件与心轴配合时工件倾斜。因此心轴采用阶梯轴,中部尺寸小于工件内孔,工作部分两端起定位作用。
考虑到以上因素影响,心轴材料选用铝,定位部分尺寸为φ34.325mm,顶端有2×45°的倒角,心轴上端面中心加工一个φ5mm的孔,目的是为储存加工时的断屑,防止断屑堆积影响加工效果。图3b为转子、心轴、卡盘安装示意图。安装时心轴与转子固定在卡盘上,便于加工。

图3 工件定位示意图
4 中心孔的加工方法
本实验中心孔加工采用DMU50五轴联动机床。加工方法采用铣和铰;由于材料的受热膨胀,加工刀具选用需大于孔要求尺寸,因此选用φ3.99mm Sandvik两刃的硬质合金圆柱铣刀,转速1200r/min,进给速度为50mm/min;φ4.0mm的直刃硬质合金直柄铰刀,转速400r/min,进给速度为20mm/min。图4为实际加工示意图。

图4 加工示意图
加工后小孔尺寸在φ3.99~3.995mm,加工表面光亮,符合加工要求。
5 中心孔定位方法
5.1 转台式
转台式保证千分表固定不动,工件绕轴线进行回转。将心轴与工件固定在CNC分度盘上,分度盘回转误差为0.018mm。转动分度盘,对转子垂直轴线的某一截面外表面进行圆跳动测量,选取外轮廓均匀分布的点进行记录,标注最大跳动量所在方向及最大跳动的垂直方向,以两个方向的中点作为中心孔的位置。转台式测量原理如图5所示。
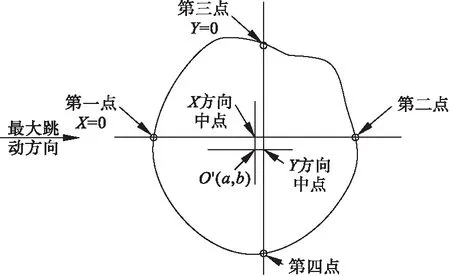
图5 转台式原理图
测量时,以工件X负方向测量点的横坐标作为X方向原点,Y负方向测量点的纵坐标作为Y方向原点。表1为转台式测量的转子中心点坐标及加工后转子的外圆径向跳动量。
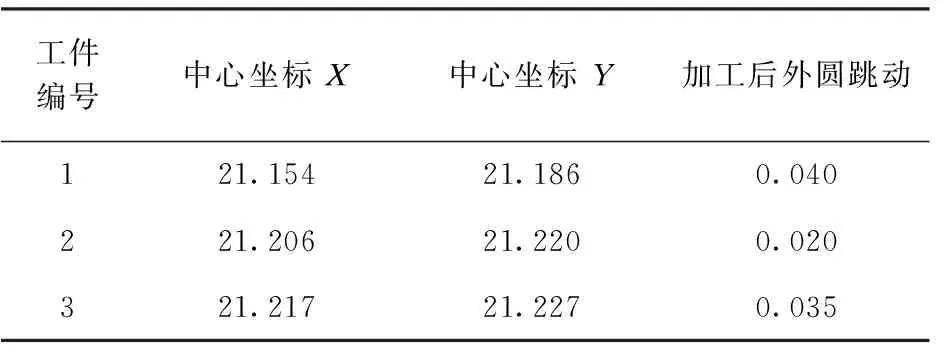
表1 转台式 mm
根据表1实验结果显示,转台法确定转子中心坐标变化较大,且加工后外圆跳动数值不稳定,部分试件超差。转台法在一定程度上减小了中心孔与该截面轮廓的径向跳动,但此方法具有很大的局限性,受多种误差影响精度;测量以外圆为基准,外圆与内孔存在偏心误差;内孔与心轴存在安装误差;心轴与分度盘回转中心存在偏心误差;以及分度盘自身存在回转误差;且不排除工件轮廓尺寸局部变化过大所带来的随机误差;以及中心孔加工时的加工误差。多种误差叠加,很难保证加工的位置精度,加工后的工件部分超差,加工结果比较随机。
5.2 转轴式
转轴式保证工件不动,千分表随机床主轴旋转绕工件转动。这种方法是利用普通转轴式精密圆度仪的工作原理确定加工位置,其主要原理是忽略孔加工时刀具摆动带来的误差,主轴旋转时对工件打表正是模拟工件加工后检测外圆跳动保证在0.03mm以内。
测量时,调节主轴X、Y向位置,保证主轴旋转一周,工件该截面圆跳动在规定的误差范围(0.03mm)之内,此时主轴位置即为中心孔的加工位置。转轴式测量原理如图6所示。
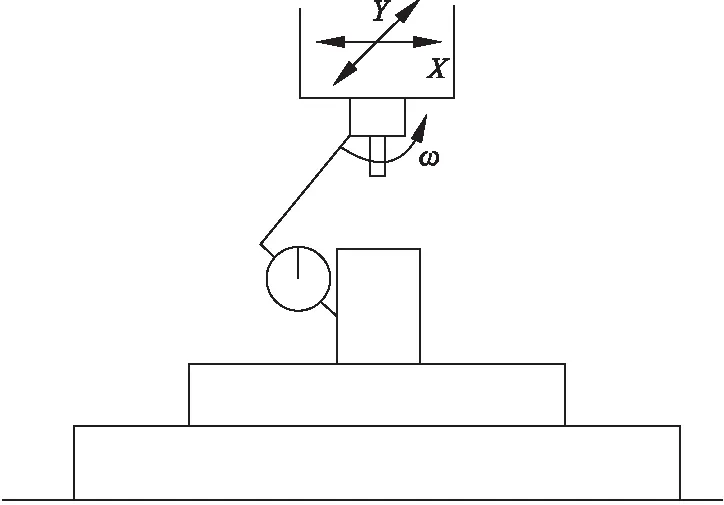
图6 转轴式原理图
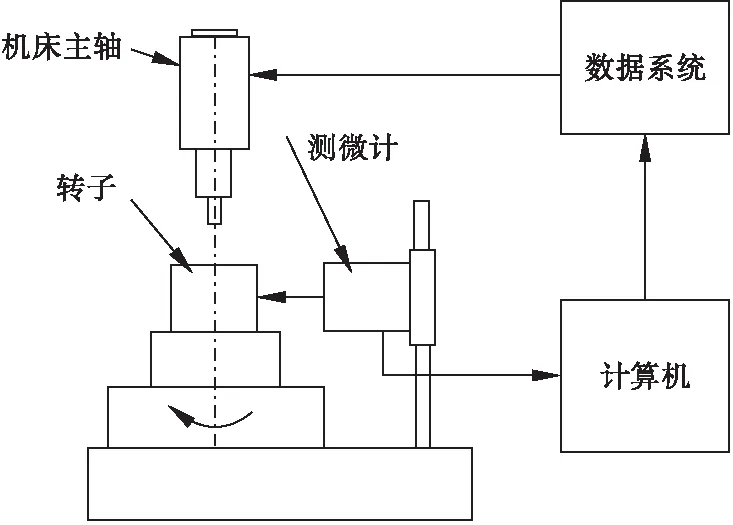
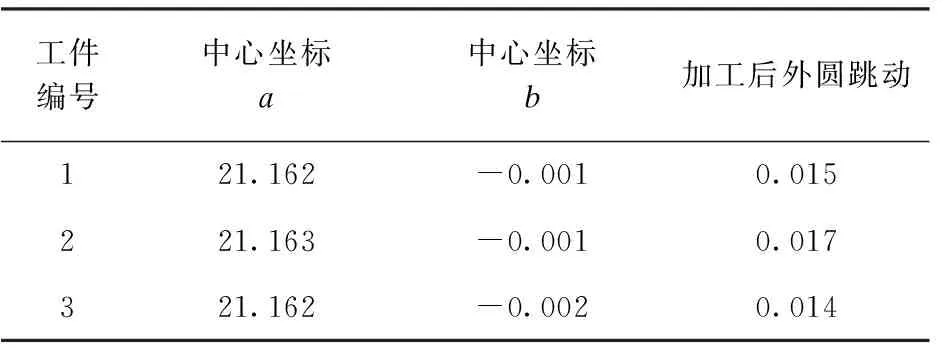
表2为转轴式加工前后同一截面转子外圆径向跳动量。
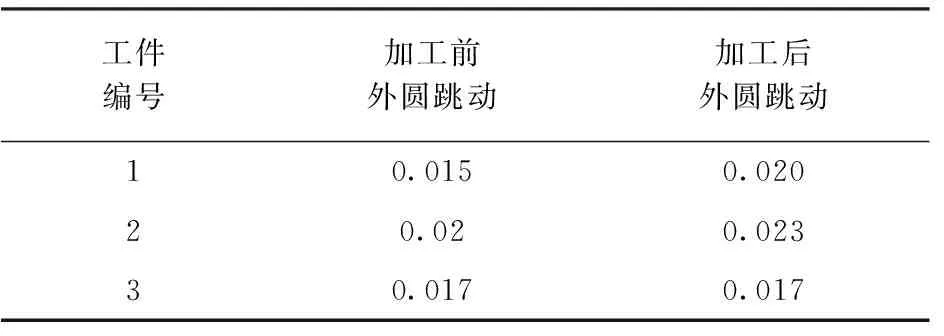
表2 转轴式 mm
根据表2实验结果可得:加工后由于加工机床主轴存在回转误差,因此加工后外圆跳动略大于加工前,加工试件均达到加工要求。相对于5.1方法,此方法的优点是:机床主轴旋转精度较高,不受表面形状复杂程度和工件安装误差的影响,导致加工出的中心孔位置精度更高,在一定程度上减小误差复映;测量步骤简单,不需要采集仪器及数据软件计算的配合。缺点是:虽然能保证中心孔的位置在要求范围内,但手动调整所用时间长,中心孔的位置在范围内相对随机,无法确定孔的最优位置。
5.3 最小二乘法(LSM)
圆度误差是指在回转体同一横截面内被测实际圆对其理想圆的变动量,是检测圆柱度、同轴度等其他误差的基础;其误差值大小直接影响回转体零件的互换性、装配精度、回转精度等,是保证零件质量的重要指标之一[10]。
最小二乘法是圆度误差评定方法中使用最普遍的一种,其理论较成熟,精度也较高[11]。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小[12],因此可以利用最小二乘圆的圆心作为加工孔的位置。主要判定方式如图7所示。O为工件实际轮廓原点,O′为最小二乘法的圆心,R为最小二乘圆半径。
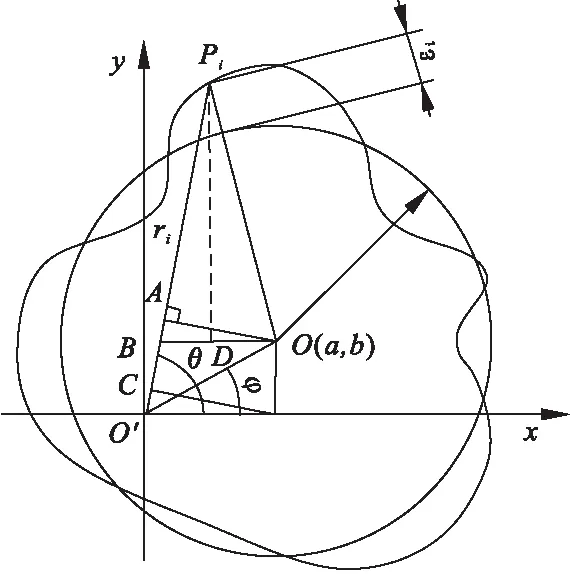
图7 最小二乘法原理图
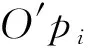
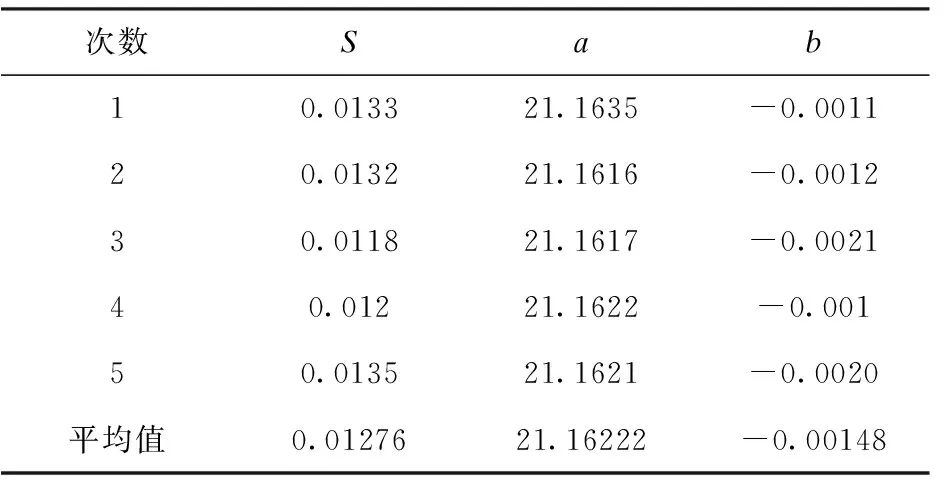
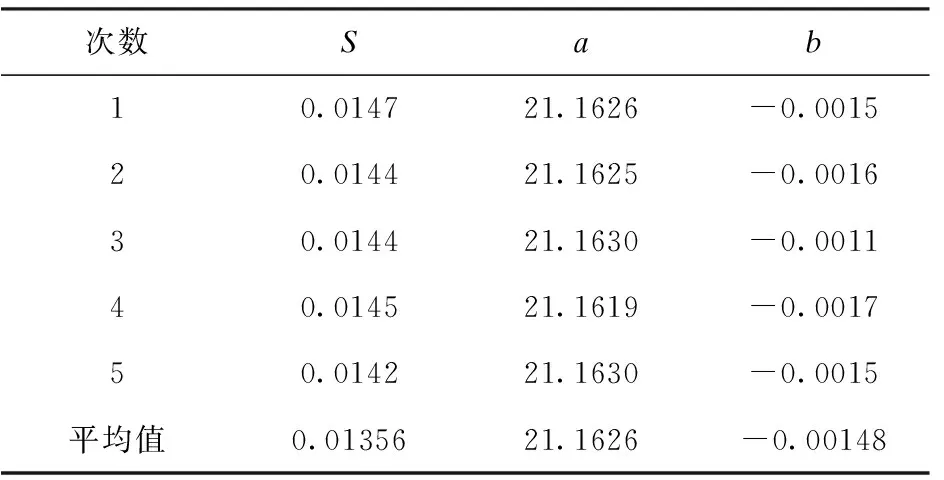
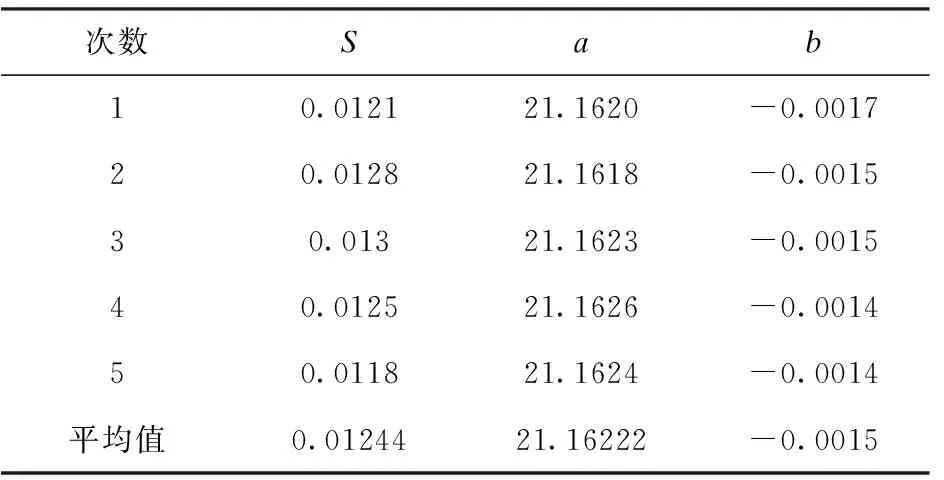
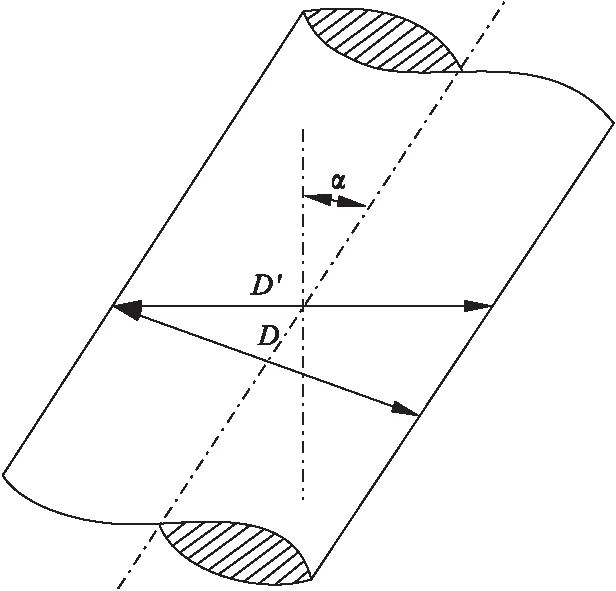
由于e< εi=ri-R-ecos(θi-φ) (1) 式中:εi为Pi到最小二乘圆的径向偏差。 (2) (3) O′保证距工件轮廓各点的平方和最小,因此可以作为加工中心孔的位置。 利用测微计进行数据采集,本文选用的测微计型号为CW-341,显示盒型号为5011-002。测微针分辨率达到1μm,重复定位精度1μm,精度高,定位准确,可以保证测量的准确性,符合实验要求。将测微计测头安放在测量架上,转子在微调系统的支配下安放在确定的位置随精密转台转动(精密回转台回转视为理想圆)。将测得的数据经最小二乘法计算,把计算的数据传输到机床的数控系统中,控制机床主轴的加工位置,实现测量—定位—加工一体化。测微计测量转子外轮廓装置如图8所示。 图8 测微计测量装置 利用Matlab对数据进行最小二乘法圆的拟合,为保证较高的重复精度,采取多圈采样,本实验采取圈数为5,S为圆度误差,最小二乘圆圆心坐标(a,b),并 取5次测量的平均值作为加工位置的机床坐标。表3~表5为3个转子试件5圈采集的数据,通过最小二乘法求得的最小二乘圆圆心坐标及圆度误差。 根据表3~表5数据求得每个试件的五组最小二乘圆圆心坐标和圆度误差值,分别对五组数据求平均值,将圆心坐标的平均值作为加工时的机床加工位置坐标。由于机床坐标精确至0.001,因此求得坐标值保留小数点后三位。 表3 转子1 mm 表4 转子2 mm 表5 转子3 mm 表6为3个转子加工位置坐标及加工后的外圆跳动。 表6 最小二乘法 mm 根据表6实验结果可知:加工后的转子外圆跳动均达到加工要求,且跳动范围相对稳定,证明最小二乘法确定转子中心孔位置精度更高。通过实验结果的对比显示,加工后外圆跳动量略大于最小二乘法求得的圆度误差平均值,误差主要取决于(1)精密的测量仪器精度与加工机床精度不同,加工时,机床定位坐标精度低于测量计算时的精度,导致实际加工位置与理论位置有偏差;(2)加工时,机床主轴回转精度、刀具安装的垂直精度、加工过程中产生震动等,都会导致加工孔的位置与计算位置出现偏移误差;(3)检测方法不同,圆度误差采用精密仪器精确测量,加工后转子外圆跳动采用千分表测量,手动测量产生误差。 加工后,转子外圆跳动符合加工要求,且孔的位置精度更高,同一批次转子加工后外圆跳动相对稳定。 安装时,转子轴线与工作台不垂直,设轴线与垂直方向的夹角为α。测量时,由于轴线的倾斜,垂直于回转轴线的横截面为一椭圆,其长轴为D′,转子的直径为D。由图9可知 D′=Dsecα (4) 产生的直径误差f为 fmax=D′-D=D(secα-1) (5) 图9 转子轴线倾斜示意图 根据实验实际测量,转子直径D在φ42.25~ 42.40mm之间,转子轴向垂直跳动不超过0.03mm,转子轴向长度约21mm。 安装倾斜角α不超过0.082°。将D=42.4、α=0.082代入公式(5)得 f=0.000041 故轴向倾斜误差影响很小,实验中可以忽略。 通过夹具的设计、工件的调整、定位方法的选择及误差分析,保证了磁性转子孔的位置精度。实验结合了传统打表的方法、测微计数据采集、圆度误差分析等方法进行数据对比。实验结果表明:转轴法和最小二乘法能有效保证中心孔的加工精度。实验条件允许的条件下,最小二乘法的精度更高。在工厂或实验条件不足的情况下,转轴法可用作代替测微计进行工件中心位置的确定。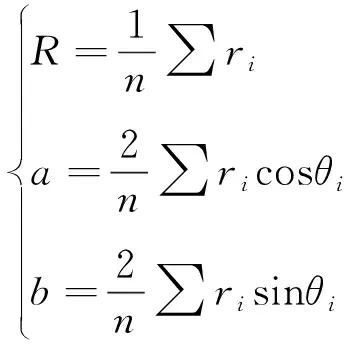
6 轴向倾斜误差分析
7 结论

