转子碰摩故障动力学仿真及实验验证

卢子乾,魏永合,矫晶晶

(沈阳理工大学 机械工程学院,沈阳 110159)

转子系统碰摩作为机械故障的主要原因之一,决定着设备的使用期限及寿命。转子系统的运行是一类非常复杂的动力学行为,碰摩过程也是一种非光滑、非线性问题。引发转子系统碰摩故障的原因很多,如不对中、不平衡、松动、裂纹、间隙过小、温度变化和流体导致的自激振动等。因此,描述转子系统特征的系统模型和描述碰摩过程的动力学模型也将不同。合理地建立碰摩转子系统的动力学模型,在此基础上采用数值仿真的分析方法,研究转子系统在碰摩发生时的振动特性及分岔等现象,能够揭示转子系统的运动规律,改善系统的动力学特性,为设备安全、稳定运行提供技术保障,为转子系统故障诊断和优化设计提供理论依据。

近些年来,国内外许多学者将研究重点置于 非线性转子故障领域,研究并发现了在不同故障转子系统中存在的分岔和混沌运动特性[1-2]。侯兰兰等对一类转子系统进行了非线性动力学分析,研究了偏心量取中等值时系统运行状态最丰富,刚度增大会使分岔复杂化,阻尼增大会抑制分岔过程[3]。目前转子系统中有关单盘转子方面的研究已很完善,但对于双盘转子的研究还存在缺陷,尤其是有关油膜力支撑下的双盘转子方面还有待于研究。

在研究非线性转子系统过程中,实验分析方法起着至关重要的作用[4]。实验研究方法不仅可以验证数值结论的一致性和理论模型分析结果的准确性,还能为进一步求解非线性问题提供依据和思路。袁惠群等通过对碰摩转子系统进行数值仿真和实验对比,论证了新模型的正确性,分析了系统的非线性特性以及速度影响系数对系统响应的影响[5-6]。王正浩等将数值仿真与实验验证相结合,研究了考虑轴承和隔振垫弹性的非对称支撑转子系统的非线性动力学响应特性[7]。

本文通过搭建与仿真同等条件下的实验转子实验台,进行相关转子-轴承系统的故障实验研究,收集实验数据,并对数据进行处理分析,用实验结果验证理论仿真结果,以获得碰摩故障的具体影响因素,证明模型建立的准确性,为转子-轴承系统的设计修正和故障识别提供参考依据。

1 双盘转子系统动力学研究

1.1 模型的建立

建立单跨双盘转子系统模型,如图1所示。

轴承左侧采用滑动支撑,右侧采用油膜力作用下的轴承支撑;两圆盘安装在一根无质量弹性轴上,分布在B点和C点处;为研究非线性油膜力的作用,将系统部分质量集中到轴瓦轴颈处,即各轴段质量等效分布在两圆盘中心和两端轴承中心,忽略轴系扭振和系统所受的陀螺力矩,只研究系统的横向振动。轴承两侧集中质量分别为m1、m4,左端圆盘质量为m2,右端圆盘质量为m3,c1为转子在轴承处的阻尼值,c2为左圆盘的阻尼值,c3为右圆盘的阻尼值,轴承宽度为L,转轴横截面半径为R。

图1 转子系统模型图

1.2 碰摩力的选择

转子的碰摩力模型如图2所示,PN和PT分别为碰摩中沿直径方向和切线方向所受的力,φ为转子的位置角。

图2 碰摩力模型

摩擦力满足库仑定律,可表示为

PN=(e-δ)kc
PT=f×PN(e≥δ)

(1)

(2)

将式(2)进行转化可得

1.3 非线性油膜力的选择

理论分析中采用经典的Capone圆轴承理论[8],该模型精度较高,短-圆轴承模型油膜力表达式为

(3)

式中:x、y分别为轴承处的位移;ω为系统转速;μ为润滑油粘度;p为圆盘转子质量的一半;α为油膜的起始动态边界角;V为速度对油膜力的影响参数;W为重力对油膜力的影响参数;S为碰摩力对油膜力的影响参数。

1.4 微分方程的建立

设转子左端轴承处位移为x1、y1,左转盘和端转盘处位移分别为x2、y2和x3、y3,转子右端处位移为x4、y4。根据牛顿第二定律,系统的动力学方程为

则系统无量纲化后的运动方程为

2 系统数值仿真及分析

为透彻分析油膜力支撑下的双盘转子系统动力学特性,本文通过改变不同参数,研究系统所呈现的运动学状态。转子系统的基本参数见表1。

系统所涉及的基本参数按表1选取,利用四阶龙格库塔法对无量纲化后的方程进行数值积分求解,在这里计算100个周期,由于系统开始时处于非平稳状态,故舍去前50个周期,只选取最后50个周期的计算结果,这样能确保系统处于稳定状态,且获得精确结果。

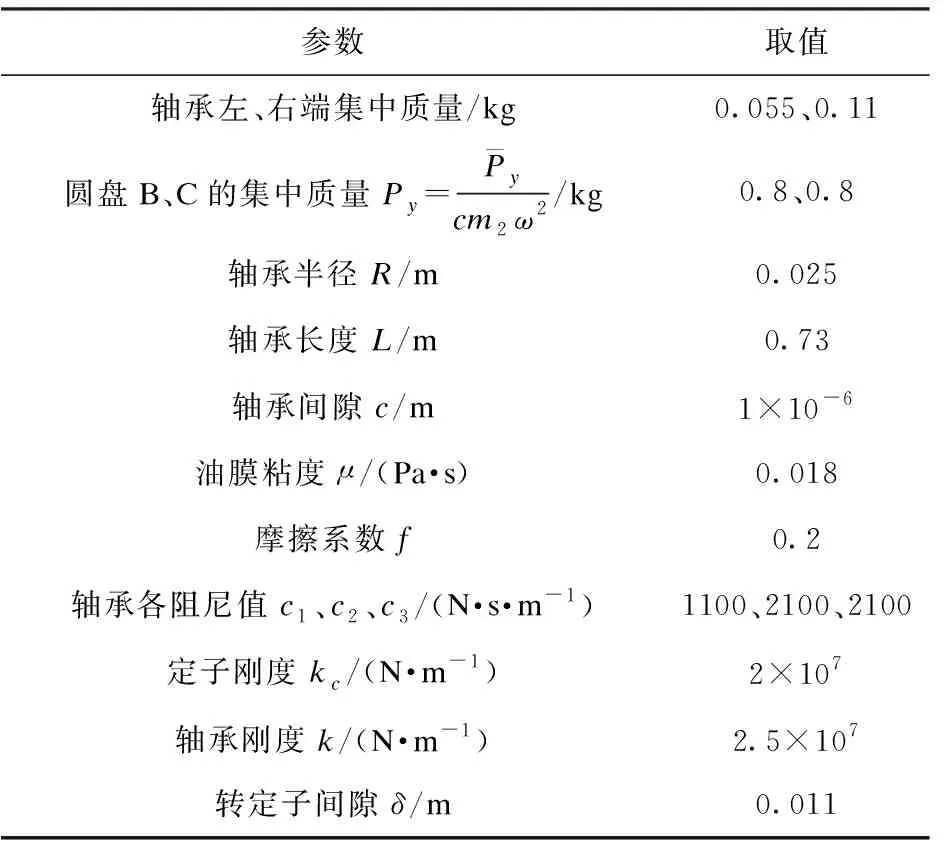
表1 转子系统的基本参数

使用分叉图作为系统稳定性的判别依据,选择转速作为分岔参数,通过计算得出轴承A点处x位移振动的分岔图,如图3所示,图中纵坐标是位移x0相对于轴承间隙c的无量纲值,即x0=x1/c;横坐标为系统转速ω。根据图3可知,在转子转速发生改变的条件下系统经历单周期→多周期→混沌→多周期→周期的复杂运动过程。图4分别为转子系统在转速为300rad/min、800rad/min、1400rad/min、2200rad/min时的时域图以及振动频谱图。

图3 系统随转速变化的分叉图

转子系统的固有频率为25Hz,临界转速约为1900rad/min。从图4可以看出,当系统转速在300rad/min时,振动幅值不大,且频率主要集中在3Hz左右,转子系统未发生碰摩,系统未因油膜力作用出现非线性振动特性,系统做稳定的周期运动。

图4 不同转速仿真时域图及振动频谱图

当转速到达800rad/min时,系统发生倍周期分岔,时域图发生轻微的削波现象,振幅不大;频谱图上出现低频成分,频率主要集中10Hz左右;此时系统发生碰摩,但碰摩力较小,系统处于简单的非线性振动,做周期运动。

当转速在1400rad/min时,系统到达多周期运动。系统随着碰摩力的逐渐增大,频谱图出现高阶频谱,且存在连续的频谱带,频率主要集中18Hz左右。随着系统油膜力及碰摩力的增大,系统的频率也在增大,碰摩故障加重。

当转速到达2200rad/min时,系统经历多周期到达混沌运动。频谱图中存在基频及高阶频谱,且存在连续的频谱带,频率主要集中25Hz左右。随着碰摩力、油膜力、振幅、偏心力的逐渐增大,系统的频率也在增大,碰摩故障严重。

当转速大于2200rad/min时,系统做概周期运动,回归相对稳定的运动状态。

3 设计实验并验证

实验设备采用本特利RK-4转子实验台,如图5所示。

直流电动机作为系统动力来源,电机经过联轴器驱动转子系统。实验采用涡流位移传感器进行数据测量,转轴处安装一对成 90°分布的传感器,用于测量x和y方向的振动信号;电动机输出轴处安装一只传感器,为转速调节器提供反馈信号。采集信号选用杭州亿恒科技公司生产的MI-7008i信号采集仪。整个转子实验台系统运行稳定,可在 0～10000rad/min范围内进行无级调速。通过设计实验,选取采样频率2560Hz,采样点数2048个。分别收集转子系统在转速为300、800、1400、2200rad/min时的振动位移信号,画出转子系统的时域图、频域图及轴心轨迹图,如图6所示。

图5 RK-4转子实验台

从图6中可以看出:当系统转速为300rad/min时,时域图为不稳定的波形,轴心轨迹出现不规则圆环,频域图振动幅值不大,且频率主要集中在3Hz左右,开始出现非线性振动特性,系统仍稳定运行。

当转速在800rad/min时,时域图为稳定的波形,轴心轨迹出现圆环交叉现象,且为不规则圆环,说明转子系统发生了碰摩;频谱图出现了基频和高阶频谱,频率主要集中在12Hz左右。

当转速在1400rad/min时,时域图为稳定的波形,轴心轨迹存在圆环重叠现象;系统随着碰摩力的逐渐增大,频谱图存在低阶频谱、基频和高阶频谱,且出现连续的频谱带,说明碰摩转子系统因油膜力的作用产生了油膜涡动,频率主要集中在18Hz左右,系统处于多周期运动。

当转速2200rad/min时,系统经历多周期到达混沌运动。时域图上存在削波;轴心轨迹为多圆交叠;频谱图上存在油膜失稳频率、基频、基频的分数阶及高阶倍频,且存在连续的频谱带,高阶倍频突出,说明系统碰摩力增大,碰摩故障加重,系统做概周期运动。

通过实际测试结果和仿真结果的对比,可以得出:此模型参数下,当转速到达300rad/min时,系统产生碰摩,频率主要表现为低倍频成分,碰摩力随着系统转速的增加也逐渐增大。当系统转速到达1400rad/min时,系统出现连续的高阶频谱带,说明系统因油膜力支撑,出现了油膜涡动。

图6 不同转速的实验时域图及振动频谱图

综上所述,在此条件下建立转子碰摩系统模型,实测结果与仿真结果在主要频率结构和频率成分构成上具有很强的相似性,因此证明了所建立碰摩模型是正确的。随转速的上升,系统的基频和高阶倍频幅值逐渐增大,系统内转定子之间的碰摩故障愈演愈烈。

4 结论

提出了一种考虑非线性油膜力作用下的单跨双圆盘转子系统的非线性动力学模型,并对转子系统进行了动力学分析,得到了转子系统的动态响应特性。同等条件下设计了实验,通过对实验数据与仿真结果的对比,反映了此模型的合理性。本文所建立的单跨双盘转子碰摩模型为搭建转子碰摩实验台提供了一定的理论依据,结果证明了碰摩力及油膜力会对系统的动态响应产生很大影响,在对此类转子碰摩模型进行诊断分析时需加以考虑。