基于多模型IMC-PID的三水箱液位控制算法研究

纪振平,胡孙燚

(沈阳理工大学 自动化与电气工程学院,沈阳 110159)

液位是工业过程中的常见参数,具有便于直接观察和容易测量等特点[1]。三容水箱系统作为一种具有非线性、大惯性、时滞性的液位过程系统,可模拟许多具有复杂特性的工业过程,如:石油化工、冶金、食品灌装等。因此,对三容水箱进行液位过程控制系统研究,具有实际意义和潜在价值。

传统PID控制器具有结构简单、便于理解、易于实现等特点,常应用于一些简单的工业过程控制中,且控制效果良好。随着人们对具有非线性、大惯性、时滞性等复杂特性的工业过程的控制需求的不断提高,虽然多数情况下传统PID控制器也能基本实现过程控制,但往往会使系统的性能指标很差,有时还会导致系统不稳定。

20世纪70年代以来,许多专家学者在致力于先进控制策略研究的过程中,提出了大量的针对复杂工业过程的先进控制算法。其中,内模控制(IMC)是一种基于过程数学模型进行控制器设计的新型控制策略,由于其结构简单、便于计算和调节、鲁棒性强、适用于大滞后系统等特点,自提出之日起,便受到了控制界的普遍关注,经过大量的科学理论研究和现场实践测试讨论,证明了内模控制的有效性[2-5]。

针对具有较为复杂特性的三容水箱液位过程系统,国内外研究人员也进行了多种不同控制策略的尝试,并从一定程度上改善了系统的性能指标。Joseph C等人提出了一种模型预测控制算法[6];李玉娇设计了一种模糊PID 控制器[7];杨天奇提出了一种无模型自适应控制算法[8]。本文则从提高模型匹配程度和改善控制器性能的角度,提出一种基于多模型切换的内模PID控制策略,从一定程度上改善了系统的性能指标。

1 多模型建模

1.1 建模区间划分

选择合适的间距调节调节阀开度u,取一些能大致覆盖工况范围(即液位高度h0～180mm)的点,并记录下调节阀开度与对应的液位高度,这里用系统开环放大系数K值的变化大小来表示模型的非线性程度,数据如表1所示。

过程模型开环放大系数K与液位高度h之间的关系如图1所示。

表1 不同工况下的K值

由图1可以看出,在工况范围内,随着液位高度的增加,系统开环放大系数K值也不断变大,即过程模型的非线性程度在不断变化,且两者的关系近似成一定比例。因此,可以按照液位高度来划分多模型建模区间,在每个区间内建立各自的局部线性模型,来拟合全局的非线性模型。

图1 非线性程度变化曲线图

1.2 模型结构

在水箱液位过程模型结构的获取上,一般利用物料平衡原理,采用机理法建模,经过简单的数学推导,可得出常见的单容水箱液位过程数学模型。

(1)

式中:K、T和L分别为单容水箱液位过程的开环放大系数、时间常数和时滞时间；s表示该模型为连续模型。

本文被控对象为三容水箱,液位过程数学模型则可表示为

(2)

为方便内模PID控制器的设计与实现,可将高阶模型进行等效降阶处理。因此,在保证模型拟合效果良好的前提下,实际模型辨识过程中将采用一阶时滞模型来拟合该三阶时滞模型,即辨识所用模型为

(3)

实际利用计算机进行系统参数辨识和液位控制时采用的都是离散系统模型,因此,需利用连续系统离散化的方法在Matlab中对该一阶时滞连续模型进行离散化处理,采样周期设定为1秒。

1.3 模型参数

1.3.1 测试输入/输出数据

在开环情况下,对三容水箱进行实际系统特性的测试。通过设定调节阀开度变化,依次在划分的多个模型区间内采集输入/输出数据对{u(k),y(k),k=1，2,…,n},长度为n。

1.3.2 模型参数辨识

(a)最小二乘算法辨识

最小二乘法(LS)是一种常用的参数辨识算法。这里利用批处理最小二乘法,对于采集的n组输入/输出数据对{u(k),y(k),k=1，2,…,n},取性能指标函数

(4)

在Matlab中绘制出辨识所得模型响应曲线,并与采集的实际模型响应曲线进行对比,如图2所示。

图2 辨识模型与实际模型的响应曲线图

由图2可以看出,利用最小二乘算法辨识所得模型的过程响应曲线与实际响应曲线大致吻合,表明最小二乘算法对模型参数辨识有一定准度,但不太精确。

(b)粒子群算法辨识

粒子群算法(PSO)是一种新型的仿生算法,具有实现容易、精度高、收敛快等优点[9]。以批处理最小二乘法获得的参数为基准,选择合适的参数范围,利用改进的粒子群算法再次对模型参数进行辨识。这里采用模型输出的均方误差作为参数辨识的目标函数,具体描述如下:

(5)

在Matlab中绘制出辨识所得模型响应曲线,并与采集的实际模型响应曲线进行对比,如图3所示。

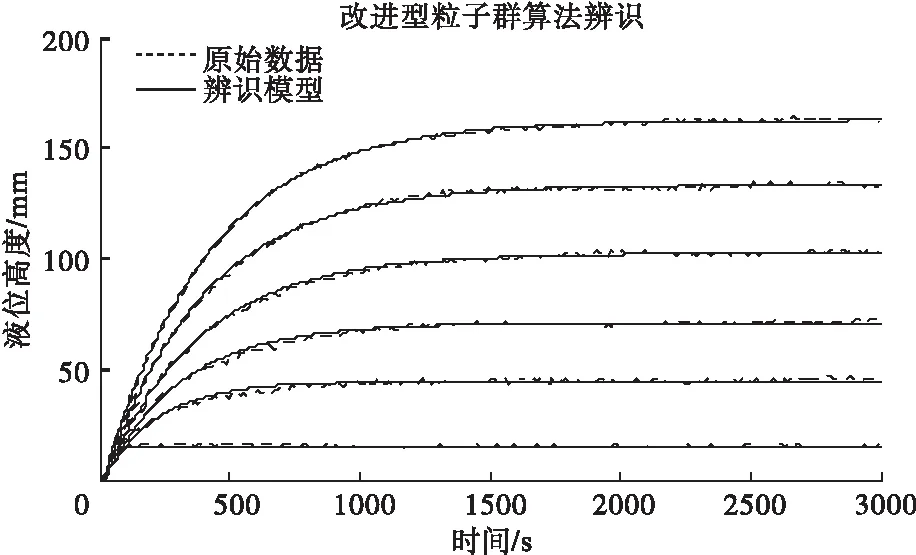
图3 辨识模型与实际模型的响应曲线图

由图3可以看出,利用改进型粒子群算法辨识所得模型的过程响应曲线与实际响应曲线吻合程度极高,表明在最小二乘法辨识的基础上,再次对模型参数利用粒子群算法进一步辨识的有效性。

2 内模PID控制器设计

典型的内模控制结构图如图4所示。

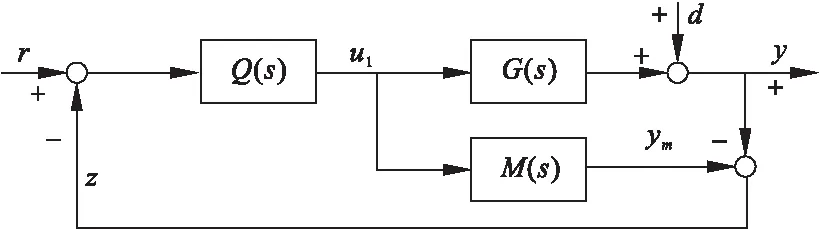
图4 内模控制原理结构图

图4中,G(s)为被控过程;M(s)为被控过程的数学模型;Q(s)为内模控制器;r、y和d分别为给定值、输出值和扰动信号;u1、z和ym分别为控制信号、反馈信号和模型输出信号。内模控制的目标是使输出值y逼近给定值r。

根据系统结构图的等效变换原则,可以将图4等价变换为图5所示的经典反馈控制形式,虚线框内相当于经典反馈控制系统里的反馈控制器C(s),其输出为控制信号u2,z相当于反馈信号。

图5 等效反馈控制系统结构图

图5中,u2为反馈控制器C(s)的输出信号。为确保系统的稳定性和鲁棒性,在内模控制器Q(s)中引入一个低通滤波器f(s)=1/(λs+1),λ为滤波器时间常数。

对于拟合的一阶时滞三容水箱模型(3)，按照IMC-PID控制器设计原理,经过一系列数学推导,最终可得转换后的PID控制器参数为

(7)

由式(8)可以看出,IMC-PID控制器参数只与被控对象参数K2、T4、L2及滤波器参数λ有关,因此只需设定合适的滤波器参数λ,既可获取较优的PID控制器参数。

3 仿真结果与分析

选取几个在全工况范围内(即液位高度0～180mm)比较有代表性的液位高度设定值,分别为45mm、105mm和165mm,采用经典PID和多模型IMC-PID两种不同的控制方法在Matlab中进行仿真对比,见图6(仿真图右上角显示的是放大后的部分细节)。

由Matlab仿真实验可以看出:经典PID和多模型IMC-PID控制下的液位过程响应曲线的上升时间基本一致;不同之处在于:(1)当给定液位高度为45mm时,经典PID控制下的液位实际值很难快速平稳地跟踪上给定值,系统静差消除时间很长;而多模型IMC-PID控制则可以快速平稳地跟踪上给定值。(2)当给定液位高度为105mm时,经典PID控制虽然也能获得还算良好的动态性能;但多模型IMC-PID控制下的液位系统超调量更小、调节时间更短、振荡次数更少,明显优于经典PID控制。(3)当给定液位高度为165mm时,经典PID控制下的液位过程响应曲线出现了近似等幅振荡的趋势,很难跟踪上给定值;而多模型IMC-PID控制在保证系统稳定性的同时,仍然可保证较小的超调量、较短的调节时间和较少的振荡次数等动态性能指标。

图6 三容水箱液位过程响应曲线Matlab仿真图

4 结论

对于三容水箱液位过程系统,利用多模型方法建立多个局部线性系统模型,较大程度地拟合了全局非线性系统模型;通过对比辨识模型与实际模型响应曲线的吻合程度,表明了粒子群算法对三容水箱的模型参数辨识更为有效;内模PID控制器不仅参数易于整定,还便于相关操作人员对其控制过程的理解与后续的调试。从Matlab仿真中可以看出,基于多模型IMC-PID的控制算法在全工况范围内(即液位高度0～180mm)的总体控制效果明显优于经典PID控制,表明基于多模型IMC-PID的控制算法在对三容水箱液位过程系统控制上的有效性。