基于SimMechanics的工业机器人刚度分析
陈晓菲,舒启林,李文韬
(沈阳理工大学 机械工程学院,沈阳 110159)
近年来,随着工业技术的进步,工业机器人得到了飞速的发展,应用也更加广泛。工业机器人在加工过程中可以多轴联动,工作范围大、动作灵活,可以实现多维运动[1]。但是,由于工业机器人自身的结构弱刚性,在外力作用下易发生变形,影响末端定位精度,有必要对工业机器人进行刚度分析。为了防止工业机器人超出工作区间或到达奇异位置,在刚度分析之前先求解机器人的工作空间。
工作空间的大小代表了工业机器人的活动范围,是表征机器人工作能力的一个重要指标。工作空间的大小是由机器人的几何形状和关节运动的限位决定的。目前工作空间的计算非常复杂,解法主要有解析法、图解法和数值法[2-3]。解析法是通过多次包络的方法来确定工作空间,解算过程十分繁琐并且不够直观;图解法虽然比较直观但是对于关节数较多的机器人很难求解;数值法应用比较广泛,最有代表性的就是蒙特卡洛法,不过运算量比较大,需要建立机器人的数学模型并进行运动学求解。本文采用基于Matlab仿真法,利用Simulink中的SimMechanics模块进行建模求解。该方法无需建立复杂的数学模型,无需求解传统的运动学方程,也不需要进行复杂的编程操作即可实现实时的结果分析。
动力学分析软件有很多,但是SimMechanics集成在Matlab上,数据处理功能强大,可以与solidworks端口连接,大大缩短建模时间。SimMechanics建模方便直观,可以在模型中改变结构、优化系统参数,在仿真环境中分析结果[4-5]。可以将系统模块在simulink窗口中组合、连接成各种机构,并且通过检测和传感器模块与simulink基础模块连接,得到整个系统的仿真结果。用这种方法分析机器人刚度,克服了传统方法中对机器人进行运动学求解的弊端,同时规避了利用极限理论编程运算的复杂[6]。
1 工业机器人的几何参数
本文研究的工业机器人共有6个关节,关节i位于前后两个连杆之间。zi轴配置在关节i的轴线上,xi-1轴位于zi-1轴和zi轴的公垂线上。αi是绕着xi-1轴从zi-1轴旋转到zi轴的转角。θi是关节的转角范围,ai是沿着xi-1轴从zi-1轴到zi轴的距离,di是沿着zi轴从xi-1轴到xi轴的距离,具体的机器人连杆坐标系如图1,连杆参数如表1。
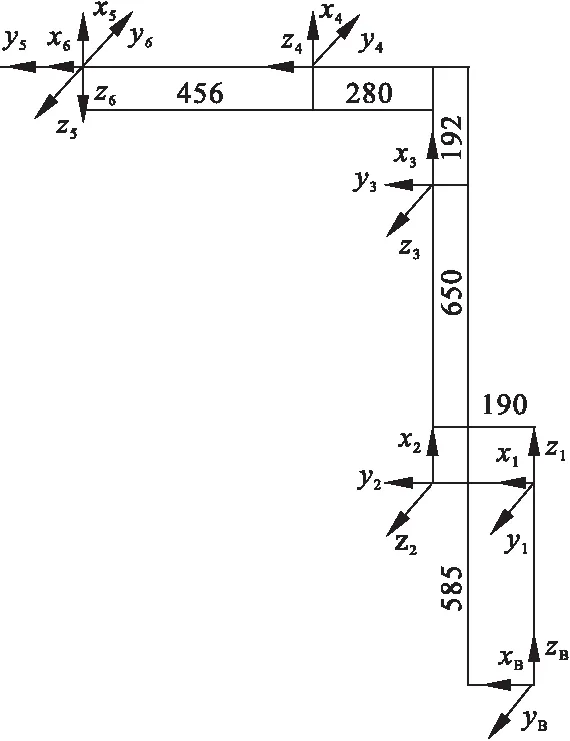
图1 机器人三维模型
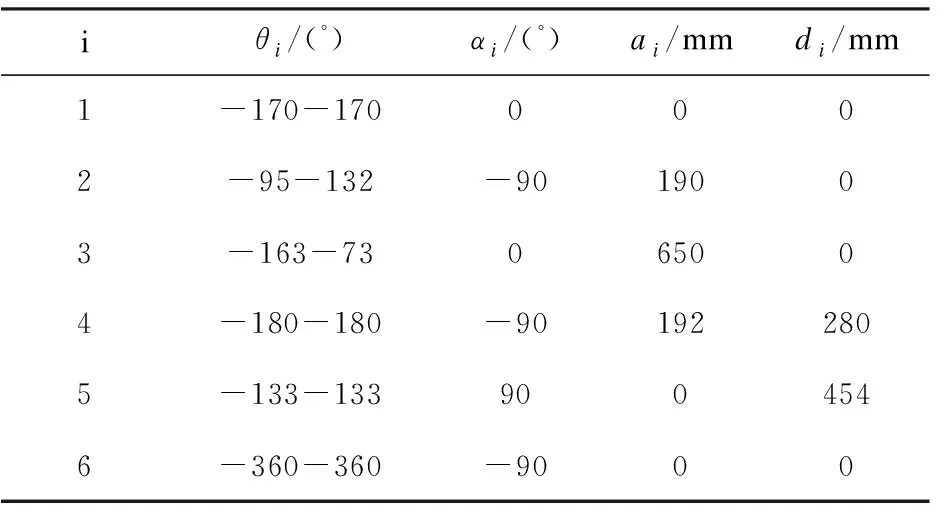
iθi/(°)αi/(°)ai/mmdi/mm1-170-1700002-95-132-9019003-163-73065004-180-180-901922805-133-1339004546-360-360-9000
2 机器人工作空间仿真模型
Solidworks为SimMechanics提供了插件接口,将对应版本的SimMechanics link插件安装到Matlab中与Solidworks相互关联。在Solidworks中构建工业机器人的三维模型,定义各零部件的材料属性,将三维模型导入到Matlab中转换成仿真模型,这种方法即减少人工建模的计算量,也避免了人工计算的失误,大大提高工作效率。转换后的仿真模型与三维模型中的配合关系有关,各零件间的传动关系均表现在仿真模型中,本文只研究各个连杆间的主要传动关系。仿真模型中的weld模块表示固联关系,对仿真结果没有影响。工业机器人的前3个关节决定机器人的活动范围,后3个关节决定机器人的姿态,因此只在前3个关节处施加驱动信号。工业机器人末端位置的数据通过simout模块输出到Matlab的工作区中,最终的仿真模型如图2所示。
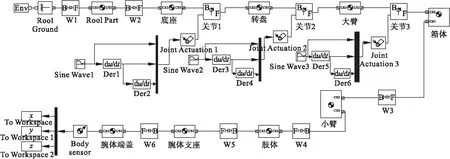
图2 工作空间仿真模型
模型中主要有3个关节驱动模块,驱动信号为正弦信号,根据各个关节的转角范围调整正弦函数幅值和偏置的大小,三个驱动信号的频率设置成不同的数值。每个驱动信号包含3个元素,分别是角度、角速度、角加速度,三者通过微分运算联系到一起。3个输出模块分别输出机器人末端x、y、z三个方向的位置坐标到工作区,在工作区直接利用3个变量,通过绘图语句绘制出工作空间的二维图和三维图如图3所示。

图3 机器人工作空间效果图
通过对输出的数据进行处理,得到机器人工作空间的三维图和工作空间的xoy平面投影图和xoz平面投影图。由于机器人关节1的转角范围是±170°,故xoz投影图并不是全部闭合的,而是有一处“缺口”。三维图中可以看到机器人空间上的最大工作范围,为了看清三维图内部的情况,将关节1的驱动信号调为0,便得到xoy平面的截面图,由此可见在三维图内部还有一部分区域不可到达。机器人的活动范围受关节角度的限制,机器人只能以特定姿态才能到达工作空间的边界位置,这些位置属于机器人的非灵巧空间。接下来的刚度分析以此为基础,在机器人的灵巧空间内做研究。
3 机器人刚度模型
机器人的刚度反映了机器人在外力的作用下抵抗位移的能力。机器人在不同位姿处的刚度称为机器人的操作刚度,为了求得机器人的操作刚度需建立关节刚度与操作刚度的映射模型。用弹簧系数ki来表示整个驱动系统的刚度,用τi表示关节力矩,Δθi表示关节变量,则有[7-8]
τi=kiΔθi(i=1,2,…,6)
(1)
F是一个6维力矢量,作用于机器人的末端,产生的变形为X,K表示机器人的笛卡尔刚度矩阵。当机械结构受力和变形都足够小时,可以认为两者近似满足如下的线性关系
F=K·X
(2)
JT(q)称为机器人的力雅可比,它表示在静平衡状态下,操作力向关节力映射的线性关系。机器人的力雅可比是运动雅可比的转置。运动雅克比矩阵J(q)的表达式是
(3)
忽略关节重力和摩擦力,根据虚功原理推导出关节力矩矢量τ和末端的负载力矢量F的关系为:
τ=JT(q)F
(4)
对公式(4)求导得到
dτ=(dJ(q)T)F+J(q)T(dF)
(5)
Kθ为其关节刚度矩阵,KC为补充刚度矩阵。联立式(1)、(2)、(3)、(4)、(5),化简得到如下关系式
J(q)TKJ(q)=Kθ-Kc
(6)
上式称为保守合同变换CCT,那么CCT的逆变换为
K=J(q)-T(Kθ-Kc)J(q)-1
(7)
刚度补偿矩阵Kc在负载力不是很大时可以忽略不计,有研究表明在机器人的有效负载范围内其值可以忽略不计。简化后得到下式
K=J(q)-TKθJ(q)-1
(8)
上式即为传统静刚度模型,末端变形量与机器人该位姿的刚度线性关系如下:
(9)
由上式可以看出,求解机器人刚度,需要分别求出各个位置处的作用力和变形量,作用力即为施加的负载力。那么,刚度仿真模型的最终目标便是求出各个位姿处机器人末端的变形量。
4 机器人刚度仿真模型
工业机器人的末端变形主要是由各关节处的传动引起的,传动部件由齿轮、转轴、皮带等组成,将这些传动部件的变形全部集中到各个关节上以简化模型,在模型中引用弹性阻尼来表示这些传动部件的综合作用。机器人刚度仿真模型的创建过程与求解工作空间时类似,模型中的六个转动关系分别对应工业机器人的六个关节,在机器人末端分别施加七组不同的载荷,负载方向和数值如表2所示(模型中的坐标方向为:y轴正方向与重力加速度方向相反,符合右手定则),在不同负载、不同位姿下得到机器人末端的x、y、z各个方向上的变形量,通过这些变形量来分析机器人的刚度,scope模块可以输出各个关节角度变化的图像。
本文研究的工业机器人有效负载是20kg,对工业机器人末端施加x、y、z三个不同方向的负载,并且依次只改变其中一个方向负载的大小,比较单方向负载的变化对机器人末端操作刚度的影响。本文的分析方法属于静力学分析,机器人的末端变形量很小,选取机器人末端的某一固定点,其初始位置坐标可以从模型中查到,施加负载后的位置坐标则直接输出到工作区中。仿真过程的步长自动选取,仿真完成后会得到多组数据,取平均值为最终坐标值。仿真过程中共取4种不同位姿,各个方向的具体变形量如表2所示。
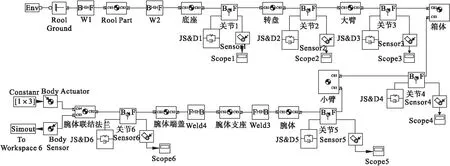
图4 刚度仿真模型
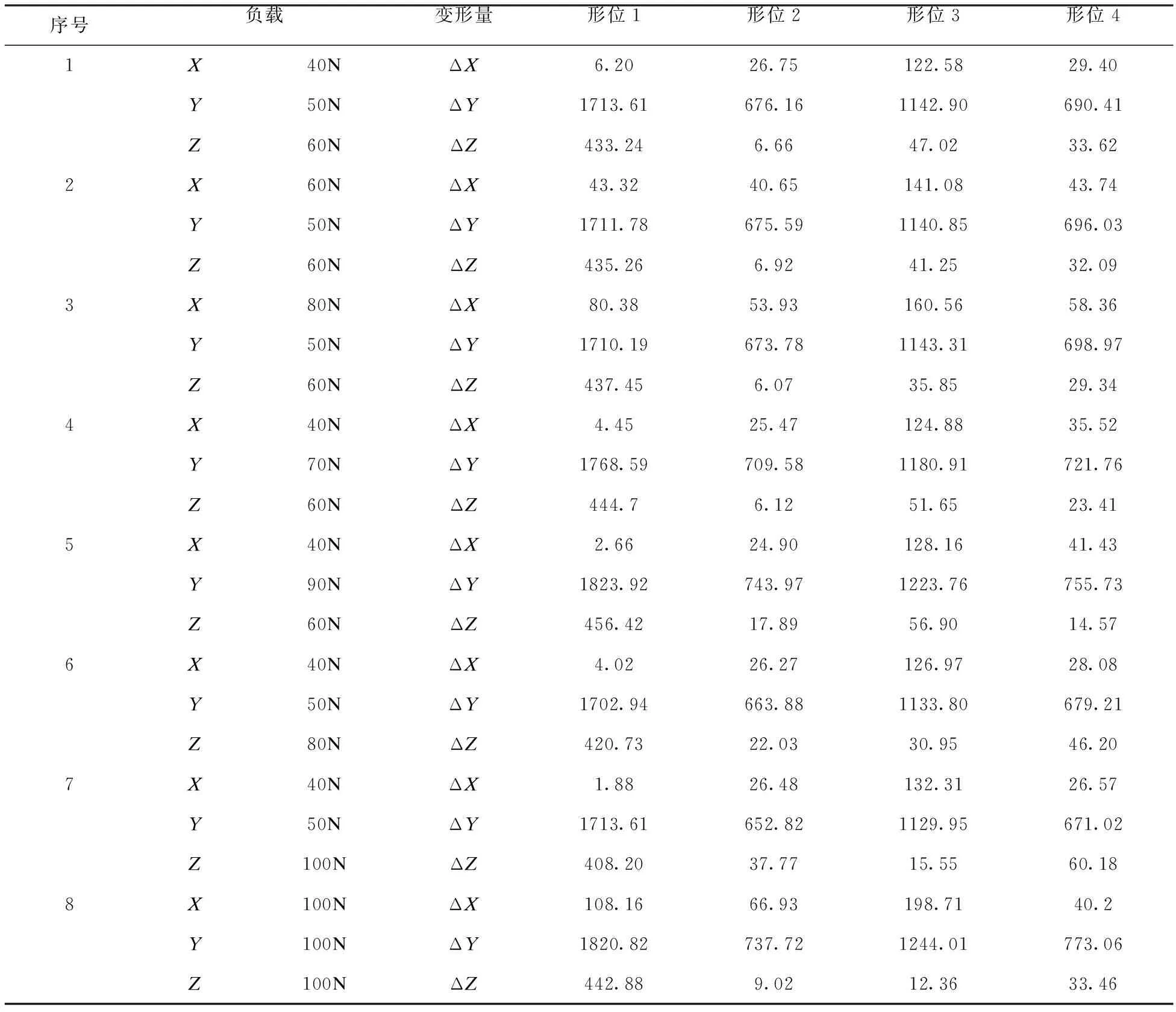
表2 机器人末端的变形量 μm
由表2的数据可知,同一负载下,不同位姿所产生的变形量也不相同,这说明机器人的位置和姿态对工业机器人的刚度有很大的影响。随着负载的增加,x、y方向上机器人末端的变形量逐渐增大,而z方向形位1和形位3变形量减小,形位2和形位4变形量增大,这是由于形位不同造成z方向负载力的作用效果不同,即对形位1和形位3而言是压力,对形位2和形位4而言是拉力。由于关节5和关节6的角度不同,机器人末端不是与y轴平行的,因此各个方向施加的负载力是相互影响的,不同形位各方向的影响情况不同。并且在三个方向上负载力大小相同时y轴方向的变形量最大,说明y方向机器人刚度较弱。由此可以得出,选取合理的加工位置和姿态可以改善机器人的结构弱刚性问题,提高工业机器人的加工质量。
为了进一步分析各个关节对工业机器人刚度的影响,引入刚度椭球指标来描述机器人末端力与变形之间的关系,由式(9)可知当机器人末端产生单位变形时即|X|=1,那么[9]:
XTX=1
(10)
将式(9)带入式(10),可以得到:
(11)
该式即为机器人末端的刚度椭球方程,令
(12)
忽略机器人末端的角度变化,令hij表示H的第i行第j列,fx、fy、fz表示刚度椭球的三个坐标轴。为简化计算,取椭球fx、fy两轴上的截距中较小的一个作为刚度评价指标,即:
(13)
确定机器人的一个固定位姿,取θ1=-30°,θ2=-30°,θ3=30°,θ4=45°,θ5=30°,θ6=-45°,分别只改变其中一个关节的角度,所取关节角度的间隔为10°,共11组即变化的范围都是110°,负载力的大小相同,仿真分析得出末端变形量并绘制出刚度指标与关节角度之间的关系图如图5所示。

图5 关节角度与刚度指标关系图
由以上数据,图5a反映出机器人的第一关节角度对机器人操作刚度没有影响,对比图5中刚度指标的变化范围,刚度指标受第二、三关节角度的影响较大,而第四、五、六关节角度对刚度指标的影响较小。由此可见为了提高机器人的操作刚度,二、三关节角度的选取更为重要。
5 结论
针对工业机器人的刚度辨识问题,提出了一种基于SimMechanics模块建模仿真的方法。该方法不需要建立机器人的运动学方程,可以直接根据机构的尺寸和传动关系进行建模和求解,大大减轻了计算的工作量。通过仿真分析得出机器人末端的坐标参数,通过数据处理和分析得到了机器人的工作空间,规避了机器人的奇异点。通过对末端变形量的分析,得出位姿和负载对机器人的操作刚度都有影响。根据刚度指标与关节角度之间的关系,得出第二、三关节角度对机器人的刚度影响较大,第四、五、六关节角度对刚度指标的影响较小,为进一步分析最优位姿做准备。

