基于天牛须搜索的花朵授粉算法
邵良杉,韩瑞达
辽宁工程技术大学 系统工程研究所,辽宁 葫芦岛 125105
1 引言
群智能算法是一种通过模拟或揭示某些自然现象或过程来解决优化问题的算法,如粒子群优化算法[1]、人工鱼群算法[2]等。花朵授粉算法[3](Flower Pollination Algorithm,FPA)是由Yang等人在2012年提出的一种模拟自然界开花植物授粉过程的群智能算法,该算法不需要知道待优化函数的具体形式,参数少,易实现,但该算法也存在寻优精度低、后期收敛速度慢等问题。近年来很多学者对FPA算法进行了研究改进和应用:卞京红等[4]将FPA与萤火虫算结合,自适应调整转换概率 p,并在局部授粉过程中引入自适应的变异因子;Zhou[5]等使用精英反向学习初始化种群,提高了初始种群的多样性;肖辉辉在文献[6]采用花朵个体间的万有引力和算法本身的莱维飞行共同实现个体位置的更新,在文献[7]中,在局部寻优部分对进入下一次迭代的较差个体采用单纯形法的扩张、收缩/压缩操作,提高局部寻优能力;段艳明等[8]通过引入量子系统的态叠加特性,用波函数描述种群个体的位置,提高算法的全局寻优能力;文献[9]利用高斯变异对FPA算法的全局搜索进行扰动,增强种群的多样性;文献[10]通过入侵杂草的繁殖、空间扩散和竞争策略,动态生成种群,增加种群的多样性和有效性。以上文献对FPA算法的寻优能力有一定程度上的改进,但很多改进算法存在时间复杂度过高,运行速度慢等问题。
针对花朵授粉算法的收敛速度和精度的问题,本文将天牛须搜索算法(Beetle Antennae Search,BAS)[11]引入花朵授粉算法的全局寻优阶段,天牛须搜索算法仅需一个个体,运算简单且能快速收敛,可以提高FPA算法的收敛速度。将一种变异策略引入局部寻优阶段,以提高算法跳出局部最优的能力。
2 花朵授粉算法
2.1 花朵授粉算法介绍
花朵授粉算法是一种模拟自然界开花植物授粉过程的群智能优化算法。在现实的自然界中,每一棵显花植物可以开多朵花,每朵花产生数百万甚至数十亿的花粉配子。为了使该算法更为高效,FPA对花朵授粉过程进行简化,每棵显花植物只开一朵花,且每朵花只产生一个花粉配子。一朵花或一个配子对应于优化问题中的一个解,并且每朵花都是通过转换概率p进行异花授粉操作,或以概率1-p进行自花授粉操作繁衍后代。异花授粉的范围较大,可以视为全局搜索;自花授粉的范围较小,可以视为局部搜索。
根据开花植物的授粉过程,花朵授粉算法总结出四条规律:
(1)异花授粉通过昆虫或鸟类携带花粉来进行,是一种全局授粉过程。
(2)自花授粉通过自然因素进行,是一种局部授粉过程。
(3)花粉的繁殖概率与涉及的两朵花的相似性成正比。
(4)转换概率p控制着全局授粉和局部授粉的相互转换。
2.2 花朵授粉算法流程及缺陷分析
2.2.1 算法流程
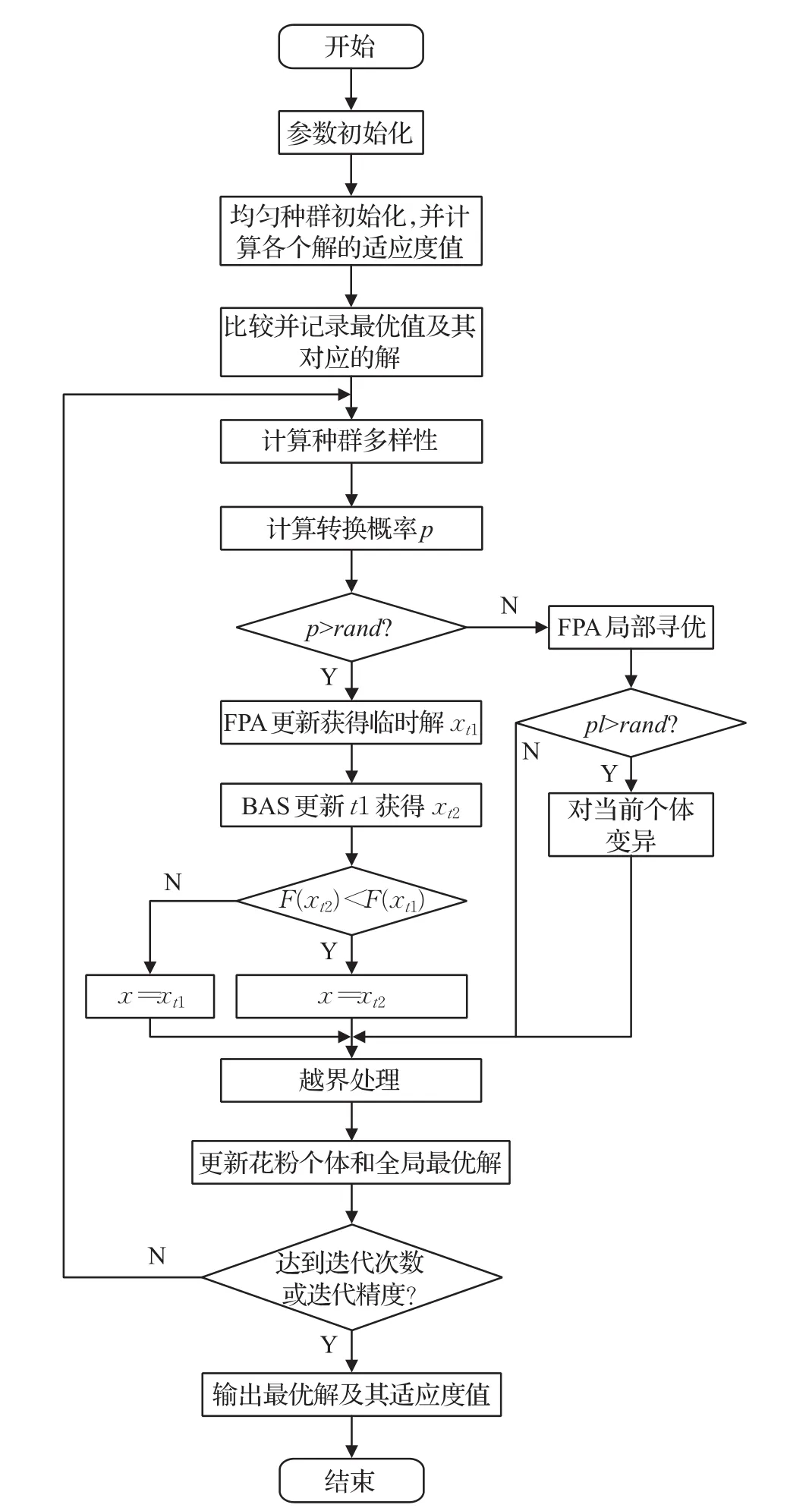
FPA的流程图如图1。
图1中公式(1)、(2)分别为:


其中,Γ(λ)是标准的伽玛函数,λ=1.5。
2.2.2 花朵授粉算法的缺陷分析
为验证FPA算法各部分的寻优能力和缺陷,设计以下实验验证FPA算法的全局寻优能力,局部寻优能力和跳出局部最优的能力。
设置种群数为20,迭代次数为1 000,维度为10,选取具有一定代表性的单峰函数Sphere和多峰函数Rastrigin,求最优值。单峰函数能检验算法的收敛速度,多峰函数能检验算法是否容易陷入局部最优和跳出局部最优的能力。

图1 FPA算法的流程
其中Sphere和Rastrigin函数的表达式如公式(4)、(5)所示:

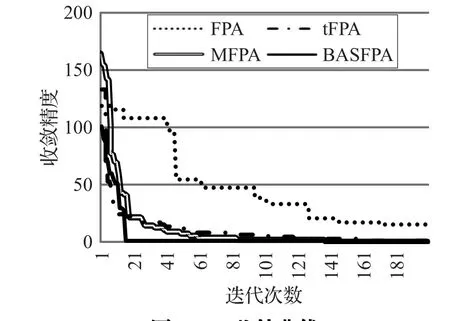
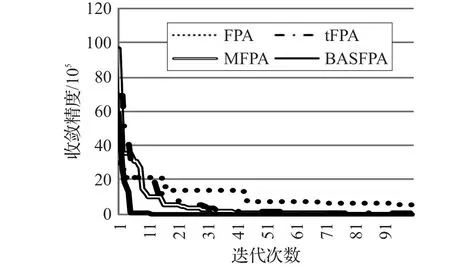
每个函数运行50次,统计其收敛曲线,从图2可以看出,FPA算法在前400次迭代收敛速度较快,而之后收敛速度很快降低,在900次迭代时收敛曲线几乎平行于x轴,说明FPA算法后期收敛速度较慢。图3中,经常有水平线段,说明算法陷入了局部最优,且跳出局部最优需要较多次迭代。说明FPA算法有时会陷入局部最优难以跳出。

图2 Sphere函数收敛曲线

图3 Rastrigin函数收敛曲线
为了解决FPA算法后期收敛速度较慢,容易陷入局部最优的问题,提出了基于天牛须搜索的花朵授粉算法。
3 基于天牛须搜索的花朵授粉算法
为了提高FPA算法的收敛速度,将BAS算法融入FPA算法的全局寻优部分。为了提高FPA跳出局部最优的能力,在局部寻优部分用新的差分策略代替原有策略,并加入小概率变异,从而实现BASFPA算法。具体实现如下:
(1)初始化算法参数。
(2)初始化种群,并计算所有解的适应度值。
(3)若 p>rand,使用天牛须优化的全局搜索对解进行更新。
(4)若 p (5)计算所有解的适应度值,更新全局最优解和全局最优解的适应度值。 (6)判断是否满足迭代结束条件,满足退出迭代,并输出最优解及其适应度值,不满足返回(3)。 BASFPA算法流程图如图4所示。 天牛须搜索(Beetle Antennae Search,BAS)是2017年提出的一种智能优化算法。类似于遗传算法、粒子群算法、蚁群算法等智能优化算法,BAS不需要知道函数的具体形式,就可以实现高效寻优。与其他群智能优化算法不同,BAS只需要一个个体,运算量大大降低。 天牛须搜索的仿生原理如下:当天牛觅食时,天牛不知道食物在哪里,根据食物气味的强弱来觅食。如果天牛左边触角收到的气味强度比右边大,那下一步天牛就往左飞,否则往右飞。食物的气味就相当于一个函数,天牛的目的是找到全局气味值最大的点。仿照天牛的行为,抽象出BAS算法: (1)天牛在三维空间运动,为了能在任意维函数使用天牛须搜索,将天牛的觅食行为推广至任意维空间。 (2)天牛抽象为一个质点,左右两须位于质点两边。 (3)天牛的步长与两须间的距离成固定比例。 (4)天牛前进一个步长后,头的朝向是随机的。 图4 BASFPA算法的流程 BAS算法流程描述如下: (1)对于k维优化问题,质心表示为x,左须xl,右须xr,两须距离d,其中x,xl,xr都是k维向量。 (2)由于天牛头的朝向随机,所以生成随机k维单位向量来表示天牛左须指向右须的向量: 其中,rands(k,1)表示生成k维的随机向量。 所以左须可以表示为: 右须为: 其中dt表示在第t次迭代时两须的距离,xt表示第t次迭代时天牛质心的位置。 (3)计算左右两须xl和 xr的适应度值 fl和 fr,根据 fl和 fr的大小关系,判断天牛的前进方向: 其中sign为符号函数,δt为第t次迭代时天牛的移动步长。 (4)计算天牛移动后的适应度值,并左右两须距离和步长: 其中,dt为第t次迭代时两须的距离,eta_d和eta_δ为两须距离和步长的衰减系数,通常取0.95。 (5)判断是否符合迭代结束条件,符合结束迭代,不符合重复(2)~(4)直到符合条件。 由文献[12]可知,BAS算法有很强的全局搜索能力,故将BAS算法应用于FPA算法的全局寻优部分,帮助FPA快速收敛。 在全局搜索部分,在花粉个体按照基本FPA算法移动后,将个体视为天牛,计算其按照BAS算法移动后的适应度值,并与移动前的适应度值比较,若移动后的适应度值更优,则进行移动,否则不进行移动。 改进后的全局搜索为: 由于FPA算法易陷入局部最优,故在其局部寻优部分加入扰动进化策略,以提高算法跳出局部最优的能力。 FPA算法在局部搜索的策略类似于差分进化算法的变异操作。花朵授粉算法的局部搜索策略为: Zheng[13]等对差分进化算法进行研究后,提出了一种新的差分策略: 式(13)中,以全局最优解作为基向量,个体本身参与变异,能够更好地平衡变异的随机性和确定性,既能加快收敛速度,又能减慢算法陷入局部最优的速度。 仅采用单一的差分策略仍有可能导致算法陷入局部最优,而是否能够跳出局部最优是算法解得全局最优的关键。为了增强算法跳出局部最优的能力,在新的差分策略的基础上,加入了小概率变异策略,使算法跳出局部最优: 最终的局部寻优表达式为: 其中,pl∈[0,1],一般选取为0.1。其中是解Xi迭代t次和t+1次后的值,为第t次迭代的全局最优解。 基本花朵授粉算法存在两层循环,其时间复杂度为O(n2)。在BASFPA中,没有添加新的循环,故算法的时间复杂度仍为O(n2)。由于全局寻优在默认转换概率0.8下只有20%的执行概率,且天牛须搜索仅需进行两次适应度值计算,故在全局寻优加入了天牛须搜索对算法的运行时间影响较小。而变异策略添加一个运行概率为10%的向量加法,对算法的运行时间几乎没有影响。 本文选择具有代表性的6个函数来验证BASFPA算法的有效性和优越性,包括单峰、多峰函数,并将测试结果与FPA算法,其他改进的FPA算法进行比较。测试函数选取CEC2013 benchmark[14]测试函数的一部分: 本文测试方案如下: (1)固定迭代次数下,测试FPA、MFPA、tFPA、BASFPA在30维下的寻优性能。 (2)固定迭代次数下,测试FPA、MFPA、tFPA、BASFPA在100维下的寻优性能。 (3)相同种群数,迭代次数下,对比BASFPA与萤火虫算法、布谷鸟算法的收敛精度。 (4)相同参数下,设置转化概率 p=0,比较FPA和BASFPA的全局寻优性能。 (5)相同参数下,设置转化概率 p=1,比较FPA和BASFPA的局部寻优性能。 本实验下,各算法种群数为20,迭代次数1 500次,函数维度均为30维,BASFPA的d0=1,δ0=2,eta_d和eta_δ均为0.95。每种算法独立运行50次,统计各算法的最优值、平均值、最差值和寻优成功率。实验结果如表1所示。 表1 低维下的性能分析 从表1可以看出,BASFPA算法的最优值、平均值、最差值均优于FPA、tFPA和MFPA算法。BASFPA算法相比FPA算法,在各函数下寻优结果均有7~20个数量级的提升。除F5的寻优成功率为90%外,其他函数的寻优成功率均为100%。 为了更直观地比较BASFPA算法与其他三种算法寻优能力,将各算法的收敛曲线表示为图5~图10。可以看出,在F1~F6寻优中,BASFPA算法能够快速收敛,并且只有在F6函数寻优时陷入局部最优,但很快跳出,说明在局部寻优引入新的变异策略能够帮助算法跳出局部最优。 图5 F1收敛曲线 图6 F2收敛曲线 图7 F3收敛曲线 图8 F4收敛曲线 图9 F5收敛曲线 图10 F6收敛曲线 为了检验BASFPA达到固定精度所需的迭代次数,设置实验如下: 各算法种群数为20,函数维度均为30维,BASFPA的d0=1,δ0=2,eta_d和eta_δ均为0.95。每种算法独立运行50次,目标收敛精度为10-3,统计各算法达到收敛精度所需的迭代次数,如果在3 000次迭代后仍未达到目标精度,则认为寻优失败。实验结果如表2所示。 从表2可以看出,对于6个测试函数,BASFPA算法无论是最小收敛代数还是平均收敛代数均优于原算法,与其他花朵授粉改进算法相比,迭代次数明显降低。由此可见BAS算法对FPA算法的改进是有效的。 为了比较BASFPA和其他优化算法的寻优精度,设置实验如下: 各算法种群为20,迭代次数为1 500次。萤火虫算法[14](Firefly Algorithm,FA)的参数为α=0.2,β=0.7,γ=2;布谷鸟算法[15](Cuckoo Search,CS)的参数为:pc=0.1,p=0.25。BASFPA的参数同4.2节,每个算法在每个函数独立运行50次。实验结果如表3所示。 从表3可以看出,对于6个测试函数,BASFPA算法无论是最小收敛代数还是平均收敛代数均优于FA和CS算法,在F2、F3的寻优中,只有BASFPA能收敛到目标精度。 表2 BASFPA在固定收敛精度的实验结果 表3 低维下的性能分析 为了检验天牛须搜索对FPA的改进是否有效,将算法的转换概率p设置为0,即全部进行全局寻优。设置实验条件同4.2节。 从表4可以看出,BASFPA在只进行全局寻优时,寻优的效果均好于FPA算法,说明在排除了局部寻优的影响下,天牛须搜索对全局寻优的改进是有效的。 表4 天牛须搜索有效性检验 为了验证局部搜索中添加变异机制对FPA的改进是否有效,将算法的转换概率 p设置为1,即全部进行局部寻优。设置实验条件同4.2节。实验结果见表5。 表5 变异机制有效性检验 从表5可以看出,BASFPA在只进行局部寻优时,寻优的效果远好于FPA算法,说明新的差分策略有助于算法寻优,且小概率变异没有导致寻优信息丢失。 花朵授粉算法作为新型群智能算法,存在收敛速度慢、寻优精度低的缺点。针对这些不足,本文通过引入天牛须搜索算法改进原花朵授粉算法,提出了BASFPA算法。通过实验对比,BASFPA算法在低维下和高维下的寻优精度较原FPA算法均有较大提升。3.1 天牛须搜索介绍




3.2 基于天牛须搜索的全局寻优

3.3 变异策略




3.4 算法时间复杂度分析
4 仿真实验及结果分析
4.1 测试方案
4.2 低维下的性能分析




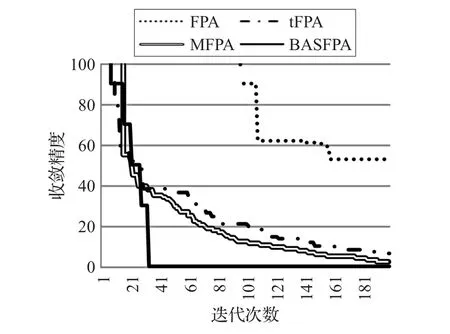
4.3 固定精度下性能分析
4.4 BASFPA与其他优化算法对比


4.5 天牛须搜索有效性检验

4.6 变异机制有效性检验

5 结束语

