高考数学试题与课程标准一致性研究——以2017年“全国Ⅰ卷（理科）”为例

陈鹃娟，刘婉悦，方朝玲

（广西师范大学数学与统计学院，广西桂林541004）

21世纪初，在Applied Measurement in Education上介绍一系列的一致性研究成果，引起国际对学业评价与课程标准一致性研究的重视。Achieve一致性分析模式在国外数学教育领域得到广泛应用，国内也有不少学者聚焦Achieve一致性分析评介[1]。全国Ⅰ卷高考数学试题由国家教育部门统一命制，影响范围较大，因此本文采用罗斯曼（R.Rothman）等人开发的Achieve一致性分析模式，对2017年全国Ⅰ卷高考数学试题与课程标准一致性进行研究，以期为我国数学考试命题和教育教学提供启示。

一、研究对象

本文选取2017年全国Ⅰ卷高考数学试题与《高中数学课程标准（实验）》进行一致性研究。

二、研究工具

课程标准包含不同知识领域，各知识领域由若干学习目标组成。Achieve一致性分析模式从六项指标分析试题与课程标准的一致性，分析指标含义以及评价标准如下。

（一）内容向心性

内容向心性分析试题考查学习目标的“内容要求”与课程标准的学习目标是否一致，分为3个等级：“2”表示完全一致，“1”表示部分一致，“0”表示完全不一致，如表1。

（二）表现向心性

表现向心性分析试题考查学习目标的“认知要求”与课程标准的学习目标是否一致，分为3个等级：“2”表示完全一致，“1”表示部分一致，“0”表示完全不一致，如表1。

（三）难度来源

难度来源分析试题能否科学地评价学生对学习目标的掌握，分为2个等级：“1”表示挑战来源恰当，“0”表示挑战来源不恰当（如题干描述或图表出现错误），如表1。

（四）难度水平

难度水平分析各知识领域试题难度的“覆盖”情况，若各知识领域试题分布的难度水平越广，则对应知识领域的试题难度水平越合适。结合《高中数学课程标准（实验）》，将难度水平分为4个等级：了解、理解、掌握和灵活运用，如表2。

（五）平衡性

平衡性分析试卷考查的知识领域与课程标准的接近程度，若试卷涉及知识领域个数与课程标准越接近，平衡性一致性程度越高，如表2[2]。

（六）范围性

范围性分析试题各知识领域考查课程标准学习目标的比例。各知识领域中，试题考查的学习目标数目与课程标准学习目标数目之比为比值2，若该比值于50%至66%，范围达到可接受程度，大于67%，范围达到满意程度，如表2。

三、研究过程

第一阶段：首先结合高中数学课程标准，分析试题描述和解题过程，剖析试题涉及的学习目标，其次匹配试题所属主要知识领域，进而理清试题“内容向心性”“表现向心性”以及“难度来源”等级，对数据进行标准化处理，如表1。

第二阶段：如表2，首先加和课程标准中各知识领域学习目标数目；其次，计算试卷考查学习目标数目与课程标准中各知识领域学习目标数目之比，为“范围”指标比值2，分析试题主要匹配的知识领域，得到各知识领域试题数目，即“平衡”指标。最后，判断各知识领域试题分别所处的难度水平。

四、研究结论

（一）内容向心性、表现向心性和难度来源等级一致性分析

如表1，内容向心性方面，全国Ⅰ卷“完全一致”比值为0.8667，表现向心性方面，“完全一致”比值为0.7000，表明试题考查学习目标的内容要求和认知要求试卷与课程标准具有较好一致性。难度来源方面，“完全一致”达100%，表明试题无科学性错误。

（二）范围、平衡和难度水平数据分析

如表2，范围方面，算法初步与解三角与三角函数比值2均达到50%，为可接受程度，数列比值2大于67%，达到满意程度，即仅有3项知识领域符合范围评价标准。平衡方面，各个知识领域均有试题分布，即平衡性一致性程度较高。难度水平方面，统计与概率分布于4个难度水平，即统计与概率知识领域难度水平分布较好。

综合分析表明，全国Ⅰ卷高考数学考查学习目标的内容要求和认知要求与课程标准具有较好一致性，各个知识领域试题设置全面，试题无科学性错误，试卷分别在内容向心性、表现向心性、平衡和难度来源一致性较好。但试卷各知识领域考查课程标准的学习目标大于50%的比值总体较少，即范围指标一致性程度较低；各知识领域试题覆盖的难度水平相对集中，表明难度水平指标一致性较低，究其原因与全国Ⅰ卷高考数学试题的知识领域有所侧重和评价方式有关。

五、启示

高考和课程标准长期不一致易造成教学实施、评价以及数学核心素养培养产生偏离。综合上述研究可得出如下启示：第一，优化课程标准的学习目标。张奠宙在接受访谈时认为中学数学注重于理解数学，建议减掉一些可用可不用的内容，如线性规划作为优化理论，普遍适用性不强；又如，推理与证明作为高层次的数学认知活动之一，融入具体知识领域有益命题者准确把握学习目标要求，也利于范围指标一致性的提高。第二，适当改革高考选拔模式。尽管部分地区已实行自主命题考试，但模式化痕迹明显，对课程标准要求的“情感与态度”“过程与方法”考查存在一些局限。因此可借鉴已受到了国际数学教育的认可PISA和ALEVEL等考试形式，以提高数学试题与课程标准的一致性。

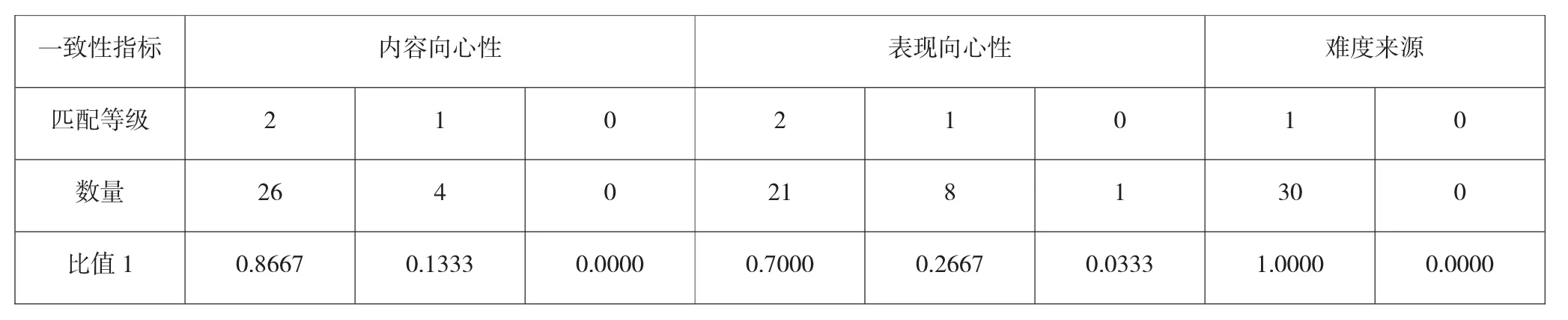
表1 内容、表现向心性以及难度来源等级统计表

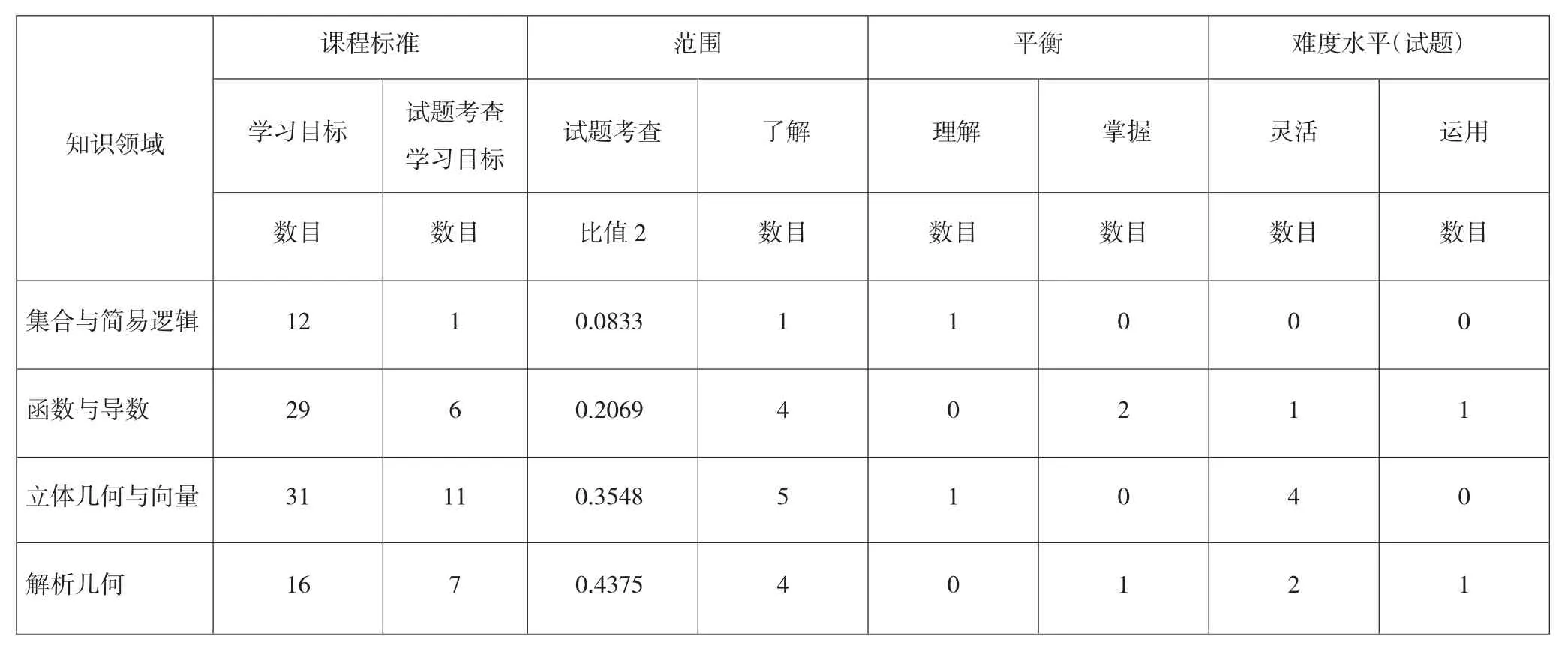
表2 －1 范围、平衡以及难度水平统计表

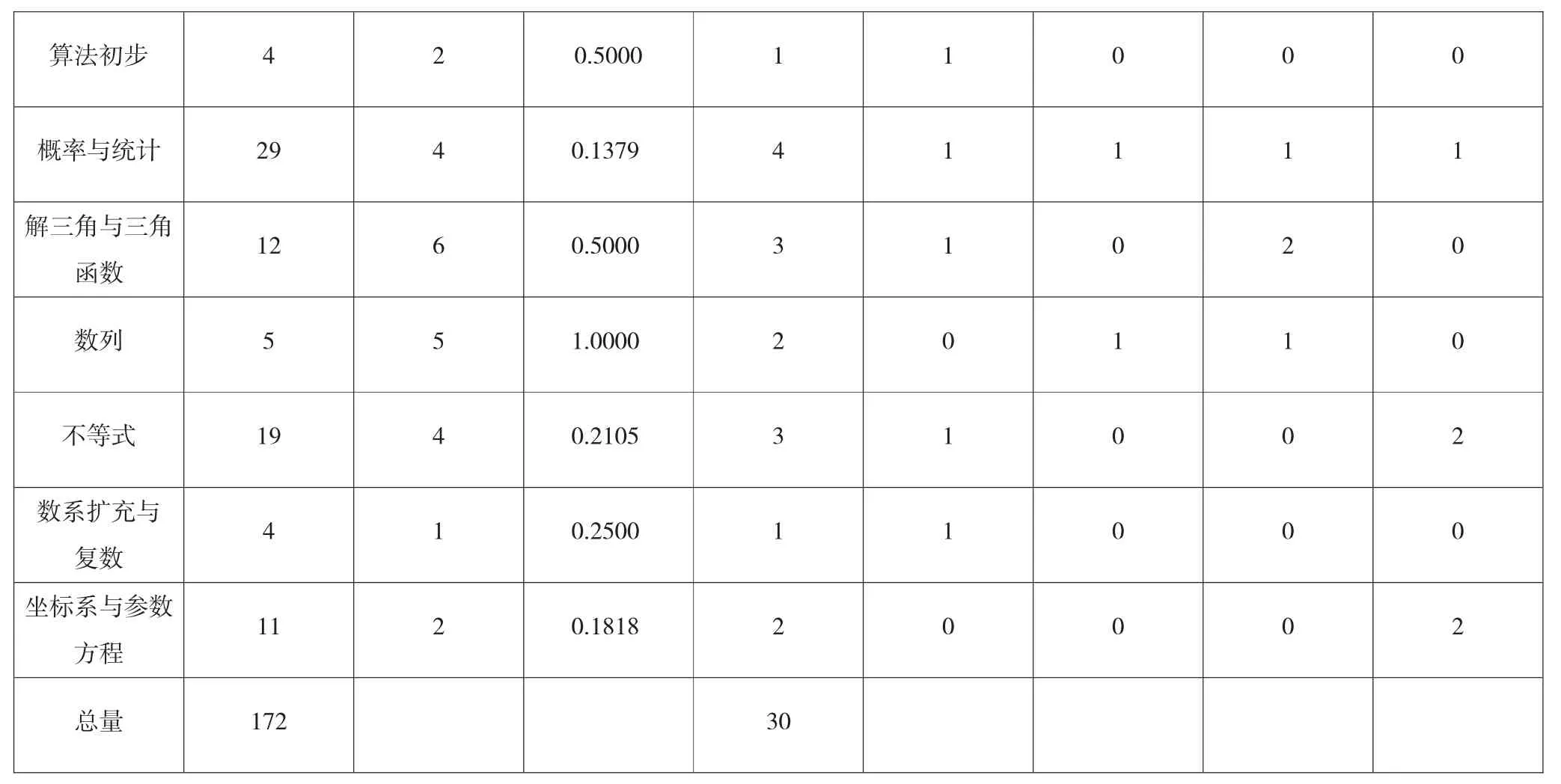
表2 －2 范围、平衡以及难度水平统计表