结合自组织映射网络及三角形算法的星图识别方法
,,,,,,
1.中国科学院 上海技术物理研究所 中国科学院红外探测与成像技术重点试验室,上海200083 2.中国科学院大学,北京100049
飞行器的导航技术是飞行器进行太空探索的关键技术之一,而飞行器姿态的解算是导航技术的基础。依据不同的参考系,可制作不同的姿态敏感器,如地球敏感器、太阳敏感器及恒星敏感器(简称星敏)等。相对于其他光电姿态敏感设备,恒星敏感器具有测量精度高、抗干扰能力强、能实现自主导航等优点,目前已成为卫星等航天器上最主要的姿态测量仪器。
恒星敏感器的关键技术主要包括:星点质心提取、星图识别和姿态解算,其中星图识别过程决定着恒星敏感器的姿态识别率、姿态输出速度。目前,国内外提出了很多星图识别方法[1],文献[2]将其分为3大类:基于星座特征的方法、基于字符模式的方法、基于智能行为的方法。其中,基于星座特征的三角形算法是最经典且应用最广的算法,该方法简单易懂,易于实现,但是存在识别速度慢、易出现冗余匹配等问题。国内外不少学者从各方面对三角形方法进行了改进,例如优化搜索方法[3-4]、采用不同的天区分割方法[5]、构建不同的特征量[6-10],这些方法都一定程度上提高了搜索的速度,减少了匹配冗余。此外,基于星座特征的方法还包括主星识别算法[11-12]及匹配组算法[13-14]。基于字符模式的算法主要指栅格算法,该算法由Padgett提出[15],具有识别速度快、存储量小的优点,但当干扰较大时,识别率会迅速下降,且要求观测星不可少于6个,为了提高网格算法的识别率,先后出现了弹性灰度网格算法[16]、圆形栅格算法[17]、扩充栅格法[18]、KMP星图识别算法[19]。基于智能行为的方法是随着人工智能的发展而提出的,主要包括基于遗传算法的识别方法和基于神经网络的识别方法。其中,神经网络技术最早于1989年被Alveda提出应用到识别算法中[20],随后Hong提出了基于模糊神经网络的星图识别方法[21],国内学者也做了相应的研究[22-23],已有的基于神经网络的算法在训练结束后可以实现快速识别,但是实现较困难,存在一定的误识别。
本文将神经网络技术中的自组织映射网络(Self-Organizing Map, SOM)应用在星图识别当中,首先根据观测星的分布特点实现SOM网络的模糊识别,确定与观测星相似的恒星,缩小三角形的搜索范围,再利用三角形算法查找到匹配的三角形,验证后计算得到姿态信息。该方法结合了SOM网络优秀的分类能力以及三角形算法可靠的角距匹配能力,缩小三角形的搜索范围实现快速匹配的同时,提高了系统的抗干扰性和可靠性。本文以全天星图识别为研究目标,实现了新算法的仿真测试,并基于实验结果进行了比较和探讨。
1 导航星的选取
星图识别的实质就是从星表中找到与观测星所匹配的导航星,作为星图识别的唯一判断依据,导航星的选取至关重要。既要保证星表的完备性,又要适当删减星表中多余的导航星,减少星表数据存储量,提高数据利用率[24]。基于系统的成像性能及识别算法的特点,筛选并组建出适合识别系统的导航星星库。
1.1 挑选基本星表
本文用于仿真的星敏感器的性能是:方视场15°×15°,星等的灵敏度可达6.0视星等。选用2007年发表的第二版《依巴谷星表》作为基本星表,该星表中恒星的位置精度高达千分之一角秒,满足精度需求。选出依巴谷星表中星等小于6.0且有确定赤经和赤纬的恒星,共5041颗,由于这其中包含了星等值不确定的“变星”和两星之间角距太小的“双星”,需要对星表进行进一步的处理。
1.2 选择性删除变星
对于星表中的变星,进行有选择性的删除,由于部分变星在亮度变换范围内均能成像,部分变星的变化范围超出了可观测的最高星等,所以保留星等最大值小于6.0的变星,删除星等最小值小于6.0且最大值大于6.0的恒星,总共删除62颗变星。
1.3 合并双星
由于恒星的成像会经过弥散处理扩散到多个像元,当两颗星之间的角距很小时会使两颗星的成像像素重叠,从而干扰单星的提取精度,甚至将两颗星误判为一颗星。在很多星表的预处理过程中,采用了删除两颗星或者两颗中较暗星的方式,这样处理比较简单,但是当视场中恒星数量不多时,会影响系统的识别率。本文采用合并双星的方法,根据所仿真的恒星敏感器的性能指标,选择将角距小于0.059°(4个像元尺寸大小)的双星合并,得到一颗拥有新的星等、赤经和赤纬的恒星,删除星表中构成双星的两颗星,加入合并生成的星。设两颗星的星等分别为m1、m2,亮度分别为d1、d2,方向矢量分别为v1、v2,两颗星之间的角距为p;合并的新星的星等、亮度、方向矢量分别为m、d、v,与原两颗星之间的角距分别为p1、p2,当用光流密度来表示星的亮度时[25],两颗星的亮度比
d1/d2=e(m2-m1)/2.5
(1)
合并得到星的亮度可以看成是两颗星的亮度的合成,于是有
d=d1+d2
(2)
通过推导,得到合并后新星的星等
m=m2-2.5ln[1+e(m2-m1)/2.5]
(3)
又由于角距与亮度存在关系式
d1p1=d2p2
(4)
得到
p=p1+p2=p1[1+e(m2-m1)/2.5]
(5)
根据方向矢量与角距的关系式
vsinp=v1sinp1+v2sinp2≈v1p1+v2p2
(6)
从而得到合并后新星的方向矢量v为
v=(v1p1+v2p2)/sinp
(7)
根据坐标转换公式,得到新的赤经赤纬。
试验中发现,星表中存在3颗星之间的角距均小于0.059°,在这种情况下,将其中两颗星合并之后再与第三颗星合并,最终形成一颗新的星,将其替换原有的三颗星。双星处理过程挑选出了27对双星,实际删除51颗,加入25颗合并后的星。经过变星及双星处理,星表最后剩下4953颗恒星。
2 结合SOM网络及三角形算法的星图识别方法
2.1 识别系统原理
本文提出了一种结合神经网络技术及三角形算法的星图识别方法,恒星敏感器工作期间,在没有先验姿态的情况下,可以采用该方法进行全天星图识别。如图1所示,该识别系统主要包括两部分:星表的预处理分类、实测星图的识别。
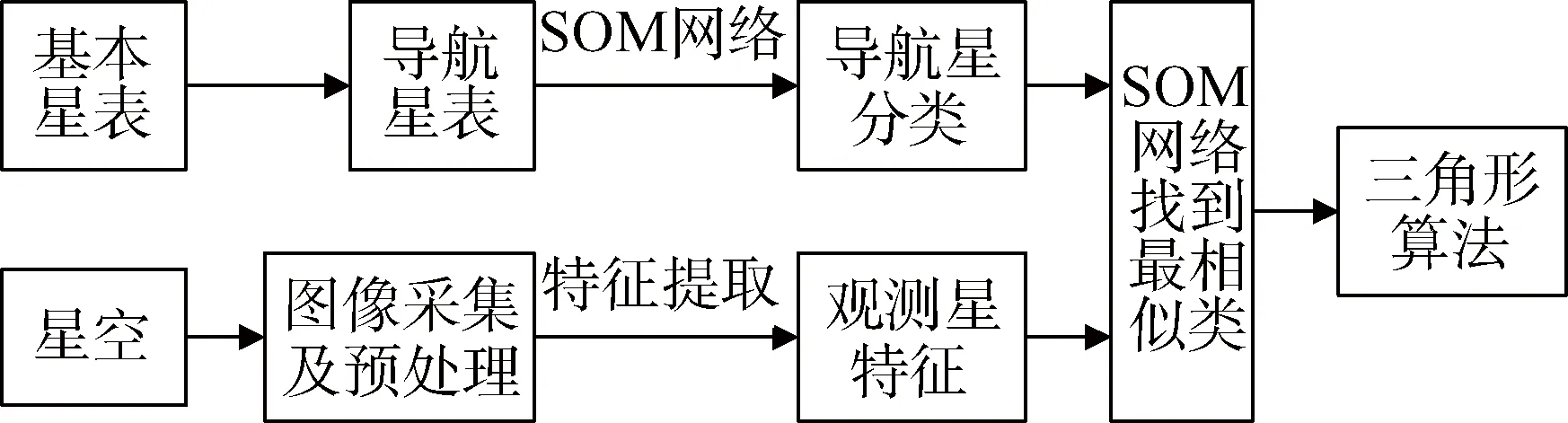
图1 识别系统的原理Fig.1 Schematic diagram of recognition system
预处理分类过程中,基于筛选好的星库,根据每颗星的邻近星的分布特点,构造特征向量,采用神经网络技术构建分类网络,将星表中所有恒星分成多类,并将每颗恒星与其邻近星的组合三角形信息存储在对应的三角形库中。
星图识别过程中,用同样的方法生成待识别星的特征向量,通过分类网络输出最相似类,在该类对应的三角形库中应用三角形算法,找到匹配三角形。当验证成功之后,计算并输出该识别姿态。
2.2 SOM网络
自组织特征映射网络又称为自组织映射网络(SOM),最早由神经网络专家Kohonen于1981年提出。它模拟了大脑中不同区域的神经网络细胞分工不同的特点,通过网络的学习,使不同区域有不同的响应特征[26]。自组织映射算法是无监督学习算法的一种,网络的分类由多个输入神经元共同协作完成。SOM网络输出层引入了拓扑结构,每个神经元附近的神经元会得到更新,使相邻神经元变得更相似,以更好地模拟生物学中的侧抑制现象,具有聚类和高维可视化的特点。
2.3 星表的预分类处理
利用自组织映射对恒星进行分类,需要构建有效的特征向量代表恒星,作为网络的输入。如图2所示,采用径向特征[25]来构造星的特征向量:以星表中每颗恒星为圆心,以固定的角距增量画同心圆,将每颗星周围的圆区域均分成N等分,根据区间内恒星的统计量构造N维的特征向量,与图2所对应的10维特征向量为[0,0,1,2,1,2,1,2,0,1]。
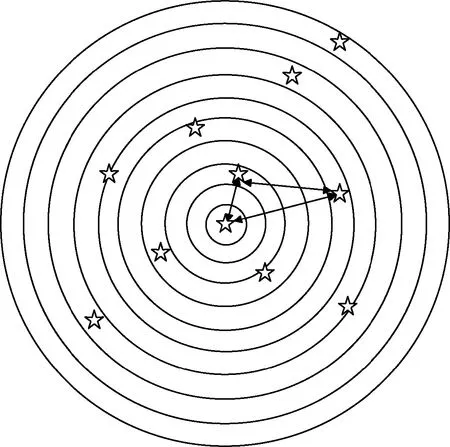
图2 特征向量的构造方法Fig.2 Method of constructing feature vector
利用自组织映射网络对4953颗恒星进行分类,将N维特征向量作为网络输入,如果选择分成81类,训练网络的迭代次数设为700,则网络将循环输入4953颗星700次,训练结束时,恒星被较均匀的分在81类中,如图3所示,数值代表每一类的恒星统计量。

图3 分类结果Fig.3 Result of the classification
表1列出了该分类结果下第1类别中部分恒星的特征向量,从表中可以看到,这些特征向量具有相似的数字变化规律,前几列偏小,而第7列和第9列的数值较大,即网络把具有相似特点的特征向量的恒星视为了一类。该方法所构造的特征向量反映了恒星周围区域内星的分布特点,能有效的将具有相似邻近星分布的星归为一类。又由于特征向量的构造对恒星的位置误差有一定的容忍性,使得该分类方法具有较好的鲁棒性,当星点引入了位置误差或者周围星的数量发生变化时,网络依然可以输出其最相似类。
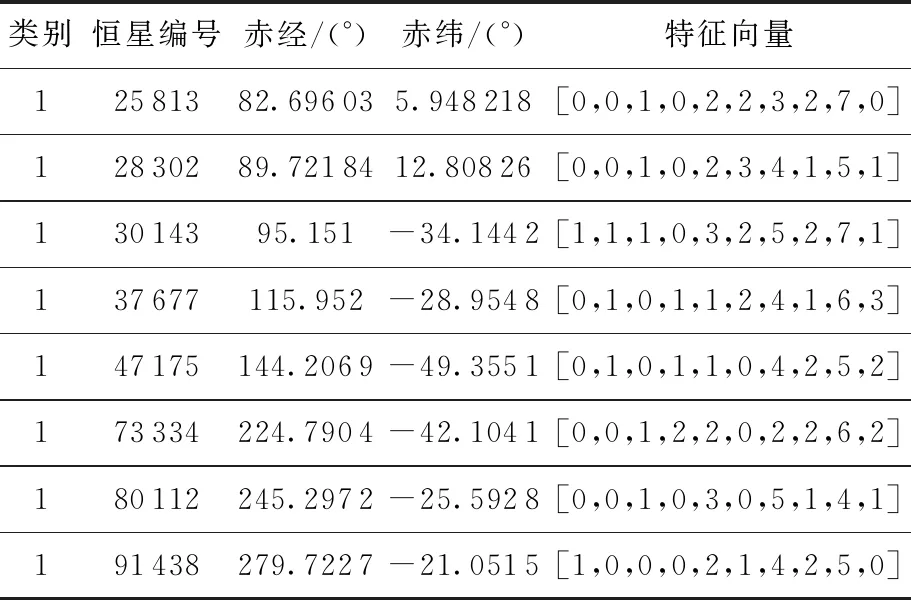
表1 第1类中部分信息
构建恒星特征向量的同时,在其邻近星中挑选出最亮的或者最近的几颗星,与该星组成多个三角形,将三颗星及三个角距值作为该三角形的信息,存储到网络识别类所对应的三角形库中,形成81个三角形信息库。
2.4 结合SOM网络及三角形算法进行识别
基于已建好的星表和已训练好的SOM网络,星图识别过程的步骤如图4所示。
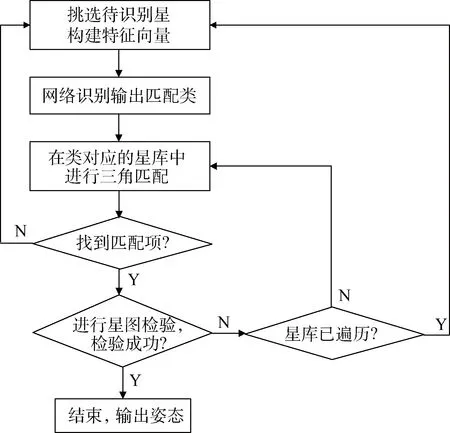
图4 星图识别的算法流程Fig.4 Flowchart of star pattern recognition algorithm
1)输入待识别星,采用相同的特征提取方法,生成待识别星的特征向量并输入已训练好的自组织映射网络,网络输出该星与所有类的相关度,选择相关度最高的一类代表该星进行后面的识别匹配。
2)将待识别星与其邻近区域内最亮或者最近的M颗星进行组合,生成M×(M-1)/2个三角形,按照星的亮度或者距离对三角形进行排序。
3)根据待识别星所属的种类,在该类所对应的三角形库中,应用三角形算法,依次匹配排好序的组合三角形。
4)当找到匹配三角形时,根据待识别星所匹配的恒星在星表中的信息,以及待识别星在实测星图中坐标,生成星表中该星可形成的理论星图,验证理论星图与实测星图的差距,如果理论星图中的恒星大部分都能在实测星图中找到,且坐标误差在允许的范围内,则认为识别成功,若验证不通过则继续搜索匹配。
5)当搜索完待识别星的所有组合三角形,却依然无法找到验证成功的三角形时,则放弃该星的识别,回到1),选择实测星图中下一颗星进行识别。
6)若识别成功,则根据QUEST方法的姿态解算公式,计算出实测星图所对应的姿态。
3 星图模拟
3.1 星等到灰度的变换
为了验证算法的可行性和性能,采用模拟星图来进行试验。随机生成视轴指向,根据星表中恒星的赤经和赤纬,通过坐标变换,将视场中的恒星投影到15°×15°的成像平面上。不同星等之间的亮度呈现关系是:星等值每降低1,亮度变为前一星等的2.512倍。由于电脑仿真灰度值范围有限仅为0~255,而81%的恒星星等值在4.5~6之间,为了尽可能呈现出更多恒星的亮度变化,将星等值为4.5的恒星灰度值设为255,6等星的灰度值则为64,进行星等和灰度值之间的转化:
(8)
式中:m为恒星的星等值;g为灰度值。又考虑到试验时恒星成像并没有在像元正中心,像素灰度值一般小于g,为了更加突出暗星,进行相应的修改。由于67%的恒星星等值在5~6之间,将星等值为5的恒星灰度值设为255,6等星的灰度值则变为101.5,进行星等和灰度值之间的转化:
(9)
3.2 点扩散
为了提高恒星的定位精度,实测星图中星点并不是集中在一个像元内,而是被散焦到多个像元上,模拟该过程,将星点进行高斯点扩散,使之扩散到3×3的像元上,形成模拟星图。星点图像用高斯函数近似表示:
(10)
式中:g由式(9)得到;gi为像素i的灰度值;σ为光斑弥散半径,取值为0.45;Δx为像素i中心点的横坐标与星点横坐标的差;Δy为像素i中心点的纵坐标与星点纵坐标的差。当m<5使g>255时,仍将该值代入式(10)中得到gi,当gi>255时,电脑将其视为255进行显示。
3.2 噪声模拟
星图成像噪声主要有两方面[27]:一是器件在受到空间辐射时的散粒噪声和器件本身的转移噪声、输出噪声、暗电流噪声等,其中,暗电流噪声和散粒噪声相对来说影响较大;二是星空背景噪声,包括杂散光、宇宙辐射、星云等。将背景噪声看成10等星的亮度,即在原星图上加上灰度值255/2.51210-5,用高斯白噪声来代表器件的暗电流和散粒噪声。基于此星图进行仿真试验,图5为某视轴下模拟星图的局部示意。

图5 模拟星图的局部示意Fig.5 Diagram of local simulated star map
4 算法的仿真结果
4.1 参数选择对算法的影响
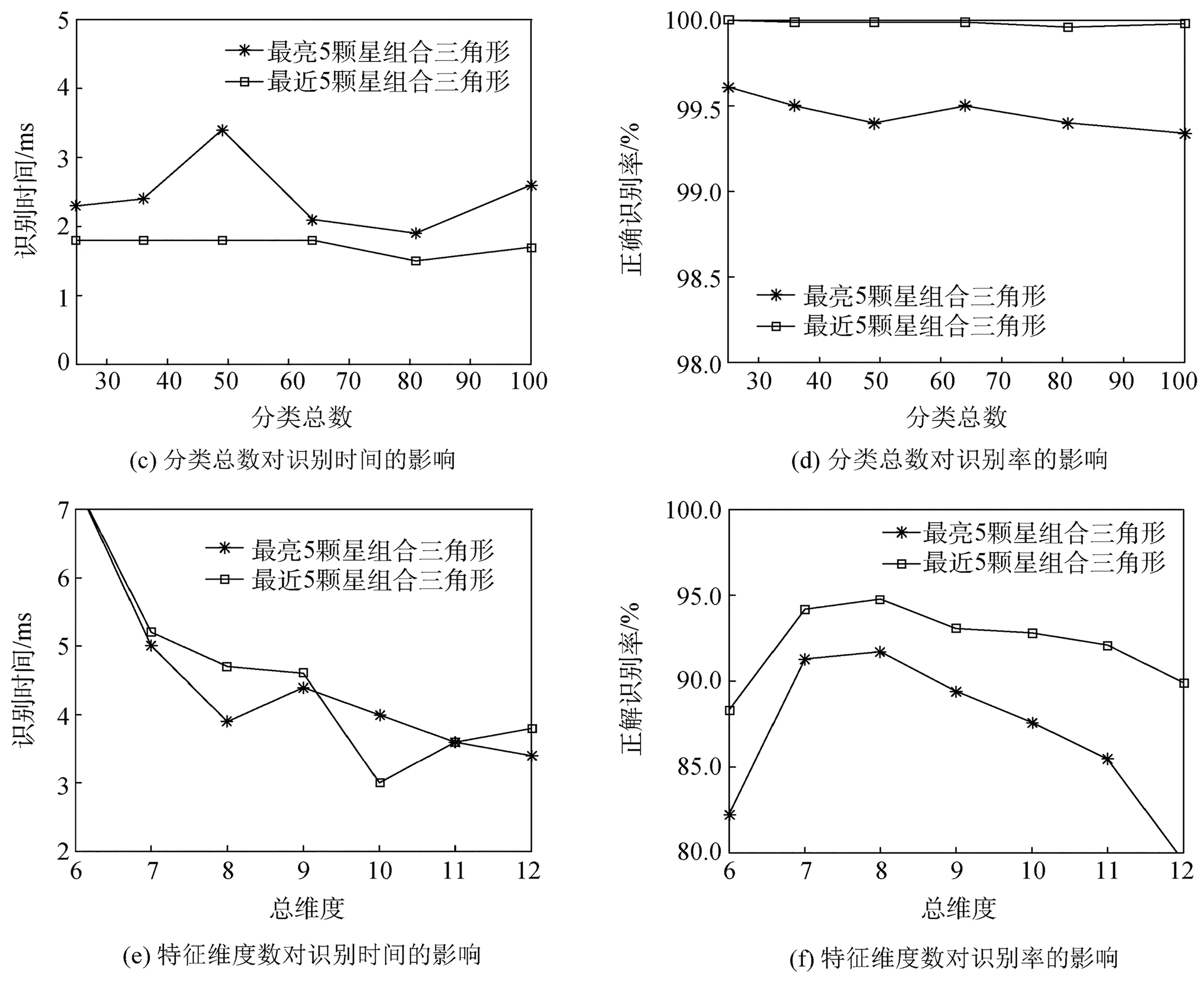
本文对于组合三角形的方法有两种,一是选择恒星周围最亮的5颗星进行组合,二是选择恒星周围最近的5颗星进行组合,通过一系列的仿真比较了这两种方法。其中,最亮或最近5颗星的选取范围与最大同心圆的选取范围一致,即在参与构建特征向量的周围星中选取,当参与的周围星不足5颗时,在该范围内选取所有周围星完成组合。探讨实验参数对识别效果的影响:更改训练时的迭代次数、分类总数、特征向量维度,分别比较两种三角形组合方法的识别效果。以下仿真试验的模拟噪声均选用均值为0.1的高斯白噪声,同心圆角距差设为0.5°,每次试验随机生成10 000个视轴下的模拟星图进行识别。图6(a)、6(b)的分类总数为81,特征维度为10,噪声为标准差0.017。图6(c)、6(d)的迭代次数为500,特征维度为10,噪声为标准差0.017。图6(e)、6(f)的分类总数为81,迭代次数为500,同心圆角距差为0.5°,噪声为标准差0.035。
如图6(a)、6(b)所示,当SOM网络的训练迭代次数为200时即可达到很好的识别效果,增加训练的迭代次数,识别效果变化不大。从图6(c)、6(d)得到,分类总数对识别效果的影响较小,综合识别时间及识别率的结果,当分类总数为60~80时,整体效果较好。图6(e)、6(f)反映了特征维度的选择对识别效果的影响,由于在标准差为0.017的噪声下,系统识别率很高,特征维度对其影响不明显,故增大了噪声的干扰,选择标准差为0.035的高斯白噪声进行实验。当保持同心圆的角距差0.5不变时,改变特征维度的同时也改变了恒星周围星的选取范围。当特征维度较小时,由于恒星周围参与统计的邻近星较少,特征向量包含的信息量不足以将恒星较好的分类,使得识别率降低;当维度较大时,若恒星离视场中央较远,同心圆所包含的区域将不能在图像上完整成像,导致统计量出现偏差,识别率降低。因此,对于15°×15°视场、6.0星等的星敏感器,可以选择分类数为60~80,基于固定的角距差0.5°,适合构造7~10维的特征向量。
从以上试验还可以看到,选取恒星邻近5颗星组合三角形的识别率更高,识别时间更短。当选择恒星邻近最亮5颗星组合三角形时,由于6等星星库中67%的恒星星等在5~6之间,所以当引入噪声时,导致星等误差较大,干扰了邻近星的亮度排序,会得到错误的5颗亮星。
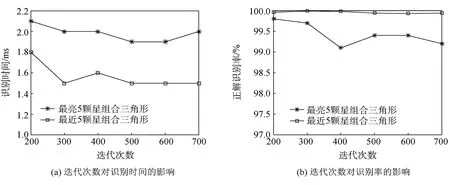
图6 不同参数下的识别效果Fig.6 Recognition under different parameters
续图6Fig.6 Continued
4.2 算法的抗噪性能
为了评估该星图识别算法对噪声的容忍性,由此来检测识别系统的健壮性,改变高斯白噪声的标准差,得到不同噪声干扰下算法的识别效果。
观察图7不同噪声下的识别效果,当系统噪声增加时,系统识别率降低,识别时间变长,计算所得的视轴误差增加,相比之下,邻近5颗星的组合三角形对噪声的容忍性更高。但是不论是哪一种方法,识别时间都低于5 ms,识别率在噪声标准差为0.025时仍高达99%,该噪声相当于在原星图上随机加上-10~60的灰度值。采用QUSET方法计算姿态,得到视轴误差在角秒级。
4.3 对星等不确定性的容忍度
在星敏实际应用过程中,探测器的灵敏度会产生波动,实际观测的最大星等值不一定严格地保持原设计值,如表2所示,改变星表的最大星等值,列出了对应的恒星总数,并将其与原设计星表进行对比,由于原设计星表65%恒星星等值在5~6之间,当最大星等值在6附近发生较小改变时,星表恒星数量即发生很大的变化。
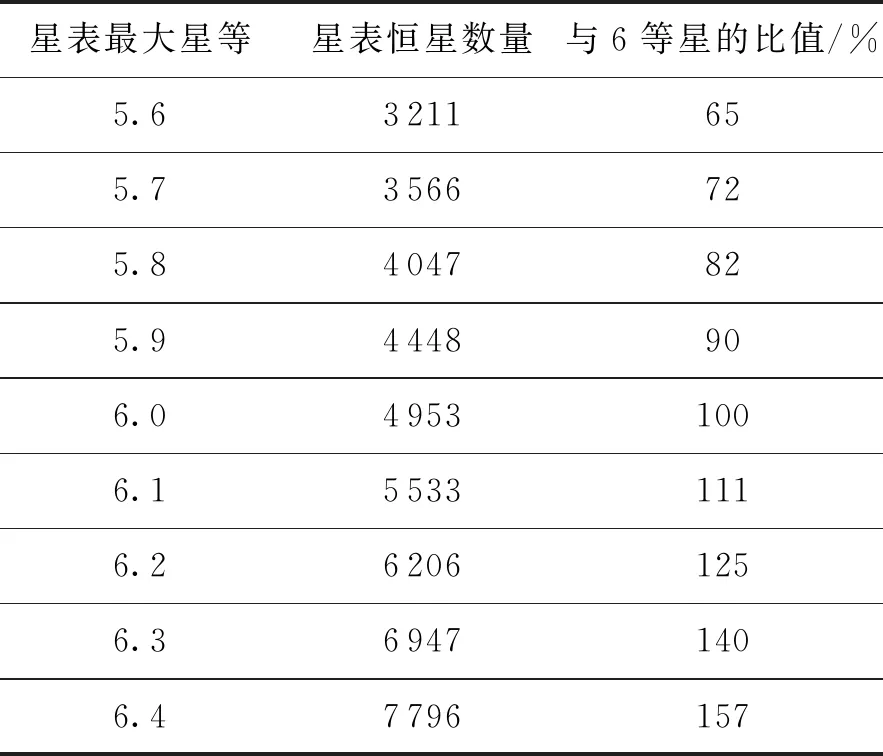
表2 不同星表的恒星数量
本算法的预分类识别对恒星分布的依赖性较强,为了评估算法的适用性,在保持匹配星表最大星等为6的情况下,改变仿真星表的最大星等值,即模拟探测器的灵敏度发生波动的情况。
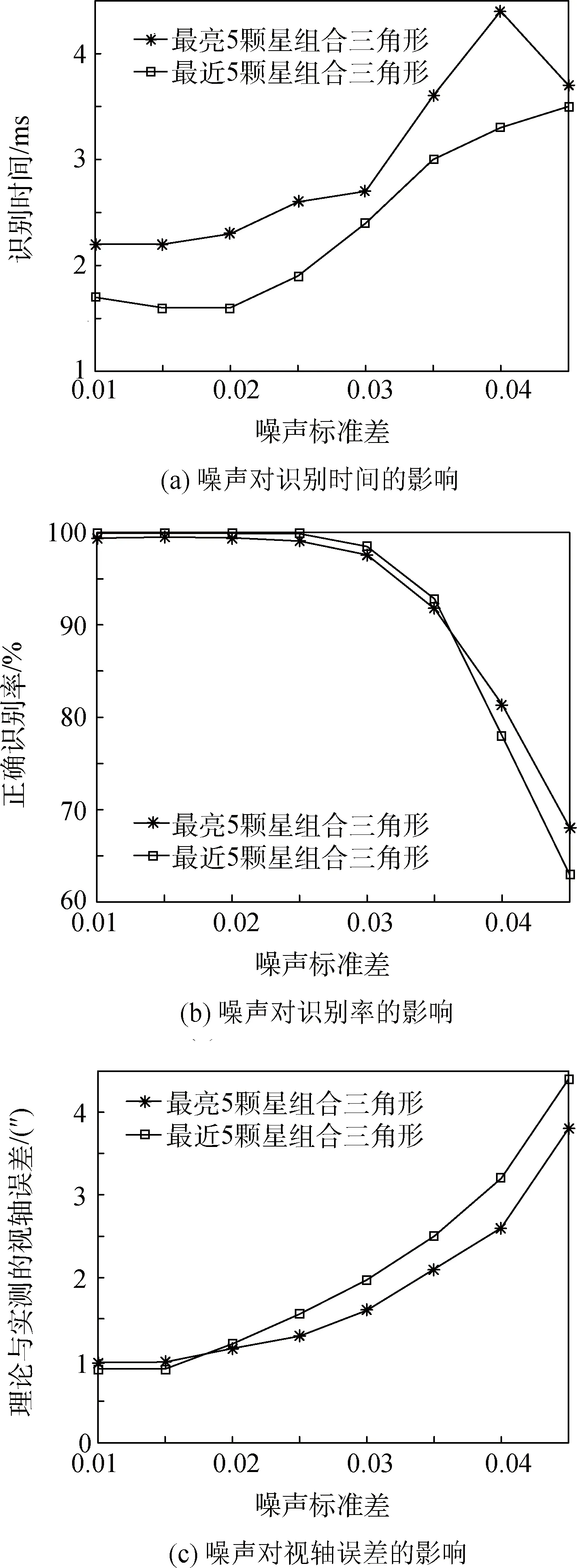
图7 不同噪声下的识别效果Fig.7 Recognition under different noise
如图8所示,保持原设计星表不变的情况下进行预分类、建立三角形库,改变仿真图像所用到的星表最大星等值,并随机生成视轴指向进行星图模拟,可以看到,增大最大星等值的改变量时,算法的识别率随之下降,而识别时间也随之增加。
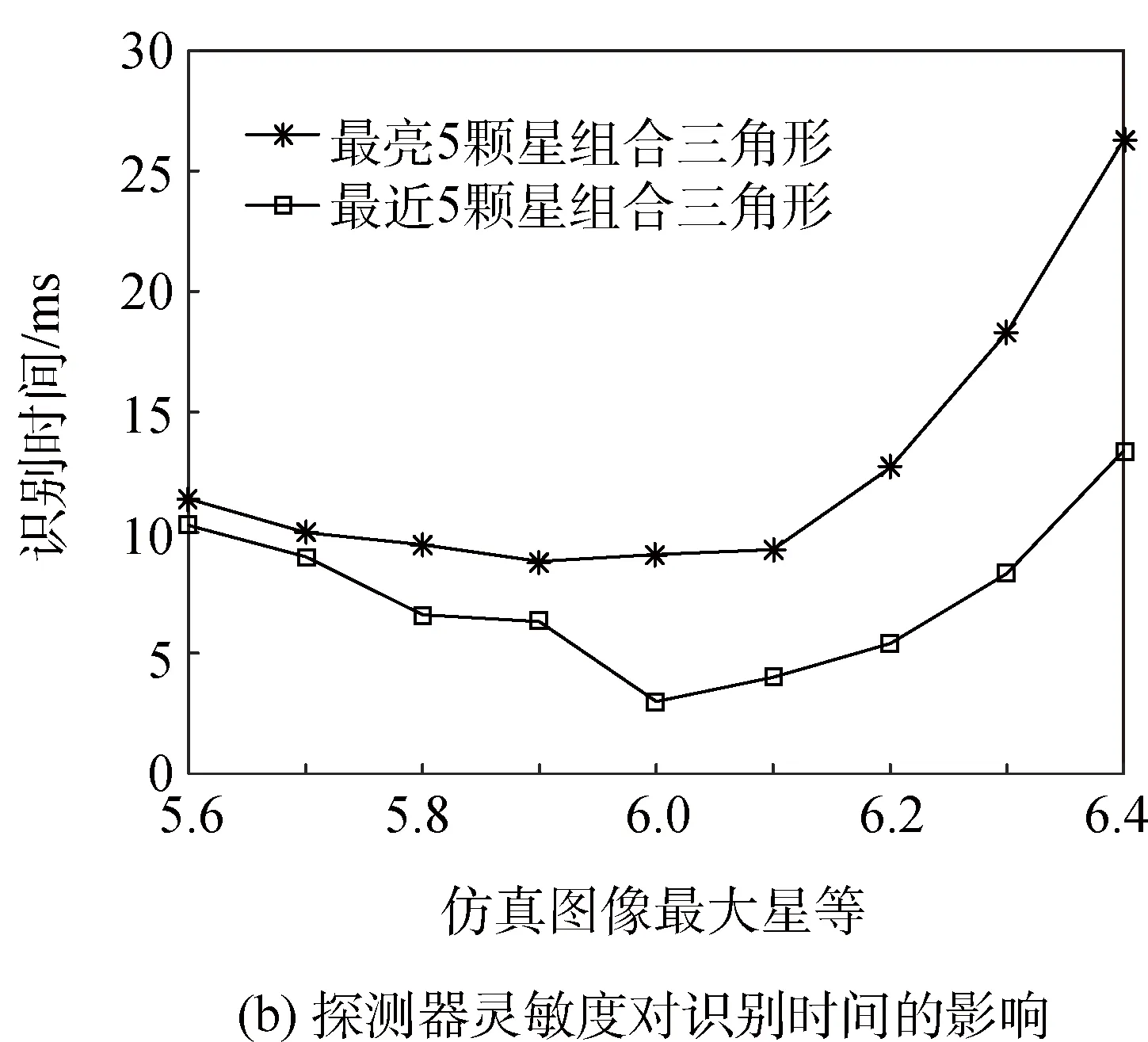
为了改善因为探测器灵敏度改变所造成的算法识别率的下降,将原算法中“在最相似一类中进行三角形匹配”改进为“在最相似五类中进行三角形匹配”,即扩大了三角形的搜索范围,同时也增加了对星等分布不确定性的容忍度。如图9为改进算法后相应的识别率及识别时间。
从图9可以看到,在将匹配范围扩大之后,算法的识别率得到了很大程度的提高。对比图8(b)和图9(b),由于三角形搜索范围的增大,导致搜索时间变长,但是依然可以实现快速识别。
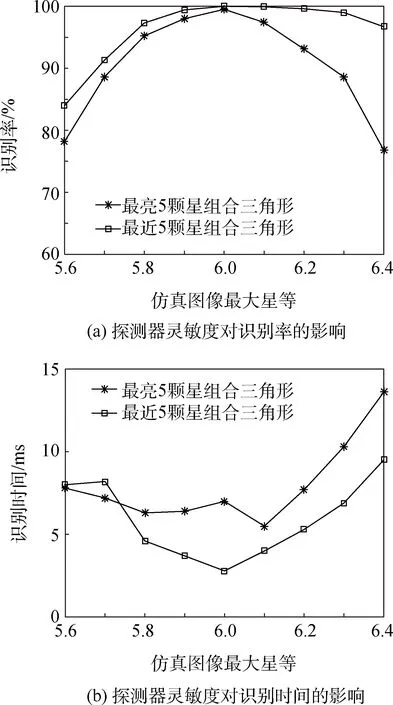
图8 不同最大星等值下的识别效果Fig.8 Recognition under different maximum star magnitudes
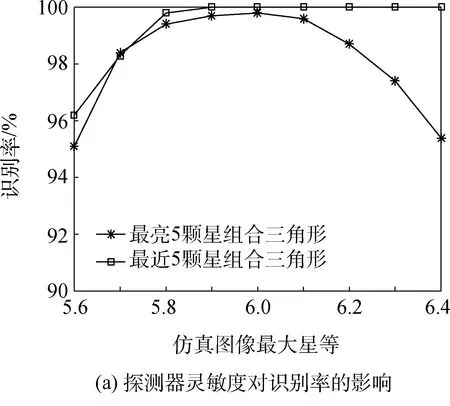
图9 改进后不同最大星等值下的识别效果Fig.9 Recognition under different maximum star magnitudes after improvement
续图9Fig.9 Continued
5 结束语
本文提出了一种结合SOM网络及三角形算法的星图识别方法,分析比较了迭代次数、分类总数、特征向量维度对识别时间及识别率的影响,并对组合三角形的两种选取方法进行了比较。相对于经典的三角形算法,本算法:1)搜索范围小、识别速度快,由于本文通过SOM网络对星表进行了预分类,每类的恒星较少,如分成81类时每类包含恒星不超过170颗,应用三角形算法时,搜索更快,系统识别时间平均在5 ms内。2)抗噪性能好,由于SOM网络良好的分类能力,当图像引入噪声带来位置和星等误差时,系统依然能较好的对恒星进行分类并识别出其对应的导航星,在噪声标准差为0.025时仍可达到99%的识别率。3)由于算法原理依赖于恒星的分布特点,对探测器的灵敏度改变较为敏感,在进行算法改进后,识别率得到了很大的提高,而相应产生的时间代价依然可以接受。

