基于差分进化算法的导航星座在轨重构构型设计
,,
1.航天工程大学 研究生管理大队,北京 101416 2.航天工程大学 航天装备系,北京 101416
当星座的空间部署完成后,其空间构型并非一成不变。当系统故障或是空间碎片撞击而导致星座中的卫星失效时,星座的服务性能必将大打折扣,此时修复星座性能的方式一般通过补发新的卫星来替换失效卫星,但由于受到新卫星研制周期、生产成本以及发射窗口的限制,该方法不可能在短时间内快速恢复受损星座的服务性能。此时若能对星座中未失效卫星进行轨道机动来调整星座构型,最大程度地修复和改善星座对目标区域或重点区域的服务性能,将显得尤其重要[1]。
针对星座中出现失效卫星且不存在备份卫星的情况,文献[2]针对连续多颗卫星失效的情况,以最大不可视时间为评价指标,提出了调整相邻卫星、均匀相位和均匀星座3种星座重构策略综合考虑燃料消耗和重构时间,提出了以总重构时间最小为优化目标的卫星星座快速重构构型优化设计方法。文献[3]针对全球卫星导航系统在部分卫星失效的情况下,通过调整剩余卫星的轨道进行星座重构,达到降低失效影响、优化地面导航性能的目的。文献[4]研究了将GPS从6轨道面变换到3轨道面时,对星座性能影响最小的构型变换重构控制策略。文献[5]研究了混合导航星座的中高轨道子星座重构策略和同轨道面内重构的方法,分析了重构优化目标与方法。文献[6]研究了导航星座中部分卫星失效后对星座性能的影响,提出了利用高、中、低轨卫星及临近空间飞行器进行任务重构的方法。
综合前人的研究成果,本文以建成后的北斗卫星导航系统为研究对象,针对星座中有卫星失效的情况,通过对在轨卫星进行相位机动的方式来实现星座构型的重构。重点从重构构型优化模型的建立、求解以及仿真等3个方面,对导航星座中有卫星失效的重构构型设计问题进行分析。建立了共面轨道相位机动的数学模型,并总结出了不同情况下相位机动中存在的规律,建立了除重构时间、重构能量外新的重构指标,并以此为目标函数对重构构型进行优化。
1 轨道机动模型与重构指标
1.1 轨道机动模型
为了使重构后的星座能够在长期运行过程中保持相对稳定的空间构型,本文在对星座中卫星的轨道参数进行调整时,仅改变卫星的相位角,即卫星在轨道上的位置,其他参数保持不变。根据调相过程中是否涉及轨道面间的机动,将卫星相位调整方式分为共面轨道相位机动和非共面轨道相位机动。考虑到非共面变轨和共面变轨在能量消耗上的显著差异,本文选择共面轨道相位机动的方式来改变星座中卫星的相位角。共面轨道相位机动又分为共面低轨变相和共面高轨变相。
(1)共面低轨变相
初始位置与目标位置之间的位置关系可以分为相位超前与相位滞后两种。从初始位置沿着卫星在轨道上的运行方向到目标位置所转过的角度为θ,
(1)
如图1所示,针对相位超前的情况利用低轨变相的方法来调整卫星在轨道上的相位角。
图中原始轨道为圆轨道其轨道半长轴为a0,转移轨道的轨道半长轴为a,初始位置和目标位置的真近点角为f0、f。位于初始位置的卫星施加一次冲量后进入转移轨道,当卫星在转移轨道上运行数圈后,位于目标位置上的卫星正好运行到初始位置,此时再施加一次冲量使卫星从转移轨道进入原始轨道,卫星在原轨道上的真近点角由f0变成f。
第一次变轨时,卫星在原轨道上的速度为v1,卫星进入转移轨道后的速度为v2,
(2)
式中:μ为地球引力常数。
第一次变轨和第二次变轨的速度增量分别为Δv1和Δv2,完成相位调整所需要的总能量用ΔV表示,
(3)
这一过程中,位于初始位置的卫星在转移轨道上等待的圈数为Ntra,位于目标位置的卫星在原始轨道上运行的整圈数为Norg,完成相位调整所需要的总时间为ΔT,有:
(4)
式中:θ的取值由初始位置和目标位置的真近点角而定;因为是低轨变相,所以转移轨道的半长轴a必须满足:
(5)
式中:Re为地球半径。
假设在星座重构过程中具备同时调整两颗及以上卫星的能力,对于整个星座而言,完成重构所需要的总能量和总时间用Vrec和Trec表示:
(6)
式中:i∈Satadj,Satadj为被调整卫星的编号集合;ΔVi和ΔTi分别为所调整卫星中编号为i的卫星完成重构所需要的总能量和总时间。
(2)共面高轨变相
对于共面高轨变相而言,其完成相位调整所需总时间ΔT和总能量ΔV的表达式皆与低轨变相相同,在此不再赘述。与低轨变相的区别在于转移轨道的半长轴所满足的约束条件不同,对于高轨变相而言有:
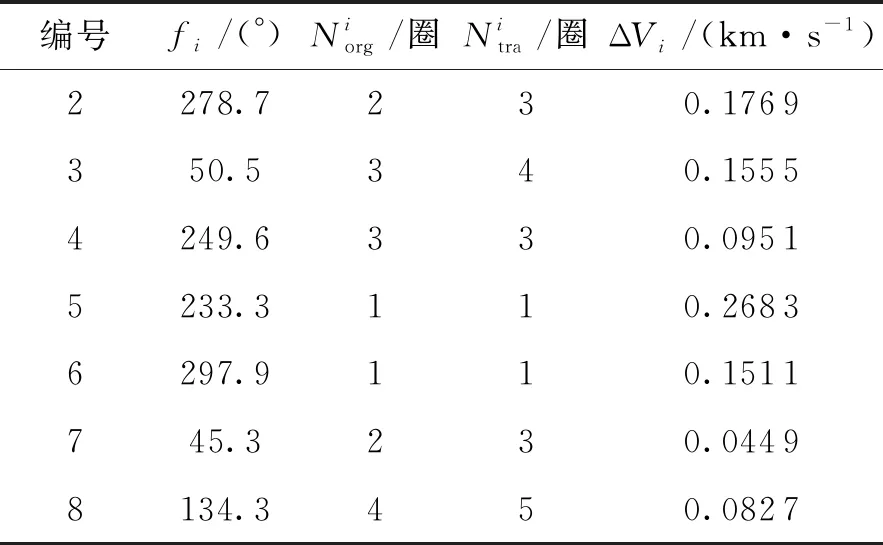
a0 (7) (3)调相方式的选择 理论上共面低轨变相和共面高轨变相两种共面轨道相位调整方式都可以解决相位超前和相位滞后的情况,但在实际问题中,综合考虑机动时间和机动能量,一般对于相位超前采用共面高轨变相,相位滞后则采用共面低轨变相[7]。除此之外不同相位调整方式中还存在其他的规律。 假设现将北斗卫星导航系统中某MEO卫星的真近点角从60°调整至30°(相位超前)和90°(相位滞后),设定完成相位机动所需的时间ΔT≤4d,利用上文建立的相位机动模型,得到相位超前下共面高轨变相和相位滞后下共面低轨变相两种情况下的所有调相策略,如图2、图3所示。 从图2中可以看出:对于相位超前而言,在机动时间不同的情况下,即Norg取不同的值时,对应的共面高轨变相的所有机动策略中,当ΔV最小时均满足Ntra=Norg。 从图3中可以看出:对于相位滞后而言,在机动时间不同的情况下即Norg取不同的值时,对应的共面低轨变相的所有机动策略中,当ΔV最小时均满足Ntra=Norg+1。 重构指标是用来描述重构构型的量化数据,目前针对于星座重构构型设计问题考虑最多的就是重构的时间和能量,这两个指标固然重要,但也不能全面的评价重构构型和重构过程的优劣和好坏,除此之外还应该考虑的指标有重构后星座的性能指标、重构能量的均衡度、以及重构构型的健壮性等。 (1)导航星座精度因子 对于导航星座而言,最关心的就是其定位精度。而定位精度除了受到各伪距测量值的影响还取决于星座的空间构型[8]。该构型可以用一个标量来表示,在导航领域中一般称为精度因子[9](Dilution of Precision,DOP)。DOP值的大小与定位误差成正比,理论上DOP值越小,定位误差越小,定位精度越高。 DOP值又可以分为GDOP(几何精度因子)、PDOP(位置精度因子)、HDOP(水平精度因子)、VDOP(垂直精度因子)和TDOP(时间精度因子)。本文选用GDOP值作为衡量导航星座定位精度的指标,分析某一时段内导航星座对目标区域的定位精度时,选用目前航天工程中运用最广泛的一种数值分析方法——网格点法。考虑到GDOP值是一个随时间和空间而变化的量,本文通过对目标区域内的所有网格点每一时刻的GDOP值进行统计,得到仿真时段内目标区域GDOP值的平均值,并用该统计量来表示导航星座对目标区域的定位精度。 (2)重构能量的均衡度 重构能量的均衡度是描述不同卫星完成重构任务所消耗能量的一致性,该指标越小说明重构过程中各卫星消耗的能量越均衡。重构过程中不同卫星所消耗推进剂的不同,往往会造成重构后卫星机动能力的差别,这不仅会使得星座中卫星的工作寿命参差不齐,还会影响重构后星座的整体服役时间。重构能量的均衡度用Prec表示,其大小为所有参与重构的卫星所消耗能量的方差: (8) (9) (3)重构构型的健壮性 重构构型的健壮性是衡量重构后星座的降阶使用能力,该指标越小说明重构后的星座抵抗卫星失效情况的本领越强。建立该指标是期望通过重构不仅使得星座性能得到恢复和提升,也希望当星座中再出现卫星失效的情况时,星座性能不会出现大幅度的下降。对于一个在轨运行的导航星座而言,如果不是非合作目标的故意破坏,同时出现多颗卫星失效的概率微乎其微,本文在衡量重构构型的健壮性时,以单颗卫星失效下的星座性能为参考,重构构型的健壮性用Srec表示: (10) 重构构型直接决定了重构后的星座性能,与星座构型设计一样,重构构型设计也属于多目标优化问题[10],但与星座构型设计不同的是重构构型设计所需要考虑的因素一般有重构后星座性能的提升程度,重构过程中的时间和能量消耗等;而星座构型设计考虑的则往往是星座的研制成本、发射代价、星座的服务性能、星座的运营和管理成本等。 (1)优化变量 (2) 目标函数 目标函数的构成直接决定了算法的收敛方向。确定目标函数的构成就是确定目标函数中包含哪些指标[11]。对于星座构型重构问题,本文选择的目标函数有:GDOPave目标区域的平均GDOP值;Vrec重构能量;Prec重构能量的均衡度;Srec重构构型的健壮性。 (3)约束条件 设定在基于轨道机动的导航星座重构构型设计中的约束条件为:相位超前时(θ∈(0,180°))选择共面高轨变相,且有Ntra=Norg;相位滞后时(θ∈[180°,360°))选择共面低轨变相,且有Ntra=Norg+1。除了机动过程中的约束,本文还将重构时间Trec也作为约束条件。 (1)差分进化算法的一般流程 差分进化算法(Differential Evolution,DE)自1995年由Kenneth Price和Rainer Storn发表以来,一直被誉为一种非常高效的全局优化器,在处理连续或离散参数的全局优化问题上得到了广泛的应用[12]。DE算法的实现步骤主要包括初始化、变异、交叉和选择,算法的实现过程如下: Begin 初始化参数: 种群规模Np,交叉概率Cr, 缩放因子F,最大迭代次数gmax g(种群代数)=0 产生初始种群:Pg=(X1,g,X2,g,…XNp,g) 评价初始种群: f(Pg)=[f(X1,g),f(X2,g),…,f(XNp,g)] While不满足终止条件, Do Fori=1:Np End for g=g+1 End While 输出最优结果 End (2)基于Pareto占优的选择准则 与单目标优化问题不同,多目标优化问题通常不存在一个能满足所有目标同时取得最优值的理想解,优化某一目标的同时通常会以劣化其他目标为代价,其求解过程实际上是一个不断权衡和折中的过程,针对这一问题本文引入了Pareto优化方法。 假设可行解x1对应的目标函数值中没有一个值大于且至少有一个值小于可行解x2的目标函数值,则称可行解x1相比于x2占优或x1支配x2: (11) 可行解x不被可行域S内的其他解所支配,则称该可行解为Pareto最优解,所有非支配解所组成的集合称为Pareto最优解集,Pareto最优解集在目标函数空间中的存在形式为Pareto前沿[13]。在差分进化算法中利用Pareto占优方法对试验向量和目标向量进行选择,最终可以将种群驱使到Pareto前沿: Xi,g+1= (12) (3)维数可变优化问题的编码方式 基于轨道机动的导航星座重构构型设计问题是一个维数可变的优化问题,被调整的卫星数直接决定了染色体的长度,对于差分进化算法而言,不同长度的染色体之间无法直接进行变异和交叉等操作[14]。为此本文采用分层编码的方式,对变量进行编码,如图4所示。 以建成后的北斗卫星导航系统为对象,星座中包含了35颗,其中:3颗IGSO卫星分布在3个轨道倾角为55°的同步轨道上,交叉点地理经度为东经118°,且3颗卫星的星下点轨迹相互重合,相位角相差120°;5颗GEO卫星的定点经度分别为东经58.75°、80°、110.5°、140°、160°;27颗MEO卫星均匀地分布在3个轨道倾角为55°的圆轨道面内,轨道高度为21 500 km。假定北斗卫星导航系统中的MEO卫星全部失效,现对其余3颗IGSO卫星和5颗GEO卫星进行在轨重构,仿真时间为[1 Jan 2020 00:00:00.000 UTCG]~[8 Jan 2020 00:00:00.000 UTCG],根据北斗卫星的构形参数设定1 Jan 2020 00:00:00.000北斗卫星导航系统中GEO、MEO卫星的空间位置如图5所示,并对星座中剩余卫星进行编号。 目标区域为亚太区域(东经55°~东经180°,南纬55°~北纬55°),重构时间Trec≤5D,初始种群的规模为100,缩放因子为0.9,交叉概率为0.5,最大迭代次数为50。 (1)减少重构能量 选择GDOPave和Vrec为目标函数,得到该优化问题的Pareto前沿如图6所示。 (2)降低重构能量均衡度 选择GDOPave和Prec为目标函数,得到该优化问题的Pareto前沿如图7所示。 表1 减少重构能量下的卫星重构策略 编号fi/(°)Niorg/圈Nitra/圈ΔVi/(km·s-1)2278.7230.1769350.5340.15554249.6330.09515233.3110.26836297.9110.1511745.3230.04498134.3450.0827 (3)增强重构构型健壮性 选择GDOPave和Srec为目标函数,得到该优化问题的Pareto前沿如图8所示, 图8中GDOPave的取值范围为[2.749 0,3.492 9],Srec的取值范围为[1,4.900]。当GDOPave=2.749 0时对应的上层染色体(S1,S2,S3,S4,S5,S6,S7,S8)=(0,0,0,1,0,1,1,1),即有编号为4、6、7、8的卫星参与重构,且f4=68.0°,f6=49.4°,f7=251.9°,f8=49.4°,只有当重构后星座中编号为1的卫星失效时,星座性能受到的影响最大,此时GDOPave达到13.470 1;当GDOPave=3.492 9时,与重构前相比,星座性能提升了18.1%,对应的上层染色体(S1,S2,S3,S4,S5,S6,S7,S8)=(1,1,0,1,0,1,1,0),即编号1、2、4、6、7的卫星参与重构,且f1=175.3°,f2=267.6°,f4=188.5°,f6=128.7°,f7=194.2°,只有当重构后星座中编号为1的卫星失效时,星座性能受到的影响最大,此时GDOPave达到265.037 7。 本文建立了包括重构能量、重构时间、重构能量均衡度、重构构型健壮性以及星座性能指标在内的重构指标模型,并以此为目标函数对重构构型进行优化,但本文仅分析了对在轨卫星进行相位机动的方式来提升和恢复受损导航星座性能的方法,除此之外,还有利用快速发射系统增发卫星和借助其他导航星座形成组合导航系统来增强受损导航星座性能的方法[15]。而这正是作者接下来要研究的内容。1.2 重构指标

2 差分进化算法在重构构型设计中的应用
2.1 重构构型优化模型
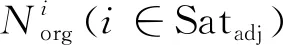
2.2 差分进化算法

3 仿真算例
3.1 算例描述
3.2 仿真结果分析
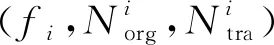
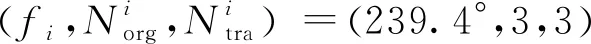

4 结束语

