考虑磨损后含间隙指向机构运动特性

，,*，，

1.燕山大学 河北省并联机器人与机电系统实验室，秦皇岛 066004 2.燕山大学 机械工程学院，秦皇岛 066004

空间指向机构在哈勃望远镜、空间光学相机、星载数传天线等航空航天设备中具有广泛的应用，实现对目标的实时跟踪、扫描、定位等功能。指向机构的性能对接收信息的稳定性和成像质量有很大影响。运动副间隙、摩擦磨损等因素对机构工作影响较大，它会降低机构运行精度，使其运行轨迹发生非线性波动，机构发生颤动等现象，因此研究计及运动副间隙、摩擦磨损等因素对空间指向机构的影响，在航空航天技术的发展领域具有重大意义。文献[1]对空间双轴指向机构的指向速度、加速度、精度等参数指标进行了试验研究，分析了其运动性能。文献[2-3]建立了一种含轴向尺寸的线接触碰撞铰模型，在此基础上提出一种改进的非线性法向碰撞力模型和修正的切向库伦摩擦力模型，对机构动力学性能进行研究。文献[4]在可展结构的运动副中引入间隙，采用修正的库伦摩擦力模型，分别计算了含间隙转动副元素之间的法向与切向接触力，将关节间隙效应引入到可展结构中。

文献[5-6]以含间隙双轴机构动力学分析结果为基础，计算得到了间隙运动副副元素的动态磨损量，最后分析了含间隙双轴机构的动态特性。文献[7]提出了非累积性因素和累积性因素耦合作用下平面机构的运动精度可靠性仿真试验方法。文献[8]建立了含多间隙曲柄滑块机构的动力学模型，并进行动力学特性分析，应用Archard磨损模型对间隙运动副的磨损进行了预测。文献[9]基于无质量杆-弹簧阻尼模型建立了系统动力学分析模型，提出了一种新的含间隙铰接副磨损分析方法。文献[10]通过集成柔性多体动力学与磨损计算程序，提出了一种用于对柔性多体系统中间隙铰接副部位的磨损进行了预测的方法。文献[11]考虑接触过程中销轴和孔的接触面曲率半径变化趋势，建立了磨损仿真模型。文献[12]以某卫星天线双轴驱动机构为研究对象，分析旋转铰在系统运行中的磨损规律。文献[13]对考虑间隙机构的转动副进行了磨损计算，并分析了间隙增大对系统动态特性的影响关系。文献[14]对空间高精度指向机构进行实验研究，观察了二硫化钼固体润滑涂层磨损情况，分析了力矩波动与输出精度。

现有的相关研究大多是采用试验方法对选定机构静态时的磨损进行分析，因忽略动态因素的影响，研究结果与实际情况有一定差异。因此，有必要对动态时接触碰撞力、相对滑移速度和动态磨损特性进行研究。

本文研究了含间隙空间二维指向机构运动副发生磨损以后的动态特性，并进一步预测了机构的使用寿命。研究工作为提高指向机构的使用性能与应用奠定基础。

1 机构结构及动力学模型

1.1 指向机构结构

如图1所示，二维指向机构由摆镜、U形架、电机、谐波减速器、同步感应器轴系(体1、体2)与关节组成，其中轴系包括俯仰轴系和方位轴系。

一般来说，要求机构的整体质量小，且悬臂尽可能短，以减少整个卫星质量，减少支点的悬臂力矩。因此，各主要组成部分尽可能轻量化。

1.2 动力学模型

假设将二维指向机构视为刚体，不考虑驱动电机的间隙非线性影响。

建立坐标系如图2所示。其中，O0-x0y0z0为二维指向机构的基坐标系，即为{0}坐标系；坐标系O1-x1y1z1和O2-x2y2z2分别固定在关节1和关节2转轴上，即为{1}坐标系和{2}坐标系。其中，各关节分别绕z1轴和z2轴转动，角位移为θ1和θ2；B点为末端上的点；irci为各体质心关于{i}中的位置矢量；Bp表示点B在基准坐标系中的位置向量。体i(i=1,2)的长为Li，体i的质心Si(i=1,2)到第i个轴质心的距离为LSi，体i的质量为mi，体i绕第i个轴转动时的转动惯量为Ji，设作用在体i上的驱动力矩为Ti。

(1)运动副的数学模型

如图3所示，含间隙转动副的转轴中心点移动距离为：

(1)

式中：eix为ei在x方向投影；eiy为ei在y方向投影。

轴心在含间隙转动副中方位角φi为：

(2)

内部接触碰撞产生的穿刺量为：

δi=ei-ci

(3)

式中：ci初始间隙值。

由于机构转动副均具有间隙，在关节2处建立过渡坐标系{A}，如图4所示。原点位于关节2轴套中心位置。

建立多体系统齐次变换矩阵为：

(4)

(2)接触碰撞力

采用非线性弹簧阻尼模型来描述运动副内接触碰撞力[15]，其广义形式为：

(5)

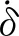
(3)切向摩擦力

采用修正的库伦摩擦力模型来求解运动副间切向摩擦力[16]，其表达式为：

Ft=-μtcdFn(νt/vt)

(6)

式中：μt为滑动摩擦系数；cd为动态修正系数。

(4)广义力

采用牛顿欧拉方程，正向求解各体质心处的惯性力和惯性力矩，然后在从末端逐次向基座反向求解各转轴所受的力和力矩，写成矩阵形式。

(7)

其中，矩阵M*中各变量皆为与θ1、θ2相关的参数，在此不再赘述。

各关节的力矩T的表达式为：

2 机构动态磨损特性分析

接触表面磨损时，会导致运动副间隙进一步增大，且磨损后运动副工作面形貌呈非规则变化。下面研究考虑磨损后的机构动力学特性。

2.1 动态磨损计算模型

Archards模型为：

(8)

式中：Ka为磨损系数；N为法向接触载荷；H为材料的硬度；V为磨损量；S为滑移距离。

将上式转换成微分形式，其为：

(9)

2.2 磨损量计算

利用磨损计算模型式(9)，计算磨损量，计算流程如图5所示。

通过分析可知，在任何工况下，空间二维指向机构关节1都比关节2更容易失效，所以以下研究主要针对关节1来进行分析。体1杆长L1为0.5 m，质心LS1为0.257 7 m，质量m1为3.672 5 kg，惯量JO1为0.440 8 kg·m2，关节1轴套半径R1为0.050 2 m，轴半径R3为0.05 m；采用参数摄取法，提取关节1处的接触碰撞力，代入式(9)求解，式中Ka、H为与材料特性有关的参量，由试验数据获得[17]Ka=9.956×10-8，H=1.71×109时，其磨损量仿真结果如图6所示。

由图6可知，当运动副之间没有相对运动时(即t=0时)，磨损量为零；当产生相对运动时，磨损量发生变化。

2.3 一次磨损深度计算

假设运动副工作面上的磨损量已知，那么相同接触材料的磨损深度只与接触区域的面积有关。考虑h/s代表任意时刻的磨损率，磨损模型可写为：

(10)

式中：h为磨损深度；P为接触碰撞压强。

接触长度是一个和穿刺深度有关的变量，由于它的值很小，本文采用穿刺深度的2倍来表示接触长度，轴承宽度为d=27mm，运动副的磨损深度变化曲线如图7所示。

由图7可知，磨损深度曲线随时间波动较大。原因为：一是由于接触时间一般比较短；二是由于对关节施加的驱动力矩是变化的，且运动副副元素间接触力呈非线性。

2.4 轮廓重构

将转动副在极坐标内分成若干个区间，不同时刻的接触点落在ds区域内。把每次落在ds区域内的磨损深度进行叠加，即可得到运行一段时间后ds区域的磨损深度。若运动部分接触n次，将转动副上各区域内不同时刻发生接触时的磨损深度叠加，如图8所示。则该区域磨损深度为：

(11)

转动副工作面不同位置与叠加后的磨损深度关系如图9所示。考虑磨损后，工作面轮廓重构步骤为：

1)将磨损前运动副半径叠加上各点的磨损深度，得到新的曲线圆半径；

2)确定磨损后的表面形貌；

3)重构转动副工作面轮廓。

图10为重构后的工作面轮廓。从图10可知，转动副的磨损深度不同，呈非线性变化，这是由机构运动速度和碰撞力的非线性变化造成的。

2.5 磨损后机构动态特性分析

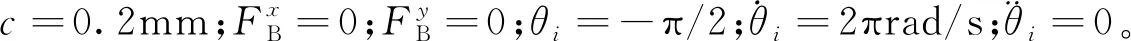
图12、图13分别为关节1在考虑磨损后和理想情况下的接触碰撞力、切向接触力变化曲线。在考虑磨损情况下，随着输入驱动变化，碰撞力所产生的波动更加明显，峰值更大，且波动发生时刻要滞后于理想情况；切向摩擦力峰值变大，波动也更加明显。上述情况主要是因为磨损使运动副工作面呈现出非规则形貌，存在很多突起或凹陷，极大的增加摩擦力，降低了机构的稳定性。

3 机构磨损寿命预测方法

为了加快磨损寿命预测模型运算效率，将机构整个运行过程分为若干阶段，每一段运行时间中的接触力和相对滑移速度采用拟合函数代替。将相应函数带入式(9)中，建立动态的磨损数学模型。

3.1 建立拟合函数

(1)接触碰撞力随间隙变化公式拟合

基于第1.2节含间隙空间二维指向机构动力学模型，给定驱动力矩T1=0.5sin(πt) N·m；T2=0.2sin(πt) N·m，分析间隙值为0.1、0.2、0.3、0.4、0.5时的接触碰撞力变化情况，并进行对比。

图14为间隙大小不同时关节1碰撞力的变化情况。关节碰撞力在某些时段发生交替突变，而且随着间隙值的增大，突变时间会有所延迟，突变峰值也随着变大。

提取不同间隙时内部接触碰撞力数组的中位数，拟合其碰撞力的变化曲线。如图15所示，拟合工具采用1阶线性拟合。

随着磨损间隙值越变越大，碰撞力也越来越大，间隙值与碰撞力近似成正比例关系。接触力Fn与间隙c的函数关系更接近于线性关系，其表达式为:

F1=K1c+B1

(12)

式中：K1为碰撞系数；B1为初始碰撞力。

(2)相对滑移速度随时间变化公式拟合

同上可知，两关节在给定角速度时，可以得到不同间隙下运动副碰撞力的变化情况；当两关节角速度都为ω=2πrad/s时，不同间隙碰撞力变化的拟合曲线如图16所示。

接触力Fn与间隙c的函数关系表达式为:

F2=K2c+B2

(13)

式中：K2为碰撞系数；B2为初始碰撞力。

建立速度随时间变化的计算公式为：

(14)

在给定运转角速度为ω=2πrad/s时，关节1相对滑移速度公式如下：

(15)

3.2 磨损失效寿命预测

以机构的关节为目标，研究其磨损失效寿命，其分析流程如图17所示。根据二维指向机构的动力学模型和动态磨损模型分别计算碰撞接触力和磨损量，运行结束后，将产生的磨损深度叠加到间隙值上，在基于叠加后含间隙机构的关节接触力计算下一时间段的磨损深度，如此循环将每一时间段所产生的不同磨损深度叠加即可得到最终的间隙值。

利用含间隙运动副内部间隙值与接触力之间的对应关系，运行时间与相对滑移速度之间的对应关系，拟合上述关系，得到拟合函数，设定当机构运动失效时相应的运动副间隙值作为磨损失效阈值，求解运算流程如图18所示。

建立二维指向机构的寿命预测数学模型:

δN+1=δN+HN+1

(16)

式中：δN+1为第N+1次磨损后的间隙值；δN为第N磨损前的间隙值；HN+1为第N+1磨损深度。

(17)

式中：p为压强；S为转动副工作面面积。

基于动态磨损计算模型，通过Matlab计算出间隙值大于失效阈值时的迭代次数，将迭代次数转换为运行时间即可得到磨损寿命。最终成功预测了卫星天线二维指向机构的使用寿命。

4 计算实例

以空间二维指向机构关节1为研究对象，由于指向机构的运动模式主要分为跟踪和调姿两种模式，所以需要计算指向机构在两种模式下的磨损寿命。星载天线等高精密空间指向机构中转动副间隙值大于0.5 mm时机构将会发生故障，将其设为失效阈值[18]。

1)跟踪模式时，初态下，在各关节处分别施

加驱动力矩T1=0.5sin(πt) N·m；T2=0.2sin(πt) N·m。

根据式(13)、式(14)可以求得：

①滑移速度拟合公式，

vt= 1.69×10-2-1.773×10-2cos(πt)-

5.417×10-4sin(πt)

(18)

②碰撞力的拟合公式，

Fn=84 176.582 278 772 9c+0.607 671 378 757 530

(19)

在跟踪模式下，机构关节1间隙值与运行时间的变化曲线如图19所示。根据磨损计算流程，上述运行速度为一个非线性变化量，运行开始到结束转动次数为2 833 183次，运行时间为12 591.92 h。

2)调姿状态时，当给定角速度为ω=2πrad/s时，相对滑移速度拟合公式为：

0.004 629 sin(98.58t)

(20)

调姿模式下，关节1内间隙大小与运行时间的变化曲线如图20所示。根据磨损计算的流程，运行一周所需时间约为1 s，所以取迭代一次的计算微元为1。运行2 751 974次后，间隙达到了阈值规定的数值。运行时间为764.44 h。

5 结束语

本文综合考虑间隙、磨损等因素，通过牛顿-欧拉法和Archards模型建立了含动态磨损间隙的动力学模型并进行磨损特性分析，针对空间指向机构进行磨损寿命预测，得出如下结论：

1)磨损间隙对角位移影响比较小，而对角速度和角加速度影响比较大，尤其是角加速度；

2)磨损后的接触碰撞力和切向摩擦力比磨损前的波动明显，峰值比例在3倍左右，磨损不利于机构的稳定性；

3)接触力和相对滑移速度采用拟合出的线性函数代替，基于动态磨损计算模型，得到了机构关节在两种姿态下的磨损寿命。