二维MT电阻率与磁导率同时反演研究

张志勇，谢尚平，李 曼,2，马 鑫，李 万

(1.东华理工大学 地球物理与测控技术学院，江西 南昌 330013；2.同济大学 海洋与地球科学学院，上海 200092)

磁法勘探中，磁化率(κ=μr-1)变化是引起磁异常的重要原因(其中μr=μ/μ0，为无量纲参数)；对磁测数据进行磁化率反演的研究工作在生产实践中得到了广泛应用(Abedi et al., 2013; Li et al., 1996; Pilkington, 1997; Portniaguine et al., 2000)。然而，大地电磁勘探一般只考虑介质电阻率变化，并假设地下磁导率(μ)为常数，等于真空中的磁导率(μ0=4π×10-7H·m-1)。但在实际勘探环境中，岩石的磁导率随铁磁性矿物成分的增加而增大(Clark et al., 1991)，富含铁磁矿物的岩石磁导率明显高于真空中磁导率。近年来，为了提高数据处理质量充分挖掘信息，磁化率对电磁勘探的影响得到了关注(Farquharson et al., 2003; Cao, 2005; Sasaki et al., 2010; Müller et al., 2012; Van et al., 2013)。大地电磁同时反演电阻率与磁导率的研究表明，同时反演两个参数可以改善电阻率反演效果，同时岩石磁导率的获取也丰富了解释参数，提高了火成岩的成像效果(Cao et al., 2005)；磁偶源同时反演磁导率与电阻率的研究表明，对于包含磁导率异常的数据只反演电阻率会产生错误模型，同时反演两参数可以得到可信的电阻率模型和有用的磁导率信息(Farquharson et al., 2003)；但是，磁导率对频率变化依赖性小，单一高度的航空电磁数据同时反演电阻率与磁导率的效果较差，同时反演不同高度、不同线圈排列形式的数据可以得到更精确的结果(Sasaki et al., 2010)；海洋可控源电磁数据测量理论研究与实践表明，布设在海底的可控源电磁装置可有效进行浅海海底沉积物的电阻率与磁导率成像(Müller et al., 2012)；高频电磁测深(100 kHz～100 MHz)磁场垂直分量对介质电导率、磁导率、介电常数的灵敏度研究表明，该频段覆盖传导电流与位移电流的过渡带，对电阻率、介电常数、磁导率三个参数均较敏感(Müller et al., 2012)；对于更高频段，铁磁性介质对探地雷达波(n×10 MHz～ nGHz)的波速、反射及衰减均产生影响(Van et al., 2013)。

鉴于此，开展了同时考虑电阻率与磁导率的二维大地电磁正则化反演研究。通过正演模拟分析了磁导率变化对卡尼亚视电阻率及其相位的影响；建立了同时反演电阻率与磁导率的正则化反演目标函数，并通过高斯-牛顿法求解；采用函数映射将电阻率与磁导率映射到反演空间，将电阻率与磁导率限定在具有实际物理意义的变化区间，通过双共轭梯度稳定算法求解高斯-牛顿方程，确保反演稳定性。开展了合成数据与实测数据的反演工作，表明从大地电磁数据可以恢复地下介质磁导率，同时反演磁导率与电阻率提高了反演效果，丰富了大地电磁数据解释的依据。

1 二维大地电磁电阻率与磁导率影响模拟

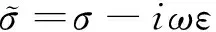
(1)

(2)

式(1)代表E型波(也称TE模式)，式(2)代表 H型波(也称TM模式)。二维大地电磁问题可以通过有限单元方法求解(Wannamaker et al., 1986; De Lugão et al., 1997; Sheen et al., 2000; Key et al., 2006; 刘云等2010; 张志勇等, 2013, 2015)。

为确定磁导率对卡尼亚视电阻率及其相位的影响，进行图1所示模型试算(张志勇等，2013)：在ρ0=100 Ω·m，μ0=4π×10-7H·m-1，ε0=8.854 2×10-12F·m-1的均匀半空间内设置三个截面为正方形(边长300 m)的二度体，二度体上顶埋深220 m，间距550 m。不考虑介电常数异常，M1异常体ρ1=50 Ω·m，μ1=2μ0，M2异常体，ρ2=100 Ω·m、μ2=2μ0，M3异常体ρ3=200 Ω·m、μ3=2μ0。在地表采用50 m点距进行大地电磁测量，观测频率范围为2-12～212Hz。

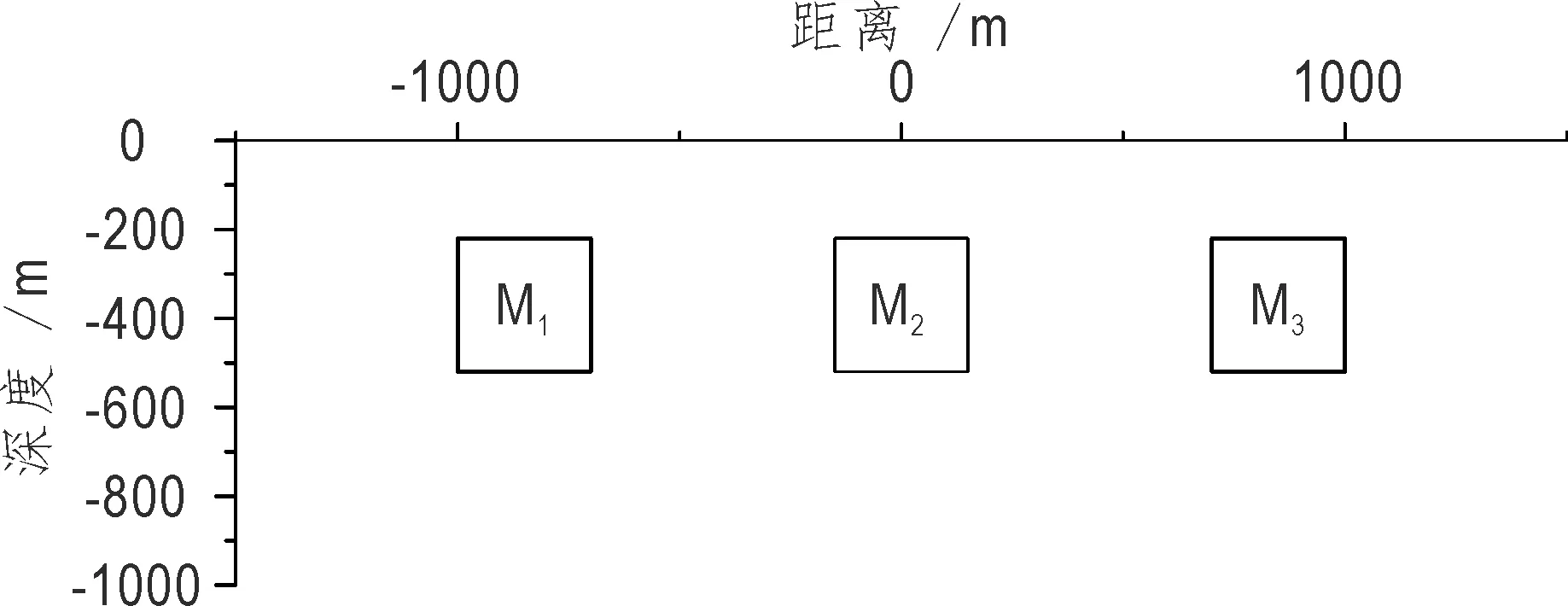
图1 试算模型Fig.1 Test model

同时考虑电阻率、磁导率变化条件下，图1试算型的计算结果如图2。由图2a可见TE模式视电阻率均为高阻异常，M1、M2引起的异常向低频发展不圈闭，形态类似于只考虑电阻率变化时高阻体TM模式响应；M3引起的异常成半圈闭并向低频发展开口。TE模式视相位(图2b)，形成上下两个圈闭异常且下部圈闭异常明显；M2、M3形成圈闭异常。TM模式视电阻率(图2c)，形成低阻向低频发展不圈闭异常，M3形成高阻向低频发展不圈闭异常；M2形成高阻圈闭异常；TM模式视相位(图2d)，M1、M2形成上下两个圈闭异常且下部圈闭异常比上部明显；形成圈闭异常。

图2 试算模型计算结果Fig.2 Contours of apparent resistivity and phase for test modela.TE模式视电阻率；b.TE模式视相位；c.TM模式视电阻率；d.TM模式视相位

地下电导率与磁导率的变化对视电阻率及相位均产生明显影响；受磁导率影响，TE模式异常形态向无磁导率影响TM模式形态转变，可能将低阻异常变为高阻异常；试算模型，磁导率对TM模式异常形态影响没有TE明显，低阻异常仍为低阻；只有磁导率差异的异常体会产生明显的异常，其TE模式的异常形态类似于无磁导率影响的TM模式的视电阻率异常。

2 同时反演电阻率与磁导率的正则化反演

数值模拟表明地下介质的磁导率差异可引起卡尼亚视电阻率异常，下面探讨采用正则化方法进行电阻率与磁导率的联合反演算法。

只考虑电阻率差异的大地电磁从一维到二维反演已发展成熟，三维正逐步进入实用阶段。一维反问题可采用奇异值分解方法进行迭代反演(Jupp et al., 1975)，Jupp等(1977)扩展了这一方法开展了二维大地电磁反演。为避免反问题的多解性，Constale等(1987)提出了著名的Occam反演方法，采用模型平滑约束进行一维大电磁与直流电阻率数据正则化反演。Occam反演在大地电磁数据反演中得到了广泛应用，在一维基础上发展了二维大地磁Occam反演(Degroot-Hedlin et al., 1990)；开展了数据空间DASOCC与缩减的数据空间REBOCC反演研究(Siripunvaraporn et al., 2000, 2009;Kordy et al., 2016)，利用二维与三维条件下大地电磁数据量一般远小于模型参数的情况来减少反演运算量。求取和存储灵敏度矩阵是正则化反演的关键问题，为减少计算量和内存需求开展了大量的研究工作：如假定电导率的水平变化远小于垂向变化，近似计算灵敏度矩阵的快速松弛反演(RRI)(Smith et al., 1991)；互换定理是减少灵敏度矩阵计算工作量的另一有效途径(Rodi, 1976; Jupp et al., 1977; Sasaki, 1989; De Lugão et al., 1996, 1997)；采用基于伴随方程计算灵敏度矩阵(McGillivray et al., 1994)，其计算量与结合了互换定理的灵敏度计算量相当，但采用均匀半空间解析解作为伴随方程解进行计算可大大减少计算量(Farquharson et al., 1996)；非线性共轭梯度法(NLCG)因为只需要计算灵敏度矩阵及其转置与向量的乘积，可避免直接存储灵敏度矩阵从而减少存储量，并最终将灵敏度矩阵及其转置与向量的乘积转换为正演计算(Newman et al., 2000,2003; Rodi et al., 2001; Zhdanov et al., 2004)。高斯牛顿法是另一种求解非线性反问题的有效方法，与非线性共轭梯度相比具有目标函数下降快、所需迭代次数少的优点；该方法的主要困难，一是灵敏度矩阵的计算、满阵乘法运算的计算量大，二是正则化反演得到的海森矩阵条件数大，求解困难(Sasaki, 1989, 2001; Usui, 2015)；通过迭代解法求解高斯-牛顿方程，可以采用NLCG类似的方法避免显式求解灵敏度矩阵，提高计算效率(Mackie et al., 1993; Grayver et al., 2013; Jahandari et al., 2017)。

研究工作构建了同时反演电阻率与磁导率的正则化反演目标函数，通过高斯-牛顿法求解反问题，实现了有限内存条件下大地电磁电阻率与磁导率同时反演。

2.1 同时考虑电阻率与磁导率的正则化反演目标函数

同时考虑电阻率与磁导率条件下，正则化问题目标函数定义为：

φ=φd+λρφp+λμφμ

(3)

其中数据误差，

φd=(G(ρ,μ)-dobs)TWdTWd(G(ρ,μ)-dobs)

(4)

式中，G(ρ,μ)为正演函数，dobs为观测数据，Wd为数据方差矩阵；φρ、φμ分别为电阻率、磁导率模型误差项，可统一表达为(Zhdanov, 2002)：

φρ=(ρ-ρapr)TWρTWρ(ρ-ρapr)

(5)

φμ=(μ-μapr)TWμTWμ(μ-μapr)

(6)

式中，ρ、μ分别为介质电阻率与磁导率，ρapr、μapr为参考模型的电阻率与磁导率，Wρ、Wμ为统一表示的电阻率与磁导率模型正则化矩阵；λρ=γλ、λμ=(1-γ)λ,λ为正则化因子,γ是平衡电阻率模型与磁导率模型正则化项的比例系数。

正则化因子选择可采用广义交叉验证准则(GCV)(Farquharson et al., 2003; Haber et al., 2000)、“L-Curve”标准(Hansen, 1992; Li et al., 2000)，本文工作采用修正的“L-Curve”算法(李曼等, 2014)。平衡系数对磁导率的反演影响很大(Farquharson et al., 2003)，Routh等(1998)进行频谱激电的Cole-Cole四参数反演时采用各参数正则化项的比值进行平衡，Loke等(2006)则通过灵敏度矩阵模的比值进行平衡。本文采用类似Loke的方法，通过下式计算平衡系数：

(7)

式中，Gρ、Gμ为观测数据对电阻率与磁导率的灵敏度，可采用互换定理快速计算(Rodi, 1976; Sasaki, 1989; De Lugão et al., 1996)。

为确保电阻率与磁导率在正常的岩石与矿物取值范围内，反演在变换域进行(Habashy et al., 2004; Commer et al., 2008; Key, 2009, 2016)。将电阻率、磁导率进行函数变换，设反演空间变量为x，m为模型空间变量且m∈(α,β)，则可采用如下变换关系，

(8)

(9)

(10)

采用迭代法求解正则化目标函数(3)，对第k+1次正演进行Taylor极数展开，可得

G(ρk+1,μk+1) =G(ρk,μk)+GρΔρ+GμΔμ+ο(Δρ,Δμ)

(11)

忽略二次以上高次项，代入式可得高斯-牛顿方程：

HkΔm=-φ

(12)

其中，

(13)

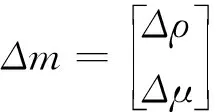
(14)

(15)

2.2 基于双共轭梯度稳定算法的有限内存优化

地球物理反问题得到的高斯-牛顿方程式，由于海森矩阵性质不好，如果采用直接解法求解该方程很难求得稳定解，很多学者采用正交分解或迭代解法求不完全解，如正交分解方法(Sasaki, 1989; Grayver et al., 2013)、共轭梯度法(CG)(Mackie et al., 1993)、广义最小余量法(GMRES)(Jahandari et al., 2017)。本次工作采用双共轭梯度稳定算法(BICGSTB)(Saad, 1996)迭代求解式。计算过程如下：

(2)p0:=r0.

(3)Forj=0,1,…,untilconvergene Do:

(5)sj:=rj-ajHkpj

(6)wj:=(HKsj,sj)/(Hksj,Hksj)

(7)Δmj+1:=Δmj+αjpj+wjsj

(8)rj+1:=sj-wjHKsj

(10)pj+1:=rj+1+βj(pj-wjHKpj)

(11)End Do

算法中有关海森矩阵与向量的乘积，可展开为灵敏度矩阵及其转置与向量的乘积，最终转换为正演计算，从而避免直接存储海森矩阵与灵敏度度矩阵，实现有限内存条下的反演计算(Mackie et al., 1993; Rodi et al., 2001)。

3 合成数据反演

对图1所示模型计算所得数据，加入3%的随机噪声，采用第二部分算法，进行试算，反演结果如图3b和图3c，并与只反演电阻率的反演结果(图3a)进行对比分析。

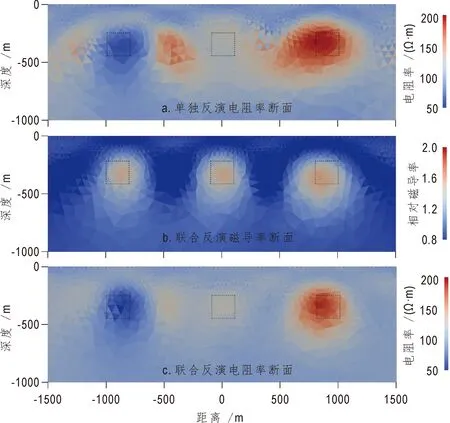
图3 合成数据反演结果Fig.3 The inversion result of synthetic data

由图3可见，反演算法成功得到了异常体的磁导率(图3b)和电阻率(图3c)。由于异常体磁导率的影响，单独反演电阻率(图3a)效果不理想，低阻、高磁导率异常体M1位置反演得到了一个低阻体，但其两侧出了高阻假异常；M2位置出现了略高于背景电阻率的异常；M3高阻、高磁导率位置，出现了大块高阻，高阻区远大于M3实际的空间大小，并受M2高磁导率异常的影响向其延伸。另外，由正则化因子、数据均方根误差、稳定因子随迭代次数变化曲线(图4)，可见研究工作采用的算法，数据均方根误差随迭代次数的增加稳定下降，同时反演电阻率与磁导率图4b可以得到更小的数据误差。研究作采用了渐进网格反演策略，网格细化过程重新设定正则化因子，所以正则化因子与模型误差变化曲线是分段平滑的，限于篇幅该算法另行讨论。

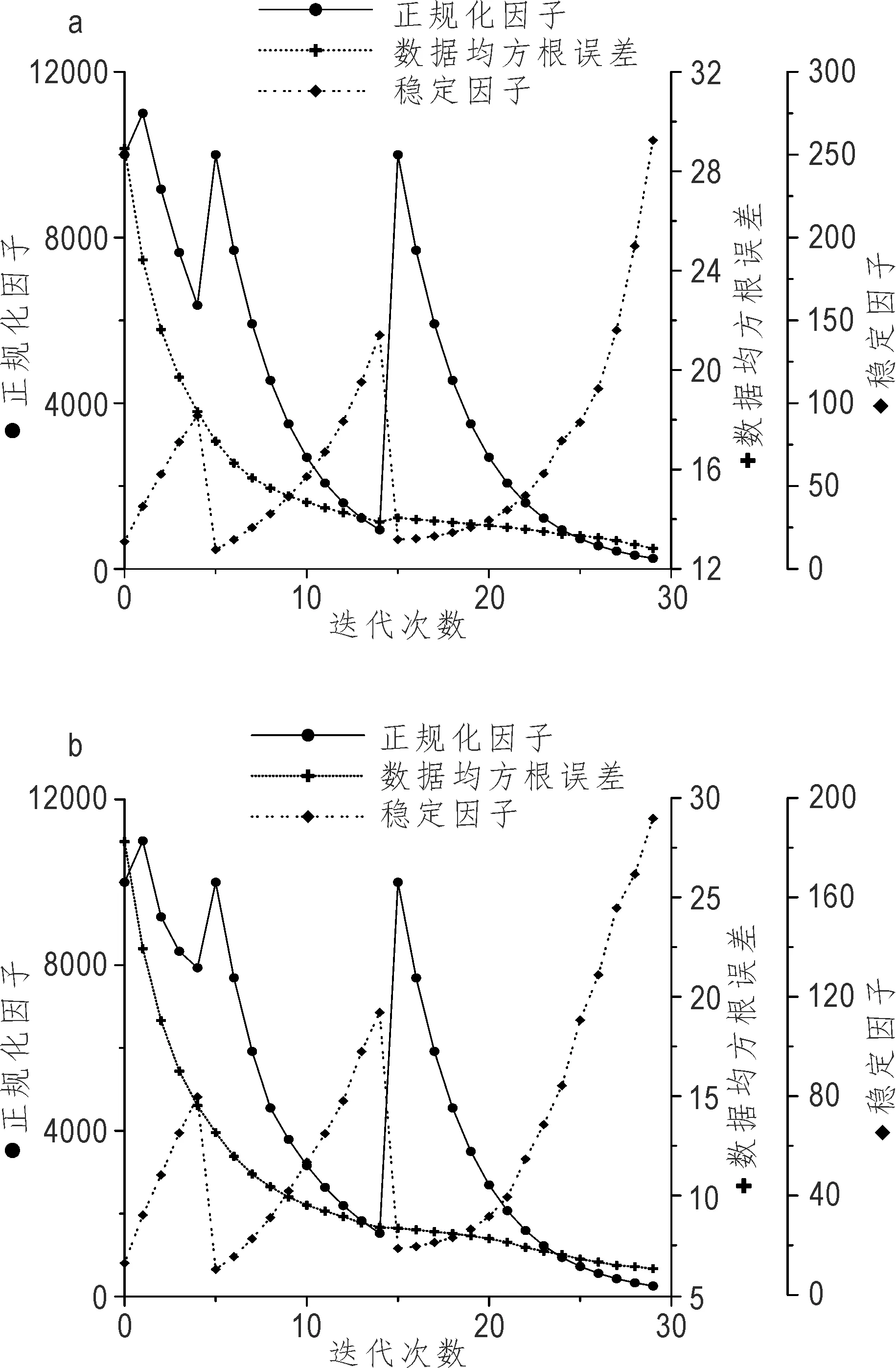
图4 正则化因子、数据均方根误差、稳定因子随迭代次数变化曲线Fig.4 Optimum Multiplier, Root mean square error, stabilizer variation curve with iteration timesa.直接反演；b.同时反演

4 某花岗岩区联合反演电阻率与磁导率实例

采用本文算法对某花岗岩区音频大地电磁数据进行了联合反演。反演剖面长度7 km，设计点距50 m，实际采集测点138个。勘探工作的主要目的是探测花岗岩内部的断裂构造带与辉绿岩脉。标本测试表明，该区花岗岩电阻率变化范围为4 200～8 000 Ω·m，辉绿岩电阻率一般高于12 000 Ω·m；花岗岩磁化率变化不明显，但辉绿岩磁化率明显大于花岗岩，相对磁导率可达约2.7；研究区湿润多雨，断裂构造与高阻围岩相比存在明显的电阻率差异。物性分析表明，该区存在电磁勘探的物性基础。

反演采用了所有138个测点数据，频率从6.9 Hz到10.4 kHz共42个频点。分别进行了单独反演电阻率(图5a)和联合反演电阻率与磁导率(图5b、c)的反演工作。总体上看，单独反演电阻率断面相比联合反演所得到的电阻率断面电阻率值要高，这与数值模拟计算结果相对应，高磁导率有类似于高阻的影响；单独反演得到的电阻率断面，岩体内部出现近水平的低阻条带状异常，很大部分与地质条件不符；联合反演得到的电阻率断面，浅地表低阻异常明显，对比地质断面低阻异常体与出露的断裂构造对应，同时揭示了多条隐伏构造。联合反演出的磁导率断面，以低值为主，并出现了几条由地表向深部发展的高磁化率局部异常，与辉绿岩脉对应；大于526 500 m的区域出现了大面积磁导率中高值区，推测相较断面其它区花岗岩完整性更好或者为不同期次侵入的花岗岩体；测线起点端，存在一长透镜状高磁化率区，推测与岩体内部铁磁性物质升高有关。

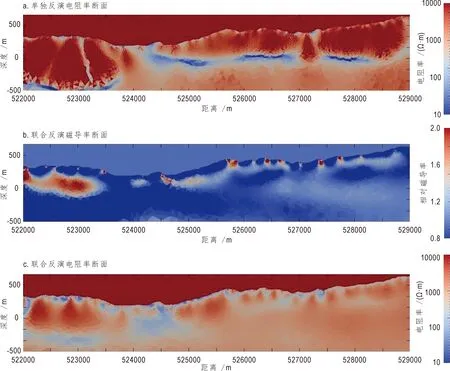
图5 某花岗岩区反演结果Fig.5 The inversion result of a granite area MT data

5 结论与建议

通过数值模拟，论证了磁导率异常对大地电磁勘探的影响不能忽略；采用正则化反演技术实现了同时考虑介质电阻率与磁导率的大地电磁二维正则化反演。主要取得如下认识：

(1)大于真空中磁导率的局部异常体对大地电磁观测存在明显的影响，二倍电阻率差异条件下、二倍于真空中磁导率的异常体足以改变卡尼亚视电阻率与相位形态；

(2)通过正则化反演可以实现电阻率与磁导率的反演，同时反演两个参数有利于提高反演效果；

(3)模型空间到反演空间的函数映射，将电阻率与磁导率限定在具有实际物理义的变化区间，提高反演的稳定性；

(4)高斯-牛顿法可实现同时考虑电阻率与磁导率的正则化目标函数优化，双共轭梯度稳定算法求解高斯-牛顿系统，求解过程稳定、计算高效。