常微分方程初值问题的一种改进Runge-Kutta方法
曾 光,陈朝敏,雷 莉,许 曦
(东华理工大学 理学院,江西 南昌 330013)
众所周知,许多科学与工程计算问题最终可归结为求解带初值问题的常微分方程,而Runge-Kutta方法是求解这类方程的重要方法之一。1895年,德国数学家C.D.T Runge发表了关于微分方程数值解法的经典论文,成为常微分方程初值问题Runge-Kutta方法的开山之作。最早的求解带初值问题的常微分方程的隐式Runge-Kutta方法是1824年由Chuchy给出的隐式Euler方法,1964年Butcher和Kuntzmann给出了对所有的正整数s都存在2s阶的隐式Runge-Kutta方法。此后有很多学者加入到这类问题的研究,在精度、计算效率、稳定性等方面Runge-Kutta方法都不断被改进(Ramos et a., 2007),Goeken 等(1999)考虑了自治方程,在计算级值时加入导数信息,在不增加函数计算次数的前提下提高了计算精度,得到了一类级阶Runge-Kutta方法。
在Kutta提出Runge-Kutta方法的一般格式中,系数的求解是通过Taylor展开式求得,其思想简单,易理解,不过其不足点是计算复杂度较高。在本文中,先通过第二类切比雪夫正交多项式构造了未知函数的级数展开式,然后运用高斯-洛巴托数值积分公式得到一种满足上述阶条件的改进Runge-Kutta法,并通过数值算例验证了改进Runge-Kutta方法是有效的算法,具有4阶精度。
1 改进Runge-Kutta算法构造
1.1 Runge-Kutta方法的阶条件
首先对阶条件进行讨论,为得到一般格式的Runge-Kutta方法的阶条件,奚梅成(2003)利用Taylor展开式比较同阶系数的方法,其思想易理解,不过计算比较繁琐。在本文中根据Butcher (2003)中给出的Butcher有根树理论,导出了Runge-Kutta方法的阶条件。
定义1 树t的阶ρ(t)和稠密度r(t)满足:
(1)ρ(τ)=γ(τ)=1;

n2ρ(t2)+…+nsρ(ts);

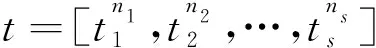
定义2 在Runge-Kutta的一般格式中,树集T上的函数Φi(x)定义如下:
式中,i=1,…,s,向量Φ(t)=(Φ1(t),Φ2(t),…,Φs(t))T称为树t的基本权。
下面给出一般Runge-Kutta阶条件:
定理1 一个Runge-Kutta方法是ρ阶的当且仅当下式
对于阶ρ(t)≤p的所有树t成立。
式中,b=(b1,…,bs)T,Φ(t)=(Φ1(t),Φ2(t),…,Φs(t))T.
(1)
则通过
可知,第二类Chebyshev多项式满足正交性,同时可得递推格式如下
U0(x)=1,U1(x)=2x,
Un+1(x)=2xUn(x)-Un-1(x).
第二类Chebyshev正交多项式还具有:奇偶性、有界性、完备性。
定理2若f(x)满足
(1)f(x)在区间(-1,1)为分段光滑的实值函数,
则函数f(x)在连续点x处可展成正交多项式的级数,即
=a0U0(x)+a1U1(x)+…,
(2)

1.2 算法构造
考虑常微分初值问题
(3)
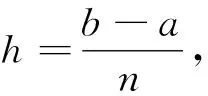
k=1,2,…,n.
则可把区间转移至[-1,1]中讨论,同时y(x)可用g(t)表示,将g(t)展成第二类Chebyshev多项式的级数形式,即

a2U2(t)+a3U3(t)+a4U4(t).
为计算级数展开式中的系数ai(x),结合高斯-洛巴托数值积分公式并化简可得
(5)

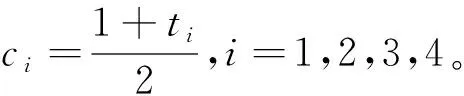

(6)
式中,F=(f(xk-1+c1h,g1),f(xk-1+c2h,g2),f(xk-1+c3h,g3),f(xk-1+c4h,g4))T,

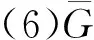
则有
hF=Qg0+DG
(7)
由于|D|≠0,则
G=hD-1F-D-1Qy(xk-1)
(8)
则由式(8)可构造出改进Runge-Kutta方法,它是四级隐式格式。即
(9)
最后给出改进Runge-Kutta算法步骤(宁德圣等,2016):
Step 1. 利用第二类Chebyshev多项式将未知函数展成正交多项式级数形式,得到式(2);
Step 2. 作区间变量代换,同时结合高斯-洛巴托数值积分公式可对展开式中系数进行数值求积,化简得到式(5);
Step 3. 由前两步可将原问题进行数值求解,整理可得到式(6)。由于初值g0=y(xk-1)已知,可将求解公式转化为式(8);
Step 4. 由此得到改进Runge-Kutta方法,具体格式为式(9)。
2 改进Runge-Kutta方法理论分析
这一部分主要对改进Runge-Kutta算法进行相容性、收敛性及精度分析,从理论上推导所构造的改进Runge-Kutta算法是可行、有效的算法。
2.1 相容性分析
定理3 改进的Runge-Kutta方法是相容算法。
证明 根据改进Runge-Kutta算法可制出对应的Butcher(图1)。

cAb0.268 60.324 9-0.190 70.150 8-0.016 40.50.436 70.022 20.061 1-0.020 00.806 30.417 00.207 60.212 9-0.031 210.444 50.111 00.444 500.444 50.111 00.444 50
则根据图1可知ci满足
则本文建立的改进Runge-Kutta方法满足相容性。
2.2 收敛性分析
由式(9)得到差分格式:
gk=gk-1+hφ(h,xk-1,gk-1),k=1,2,3,4
(10)
根据已得出的相容性分析,可以给出式(10)收敛性的充分性结论。
定理4 改进Runge-Kutta方法产生的差分格式(10)中,gk为常微分方程数值解,若φ(h,x,g)在Ω={(h,x,g)|a≤x≤b,g∈R}上关于g满足Lipschitz条件
|φ(h,x,g1)-φ(h,x,g2)|≤L|g1-g2|,
其中L>0为Lipschitz常数,则改进Runge-Kutta方法的数值解是收敛的(王泽文,2016)。
2.3 精度分析
改进Runge-Kutta方法的隐式方法,由于各级格式的复杂性,无法利用Taylor展开。结合有根树理论及Runge-Kutta方法的阶条件来判定方法的精度阶。
定理5 改进的Runge-Kutta方法的精度是4阶。
证明 由定义1可知,对于四阶树,可计算出各阶树的稠密度γ(t)及相对应的基本权Φ(t):
对于一阶树,若γ(t)=1,Φ(t)=b1+b2+b3+b4=1;
结合定理1,即对于的ρ(t)≤4的所有树满足
所以改进的Runge-Kutta方法精度为4阶。
3 数值算例
考虑如下初值问题:
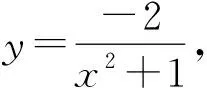

图2 精确解与改进Runge-Kutta方法的数值解Fig.2 Exact solution and numerical solution of improved Runge-Kutta method
通过图2可以看出,利用本文改进的方法在常微分数值解的精度方面可达到不错的效果,计算得到的数值解与精确解逼近效果很好。且与理论分析相一致,说明本文提供的改进算法应用于求解常微分初值问题的正确性和可行性。
4 结束语
研究了带初值问题的常微分方程数值解法,首先通过Butcher有根树理论得到一般Runge-Kutta方法的阶条件,利用广义傅里叶级数理论、第二类切比雪夫正交多项式及高斯-洛巴托求积公式构造了一种改进的Runge-Kutta方法,通过理论分析证明了所得方法满足相容性和收敛性,通过数值算例进一步验证了改进Runge-Kutta方法是有效的算法。

