基于EEMD和熵理论的电动汽车制动意图识别方法∗

王 波,唐先智,王连东,杨树军,马 雷

(燕山大学车辆与能源学院,秦皇岛 066004)

前言

电动汽车在制动过程中,会根据驾驶员的制动意图,调整再生制动和机械制动在制动过程中的使用比例[1-2]。因此对驾驶员制动意图识别的准确性会直接影响电动汽车再生制动的能量回收率。如何精准地识别驾驶员的制动意图是电动汽车再生制动技术急需解决的难题[3-4]。国内外一些学者都针对此问题进行了研究。在此前的研究中,主要是以制动踏板行程及其变化率等时域参量为识别参数,通过逻辑推断或模糊推理识别驾驶员的制动意图[5-8]。这种识别方法对于紧急制动和中等制动识别准确率较高。但对于平缓制动和中等制动而言,由于驾驶员对制动踏板的操作特征在时域中并不明显,如果直接在时域中以制动踏板行程及其变化率等识别参数对制动意图进行识别,则相近意图不易区分。由于制动踏板行程变化率的时域信号容易受到测量误差的干扰,引入的这一参数不但没有提高识别精度,反而会降低识别准确率[9-12]。因此作者在之前的研究中,将制动意图识别引入频域,运用经验模态分解(EMD)将识别信号分解,并进行Hilbert变换,运用Hilbert局部边际能量谱提取信号的特征向量,并进行聚类识别,以进一步提高制动意图的识别准确率。该方法经试验证明,可以提高识别的准确率,但是制动踏板信号中会存在间歇性成分或脉冲成分,普通的EMD算法会受这些成分的影响使信号极值点产生偏差,之后的包络拟合也会随之产生偏差,易发生模式混叠[13-15]。如发生模式混叠,信号在进行EMD后,相同频率的成分会被分配到多个固有模态函数(IMF)中,或者在一个IMF中包含多个分量的成分。这样会改变每个IMF的局部特征能量,从而使提取的特征向量产生误差,导致初始聚类中心产生偏差,阻碍了识别准确率的进一步提高。

于是本文中采用平均经验模式分解(EEMD)算法,抑制制动踏板信号的模式混叠现象,用样本熵提取信号的特征,最后采取聚类算法进一步提高制动意图的识别准确率。

1 EEMD算法

为抑制制动踏板信号在经验模态分解(EMD)过程中的模式混叠现象,向制动踏板信号中加入频率均匀分布的噪声,使制动踏板信号中的间断成分变为连续。由于噪声幅值的统计均值为零,因此其幅值可相互抵消,使其不会对制动信号造成影响,同时可有效抑制模式混叠现象。

1.1 EMD原理与算法[14-15]

对初始信号X(t)所有的极大值点和极小值点进行三次样条插值,拟合出上、下包络线Xmax(t)和Xmin(t),取均值m1(t)为

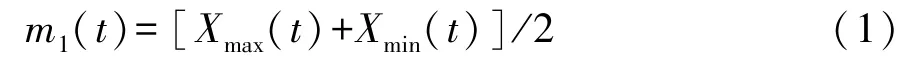
从原始信号中减去平均包络得到h1(t):

h1(t)如果不满足固有模态函数的条件,则成为新的初始信号,重复之前的步骤得

式中m11(t)为h1(t)的包络线均值。若h11(t)仍不满足固有模态函数的条件,则重复以上步骤,迭代k次得

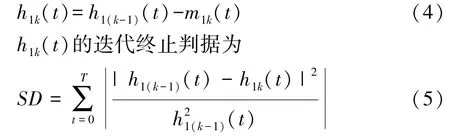
式中SD为迭代结果的标准差,其取值范围为0.2～0.3。

若h1k(t)满足迭代终止的要求,则h1k(t)为1阶固有模态函数,用c1(t)表示。用信号X(t)初值减去1阶固有模态函数得到信号残差r1(t),即

r1(t)为新的初始信号,重复EMD过程,可得全部信号残差ri(t),即

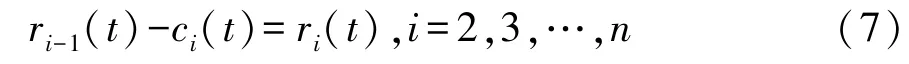
显然,初始信号X(t)可由n阶IMF和残差rn(t)组成,即

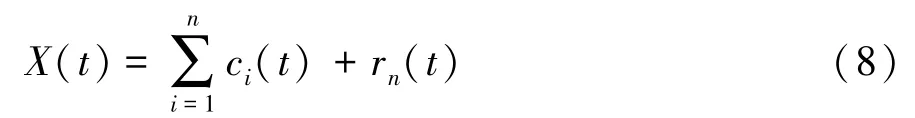
1.2 EEMD算法[16-17]

将白噪声nm(t)加入到制动踏板信号X(t)中,得到新的初始信号Xm(t),即

式中m为EMD分解次数。

运用EMD算法对新的初始信号Xm(t)分解,得到Xm(t)的IMF分量cm,j。cm,j为第m次EMD分解后,信号的第j个IMF分量。若1≤m≤M,通过以上算法可得M组IMF序列{cm,j}。将M组{cm,j}的平均值作为EEMD算法的第j个IMF分量,即

为证明EEMD算法对模式混叠的抑制作用,将正弦信号加入带有间歇性成分白噪声,如图1所示,并进行EMD和EEMD分解,见图2～图4。对比图2中的分量3和图4中的分量5,可以看出EMD分解产生了模式混叠现象,分量3已经部分失真。EEMD分解可抑制模式混叠,如图4所示,分量5很好地体现了原正弦信号的特征。

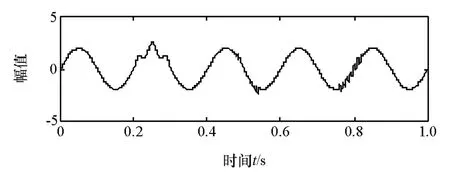
图1 加入白噪声的正弦信号

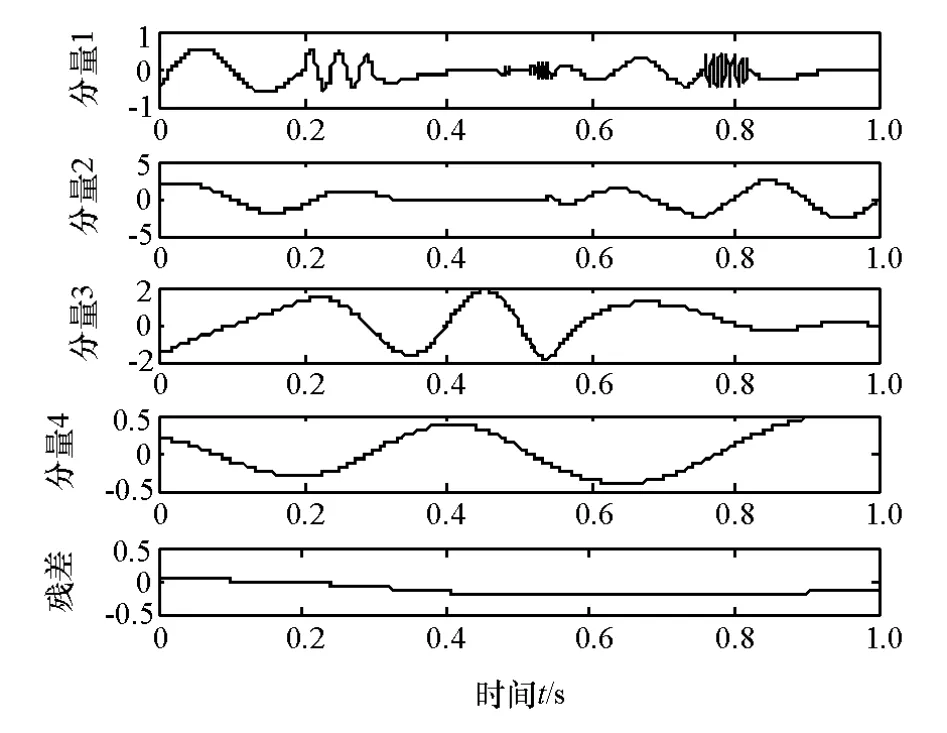
图2 EMD分解结果

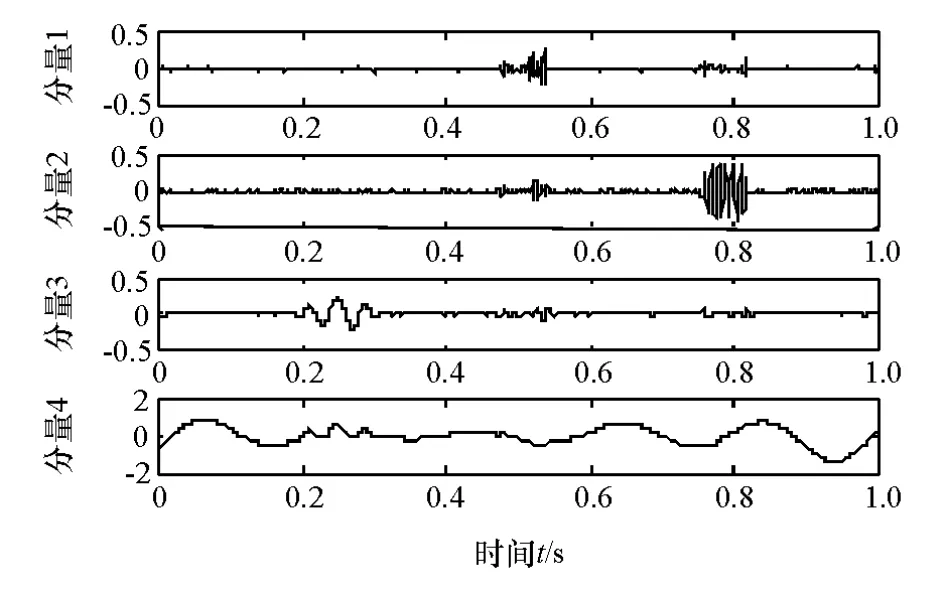
图3 EEMD分解结果(分量1-4)

图5和图6分别为中等制动和平缓制动踏板信号,现采用平均经验模式分解(EEMD)。将踏板信号分解为多个IMF,分别如图7和图8所示,以便于信号特征的提取。

2 基于样本熵的IMF特征提取

2.1 样本熵的基本原理

样本熵体现了信号时间序列的复杂程度,信号时间序列越复杂,它的样本熵值越大；信号时间序列越简单,它的样本熵值越小。本文中运用样本熵对制动踏板信号的特征进行提取,即计算各IMF分量的样本熵,得到其特征向量。

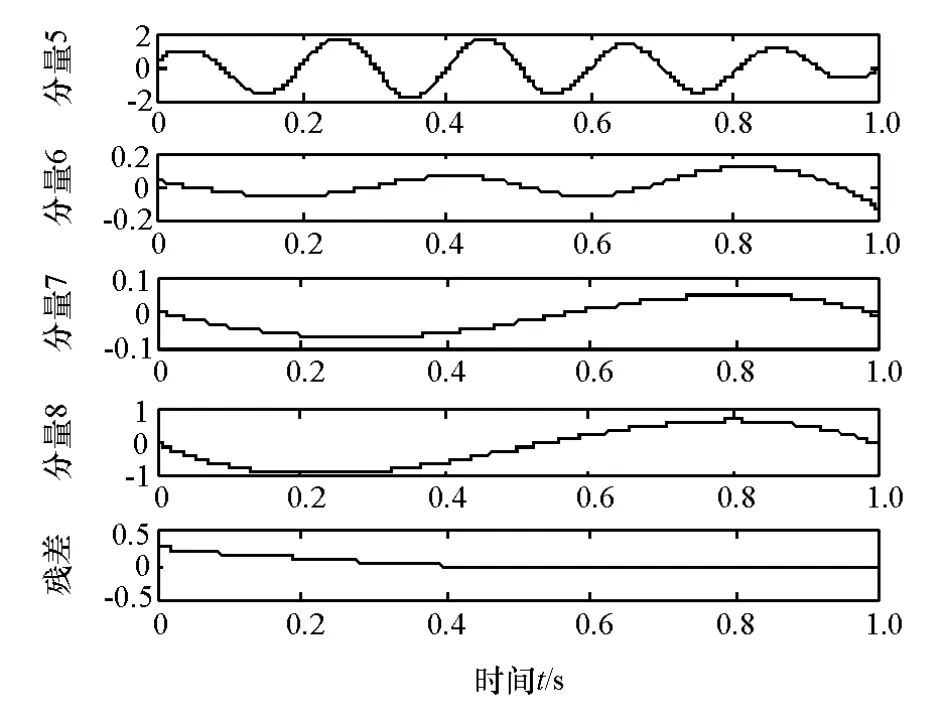
图4 EEMD分解结果(分量5-8)

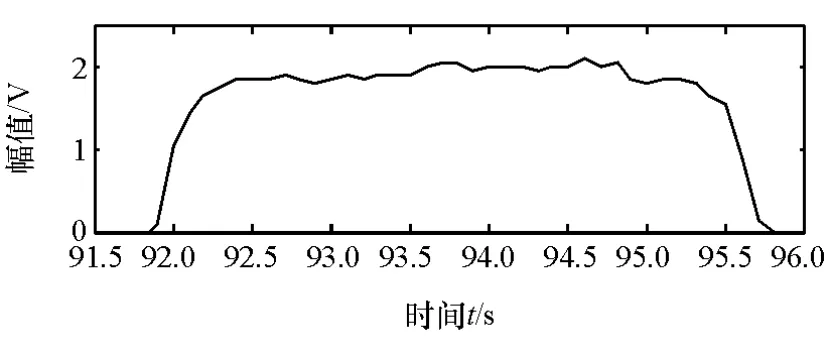
图5 中等制动踏板信号

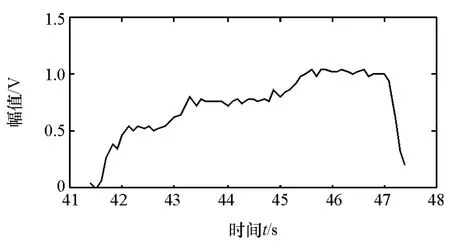
图6 平缓制动踏板信号

样本熵的计算方法如下[18-19]。

(1)构造m维矢量X(i)

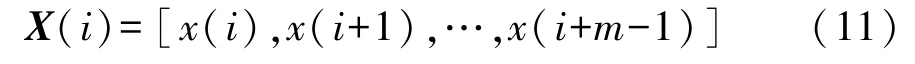
式中 i＝1,…,N-m+1。

(2)计算X(x)与X(j)的距离d[X(i),X(j)]

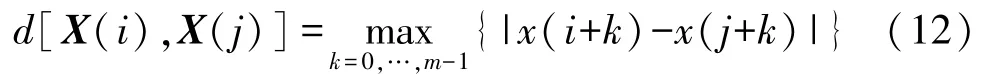
(3)X(x)与X(j)的距离d[X(i),X(j)]小于r的数目用Num{d[X(i),X(j)]＜r}表示,其与N-m的比值,用(r)表示,即

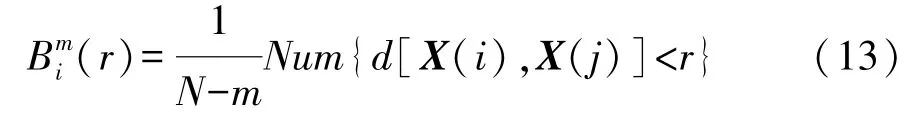
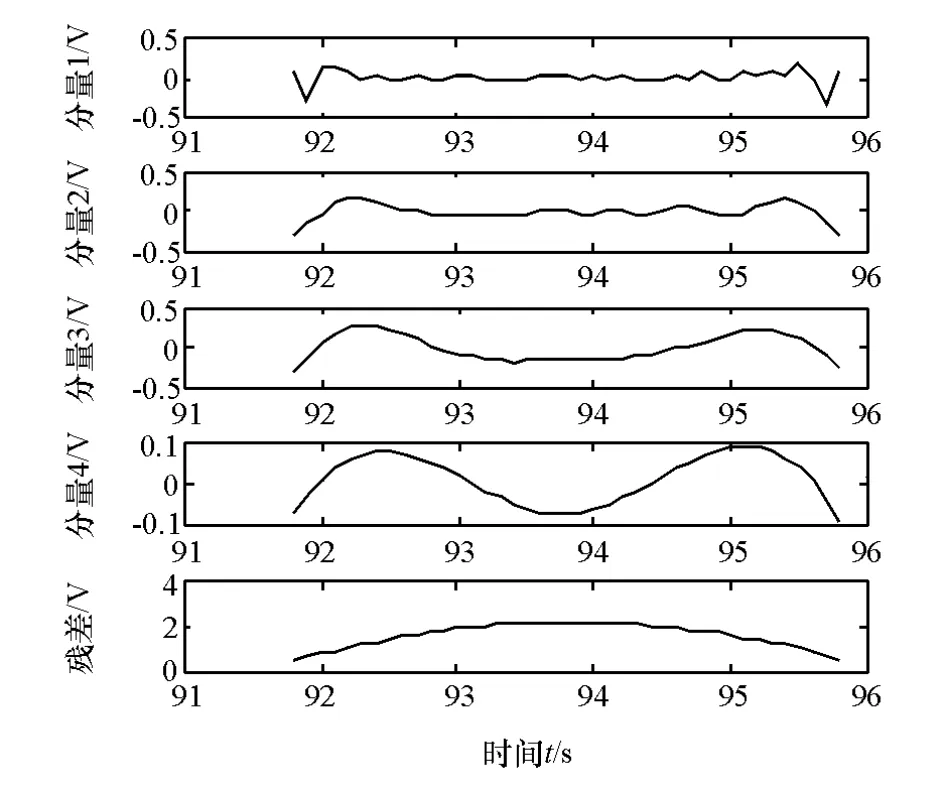
图7 中等制动踏板信号EEMD分解结果

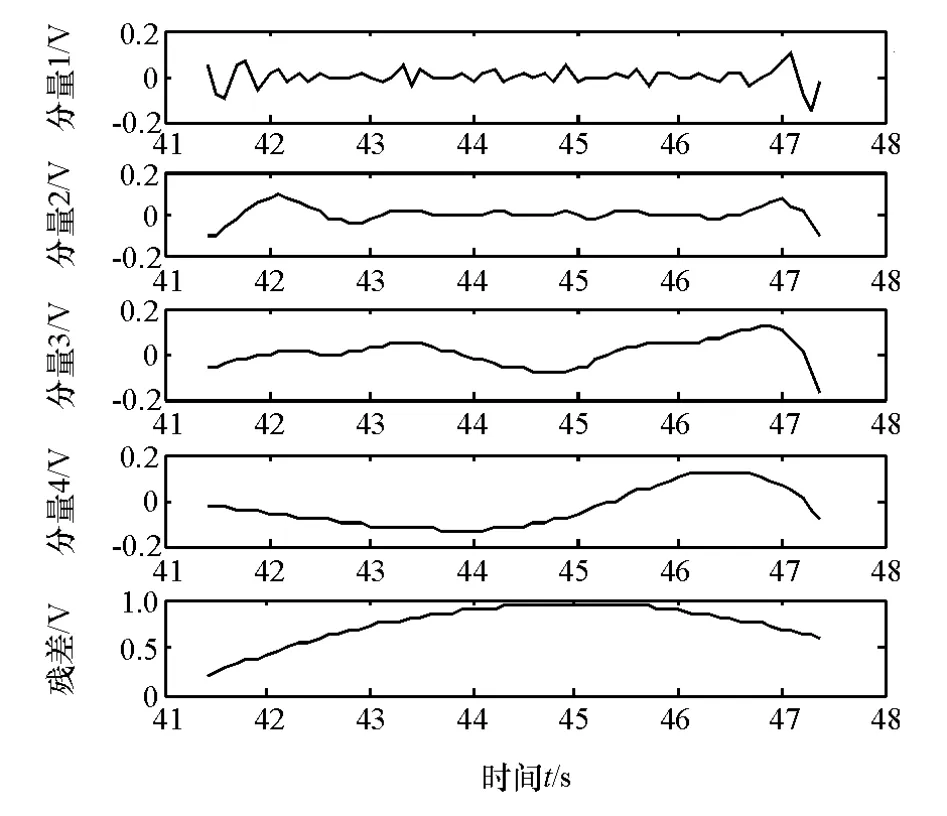
图8 平缓制动踏板信号EEMD分解结果

式中 i,j＝1,…,N-m+1,i≠j。

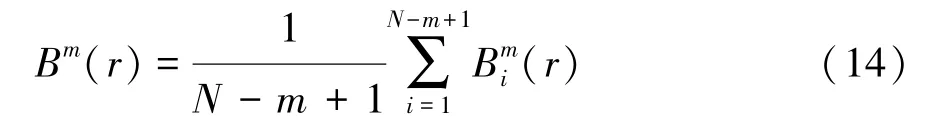
(4)将矢量维数增加1得到m+1维矢量,重复以上步骤得到

提取如图5和图6所示的中等制动和平缓制动信号的特征。求中等制动和平缓制动信号的IMF分量(图7和图8)的样本熵,分别如图9和图10所示。

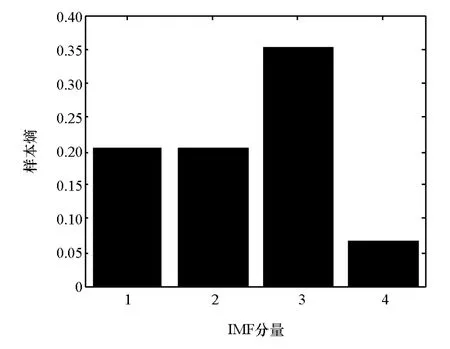
图9 中等制动IMF分量的样本熵

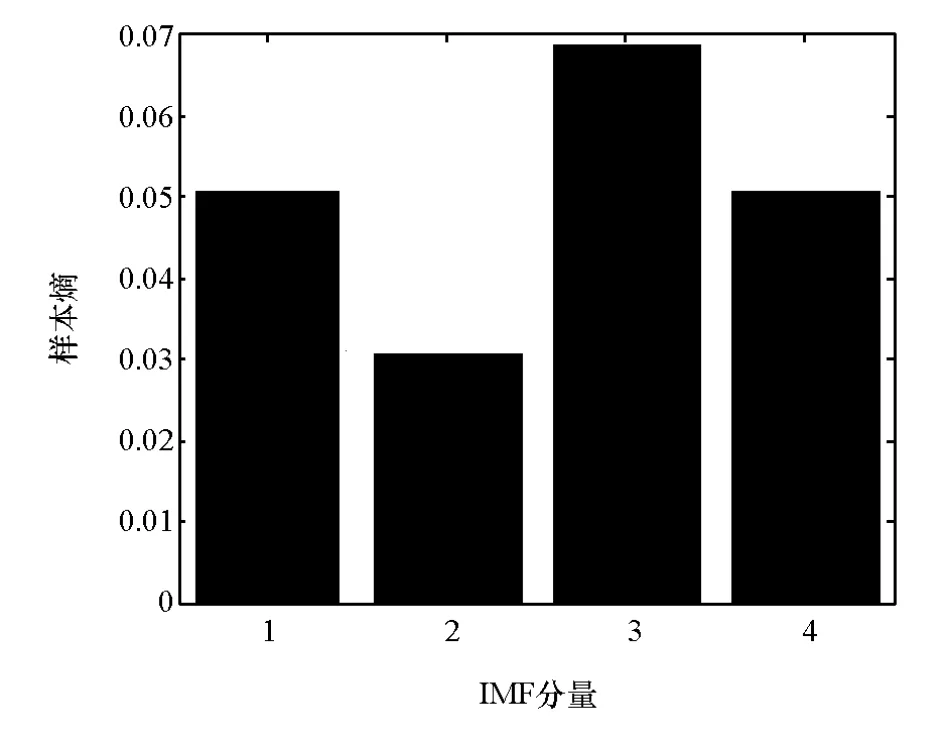
图10 平缓制动IMF分量的样本熵

2.2 IMF分量特征筛选

EEMD将制动踏板信号进行分解后可得到许多IMF分量,若对所有IMF分量求其样本熵,则计算量过大,信号识别的效率低下。因此须将IMF分量进行筛选,选择承载信息较丰富的IMF分量求其样本熵,提取信号特征。本文中用Shannon熵对IMF分量进行筛选。

设{ci}为经EEMD分解后信号的IMF分量,其中1≤i≤n。计算各IMF分量的Shannon熵H(ci):

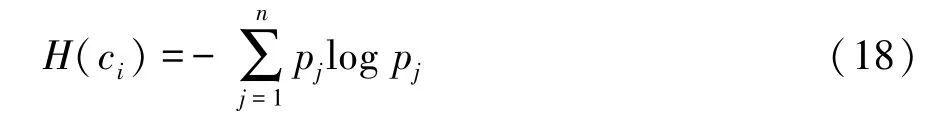
式中:pj为信号IMF分量{ci}第j个元素取值的概率。

设定门限值 γ(各 IMF分量 Shannon熵的均值),若某IMF分量的Shannon熵大于γ,表明该IMF分量带有信号中的有用信息,特征明显,其样本熵可作为踏板信号的特征值；若IMF分量的Shannon熵H(ci)小于γ,表明该IMF分量带有信息较少,应舍弃[20-21]。

图11和图12分别为中等制动和平缓制动的踏板信号IMF分量Shannon熵。图中水平直线为踏板信号IMF分量的Shannon熵的门限值γ。可见中等制动信号和平缓制动信号的第3个和第4个IMF分量的Shannon熵大于门限值,说明第3个和第4个IMF分量带有丰富的信息,可用作特征提取,因此采用制动踏板信号的第3个和第4个IMF分量的样本熵作为信号特征向量的特征值。

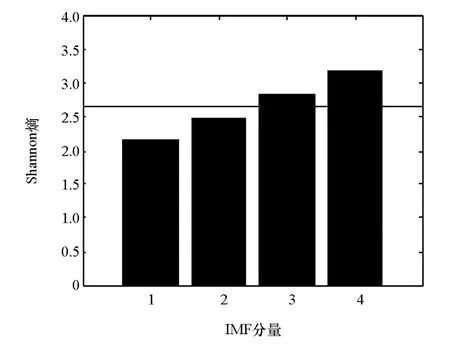
图11 中等制动踏板信号IMF分量Shannon熵

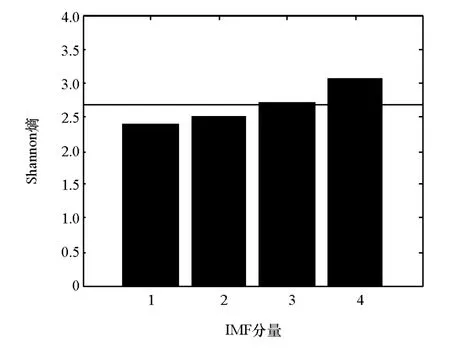
图12 平缓制动踏板信号IMF分量Shannon熵

3 聚类识别

采用K-均值聚类算法对提取到的制动踏板信号特征向量进行制动意图的聚类识别。该算法的步骤如下[22-23]。

(1)对于有k个聚类中心mj(j＝1,2,…,k)的数据集X＝{x1,x2,…,xn},计算数据集中每个元素与各聚类中心的距离d(xi,mj),其中i＝1,2,…,n,j＝1,2,…,k,找到距离每个元素最近的聚类中心d(xi,mj)＝min{d(xi,mj),j＝1,2,…,k},并将每个元素归到该聚类中心,即此时xi∈mj。

(2)计算新的聚类中心

如果J收敛则停止迭代,否则转到步骤(1)继续迭代。

4 试验验证

4.1 离线验证

选择10组制动踏板行程数据,其中中等制动和平缓制动各半。根据前面提出的EEMD算法,将每组数据都采用EEMD分解出4个IMF分量。选取两个Shannon熵最大的IMF分量的样本熵值作为制动踏板信号的特征向量。10组数据的特征向量如表1所示。其中序号1,2,5,7,9的特征向量为平缓制动的制动踏板行程信号的特征向量。序号3,4,6,8,10的特征向量为中等制动的制动踏板行程信号的特征向量。

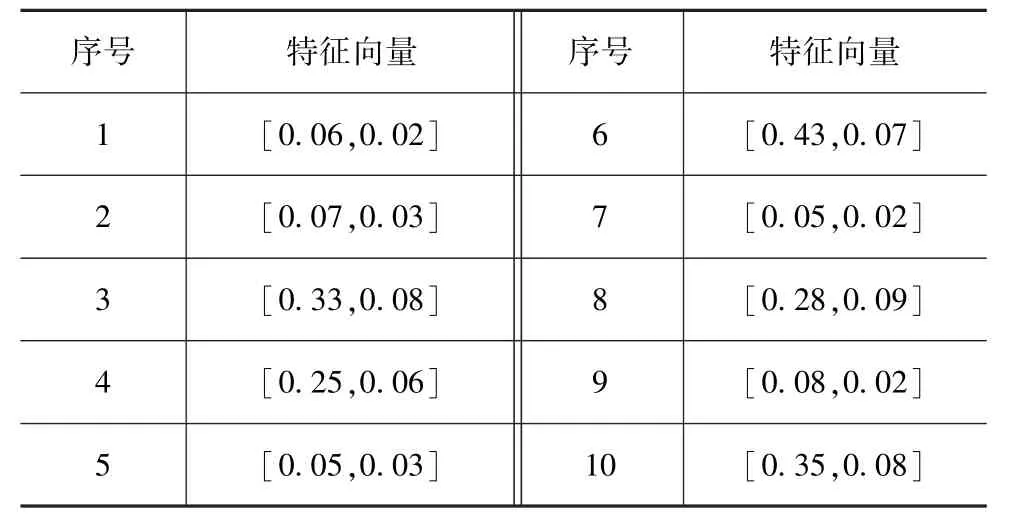
表1 制动踏板信号特征向量

图13为采用聚类识别算法对10组特征向量进行识别的结果。从图中明显可以看出,聚类识别算法把特征向量分成两类,分别用圆圈和三角表示,五角星为聚类算法的聚类中心。序号1-10的特征向量分类结果如向量[2；2；1；1；2；1；2；1；2；1]所示,其中2代表平缓制动,1代表中等制动。可见识别结果完全正确,与基于EMD分解的HHT制动意图识别算法相比,识别准确率提高10%(基于HHT的制动意图识别算法识别准确率为90%,见文献[13])。由此可以验证,通过EEMD将制动踏板信号分解为IMF分量,选择Shannon熵较大的IMF分量,通过计算其样本熵提取制动踏板信号特征,并进行聚类识别,此方法可以很好地抑制模式混叠,在离线情况下能更好地提取不同制动意图下制动踏板信号特征,并准确识别驾驶员的制动意图。

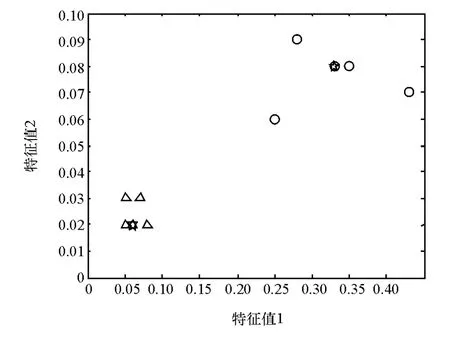
图13 聚类识别结果

4.2 实时验证

实时验证采用的试验用车为某品牌皮卡车。采用dSPACE/MicroAutoBox进行数据在线采集和制动意图识别。在试验中,驾驶员按照要求进行制动操作,进行了10次制动。制动踏板信号通过安装自制的制动踏板行程信号采集装置进行采集,如图14所示。

图14 制动踏板行程信号采集装置

图15为实时采集的制动踏板行程信号。其中,1,2,5,6制动为平缓制动；3,4,7,8,9,10制动为中等制动。图16为基于EEMD和熵理论的制动意图聚类识别方法与基于HHT的制动意图识别方法对制动意图的在线识别结果对比。基于EEMD和熵理论的制动意图聚类识别法的识别结果用米星表示,基于HHT的制动意图识别法的识别结果用圆圈表示,其中识别结果1.5代表平缓制动,2代表中等制动。从识别结果可以看出,两种识别方法只有在编号为8的制动意图识别结果上产生了分歧。基于HHT的制动意图识别方法将编号为8的制动意图识别为平缓制动,识别结果错误。基于EEMD和熵理论的制动意图聚类识别方法对驾驶意图的识别结果全部正确。

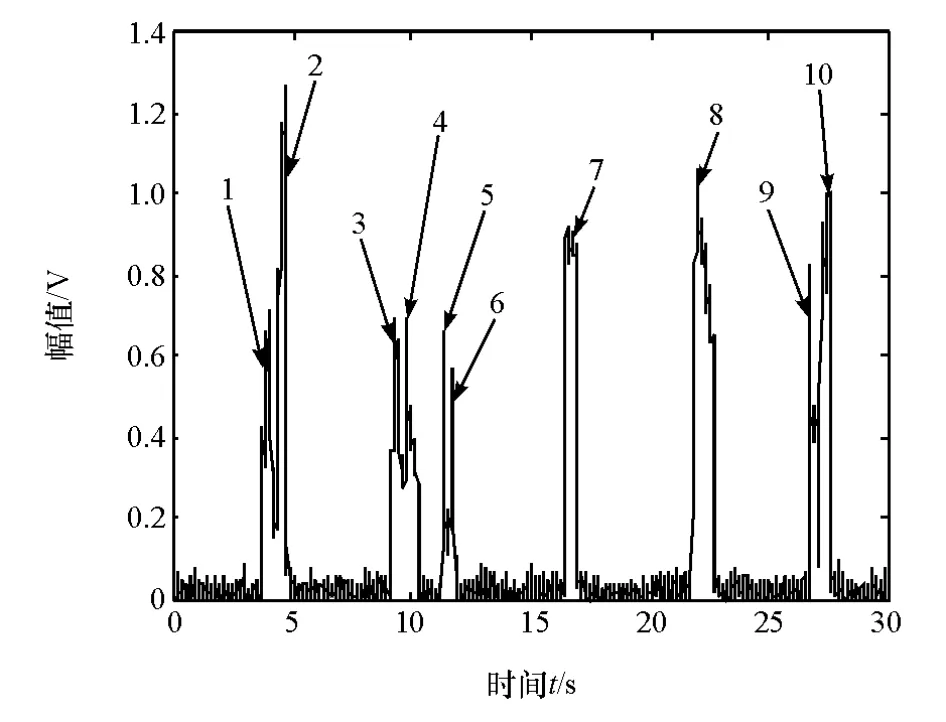
图15 制动踏板行程实时信号

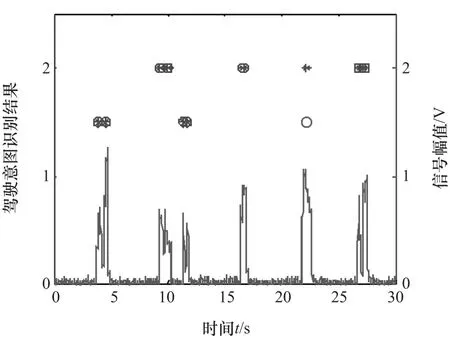
图16 制动意图的在线识别结果

图17为基于EEMD和熵理论的制动意图聚类识别方法与基于HHT的制动意图识别方法所需识别时间的对比情况。由图17可看出,进入制动工况(即踩下制动踏板)的时刻x1＝3.67s,基于EEMD和熵理论的制动意图聚类识别方法识别出平缓制动意图的时刻x2＝3.94s,识别时间为0.27s。基于HHT的制动意图识别方法识别出平缓制动意图的时刻x3＝4.04s,识别时间为0.37s。可见,本文中提出的制动意图识别方法较基于HHT的制动意图识别方法响应速度快了0.1s。

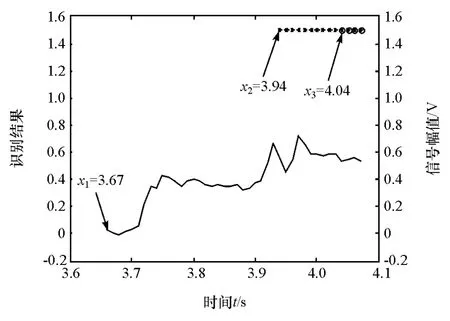
图17 制动意图在线识别响应时间

5 结论

(1)EEMD相比于文献[13]中所应用的EMD算法,在制动踏板信号分解和信息挖掘的过程中,减小了制动踏板信号中由于间歇性成分或脉冲成分造成的模式混叠现象,使分解得到的IMF分量具有更准确的特征。离线试验的结果表明,本算法的识别准确率比基于HHT的制动意图识别算法提高了10个百分点。

(2)运用熵理论提取IMF分量特征相比于文献[13]所用的Hilbert局部边际能量谱提取信号的特征,减少了有效IMF的数量,降低了特征向量的维数,提高了计算效率。实时试验结果表明,该算法可准确地对驾驶员的制动意图进行实时在线识别,比基于HHT的制动意图识别法的响应时间缩短了0.1s,具有更好的实时性。