考虑冲压工艺约束的车身骨架断面形状优化∗

桂春阳,鞠 伟,左文杰

(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022； 2.吉林大学机械科学与工程学院,长春 130022；3.中国第一汽车股份有限公司技术中心,长春 130011)

前言

在汽车概念设计阶段,车身经常简化为由复杂断面薄壁梁搭建而成的简化模型[1-2],计算其刚度特性[3],同时提供车身质量和转动惯量评价指标[4]。_薄壁梁是一种轻量化结构,由金属薄板冲压焊接装配而成,具有刚度-质量比高的优点[5]。断面形状决定了薄壁梁的力学特性(横截面积、弯曲惯性矩、扭转惯性矩等),进而影响车身的整体性能。因此,在汽车的概念设计阶段,薄壁梁断面的力学特性求解对于车身设计非常重要[6]。

一方面,丰田公司最早开始了断面设计与分析的研究,并提出了车身设计的FOA方法[7]。采用该方法,工程师可快速地选择最佳的断面形状,但该方法只能计算开口和单室断面形状,不能求解车身结构中常见的双室、三室和四室断面。

另一方面,在断面求解的基础上,需要寻找断面积最小、弯曲惯性矩与扭转惯性矩最大的断面形状,这是个优化设计问题[8]。当前,大多依靠经验和现有断面数据库来调整断面形状,人工实现断面形状的优化设计。目前,这方面的工作大多关注于断面形状的拓扑优化[9],但未考虑金属薄板的冲压工艺约束,以致于金属薄板很难或根本不可能制造出来[10]。Yoshimura等[11]提出了车身断面形状设计和优化方法,但也只能优化开口、单室与双室断面,依然不能求解三室和四室断面,更不能对这些复杂断面进行优化设计。

因此,本文中会推导车身骨架常用的开口、单室、双室、三室和四室的断面力学特性求解公式。全面考虑冲压工艺约束,包括最短线段约束、拔模角约束、倒圆角半径约束,在断面弯曲惯性矩和扭转惯性矩的约束下,对断面形状进行优化设计,寻求最小断面面积,以达到车身薄壁梁轻量化设计的目的。

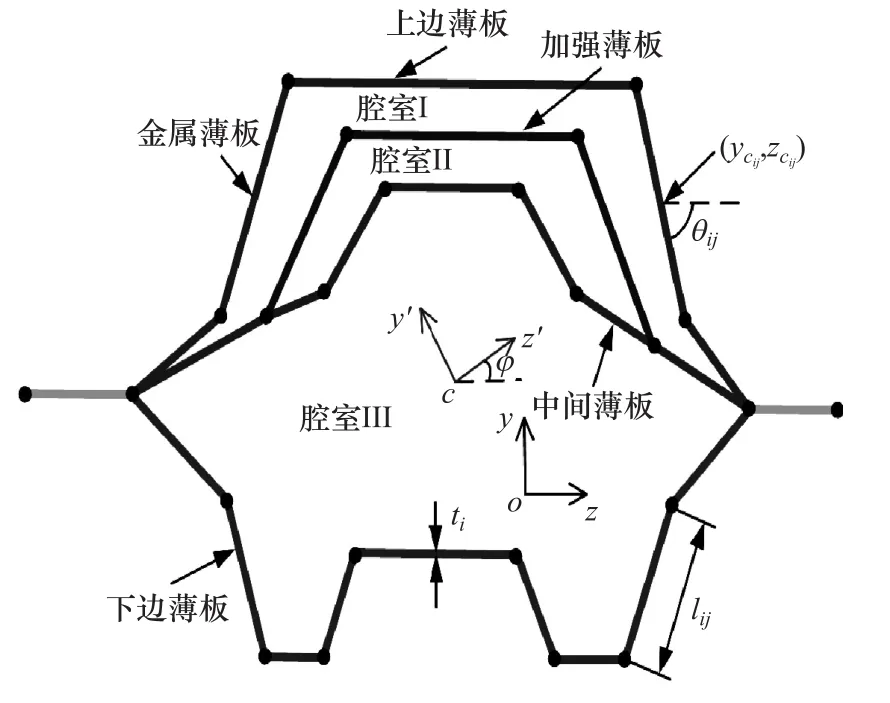
图1 一种典型的断面形状

1 复杂断面力学特性求解

一个典型的断面形状如图1所示,其中yoz坐标系为断面的设计坐标系,c点为断面的形心,每片金属薄板可视为由矩形片段组成的折线,因此,断面面积为

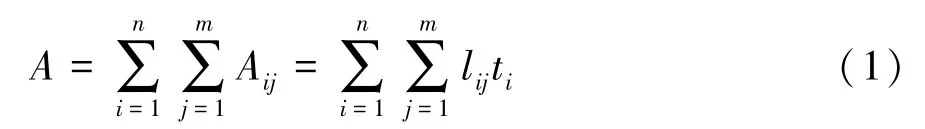
式中:n为薄板数量；m为第i片金属薄板的片段数量；lij和Aij分别为第i片金属薄板的第j个片段的长度和面积；ti为第i片薄板的厚度。

断面的形心坐标为

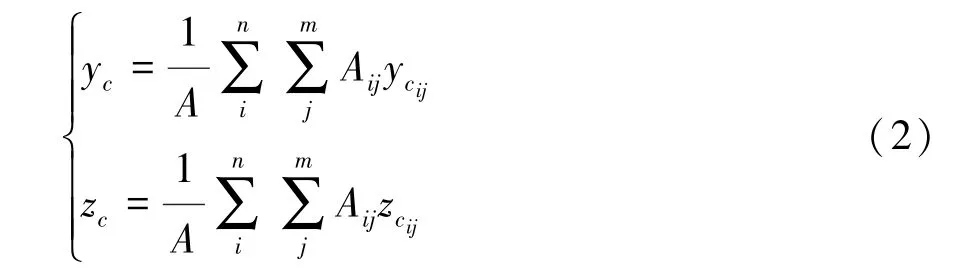
关于断面形心的弯曲惯性矩Iy,Iz和惯性积Iyz分别为

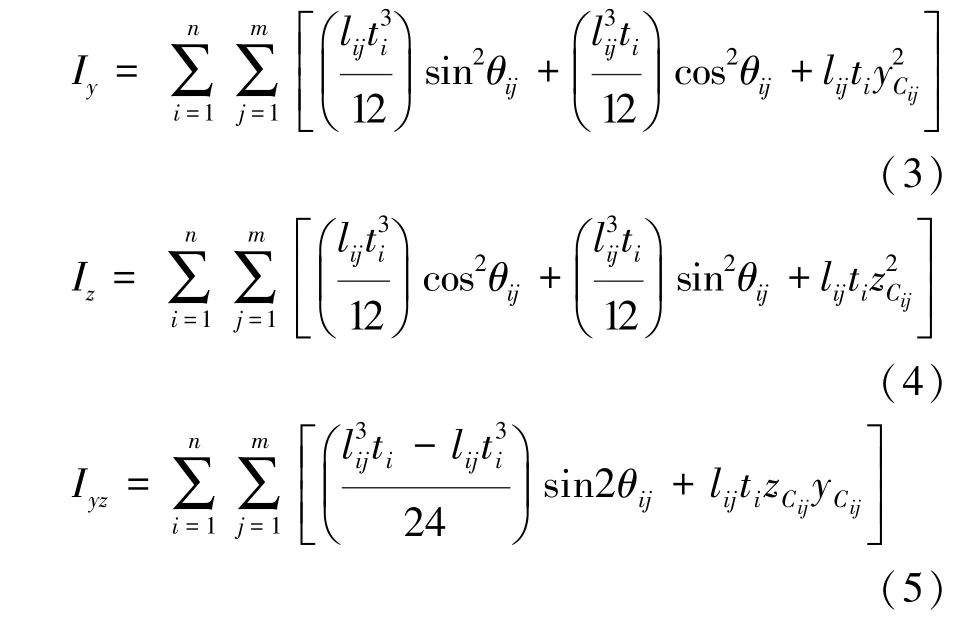
式中θij为第i片金属薄板的第j个片段与z轴的夹角,如图1所示。

由Iy,Iz和Iyz得到断面主惯性矩为

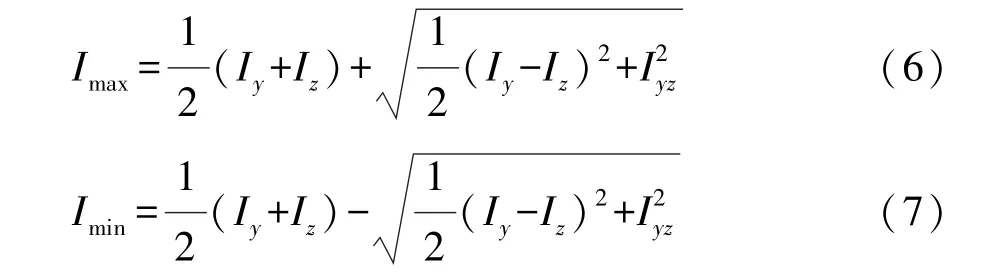
主惯性坐标系y′cz′与绘图坐标系yoz之间的夹角φ为

计算扭转惯性矩取决于断面的类型。开口断面的扭转惯性矩为

单室断面如图2所示,其扭转惯性矩为

图3为双室断面,其扭转惯性矩为

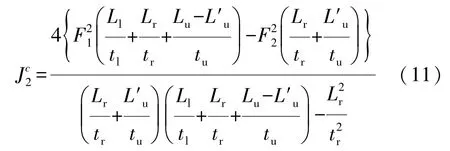
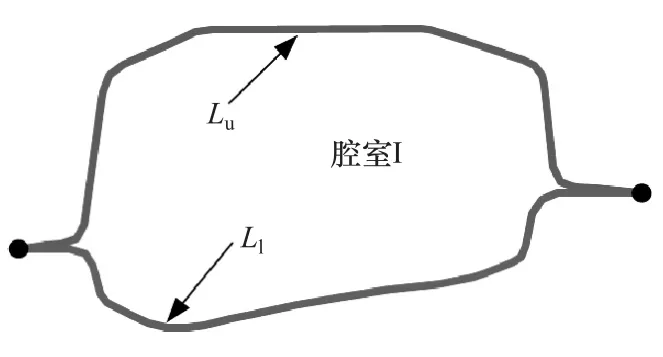
图2 单室断面

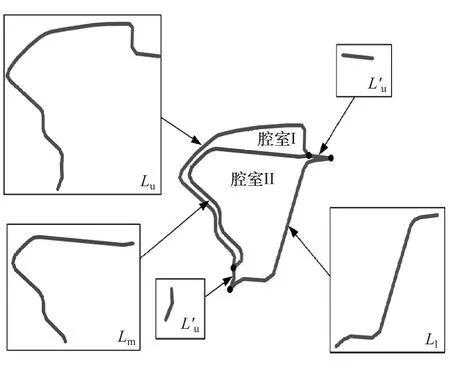
图3 双室断面

图4为三室断面,其扭转惯性矩为

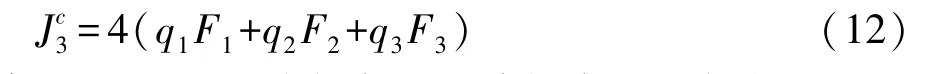
式中q1,q2和q3需由式(13)线性方程组解得。

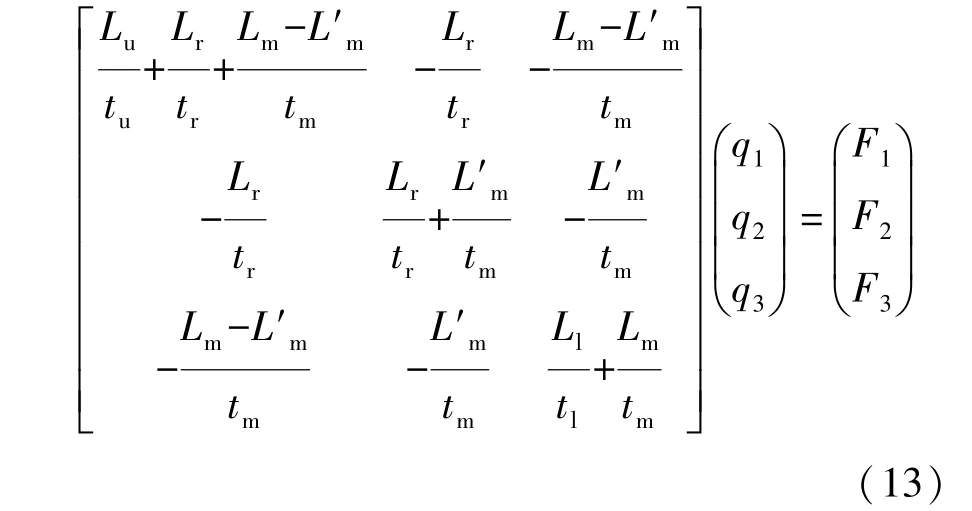
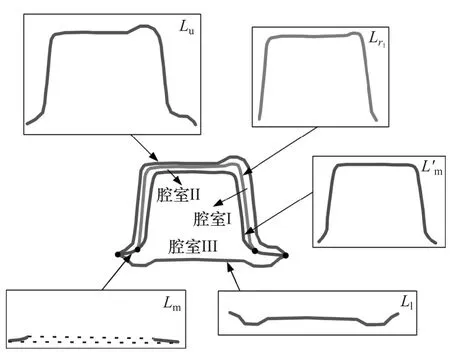
图4 三室断面

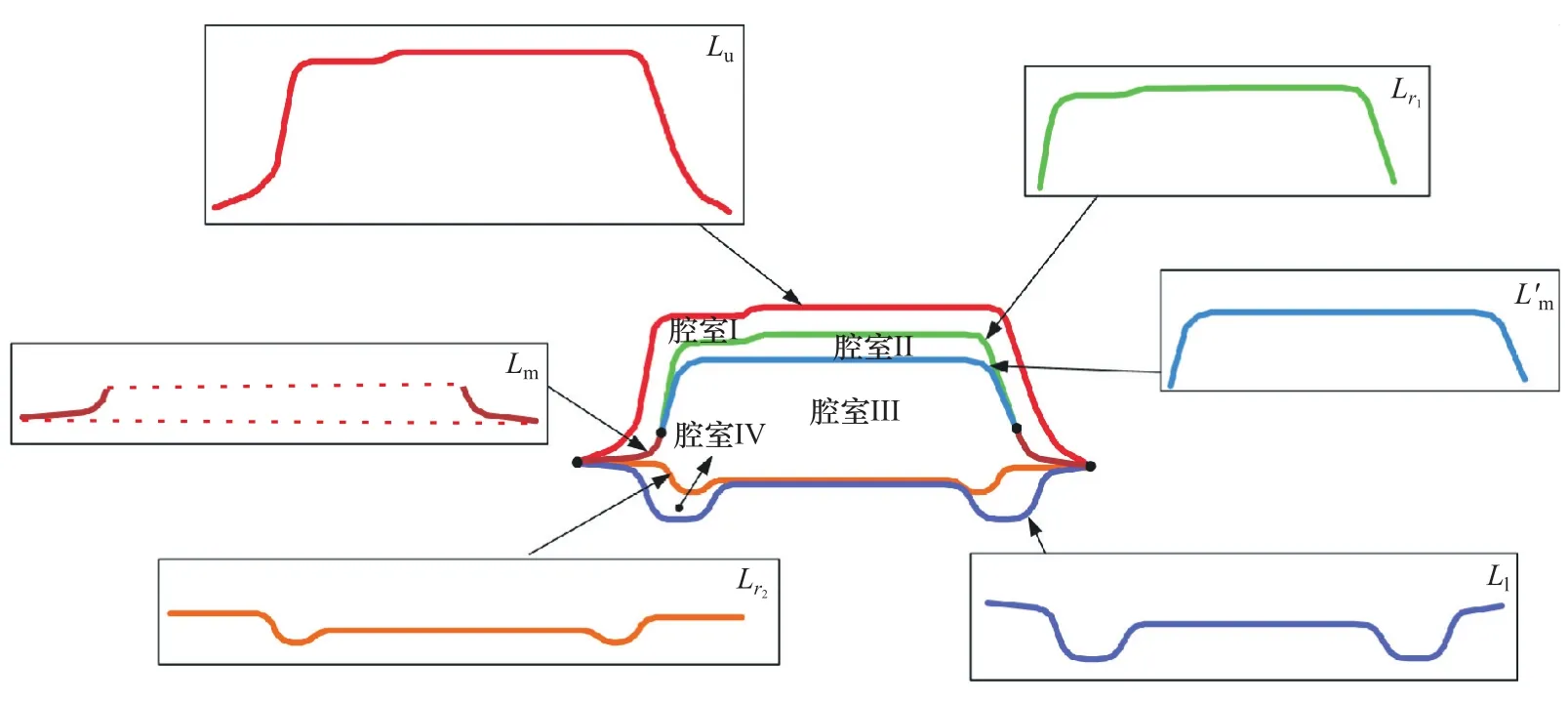
图5 四室断面

图5为四室断面,其扭转惯性矩为

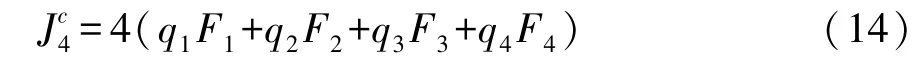
式中q1,q2,q3和q4需由式(15)线性方程组解得。

在式(13)和式(15)中,F1,F2,F3和F4分别为腔室Ⅰ、腔室Ⅱ、腔室Ⅲ和腔室Ⅳ的封闭面积；Lu,Ll,Lm,Lr1和Lr2分别为上边薄板、下边薄板、中间薄板、加强薄板1和加强薄板2的长度；Lu′为上边薄板的一部分的长度,如图3所示；Lm′为中间薄板的一部分,同时也是腔室Ⅱ和腔室Ⅲ的公共部分的长度,如图4和图5所示；tu,tl,tm,tr1和tr2分别为上边薄板、下边薄板、中间薄板、加强薄板1和加强薄板2的厚度。

当一个复杂断面带有翻边,即由开口和闭口断面共同组成时,扭转惯性矩J可表示为

式中k表示断面腔室的数量。

总之,断面的弯曲惯性矩Iy,Iz和惯性积Iyz的计算公式与断面形状无关；而扭转惯性矩J的计算公式与断面腔室的数量相关。

2 冲压工艺约束

车身钣金件主要由冲压成型,基本的冲压工艺约束包括:最短线段约束、拔模角约束、倒圆角半径约束和装配约束。

2.1 最短线段约束

如果断面的直线段太短,则无法冲压制造出来,如图6所示。因此,线段长度需满足如下条件:

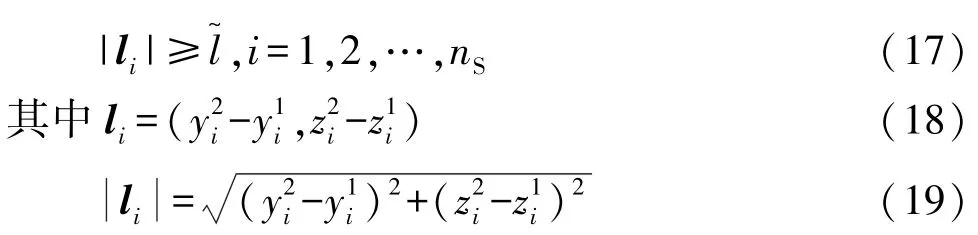
式中:nS为线段的数量；为线段允许的最小长度；li为第i个线段的向量表达式；()和()分别为矩形片段两个端点的坐标；｜li｜为向量li的长度(模)。

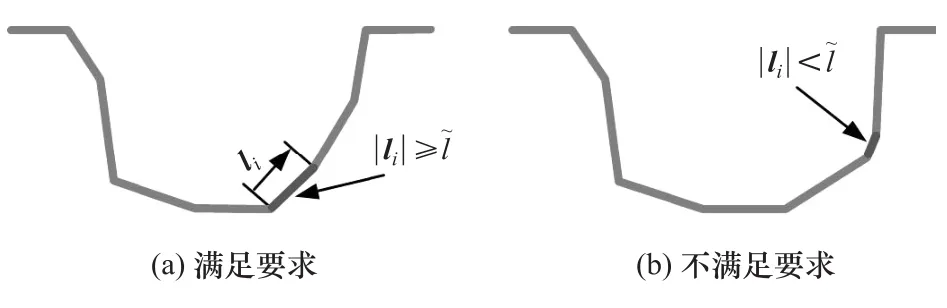
图6 最小线段长度约束

2.2 拔模角约束

拔模角是断面线段的方向向量与冲压方向的夹角,如图7所示。如果拔模角小于允许的角度,凸模则无法从凹模中拔出。因此,拔模角需满足以下条件:

式中:nd为拔模角的数量；α～为允许的最小拔模角度；αi为断面的第i个拔模角度。

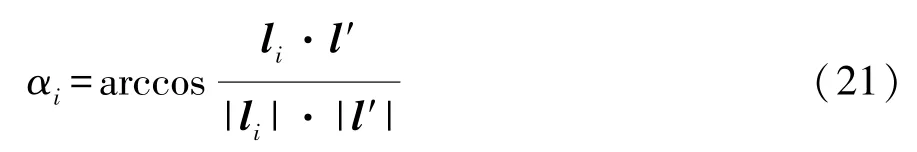
式中l′为翻边的方向向量,如图7所示,其公式可以表示为 l′＝(),｜l′｜为向量 l′的长度。

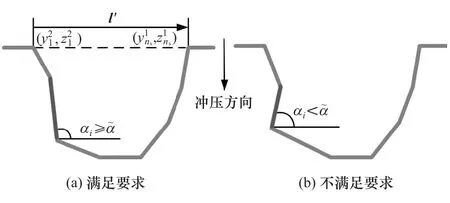
图7 拔模角约束

2.3 倒圆角半径约束

倒圆角半径是指薄板的弯曲半径,如图8所示。如果倒圆角半径小于允许值,凸模将无法制造出来或是凸模的刚度、强度等指标不足。因此,倒圆角半径需满足以下条件:

式中:nC为倒圆角的数量；R～为允许的最小倒圆角半径；Ri为第i个倒圆角半径。

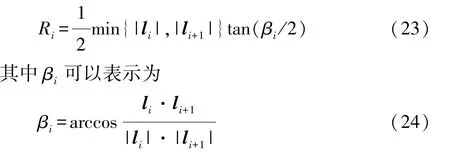
图8 倒圆角半径约束

2.4 装配约束

在冲压约束过程中,不允许薄板有交叉,如图9所示。当冲压约束的交叉点数量nisp为0时,装配约束满足要求,因此装配约束必须满足以下条件:

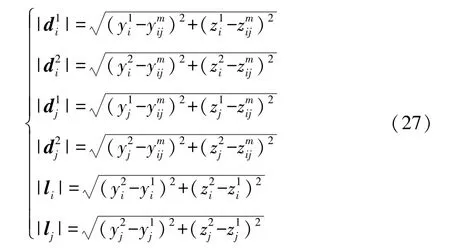
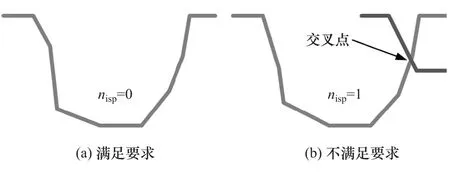
图9 装配约束

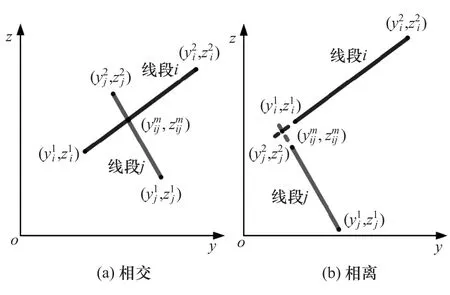
图10 线段相交与分离

3 断面形状优化

弯曲惯性矩Iy,Iz和扭转惯性矩J是评价薄壁梁力学特性的基本指标。因此,在满足这些指标和冲压工艺约束的前提下,优化断面形状,使断面面积最小,从而实现薄壁梁的轻量化目的。断面由可移动和固定的控制点来决定其形状,如图1所示。在断面形状优化过程中,由于造型或车身空间布局的要求,固定控制点不可移动,也即不作为优化的设计变量。

薄壁梁断面形状优化问题可为

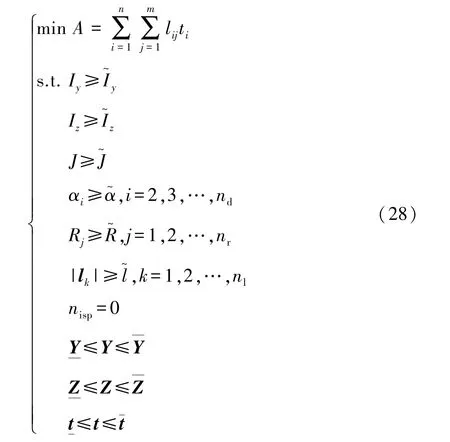
由于式(22)和式(25)是关于坐标变量的离散函数,无法求其解析灵敏度信息,所以不能采用梯度类优化算法求解。因此,只能采用不依赖梯度信息的生物进化算法求解,本文中采用遗传算法来优化式(28)的高度非线性优化问题。采用罚函数法将式(28)的约束全部施加到目标函数上,将约束优化问题转化为无约束优化问题,从而可采用遗传算法的适应度函数来评价该目标函数。

针对以上方法,自主开发了断面设计和优化软件SuperSection[12],软件界面见图11,可以设计任意形状和任意腔室数量的断面并进行断面力学特性求解与形状优化。图12为软件断面形状优化界面。

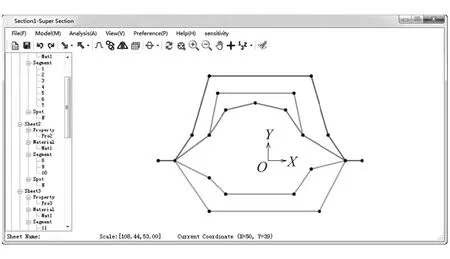
图11 SuperSection软件界面图

4 断面形状优化算例

带有翻边的四室断面非常复杂,常应用于汽车车身B柱下端,如图13所示。该断面的坐标变量和板厚变量分别列入表1和表2。为满足设计要求,点2,7,11和14为固定约束,其余点的坐标全部为设计变量,但只能在图13中的矩形框内移动。本次优化过程共迭代80次,遗传算法每一代的种群数量为30,交叉概率为0.55、变异概率为0.20、精英保留概率为0.01。本次优化采用普通计算机(Xeon E3 CPU,内存8G)进行计算。

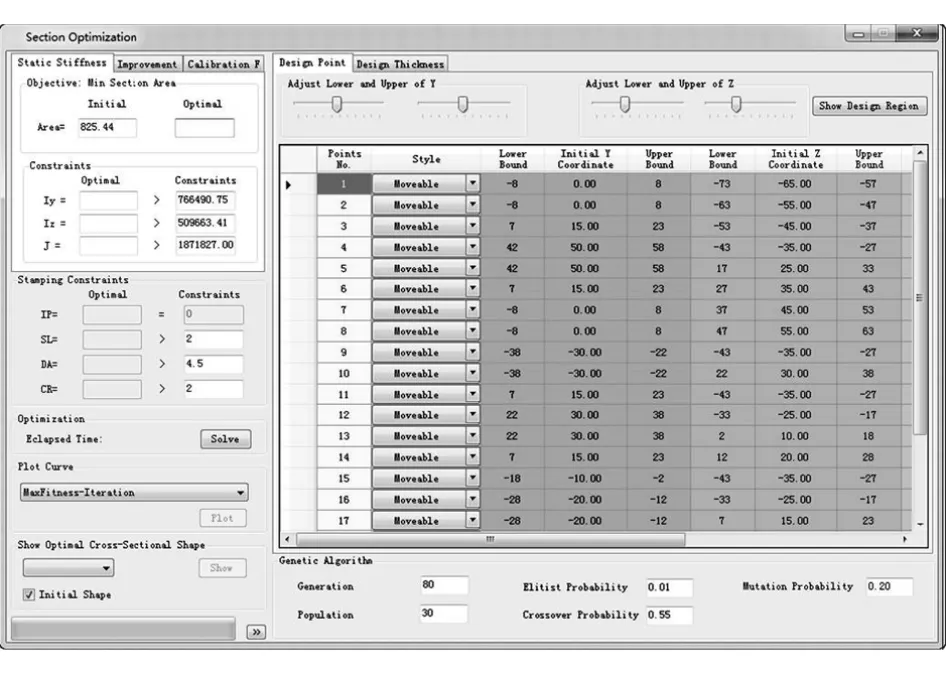
图12 断面形状优化界面图

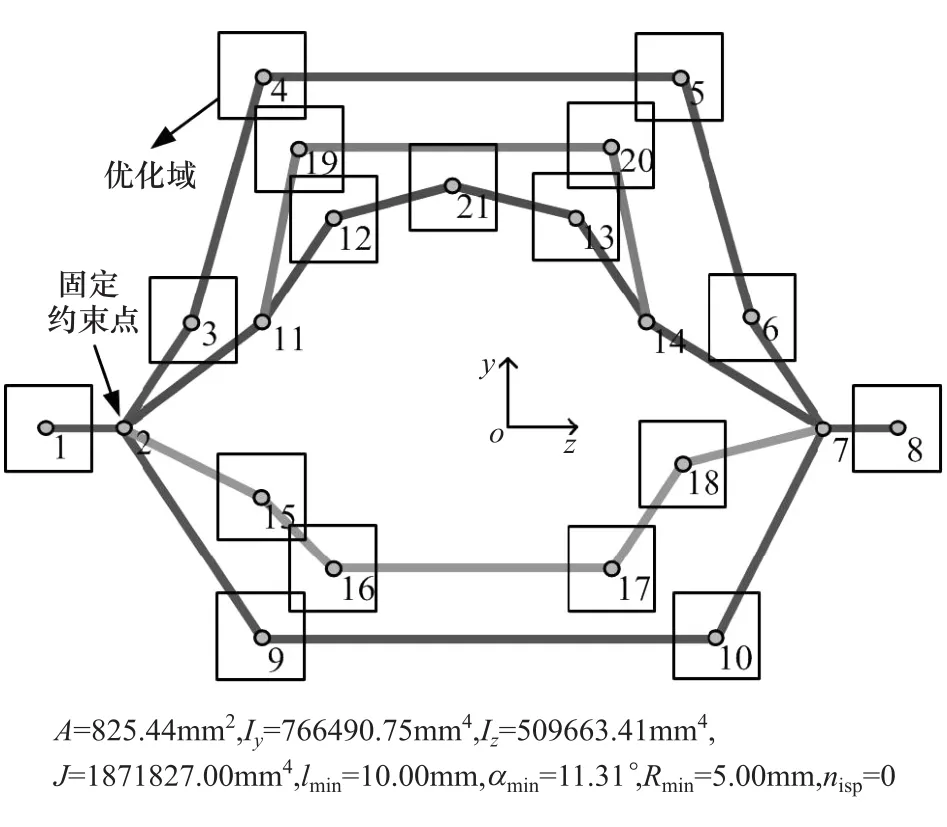
图13 初始断面图

第3,6,36和80次迭代中的断面形状如图14～图17所示。优化结果列于表3。可以看到:在满足最小线段长度约束、拔模角约束、倒圆角半径约束和装配约束下,弯曲惯性矩Iy,Iz,尤其是扭转惯性矩J,都有较大提高,同时断面面积减小,实现了薄壁梁轻量化的目的,算例验证本文建立的优化模型是有效的。计算用时仅为178.6s,完全满足概念设计阶段断面快速设计与优化的要求。

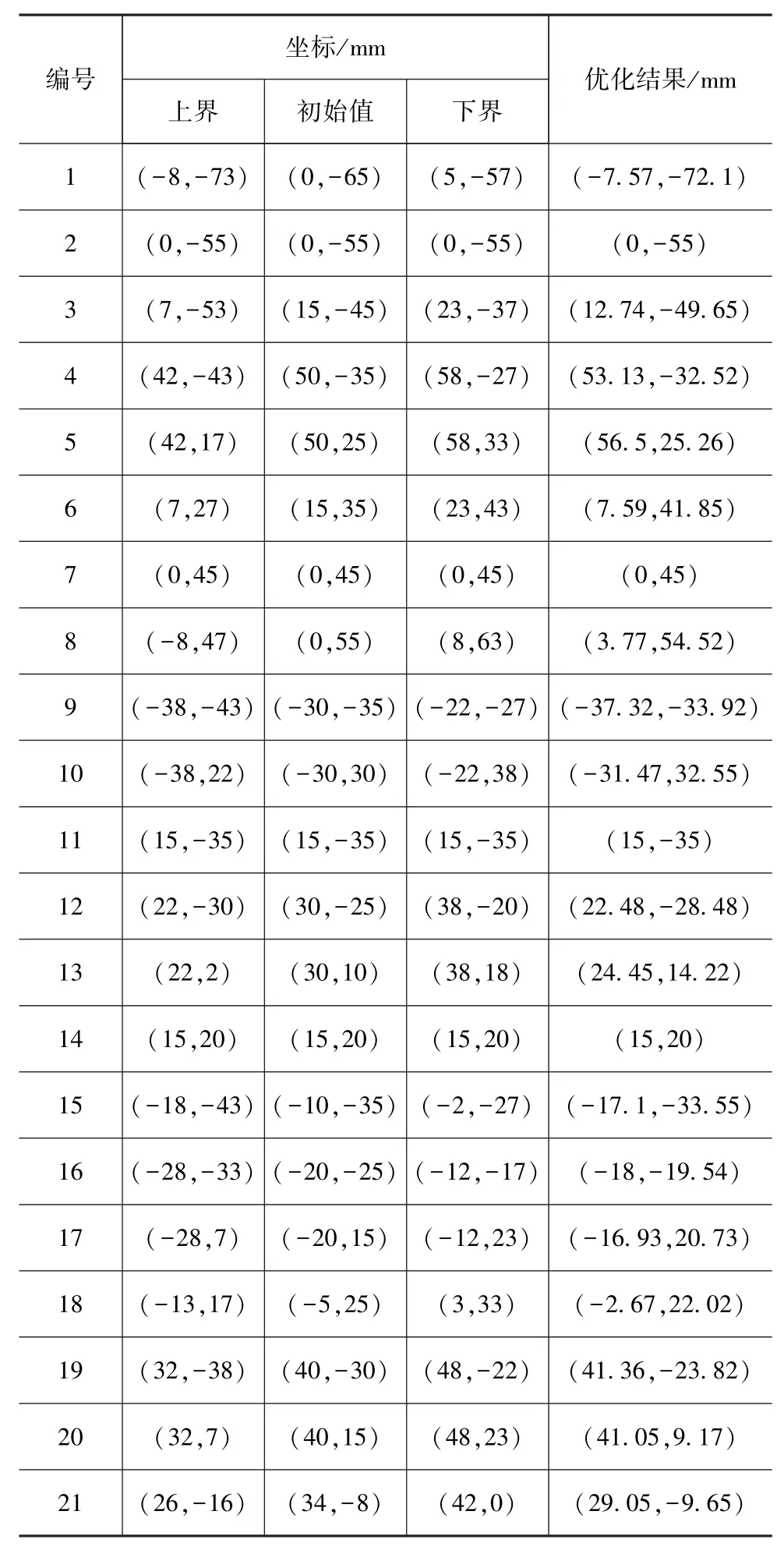
表1 控制点坐标变量和优化结果

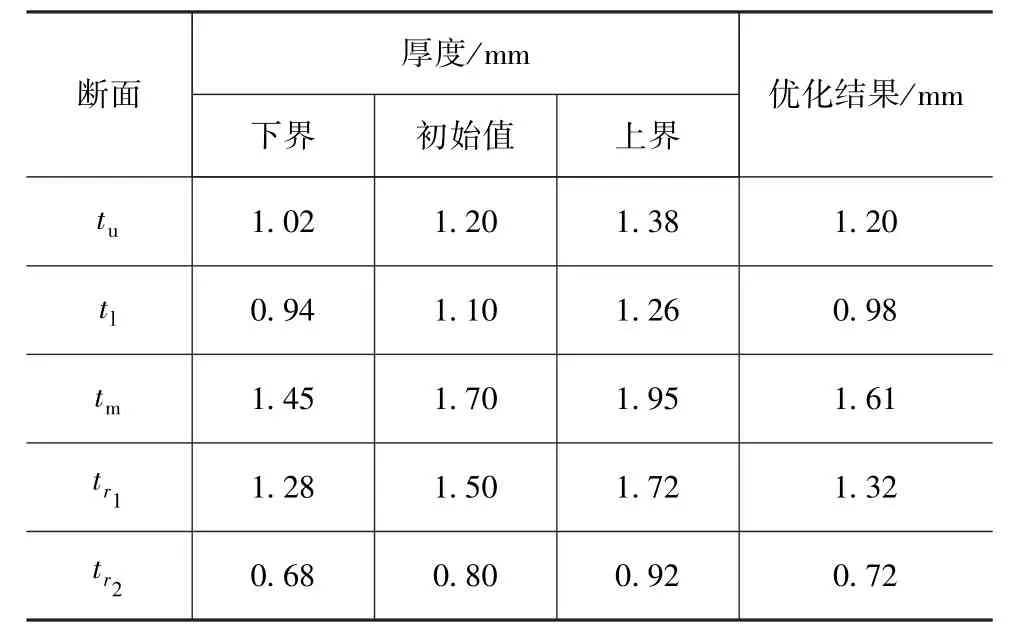
表2 厚度变量和优化结果

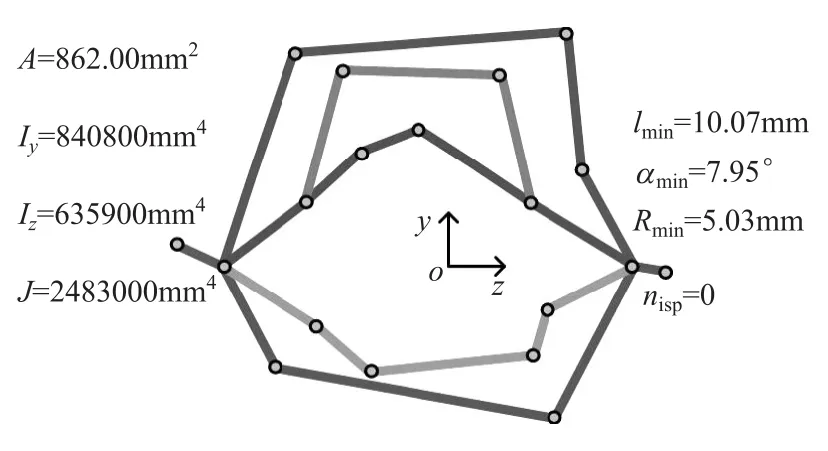
图14 第3次迭代图

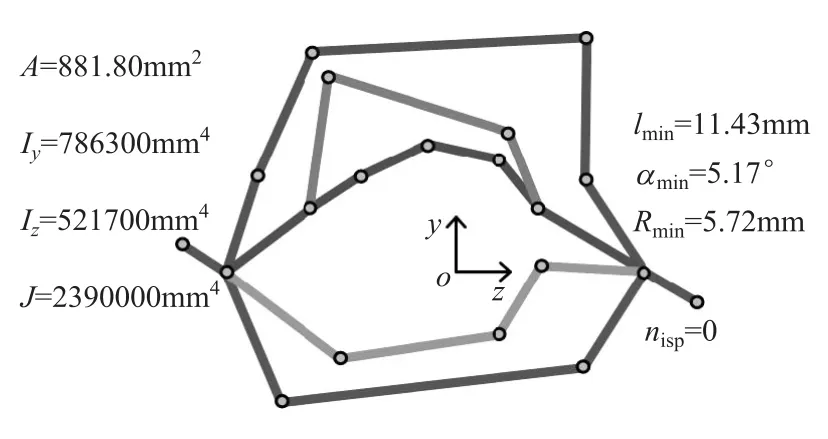
图15 第6次迭代图

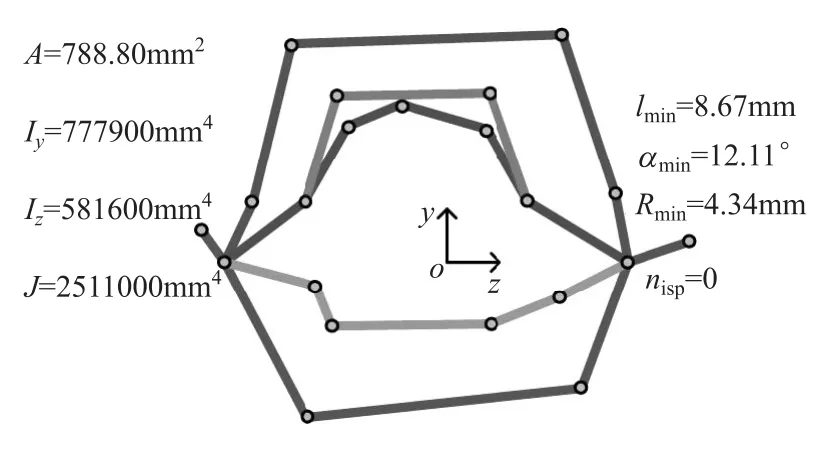
图16 第34次迭代图

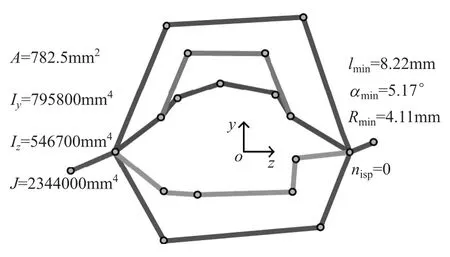
图17 第80次迭代图

5 结论

(1)推导出了开口、单室、双室、三室和四室的薄壁梁断面力学特性公式,包括面积、质心、弯曲惯性矩、惯性积和扭转惯性矩。这是目前作者所知的可求解的腔室最多的断面类型。对冲压工艺约束,如最小线段长度约束、拔模角约束、倒圆角半径约束和装配约束,推导了可量化的数学表达式。

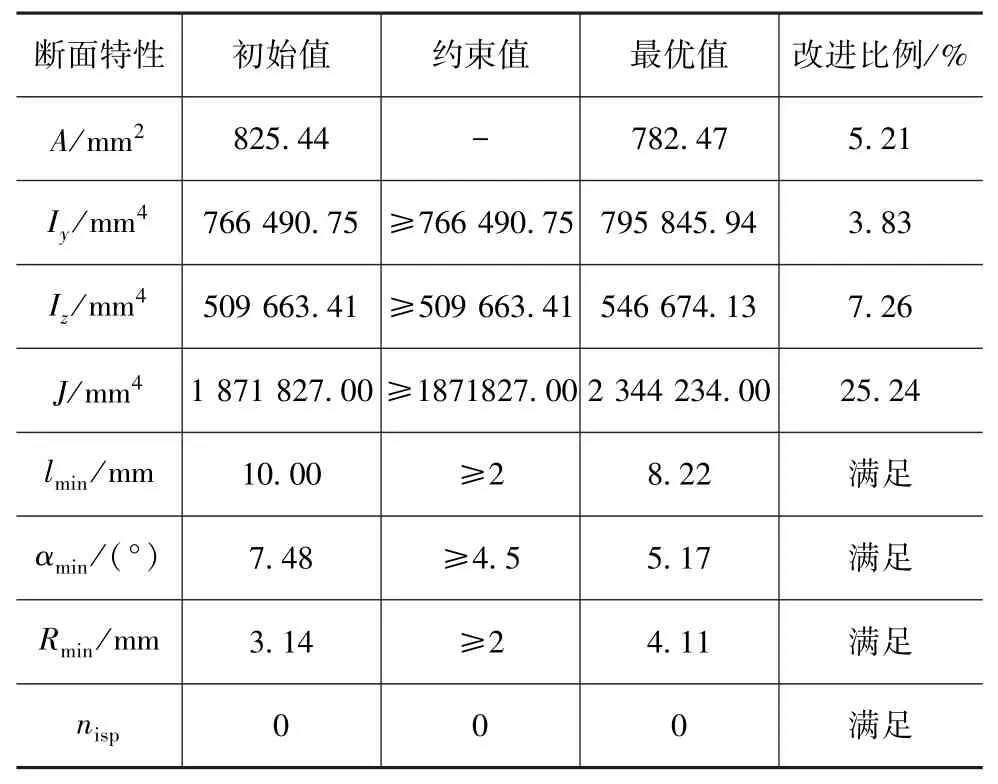
表3 优化前后断面性能比较

(2)在冲压工艺约束下,优化了断面几何形状与板厚,提高了断面弯曲惯性矩和扭转刚度,同时减小了断面面积,实现了薄壁梁的轻量化设计。在普通计算机上,只需要大约3min即可完成断面的形状优化,求解效率满足概念设计的要求。该方法将会提升汽车车身结构正向设计的能力。