单帽型薄壁梁弯曲和轴向压溃吸能的理论预测方法研究∗

胡朝辉,杜展鹏,段利斌,张光亚,武敬伟

(1.湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082； 2.江苏大学汽车与交通工程学院,镇江 212013；3.上汽通用五菱股份有限公司,柳州 545007)

前言

薄壁梁是汽车车身的重要吸能结构,由于其具有强度高、吸能效果好、质量轻等特点而在汽车碰撞安全方面得到广泛应用[1]。在车身结构概念设计的早期阶段,由于缺乏详细的结构几何数据,无法建立车身结构分析和优化模型,使设计人员很难利用有限元分析方法研究车身薄壁结构的吸能特性,无法快速地设计出较优的截面形状,从而指导车身结构的耐撞性设计。因此,研究薄壁梁压溃吸能的理论预测对车身结构耐撞性设计具有重要的指导意义,可以在概念设计早期阶段辅助设计人员快速提取薄壁结构的吸能特性,指导截面设计,实现对设计方案前期进行快速评估和及时修改,缩短汽车车身的开发周期。

早在20世纪60年代,Alexande JM[2]针对薄壁圆管构件进行了轴向压溃试验,探究其轴向压溃性能,并建立了预测薄壁圆管构件轴向渐进性溃缩变形特性的理论模型。Wierzbicki等[3]基于宏单元法,提出SE理论,成为薄壁梁理论分析的基础。White等[4]基于SE理论,根据能量守恒定律得到单一厚度低碳钢帽型结构的准静态轴向压溃力理论公式。在薄壁梁横向弯曲压溃的机理研究方面,Kecman[5]针对矩形和方形截面薄壁梁做了大量弯曲试验,对矩形薄壁梁的弯曲变形模式进行了详细分析,并提出了固定铰线和滚动铰线的概念。高元明[6]则在Kecman理论模型的基础上研究了双帽型截面薄壁梁的抗弯特性,进一步丰富了薄壁梁的弯曲压溃理论。李亦文[7]与 Abramowicz[8]一样,在 Kecman理论模型的基础上,提出了一种箱型截面薄壁梁弯曲特性分析的方法,使理想塑性弯曲区域的面内变形满足运动学容许的条件。Liu Y C和Day M L针对槽型[9]、圆形[10]和锥形[11]等不同截面形式的薄壁梁进行了探究,并推导出相应的弯曲压溃吸能理论公式。虽然前人对帽型薄壁梁弯曲压溃和轴向压溃理论进行了较多的研究,也取得了较大成果,但针对单帽型薄壁梁弯曲压溃和轴向压溃的理论模型构建仍然不够合理,且都无法解决同材异厚、异材同厚、异材异厚的单帽型薄壁梁弯曲压溃和轴向压溃吸能的理论预测问题。

针对以上单帽型薄壁梁弯曲压溃和轴向压溃吸能的理论预测方法的不足和局限性,本文中以Kecman薄壁梁弯曲压溃理论[5]和Wierzbicki超折叠单元(superfolding element,SE)理论[3]为基础,建立了一种改进的单帽型薄壁梁准静态弯曲压溃和轴向压溃理论模型,并推导了单帽型薄壁梁的弯曲压溃和轴向压溃吸能公式。通过将单帽型薄壁梁结构分解为基本帽型单元和平板单元,使改进的理论模型能适用于求解同材同厚、同材异厚、异材同厚和异材异厚的单帽型薄壁梁弯曲压溃和轴向压溃吸能的理论预测。

1 单帽型薄壁梁弯曲压溃改进理论预测模型

为解决同材同厚、同材异厚、异材同厚和异材异厚的单帽型薄壁梁弯曲压溃吸能的理论预测问题,将单帽型薄壁梁结构按照变形模式的不同划分为基本帽型单元和平板单元,如图1所示。

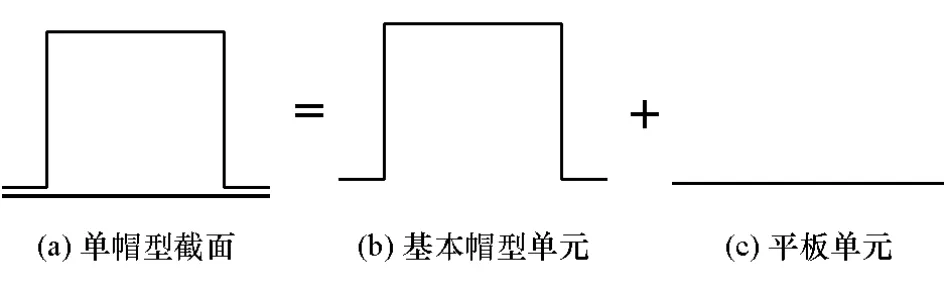
图1 单帽型薄壁梁单元分解

1.1 单帽型薄壁梁弯曲压溃理论模型

根据单帽型薄壁梁的弯曲变形特点,并结合Kecman的薄壁梁弯曲压溃理论[5],建立了一种改进的单帽型薄壁梁准静态弯曲压溃理论模型,如图2所示。其中,图2(b)为基本帽型单元的弯曲压溃褶皱模型,考虑到结构轴向对称性,仅列出基本帽型单元的一半轴向对称的简化弯曲压溃理论模型。图2(c)为平板单元的弯曲压溃褶皱模型。根据单帽型薄壁梁弯曲压溃过程中的变形特点,可将基本帽单元在弯曲压溃过程形成的塑性铰线分为固定铰线和滚动铰线。其中,线段AK,AL,AB,BC,GH,EF,KL,KK1和LL1为固定铰线,线段AG和AE作为滚动铰线,如图2(b)所示。

当单帽型薄壁梁发生弯曲压溃时,可以认为平板单元中线段K2L2和N2M2与基本帽型单元中的线段KL和K1L1一样始终保持为直线,且长度不变。随着塑性转角 θ的持续增大,形成铰线 K2N2和L2M2。因此,在平板单元弯曲压溃褶皱模型中,将线段K2N2和L2M2作为固定铰线,如图2(c)所示。

1.2 弯曲压溃吸能计算

根据Kecman薄壁梁弯曲压溃理论[5],薄壁梁弯曲压溃过程中的能量全部消耗在固定铰线和滚动铰线上。

1.2.1 基本帽型单元的吸能计算基本帽型单元固定铰线吸收的能量为

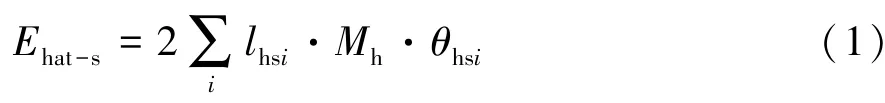
式中:i为固定铰线的数量；lhsi为基本帽型单元固定铰线的长度,mm；Mh为基本帽型单元材料的单位长度塑性极限弯矩,N,且,其中 σ 为基本h-b帽型单元材料的抗拉强度；th为基本帽型单元材料的厚度,mm；θhsi为基本帽型单元固定铰线的塑性转角,rad。

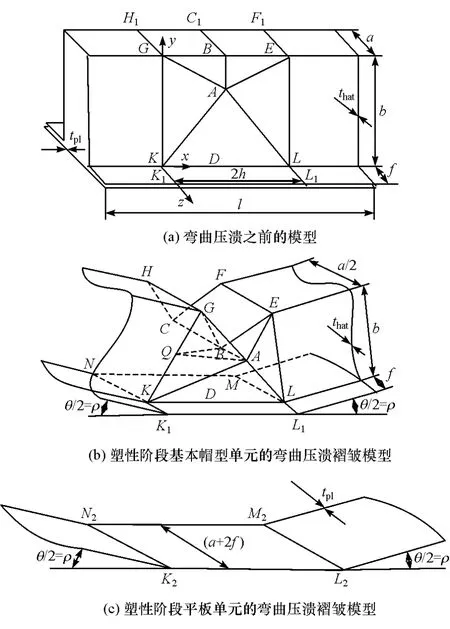
图2 单帽型薄壁梁准静态弯曲压溃理论模型

基本帽型单元滚动铰线吸收的能量为

式中:Δhsi为基本帽型单元滚动铰线i扫过的面积,mm2；r为滚动铰线的滚动半径,mm。r的近似值[3]为

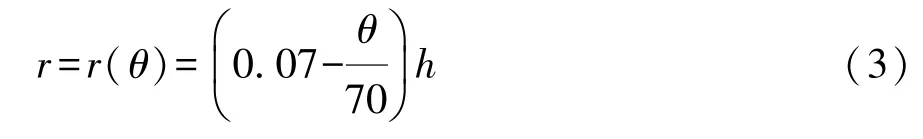
则基本帽型单元弯曲压溃过程中吸收的总能量Ehat为

1.2.2 平板单元的吸能计算

在平板单元弯曲压溃褶皱模型中,只有固定铰线K2N2和L2M2,如图2(c)所示。

平板单元固定铰线吸收的能量为

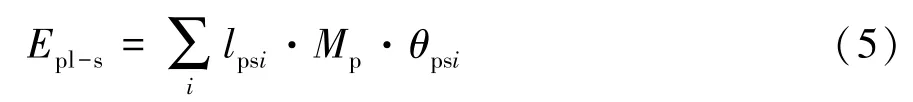
式中:lpsi为平板单元固定铰线的长度,mm；Mp为平板单元材料的单位长度塑性极限弯矩,N,且Mp＝,其中σ 为平板单元材料的抗拉强度,t为

p-b

p平板单元材料的厚度；θpsi为平板单元固定铰线的塑性转角,rad。

由于平板单元中没有形成滚动铰线,因此平板单元滚动铰线吸收的能量为

则平板单元弯曲压溃过程中吸收的总能量Epl为

则单帽型薄壁梁弯曲压溃过程中吸收的总能量EB为

2 单帽型薄壁梁轴向压溃改进理论预测模型

2.1 单帽型薄壁梁轴向压溃理论模型

根据单帽型薄壁梁的轴向压溃变形特点,结合Wierzbicki等[3]的SE理论,可将基本帽型单元分解为4个如图3(a)所示的SE单元。由于平板单元在压溃过程中产生弯曲变形,基于Chen等[12]的研究,其折叠过程形成3条固定铰线,如图3(b)所示。

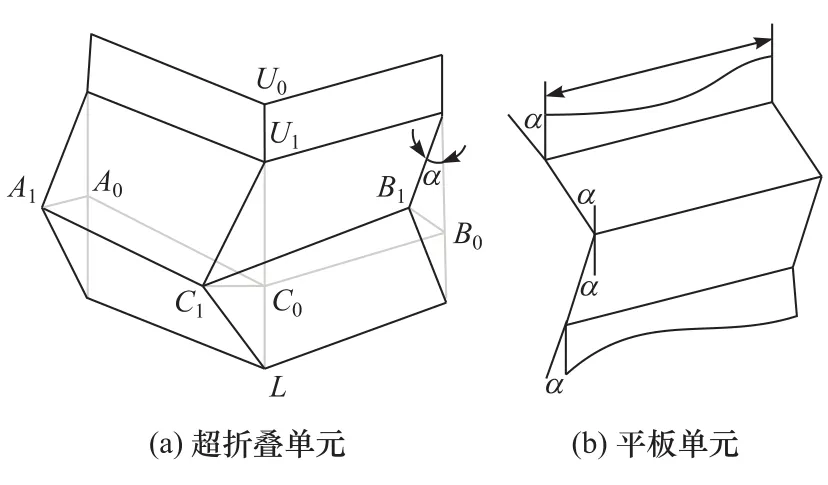
图3 单帽型薄壁梁轴向压溃理论模型

2.2 轴向压溃吸能计算

2.2.1 基本帽型单元的吸能计算

如图1(b)所示,基本帽型单元由4个L型直角单元组成,即可分解为4个SE进行吸能求解。如图3(a)所示,基于Wierzbicki等[3]的SE理论,定义变形过程中折叠波长为2H,则一个SE在变形过程中所吸收的能量为

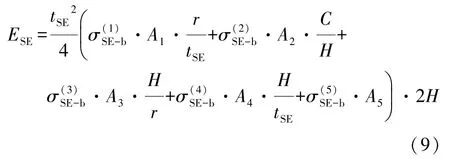
式中:tSE为超折叠单元材料的厚度,mm；为超折叠单元材料不同变形区域的抗拉强度,MPa；H为折叠过程中塑性半波长；r为变形过程中的滚动半径,mm；C为超折叠单元两个折边的长度之和,mm；Ai为与变形模式及几何参数有关的支配解。

White等[4]的研究成果表明,夹角为90°的超折叠单元中,A1＝4.44,A2＝π,A3＝2.296,A4＝A5＝0,因此直角超折叠单元变形所吸收的能量为

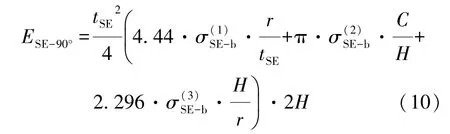
由于基本帽型单元可看成由4个SE构成,当基本帽型单元在轴向压溃量为2H时,其吸收的能量为

2.2.2 平板单元的吸能计算

如图3(b)所示,平板单元在弯曲过程中通过3条固定铰线进行吸能,其吸收的能量为

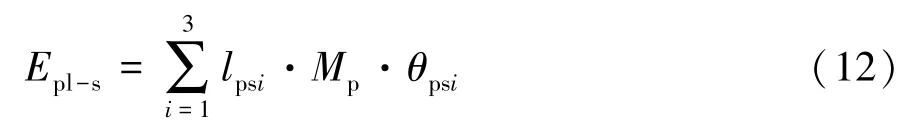
当轴向变形量为2H时,平板单元被完全压溃,因此固定铰线产生的旋转角度θ＝π/2,可求得平板单元吸收的能量为

式中:Mp为平板单元材料的单位长度塑性极限弯矩,N,且 其中σ 为平板单元材料的抗p-b拉强度,tp为平板单元材料的厚度；lps为平板单元固定铰线的长度,mm。

则单帽型薄壁梁轴向压溃过程中吸收的总能量E A为

3 改进理论预测公式验证

3.1 弯曲压溃和轴向压溃试验

试验样件采用HC340LA材料,长度l＝400mm,壁厚t＝1.6mm,焊点间距为 30mm,翼缘宽度 a＝105mm,腹板高度b＝85mm,翻边宽度f＝35.7mm的单帽型薄壁梁,其截面尺寸如图4所示。三点弯曲试验如图5所示。试验过程中,压头的速度恒为5mm/min,为保证薄壁梁完全压溃,将压头的压溃距离设为60mm。轴向压溃试验如图6所示,试验过程中,压头的速度恒为5mm/min,为保证薄壁梁完全压溃,在280mm处设置限位机构。

图6 单帽型薄壁梁轴向压溃试验

3.2 弯曲压溃和轴向压溃有限元模型的建立

利用LS-DYNA软件建立单帽型薄壁梁的弯曲压溃和轴向压溃有限元模型,如图7所示。单帽型薄壁梁采用MAT24号材料[13],厚度方向采用5个积分点。将薄壁梁弯曲压溃有限元模型中的压头和支撑圆柱以及轴向压溃模型中的压板和支撑板视为刚性,采用MAT20号材料[13],所有部件的网格大小均设为4mm。

3.3 弯曲压溃和轴向压溃有限元模型的验证

仿真与试验结果的对比如表1和图8～图11所示。根据表1和图8以及表1和图10的对比结果可知,单帽型薄壁梁的弯曲压溃试验和轴向压溃试验与各自仿真的吸能结果和吸能过程都表现出了较高的一致性。从图9和图11可知,单帽型薄壁梁有限元模型的变形模式与试验结果的一致性较好。综上所述,本文中建立的弯曲压溃和轴向压溃有限元仿真模型可较真实地还原试验过程,具有较高的模拟精度,可在后续研究中代替物理试验过程。

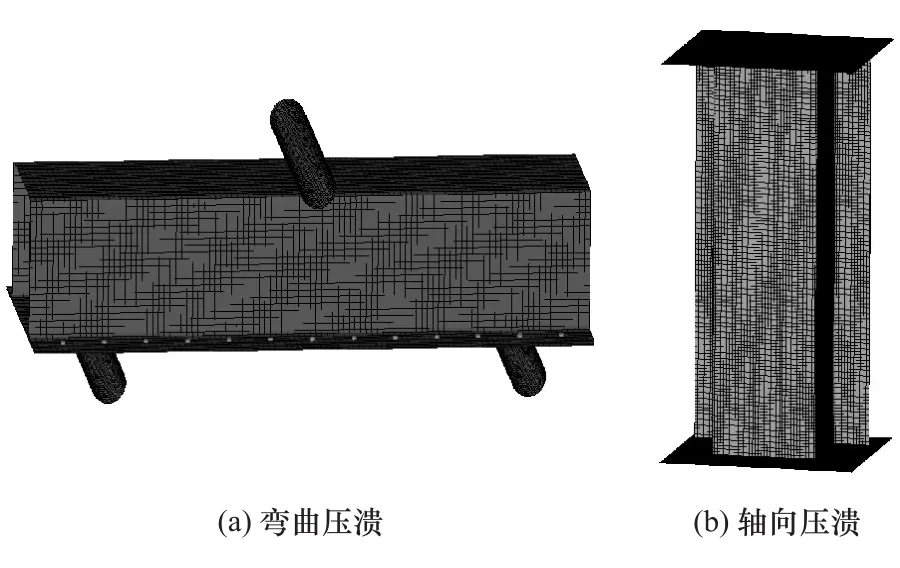
图7 单帽型薄壁梁有限元模型

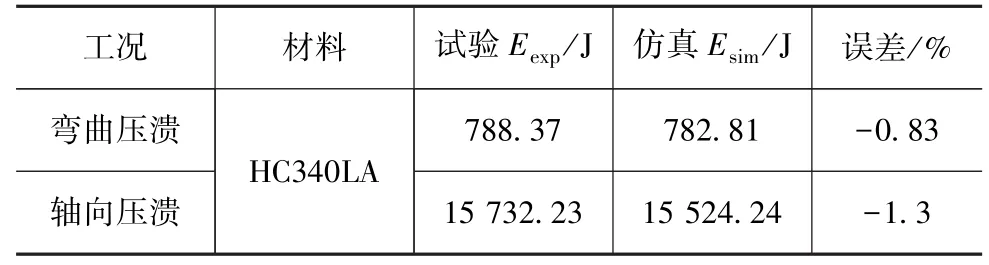
表1 压溃试验与有限元仿真的吸能结果对比

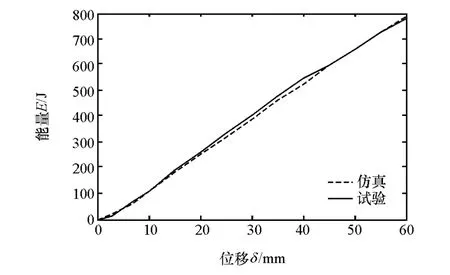
图8 弯曲压溃试验与仿真吸能-位移曲线对比

3.4 弯曲压溃和轴向压溃吸能公式验证

3.4.1 弯曲压溃吸能公式验证

单帽型薄壁梁的屈服强度σs和抗拉强度σb分别为359和439MPa,其中,弯曲压溃试验结束时,薄壁梁弯曲转角为0.398rad。根据式(8)可求得该帽型薄壁梁总吸能为813.85J。该单帽型薄壁梁结构的试验、仿真和理论预测的吸能对比结果详见表2和图12。

由表2可知,该单帽型薄壁梁的弯曲压溃吸能理论预测值相对试验和仿真结果的误差在5%以内。由图12可知,试验、仿真和理论预测公式的吸能-转角变化趋势表现出了较高的一致性,且改进理论的计算结果比Kecman的弯曲压溃理论计算结果更接近试验值。上述对比分析结果表明:所推导单帽型薄壁梁的理论吸能公式具有较高的准确性,且计算精度远远高于Kecman弯曲压溃理论。

图9 弯曲变形模式对比

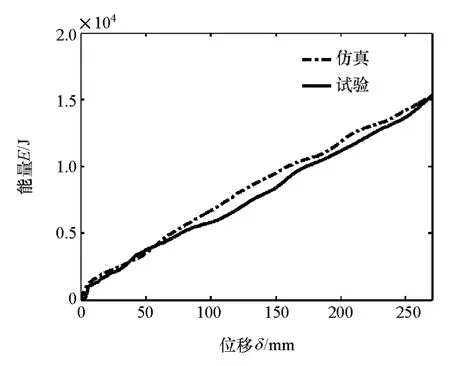
图10 轴向压溃试验与仿真吸能-位移曲线对比

图11 轴向变形模式对比

表2 弯曲压溃吸能结果对比 J

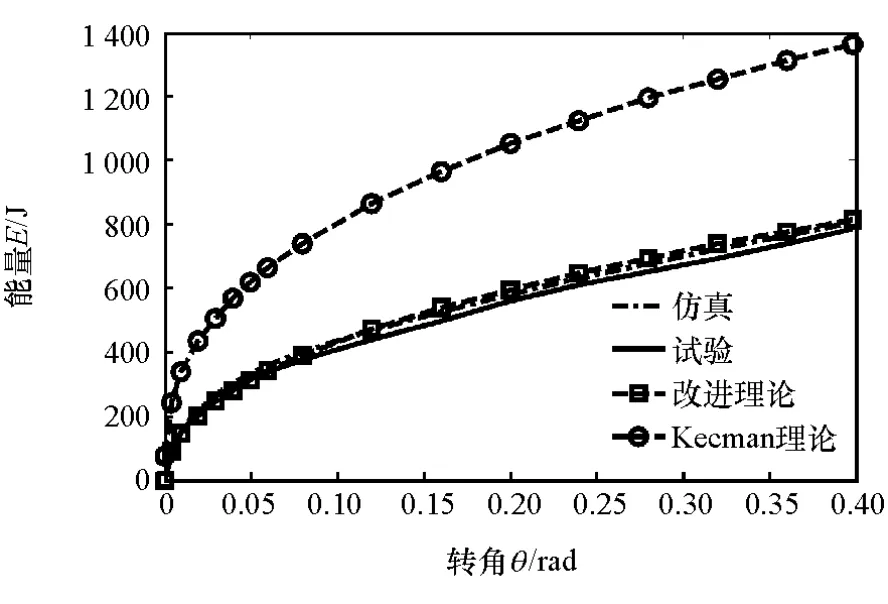
图12 弯曲压溃吸能结果曲线对比

3.4.2 轴向压溃吸能公式验证

根据式(14)可求得该帽型薄壁梁总吸能为15 647.76J。该单帽型薄壁梁结构的试验、仿真和理论预测的吸能对比结果详见表3。

表3 轴向压溃吸能结果对比 J

由表3可知,该单帽型薄壁梁的轴向压溃吸能理论预测值相对试验和仿真结果的误差在5%以内。表明所推导单帽型薄壁梁的理论吸能公式具有较高的准确性。

4 压溃吸能改进理论预测公式的通用性验证

4.1 验证方案

由于物理试验的成本较高,利用3.2节建立的有限元模型求解不同材料、不同截面尺寸和不同厚度的单帽型薄壁梁在弯曲压溃和轴向压溃工况下的吸能,并与相应理论预测公式计算的结果进行比较,进而验证单帽型薄壁梁弯曲压溃吸能理论预测公式的通用性。

分别选用3种不同材料、不同截面尺寸、不同厚度的单帽型薄壁梁结构作为弯曲压溃和轴向压溃方案样件,如表4所示。涵盖了a＞b,a＝b和a＜b的不同截面尺寸情况以及同材同厚、同材异厚、异材同厚和异材异厚的不同基本帽型单元与平板单元的组合情况,因此本验证方案能够较为全面地验证所提出理论公式的通用性。

4.2 结果分析

基于式(8)和式(14)分别对表4的单帽型薄壁梁的弯曲压溃和轴向压溃总吸能进行计算,并与有限元仿真结果进行对比,如表5所示。从表5中可以看出,改进理论预测公式计算得出的吸能值与有限元仿真结果相当接近,误差都在5%以内,说明本文推导的单帽型薄壁梁弯曲压溃和轴向压溃吸能理论预测公式对同材同厚、同材异厚、异材同厚和异材异厚各种场合都有足够的精度,即在应用范围方面更具有通用性。

5 结论

(1)建立了一种改进的单帽型薄壁梁准静态弯曲压溃和轴向压溃理论模型,并推导了单帽型薄壁梁的弯曲压溃和轴向压溃吸能公式。研究结果表明:改进的理论模型对于预测单帽型薄壁梁的弯曲压溃和轴向压溃吸能具有较高的精度。

(2)将单帽型薄壁梁结构按照变形模式的不同划分为基本帽型单元和平板单元,通过分别推导基本帽型单元和平板单元的弯曲压溃和轴向压溃吸能公式,得到单帽型薄壁梁弯曲压溃和轴向压溃总吸能,使改进的理论模型适用于求解同材同厚、同材异厚、异材同厚和异材异厚的单帽型薄壁梁弯曲压溃和轴向压溃吸能。

(3)利用已经得到准确性验证的有限元模型求解不同材料、不同截面尺寸、不同厚度的单帽型薄壁梁的弯曲压溃和轴向压溃吸能,并与理论预测值进行对比分析,误差均在合理范围之内,验证了本文推导的单帽型薄壁梁弯曲压溃和轴向压溃吸能理论预测公式在应用范围方面更具有通用性。