浅谈制动踏板机构设计

朱鹏程、赵卫晨、韦振举、覃春好

（1. 上汽通用五菱汽车股份有限公司 545007；2. 广西艾盛创制科技有限公司 545007)

0 引言

制动踏板在设计过程中,经常出现输入条件的变更。了解制动踏板的受力情况，可以对输入条件变更带来的影响进行初步评估，使踏板的结构设计更有方向性。除此之外，还可以对最大应力、变形区域进行预判，并与CAE分析结果相比对，判断其分析结果是否具有合理性。

1 踏板机构

如图1所示，制动踏板主要由踏板杆、踏板支架、轴销、衬套、回位弹簧和衬套等零件组成。

1.1 踏板杆

踏板杆常见结构有非断开式踏板杆与断开式踏板杆（图2）。其中，断开式踏板的结构主要是为了避让转向系统的中间轴和传动轴等零件；而非断开式踏板杆相对断开式踏板结构更简单，质量更轻。

1.2 踏板支架

踏板支架根据使用的材料分为塑料踏板支架与金属踏板支架（图3），塑料踏板支架成型精度高，质量小，但成本高。

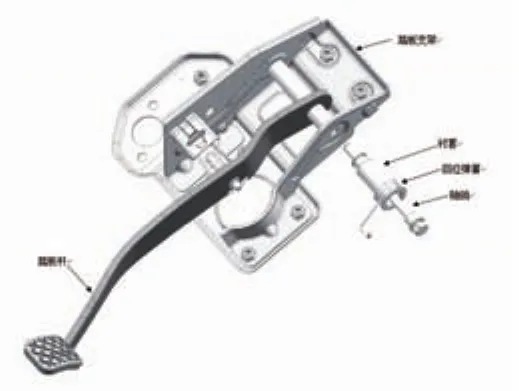
图1 制动踏板结构

图2 非断开式踏板杆（左）和断开式踏板杆（右）

图3 塑料支架（左）和金属支架（右）

2 踏板杆受力情况

2.1 非断开式踏板杆

如图4、图5所示，该踏板杆为非断开式踏板杆，它静止地处于1/2全行程位置上。O点为踏板旋转点，Q为推杆“U”型叉与踏板杆接触点，H点为踏板面中心点。Ft为踏板力（假设踏板力过踏板H点，并垂直于踏板面），FQ为助力器推杆对踏板的支持力。FO为踏板支架对踏板杆的作用力。a为输入力臂，b为输出力臂，c为踏板面中心H点到Q点的距离。踏板杠杆比i=a/b，杠杆比是影响踏板感觉的重要因素，不轻易修改[1]。

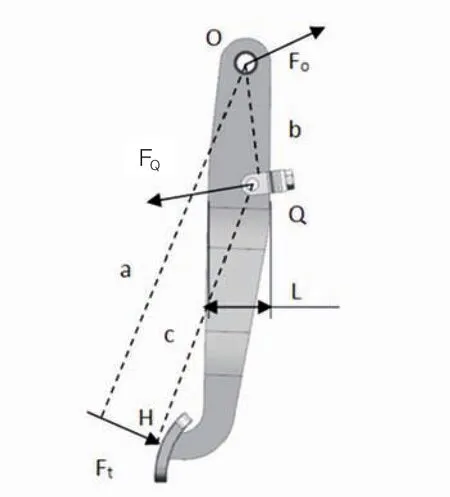
图4 非断开式踏板受力情况

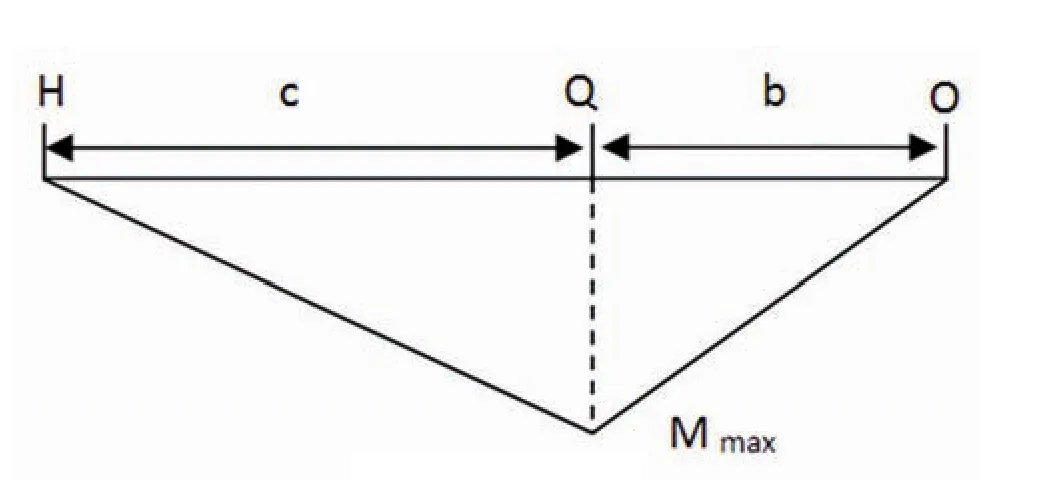
图5 踏板杆弯矩图

踏板杆的最大弯矩为如下。

将踏板杆的截面看似成矩形，其高为h（板厚方向）、宽为L，则抗弯截面系数为如下。

踏板杆截面最大正应力如下。

由公式(1)～公式(3)可知，在Q点附近踏板杆弯矩最大。弹性变形最大的区域一般在踏板面。为了避免Q点附近应力变形过大而导致踏板面弹性变形过大，在保持材料、杠杆比不变的情况下，尽量减小c与b的值（满足助力器主缸行程下），从而降低弯矩Mmax。还可以增加踏板杆宽度或厚度降低正应力，其中，增加宽度效果会更明显些。踏板杆宽度从Q点区域至H、O点区域逐渐减小，不仅提高了材料利用率还减少了踏板杆质量。

2.2 断开式踏板杆

如图6所示，断开式踏板杆由输入杆、转轴、输出杆组成，踏板力通过它们最终传递给真空助力器。因此不仅要考虑输入杆、输出杆弯矩，还要考虑转轴的扭矩。

断开式踏板转轴扭矩如下。

转轴圆截面的切应力如下。

转轴扭转角如下。

式中，D为圆管的外圆直径；d为圆管的内圆直径；Wt为抗扭截面系数；Lg为两踏板杆之间的圆管长度；G为切变模量，可以通过弹性模量与泊松比求出；Ip为对于圆心的极惯性距，对于空心圆钢，Ip计算如下。

由公式(1)～公式(3)可知，输入杆、输出杆最大弯矩会出现在转轴附近。因此踏板杆的宽度由O点到H点、Q点逐渐减小，如图7所示。在保持材料、杠杆比不变的情况下，尽量减小a与b的值（满足助力器主缸行程下），可以有效地降低扭矩T。也可以通过增大内径、外径有效地提高抗扭截面系数Wt，从而降低切应力。横截面上的切应力沿半径按线性规律分布，圆心附近的应力很小，材料没有充分发挥作用。弹性变形最大的区域一般在踏板面。在保证材料不变的情况下，除了修改a、b、L三值可以改善变形外，还可以通过增加极惯性距Ip或者减小杆间距Lg，达到减少变形、质量的目的。

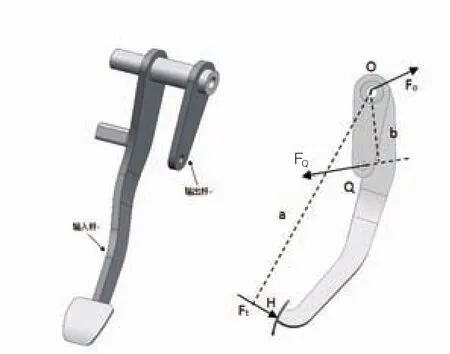
图6 断开式踏板杆

图7 变截面踏板杆

3 踏板支架受力情况

如图8所示,踏板力Ft在FQ右侧，要想满足平衡，踏板支架对踏板杆的作用力FO必须位于FQ左侧。踏板杆对踏板支架的合力为Ff，是FO的反作用力。Ff到O1转轴的轴向距离为k，到O2的距离为e。转轴对踏板O1处的拉力为FO1，O2处的拉力为FO2。根据受力平衡有，Ff= FO1+ FO1。

因为k＜e，所以FO1＞ FO2，左侧的踏板支架相对右侧的支架受力情况更较恶劣。在材料不变的情况下，可通过增加加强筋、板厚等方式提高左侧支架的强度与刚度。而右侧的支架在满足强度刚度的情况，着重考虑轻量化结构。

如图9所示，FQ1为踏板杆对真空助力器的力，是FQ的反作用力。真空助力器通过螺母与B1、B2、C1和C2四个安装点连接。很显然，A1点和A2点受到的是拉力，并且A1点受到的拉力比A2点更大。解决这两个点附近区域应力大的方法主要有2种：一是减小两点受到的拉力，如增加u的值；二是加强两点附近区域的刚度，如采用板厚更大的支架与两点相接，再通过焊接将该支架与其他支架相连接。因为受到的是拉力，通过增加接触面积方式是无法有效地改善该区域的应力情况。

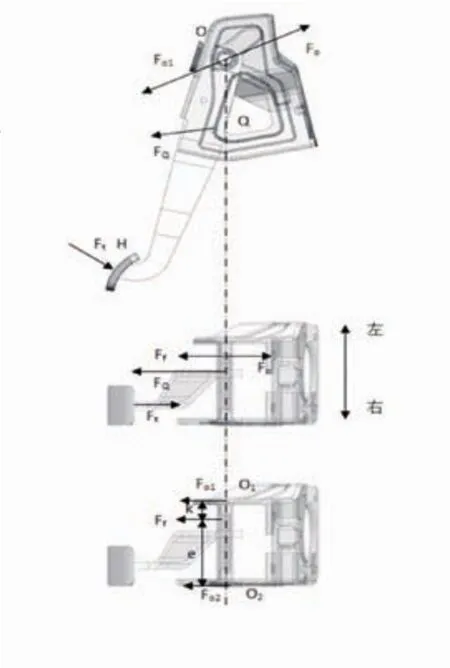
图8 踏板支架受力情况

图9 踏板支架

4 结束语

制动踏板受力情况会随着结构的不同而有所差异，但是分析方法一样的。了解制动踏板的受力情况，使结构设计更有方向性与目的性[2]。