基于供应链核心企业成本控制的供应链结构优化

（内蒙古工业大学，内蒙古 呼和浩特 010051）

1 引言

21世纪的竞争不再是企业与企业之间的竞争，而是供应链与供应链之间的竞争。就供应链的结构而言，一般是由一个主导企业（制造商、供应商或零售商）充当企业群体的“原子核”（即核心企业），把其他“卫星”企业吸引在核心企业周围所构成的一个网链。实践证明，供应链运作效率及整个供应链竞争能力的大小，很大程度取决于供应链上核心企业的影响力[1]。供应链核心企业对供应商的不同选择会直接影响到核心企业的采购成本、库存管理成本。供应链核心企业对生产出的产成品的销售环节管理，如销售企业的数量、销售企业的进货方式及库存管理等都会影响到生产企业对成品管理的成本，从而影响到供应链核心企业的库存总成本。以供应链核心企业的库存总成本最小为目标，合理调整供应商的数量和销售商的数量，是供应链管理中一个非常重要的问题。

很多学者对供应链结构问题进行了研究，并取得了一系列成果。如，Stock,et al.（2000）调查了企业物流与供应链结构的关系问题，指出物流是协调供应链运作的必要手段[2]。Ernst和Kamrad（2000）基于模块化和延迟特性，给出了评价四种供应链结构的概念框架[3]。李群明等（2001）对不同供应链体系结构模型，包括供应链作业参考模型（SCOR）、供应链开发模型（SCDM）和供应链管理软件等进行了对比分析[4]。陈剑学者（2002）从单级生产-库存系统、多级生产-库存系统、供应链流程重组三方面对供应链结构问题进行了综述，并提出将来的供应链研究集中于供应链重组和不确定性等问题[5]。张青山等（2002）总结了不同行业中的供应链结构类型，并给出了相应的供应链管理策略[6]。综上所述，之前学者们基本都是从理论上研究供应链结构，而利用仿真手段结合实例对供应链结构进行研究的较少。本文对供应链核心企业为制造业的供应链结构进行仿真优化，首先利用管理领域专业的Witness仿真软件建立供应链仿真模型，再利用模拟退火算法，以核心企业的总库存成本为优化目标，以提供各类原材料的供应商数量和销售产成品的销售商数量为优化变量，对供应链结构进行优化研究。

2 供应链结构与供应链核心企业库存总成本的关系

供应链核心企业在供应链中具有配置资源的权利，比如对供应商的选择、对原材料和成品运输方式的选择以及对原材料进货批次和安全库存的控制等。因而，核心企业有能力对供应链资源进行调整，进而优化供应链的结构，最终实现核心企业总库存成本最小。某一种原材料从一个或多个供应商购买会影响到这种原材料的采购成本，影响到原材料的实时库存量，从而影响到原材料的库存保管费和缺货损失费。同时，供应链核心企业选择销售产成品的销售企业的数量会直接影响到核心企业产成品的库存保管费和成品的缺货损失费。而供应链核心企业的库存总成本构成如下：

核心企业的库存总成本=原材料库存总成本+成品库存总成本

原材料库存总成本=原材料的采购成本+原材料的库存保管费+原材料的缺货损失费

产成品库存总成本=产成品的库存保管费+产成品的缺货损失费

对核心企业库存总成本各项进行数学分析：

按月（按30天计算）订货，每月月初检查库存水平，若库存量I低于下限L订货，高于下限不订货，设库存上限为S，订货量Z为：

假设原材料的采购成本为C1，每件订货费为m，订货附加费为K，则原材料采购成本计算公式为：

假设库存保管费为C2，每件存货每天的保管费为h，系统运行的天数为n，则库存保管费的计算公式为：

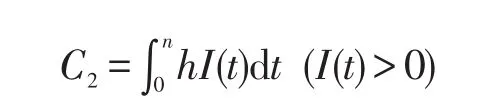
假设原材料或产成品的缺货损失费为C3，每件原材料或产成品每天的缺货损失费为p，则缺货损失费计算公式为：

3 模拟退火算法适合解决供应链结构优化问题

模拟退火算法是一种通用、高效、健壮、可行的拟物型随机近似算法，主要适合求解自然科学、管理科学和工程技术等科技领域普遍存在的组合优化问题。

本文以供应链核心企业的总库存成本为优化目标，以上游供应商数量和下游销售商数量为约束条件，对供应链的结构进行优化，以实现在供应链核心企业总库存成本最小时，选择最佳供应商数量和销售商数量。这个问题属于典型的组合优化问题。所以，本文采用模拟退火算法进行供应链结构优化研究。

4 建立供应链结构优化模型

4.1 供应链实例

以核心企业是生产制造业的供应链为例，供应链核心企业的产品生产需要三种原材料，每月月初检查库存，库存量低于安全库存就发出订货请求。每种原材料可以从一家或多家供应商购买，生产出的产品卖给多家产品销售企业。销售企业也是月初检查库存，库存量高于安全库存不订货，低于安全库存就发起订货请求。供应链运作流程及数据如下：

供应链核心企业（生产企业）：生产企业依据产成品库存数量决定是否进行生产，产成品库存量小于200件时进行生产，三种原材料按1∶2∶3配比生产出一件产成品，生产一件产成品的时间服从1-3天的均匀分布。三种原材料在生产企业的库存上限分别为200件、400件、600件，库存下限分别为100件、200件、400件。每月初检查库存，小于库存下限向生产企业订货，订货量为库存上限与现有库存量的差额。三种原材料的缺货损失分别是2元/件/天，库存保管成本分别是1.5元/件/天，三种原材料采购成本分别为100元/次、200元/次、300元/次。成品的缺货损失为2元/件/天，库存保管成本1.5元/件/天。

原材料供应商：各原材料供应商根据自己的库存量决定是否生产，达到最大库存量停止生产。三家原材料供应商最大库存量分别为300件、500件、700件；生产效率分别为15件/天、40件/天、60件/天。

产成品销售企业：三家销售企业的库存下限都是80件，库存上限都是100。每月初检查库存，小于库存下限向生产企业订货，订货量为库存上限与现有库存量的差额。各销售企业销售成品的效率为1-10件/天。

4.2 建立供应链仿真模型

4.2.1 定义元素。Witness仿真软件是用各类元素来构建仿真模型，如离散型元素、连续性元素、逻辑型元素等。建立仿真模型的第一步就是定义所需要的各类元素，本文所要建立的供应链仿真模型需要定义的元素有30多个，在此不便一一列出，表1仅列出使用模拟退火算法优化时优化目标和约束条件所用到的元素。

4.2.2 建立并调试仿真模型。仿真模型可视化设置如图1所示。根据供应链实例所建立的仿真模型，运行大约600仿真时间，整个供应链仿真系统运行进入常态化，所以将仿真模型的预热时间设置为700仿真时间。

表1 元素定义

图1 供应链可视化仿真模型

4.3 基于模拟退火算法的优化设计

4.3.1 优化目标设置。优化目标是供应链核心企业库存成本kucun最小，优化目标表达式如下：

Min kucun=dy1+dy2+dy3+qh1+qh2+qh3+qh4+gysc1+gysc2+gysc3+cpcc

优化目标在仿真模型中的设置方式为：在仿真系统中打开已定义好的元素“kucun”,如图2所示，点击“Actions”按钮，设置优化目标函数的表达式为“RETURN dy1+dy2+dy3+qh1+qh2+qh3+qh4+gysc1+gysc2+gysc3+cpcc”,如图3所示。

4.3.2 优化约束条件设计及优化其它参数设置。优化约束条件设置见表2。

图2 目标函数“kucun”细节设置页面一

图3 目标函数“kucun”细节设置页面二

表2 优化变量取值

图4是仿真模型中优化模块的详细设置界面，优化约束条件在仿真模型中的设置如图4中“Variables”栏所示；在“Objective Function”中选择优化目标函数“kucun”并选择最小解“Minimun”；在“Algorithm”算法栏中选择模拟退火算法“Adaptive Thermostatistical SA”；根据仿真模型调试数据，将模型预热时间“Warmup”设置为700天，正常优化运行时间“Run”设置为365天（1年）。从图4可以看出，利用模拟退火算法求供应链库存成本最小，共有432种资源配置方案，然后点击运行按钮“Optimize”运行优化算法来获得最优解。

图4 优化设置界面

4.4 利用模拟退火算法进行优化及优化结果分析

从图5可以看出，模拟退火算法运行完432个资源配置方案后，得到的供应链库存成本最小值“Objective Best”为：2 832 652元。优化结果二维图（如图5所示）横坐标是优化方案数，纵坐标是优化目标值，折线显示了不同优化方案所得到的目标值，下方直线是最优目标值曲线，图6直观的显示了某个优化方案的优化目标值。表3是优化结果明细表，可按表3的第2行到5行的数据调整供应商的数量和销售商的数量，从而对供应链结构进行有效优化。

图5 优化运行界面

图6 供应链库存成本优化目标值

表3 最优目标值及优化变量配置

5 结论

本文的供应链结构优化研究是从供应链核心企业的总库存成本最小这个目标出发，研究如何确定上游供应商的数量和下游销售商的数量。首先利用Witness仿真软件建立需求拉动式的供应链仿真模型，然后将供应链的供应商数量和销售商数量设置为变量，核心企业的总库存成本为优化目标，利用模拟退火算法进行优化，最终得到供应链总成本取得最小值时，供应商和销售商的数量配置方案，借此配置方案，供应链核心企业可以调整上游供应商的数量和下游销售商的数量，以实现对供应链结构的合理优化。本文的研究方法对现实中供应链核心企业调整供应链结构有指导意义。