EGM2008辅助的GPS高程转换方法应用分析

王正亮薛荣军南 城杨 军孙 哲

(江苏省水文地质海洋地质勘查院,江苏 淮安223001)

0 引 言

现阶段我国正大力推进实施“一带一路”和“走出去”战略,国内很多工程企事业单位纷纷走向国外开拓国际市场,承担了很多大型基础设施建设工程。在这类工程建设施工过程中,水准测量仍然是获取正常高的主要手段。但水准测量工作强度高、效率低,国外基础控制相对落后、作业距离长,多数情况下缺少检核条件。应用GNSS水准高程测量技术是成为替代常规水准测量的重要途径。

本文选择国外某测区内GPS/水准数据进行常规拟合和EGM2008全球重力场模型辅助条件下的高程拟合,经比较验证表明,重力场模型辅助的高程拟合方法获取的高程精度和可靠性可大幅提升。

1 原理与方法

GPS测量直接获得的是以WGS-84椭球面为基准面的大地高H,而水准测量是以似大地水准面为基准面的正常高h,两者转换关系可表示为:

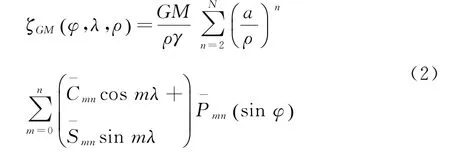
式(1)中ζ为似大地水准面到参考椭球面的距离,称为高程异常。利用重力场模型计算GPS点的模型高程异常,根据Bruns公式,地球表面上任意点的模型高程异常可由式(2)获得[1]:式(2)中:G为万有引力常数,M为地球质量,ρ、φ、λ为计算点的地心向径、地心纬度和地心经度,γ为计算点的正常重力平均值,a为参考椭球的长半轴。为完全规格化的正常位球谐系数,为完全规格化的Legendre函数,N为地球重力场模型展开的最高阶数。

利用测区内GPS/水准点数据计算高程异常值ζ',计算模型高程异常的残差值Δζ,可表示为:

利用已知高程点的模型高程异常残差值,拟合出GPS网内未进行过常规水准联测点上的模型高程异常残差值Δζi,并利用残差值对这些点上由EGM2008重力模型所计算出的高程异常值ζGM进行改正[2],最后得到经过改正后的异常值ζi=ζGM+Δζi,则式(1)相应改为:

2 实例与精度评定

2.1 拟合模型设计

模型一:二次曲面拟合。选取二次多项式曲面模型直接对高程异常ζ进行拟合,根据最小二乘原理求取模型转换参数。

模型二:三次曲面拟合。选取三次多项式曲面模型直接对高程异常ζ进行拟合,根据最小二乘原理求取模型转换参数。

模型三:EGM2008+三次曲面拟合。利用EGM2008模型求取每点高程异常,使用式(3)计算残余高程异常,使用三次曲面模型拟合残余高程异常,最小二乘法确立模型参数。根据残余高程异常模型计算模型高程异常改正值,综合EGM2008模型异常值将大地高转换为正常高(其中EGM2008模型分辨率为5'×5')。

2.2 实例概述

新建某地标轨铁路测区大部分属高原地形,平均海拔1 500 m。线路位于E36°11'08″～36°53'07″,S1°08'43″～1°20'53″之间,控制网呈带状,用控制网联测线路一端的部分高程点,进行三维空间约束平差,获取 WGS-84坐标系下的大地坐标和大地高。同期进行四等水准测量,所有点经粗差探测后均不含粗差。选取平坦地区和山地地区两个测段使用3种方案进行拟合计算,用水准数据作为检核,对比3种方案的拟合效果。

测段一总长约38 km,沿线区域地势平坦,该测段属平坦高原。共施测26个GPS/水准点,选取均匀分布的16个点作为拟合点,剩余10个点作为检核点(图1)。

测段二总长约41 km,沿线区域地势起伏,该测段属山地。共施测27个GPS/水准点,选取均匀分布的15个点作为拟合点,剩余12个点作为检核点,如下所示(图2)。

图1 平坦地区点位分布

图2 山地地区点位分布

2.3 模型结果分析

三种模型拟合结果如下所示(表1—4)。

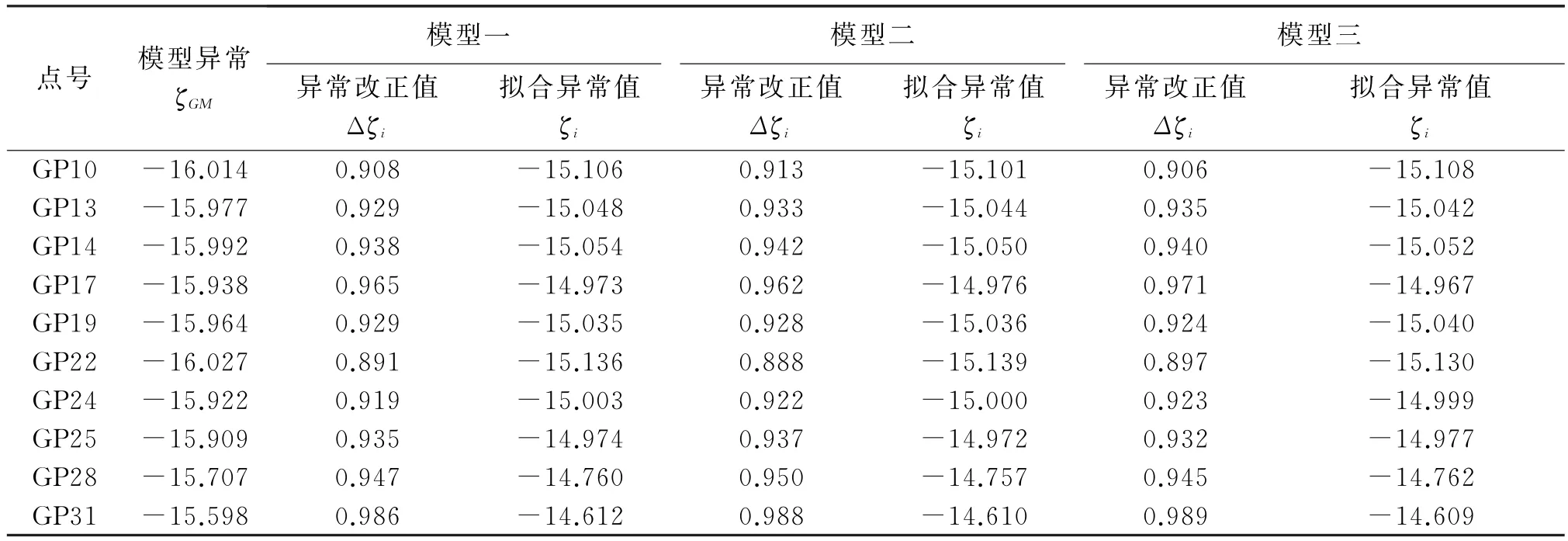
表1 测段一高程异常拟合值/m

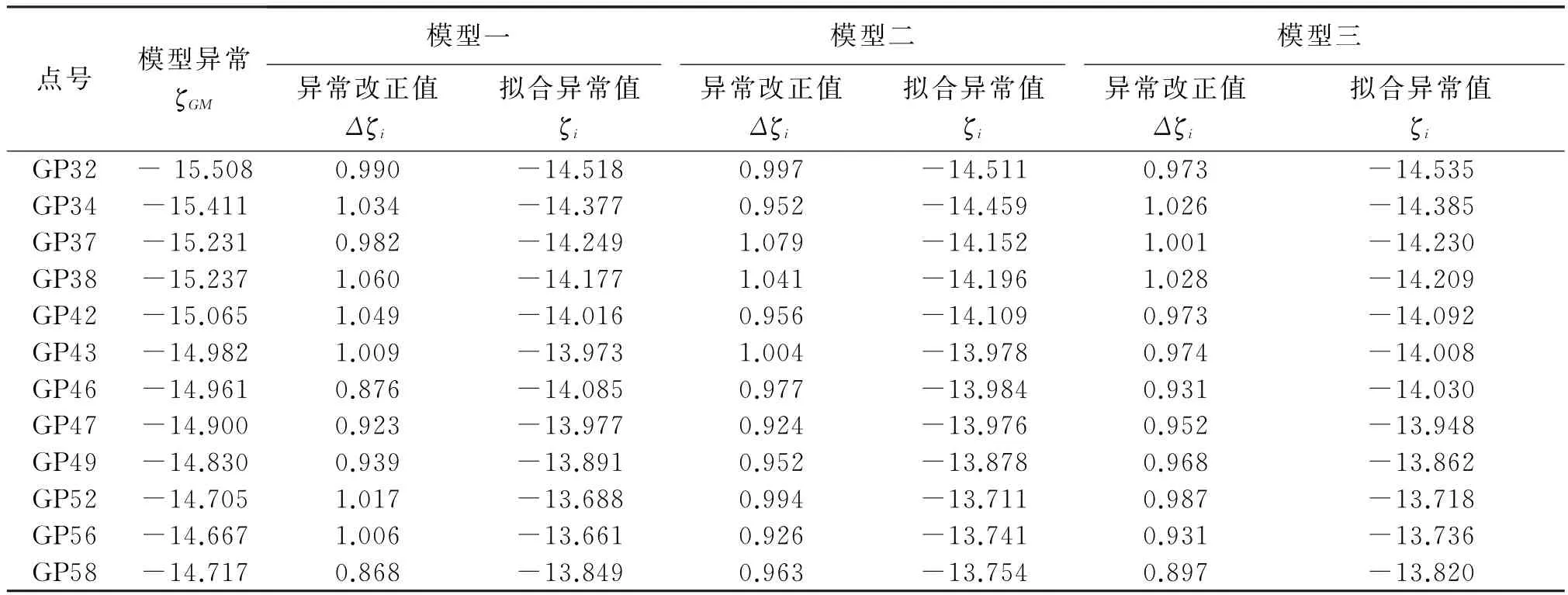
表2 测段二高程异常拟合值/m

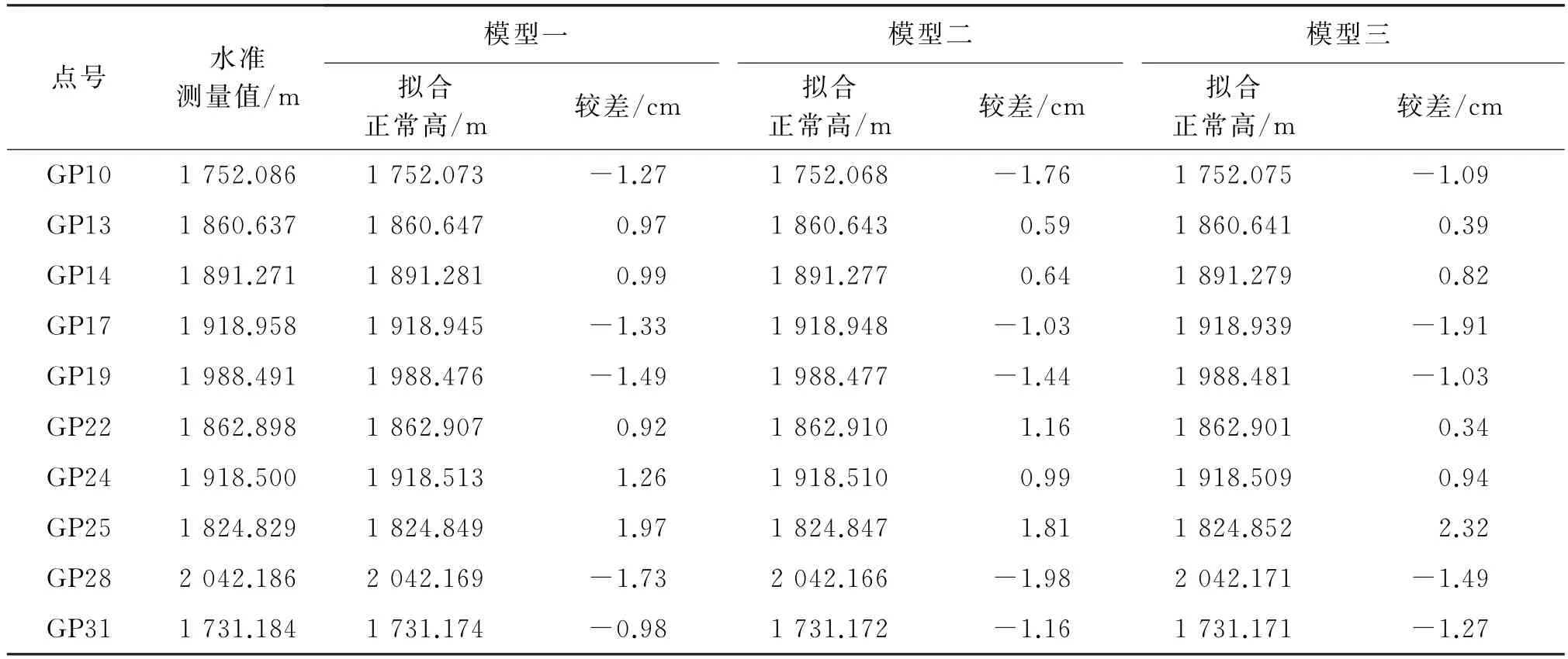
表3 测段一拟合较差表

表4 测段二拟合较差表

对上述3种拟合模型计算结果使用式(5)进行内外符合精度的评定。内符合精度反映了利用已知点所建拟合模型的质量,外符合精度反映了利用所建模型求解检核点高程异常的整体精度[3-4]。

式(5)中,v i为该点的较差值,n为参与计算点的个数。各模型内外符合精度统计如下所示(表5—6)。

从表5-6中内、外符合精度统计分析,3种模型拟合精度在平坦测区均能达到四等水准要求;在山地测区,模型三在尽可能增加均匀分布的拟合点数量或者分区拟合计算情况下也能达到四等水准精度。本例的拟合精度能满足本次铁路工程中地形图测绘、铁路定测等各项精度要求。

表5 测段一拟合模型精度统计/cm

表6 测段二拟合模型精度统计/cm

3 结 语

(1)基于EGM2008重力场模型的三次曲面GPS高程拟合,其精度优于单纯数学模型中的二次、三次曲面模型拟合,对于地形起伏较大的山地测区,拟合精度明显改善,平坦测区略优。利用EGM2008模型辅助的GPS测量进行高程拟合获取正常高能满足常规水准测量要求。

(2)EGM2008重力场模型拟合基于控制点的大地坐标和大地高。前期GPS网形设计、观测精度及平差计算至关重要。若使用较高分辨率的重力场模型拟合效果将更优[5-6]。