材料构型力驱动的复合型疲劳裂纹扩展行为研究
武志宏,王芳文,刘冉,李群
(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.西安交通大学航天航空学院,710049,西安)
在材料的实际使用过程中,大部分零部件承受的载荷是周期性变化的,而这些零部件大部分又是由于疲劳问题而失效的[1]。疲劳断裂是指裂纹在周期性扰动载荷的作用下萌生并扩展而导致的零部件破坏现象,普遍存在于机械、航空航天、海洋平台以及交通运输等领域中。因此,研究材料的疲劳失效问题具有重要的理论价值和工程意义[1-7]。目前,对于Ⅰ型疲劳裂纹在弹性应力下的扩展问题已经研究得相对比较成熟,形成了以Paris公式为代表的经验公式,建立起了应力强度因子和疲劳裂纹扩展速率之间的关系[2],并且得到了广泛的应用。但是在实际工程中,由于载荷不对称或材料各向异性等原因,结构中的裂纹通常处在组合应力场的作用下,裂尖附近的应力场表现出复合型场的特点。因此,复合型裂纹大量存在,其中又以Ⅰ-Ⅱ复合型裂纹最常见。
对于复合型疲劳裂纹扩展的研究,国内外学者主要通过断裂力学理论来解释和描述其规律[8-16]。Tanaka等釆用有效应力强度因子ΔKeff代替Paris公式中的应力强度因子,对Paris公式进行了修正[8];Hussain等将Griffith裂纹理论用于Ⅰ型疲劳裂纹的能量平衡原理并推广到复合型疲劳裂纹扩展的研究中,提出了最大能量释放率准则[10];Erdogan和Sih提出了最大切向应力准则,并将其成功应用于复合型加载条件下斜裂纹问题的研究[11];Sih等基于裂尖区域的应变能密度场,提出了应变能密度因子S的概念,并提出了最小应变能密度因子准则[12]。基于上述理论,目前一些主流的疲劳分析软件(如FE-safe、Ncode、FRANC3D)在处理裂纹扩展问题时,都是基于Paris等线弹性断裂力学理论。在对裂纹方向进行判定时,也是依据最大切向应力、最小应变能密度及最大能量释放率等参数。
在这些判定准则中,有效应力强度因子ΔKeff仅可以用来预测裂纹萌生或者起裂,但无法预测扩展方向。最大切向应力准则和最小应变能密度因子准则在预测裂纹扩展时,涉及最大切向应力和最小应变能密度,这两个参数在计算时需要选取一个标定距离,称为临界距离或特征长度[11-12],标定距离是决定最大切向应力准则以及最小应变能密度因子准则预测结果可靠性的重要因素。为此,在过去几十年中,研究人员试图提出各种模型来计算不同的脆性和准脆性材料的临界距离[17-19]。此外,应力强度因子、能量释放率更多地用于线弹性材料和小变形问题,在弹塑性、界面以及多场耦合等复杂或者多裂纹干涉问题中不易应用。
另一方面,材料构型力断裂准则能够准确地描述复合型裂纹扩展,不仅可以判断裂纹起裂条件,还可以预测裂纹扩展方向,并且在计算过程中不会受到标定距离的影响,也不需要考虑裂尖的奇异性。材料构型力是基于能量法提出的,可以反映疲劳破坏机理上的变化,并且能处理弹塑性、界面以及多场耦合等复杂问题。近年来,许多学者围绕材料构型力断裂准则做了大量工作[20-25],取得了诸多进展。Guo和Li采用材料构型力断裂准则对复合型裂纹扩展做了数值模拟研究,结果显示,构型力失效准则能够很好地预测各种形式的复合型裂纹扩展路径[21];古斌等利用构型力断裂准则对裂纹和夹杂(圆孔、软夹杂、硬夹杂)干涉问题进行了有限元分析,发现裂纹的扩展方向与裂纹和夹杂的相对位置以及夹杂的类型密切相关[22];Wang等利用构型力的M积分作为疲劳损伤的驱动力,研究了两个孔洞在循环拉伸载荷下的疲劳裂纹扩展特性,发现裂纹与孔洞汇合时M值存在明显的跳跃特性[23]。因此,材料构型力学能够准确地描述复杂裂纹的演化形式,对研究复合型疲劳裂纹扩展问题具有重要意义。
本文以材料构型力断裂准则为基础,提出了一种用于预测复合型疲劳裂纹扩展的模型,该模型不仅适用于纯Ⅰ型疲劳裂纹扩展,也适用于复合型疲劳裂纹扩展;通过有限元数值计算方法实现了疲劳裂纹扩展过程,并结合试验验证了该模型的有效性和可靠性;通过两个典型的复合型疲劳问题,预测了裂纹扩展路径和扩展寿命,以期为实际工程中材料的疲劳失效评估提供新的思路。
1 复合型疲劳裂纹扩展模型
1.1 材料构型力的定义
构型力理论的基础可追溯到Eshelby定义的能量动量张量概念[20]。经典力学建立在欧拉物理空间,力的概念直接与质量相关,涉及带有质量的物体的平衡和运动;构型力则是定义在奇点上,和给定系统的总能量的改变有关,而总能量的改变又是由该系统构型的改变引起的(即缺陷演化)。
Eshelby构型应力张量可以通过拉格朗日密度函数Λ在材料空间(初始构型)的梯度运算得到,即
(1)
式中:W表示应变能密度;-(W),i表示应变能密度W对xi方向的偏导;(∂W/∂xi)expl表示应变能密度对坐标xi的显式偏导;σkj表示应力张量;uk,ji表示位移uk对坐标xj和xi两次求导。
Eshelby构型应力bji定义为
bji=Wδji-σjkuk,i
(2)
式中:δji表示Kronecker张量,当i=j时,δji=1,i≠j时,δji=0;uk,i表示位移uk对坐标xi的求导量。
同时,定义构型应力所表征的材料缺陷源即材料构型力(后文简称构型力)为
(3)
式中:Ci表示应变能密度W沿着xi方向的显式偏导。构型力是材料损伤演化的驱动力,可以作为裂纹扩展的驱动力,它表征了奇点沿xi方向平移时的能量释放率,见图1。
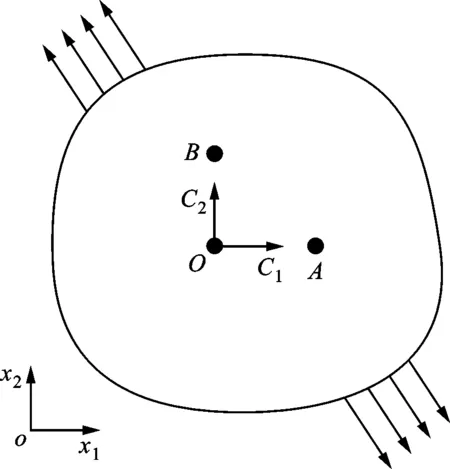
O:物理奇点;A:奇点O沿x1方向平移后的位置;B:奇点O沿x2方向平移后的位置图1 材料缺陷构型力
根据方程(1),Eshelby构型应力和构型力之间满足平衡方程
bji,j+Ci=0
(4)
1.2 材料构型力的复合型疲劳裂纹扩展模型
1.2.1 疲劳裂纹扩展模型 在实际工程中,由于载荷的不对称分布以及材料的各向异性等原因,结构中的裂纹通常处在组合应力场的作用下,使得裂尖附近的应力场呈现出复合型的特点,复合型裂纹的扩展路径会偏离初始裂纹的方向。对于复合型裂纹扩展的研究,无法直接应用已有的Paris公式,需要建立能准确表征复合型裂纹扩展规律的模型,而以构型力理论为基础的断裂准则满足了这一要求。本文基于构型力的疲劳裂纹扩展准则如图2所示,其中,x和y方向分别对应图1中的x1和x2方向。
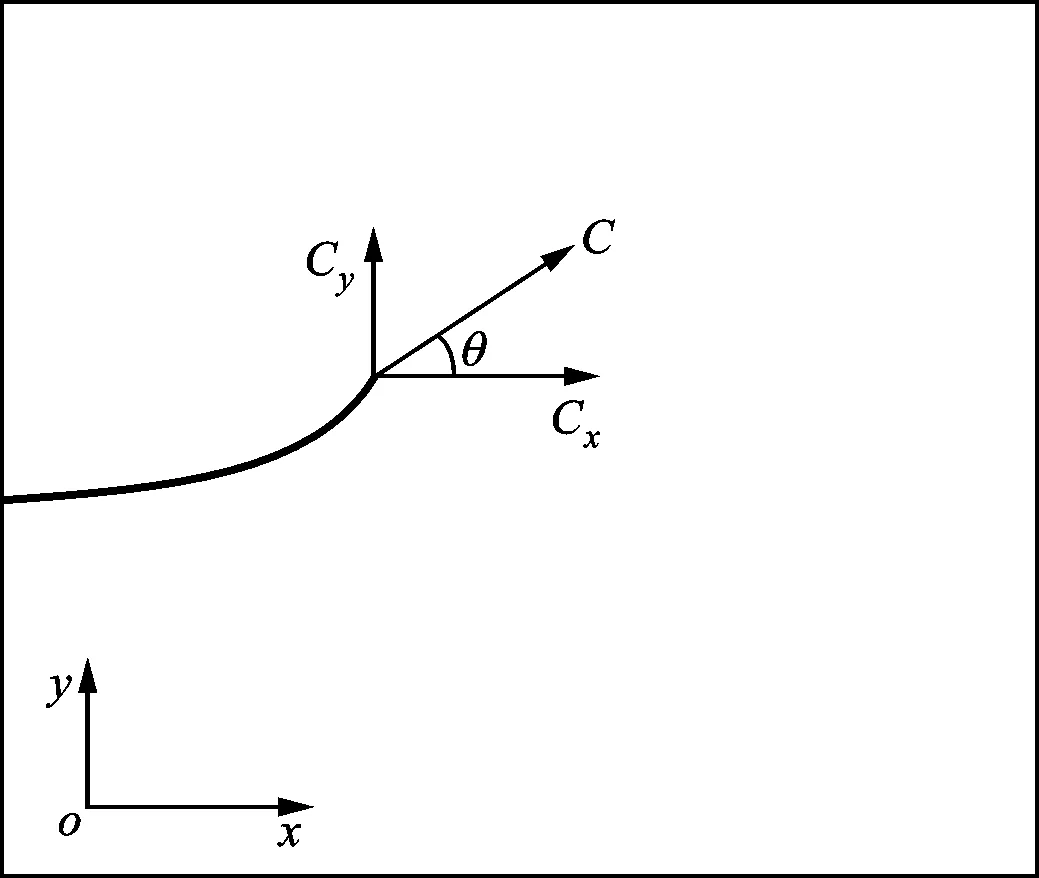
图2 疲劳裂纹扩展准则
构型力疲劳裂纹扩展准则的基本假设如下。
(1)疲劳裂纹起裂的判定。当构型力大于临界构型力时,疲劳裂纹开始扩展,即
(5)
式中:C为构型合力;Cth为临界构型力,是材料常数,与裂纹尺寸和载荷条件无关。
(2)疲劳裂纹扩展方向的判定。裂纹扩展发生在初始裂尖并沿着构型合力的方向,偏转角为
(6)
(3)疲劳寿命的预测。本文采用构型力作为疲劳裂纹扩展的控制参量,提出构型力复合型疲劳裂纹扩展模型
(7)
式中:a为裂纹长度;N为疲劳载荷循环次数;B和P为材料常数,与载荷条件和裂纹尺寸无关;ΔC为构型力因子幅。需要注意的是,该模型只适用于疲劳裂纹扩展的Ⅱ阶段,即稳定阶段。
整个疲劳裂纹扩展过程见图3。基于构型力的复合型疲劳裂纹扩展模型用构型力因子幅作为裂纹扩展的控制因素,不仅能在机理上真实反映复合型疲劳裂纹扩展的规律,还能准确预测裂纹扩展的方向,预防材料失效,避免事故发生。
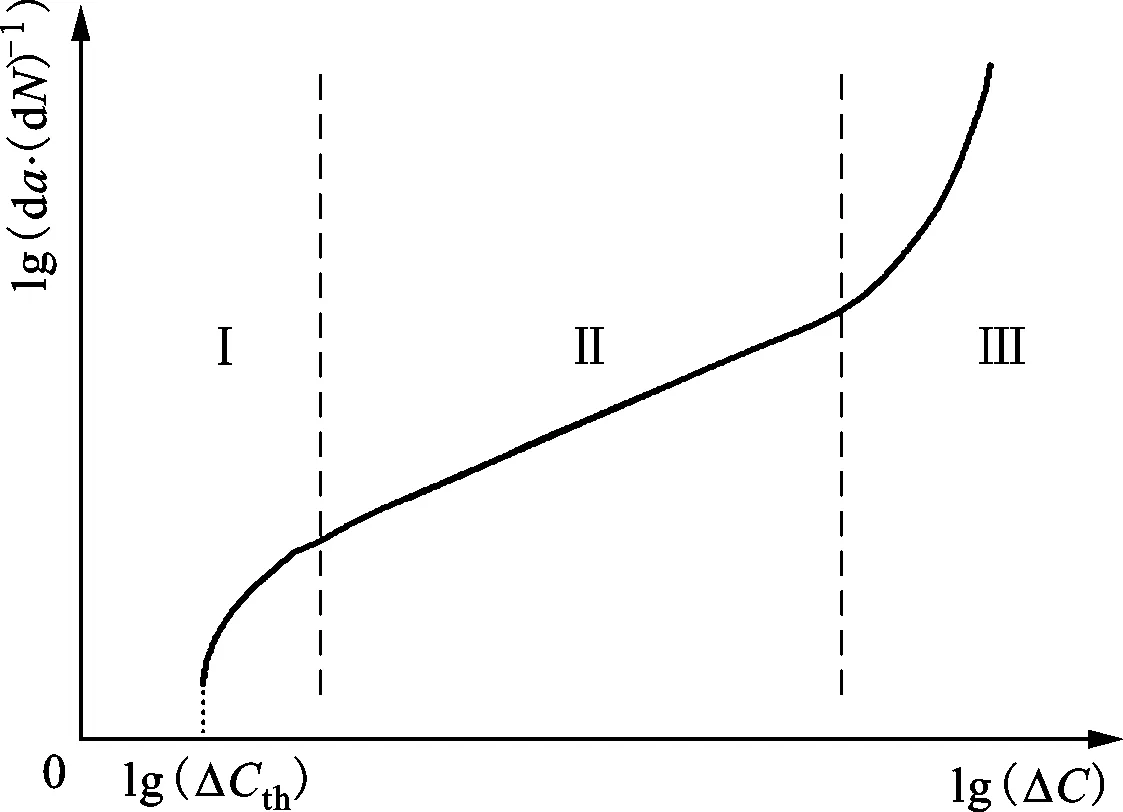
图3 疲劳裂纹扩展曲线
1.2.2 构型力模型和Paris模型的比较 对于疲劳裂纹扩展问题的研究,主要还是围绕线弹性断裂力学理论。1963年,Paris等学者建立了疲劳裂纹扩展速率da/dN和应力强度因子幅ΔK之间的关系,奠定了疲劳断裂力学的理论基础[2]。对于线弹性材料问题,应力强度因子K与构型力分量Cx具有内在联系,其关系式为
(8)
式中:KⅠ为Ⅰ型裂纹的应力强度因子;KⅡ为Ⅱ型裂纹的应力强度因子;KⅢ为Ⅲ型裂纹的应力强度因子;E为弹性模量;ν为泊松比。
但是需要指出的是,此关联性仅适用于线弹性材料。对于其他问题,例如弹塑性、界面以及多场耦合等问题,应力强度因子K无法预测疲劳裂纹扩展,具有诸多局限性。本文提出的疲劳扩展准则,不仅考虑了Cx的贡献,更重要的是也考虑了Cy的贡献。
构型力疲劳裂纹扩展模型的优势主要有:①无需定义裂尖的断裂进行区;②可以同时判断起裂条件和预测裂纹扩展方向;③不仅适用于线弹性材料,也适用于弹塑性、界面耦合及多裂纹等复杂问题,特别是对于预测复合型裂纹以及缺陷干涉对于裂纹扩展方向的改变规律,具有一定优势。
1.2.3 临界构型力的测量 在疲劳裂纹扩展的过程中,临界构型力Cth是判断裂纹是否起裂的重要材料参数,且与外界载荷及构件尺寸无关,主要通过试验手段测量获得[26-27],而临界构型力Cth的值可定义为材料失效时刻的构型力。
从式(2)和式(3)可以看出,在测量构型力的试验中,关键是要获得平面内用于计算Eshelby构型应力的相关分量,例如应变能密度、应力以及位移梯度等。测试件变形的位移通过数字图像相关技术获取:在试验过程中,采集测试件的图像,将在未变形状态下采集的图像的作为参考图像,并在图像中生成许多像素子集,与变形发生后采集的图像进行对比,寻找每个像素子集区块的移动,进而得到测试件在失效时,图像中各个区块的位移,根据位移和应变的关系,即可得到测试件表面各个分量的应变场。通过材料的本构方程、几何方程和平衡方程等,最终计算得到临界构型力Cth。
2 数值计算方法
目前,对于疲劳裂纹扩展问题的研究主要集中在试验研究和数值计算两个方面[28-35]。本文采用数值计算方法,根据构型力复合型疲劳裂纹扩展模型并结合构型力有限元计算方法,计算了材料疲劳裂纹的扩展速率、路径以及寿命,其流程图见图4。
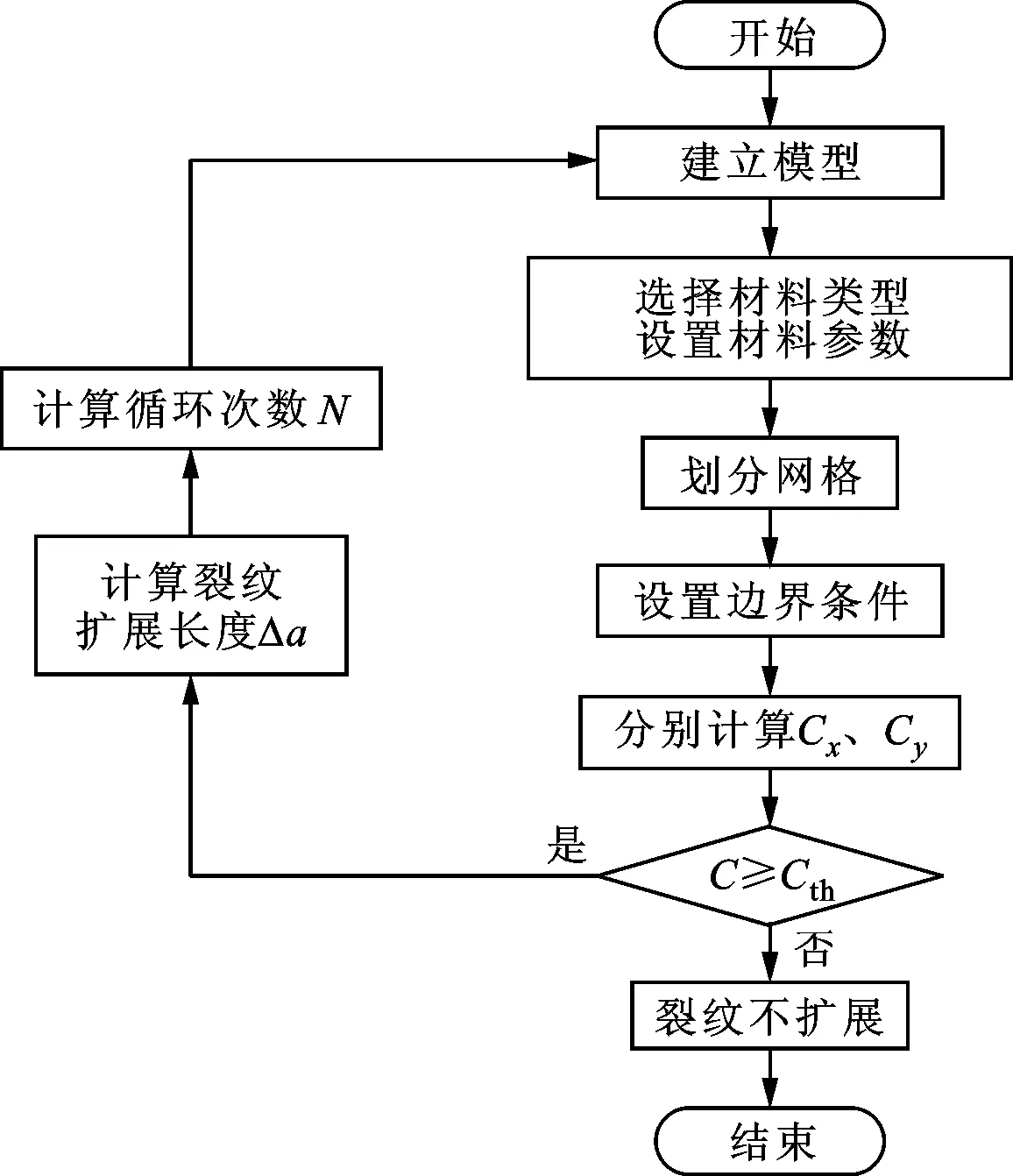
图4 数值计算流程图
首先,根据结构几何尺寸和初始裂纹情况建立模型,设置材料参数,并完成网格划分。然后,对模型施加相应的载荷和边界条件,计算得到x、y两个方向上的构型力分量Cx、Cy,并根据两个分量确定构型力合力C,比较构型合力C与临界构型力Cth,判断疲劳裂纹是否发生扩展:若C大于等于Cth,则裂纹发生扩展;若C小于Cth,则表示裂纹扩展驱动力不足以克服裂纹扩展阻力,裂纹不发生扩展,跳出循环。若裂纹发生扩展,扩展方向θ依据公式(6)得出,并假定裂纹向前扩展一个步长Δa;然后,根据复合型疲劳裂纹扩展模型(7)得到对应的循环次数N,完成一次裂纹扩展过程(在选取裂纹扩展步长Δa时,应保证整个裂纹扩展过程是稳定的,并且在确保整个裂纹扩展轨迹保持不变的前提下,尽可能地选择较大的扩展步长,减少计算量,并对当前扩展步长Δa的收敛性进行验证);最后,根据新裂纹的扩展方向和尺寸,生成新的有限元模型,依次循环,最终获得裂纹扩展寿命曲线(a-N曲线)以及扩展路径。
为了提高计算效率,对有限元计算过程做了优化处理:在重新划分网格时,只对裂尖以及附近区域做局部加密的自由网格处理,而对裂纹远端的网格采用固定网格的形式,不参与网格重构。
3 疲劳裂纹扩展数值计算与结果讨论
3.1 试验验证
近期,黄学伟等围绕低周疲劳特性,开展了对复合型疲劳裂纹扩展的研究工作[13-14]。本文参考文献[13]的基于标准紧凑拉伸(compact tension,CT)试样(Ⅰ型)以及改进CT试样(复合型)的疲劳裂纹扩展试验,对提出的材料构型力复合型疲劳裂纹扩展模型的可靠性进行了验证。试样材料为CrNi2MoV钢,尺寸见图5,l0=40 mm,厚度l1=5 mm,初始裂纹长度a0=10 mm。此外,为研究复合型疲劳裂纹扩展,在标准CT试样初始裂纹末端加工一个偏离水平方向(α=60°)、长度a1=2 mm的斜裂纹。施加载荷Fmax=4 KN,应力比R=0.1。
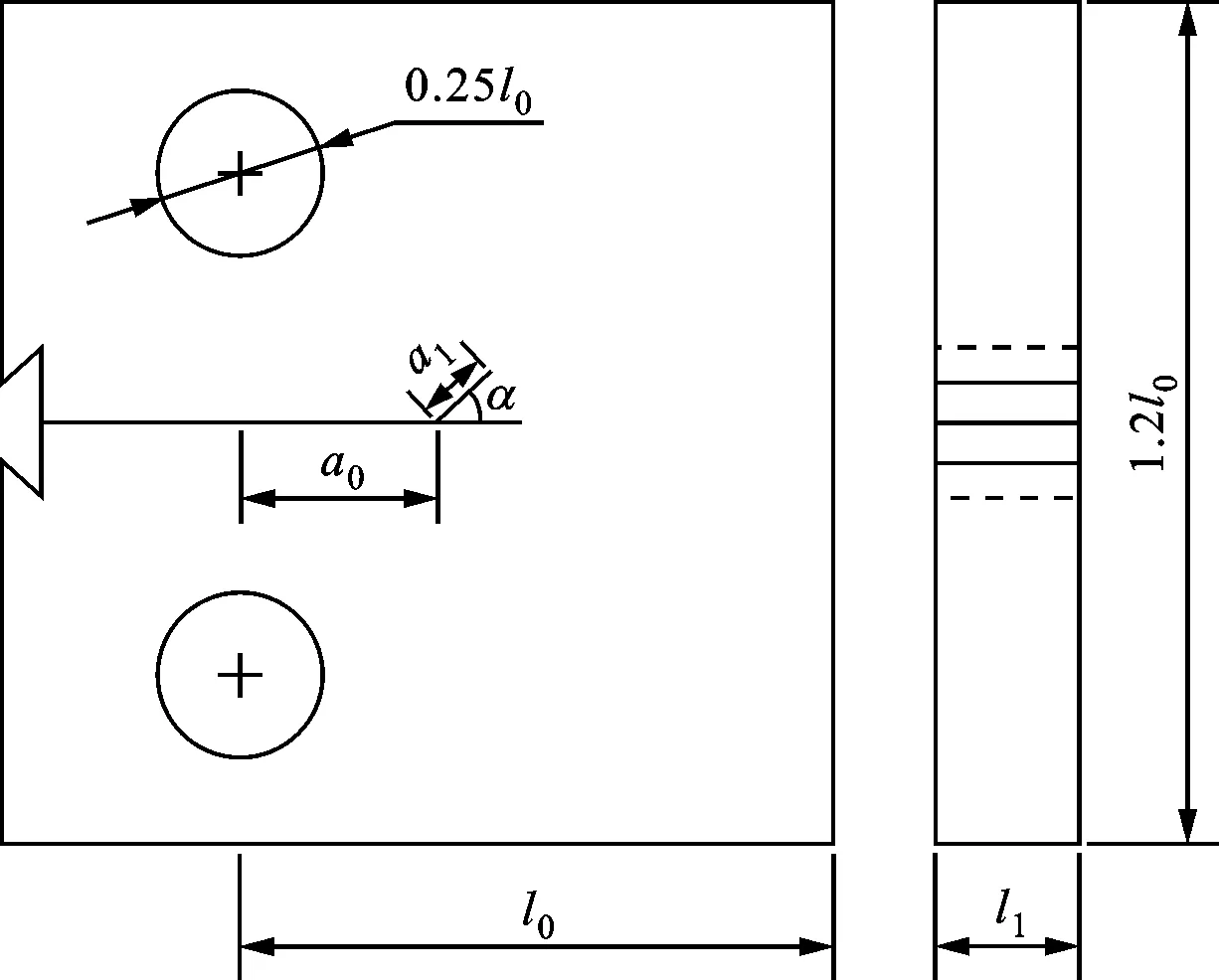
图5 CT试样尺寸示意图
通过试验,文献[13]计算得到Paris公式参数C和m分别为1.11×10-8和2.71。对于线弹性材料中含有Ⅰ型裂纹的情况,构型力Cx等效于能量释放率。通过构型力与应力强度因子之间的关系,结合公式(7),可得构型力复合型疲劳裂纹模型中的常数项,分别为:B=0.186 5,p=1.355。因此,构型力复合型疲劳裂纹扩展模型为
(9)
将该模型与文献[13]的试验结果进行对比,结果如下。
(1)直裂纹(Ⅰ型)疲劳扩展结果。有限元计算过程采用线弹性材料本构,弹性模量E=215 GPa,泊松比ν=0.3。在计算过程中,施加的载荷Fmax使得裂尖的构型合力始终大于临界构型力Cth,所以,不需要判定临界载荷。计算Ⅰ型疲劳裂纹长度随循环次数的变化情况,即a-N曲线,并对比文献[13]的CT试样直裂纹疲劳试验结果,结果见图6。

图6 CT试样的直裂纹a-N曲线
从图6中可以看出,3种情况得到的a-N曲线趋势基本一致。对于最终寿命(循环次数)而言,基于构型力因子幅的有限元结果和试验误差只有3.24%。由此可见,基于构型力的疲劳裂纹扩展模型能够很好的模拟Ⅰ型疲劳裂纹的扩展状况,具有良好的精度。
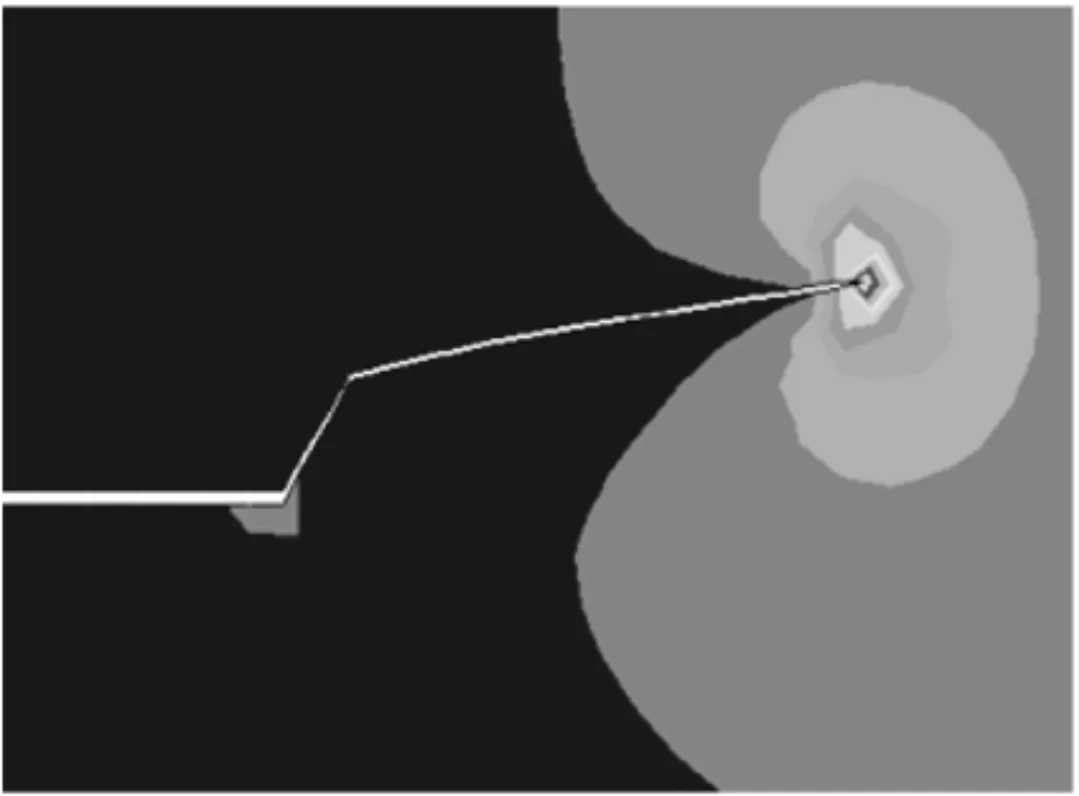
(a)数值计算结果

(b)文献[13]试验结果图7 CT试样的复合型疲劳裂纹扩展路径
(2)复合型疲劳裂纹扩展结果。对于复合型疲劳裂纹扩展,文献[13]利用CT改进试样对复合型疲劳裂纹进行了试验研究,并定义复合型裂纹长度为裂纹曲线的实际弧长度。本小节将构型力复合型疲劳裂纹扩展模型计算得到的数值结果和文献[13]的试验结果进行对比验证,结果见图7,可以看出:疲劳裂纹从线切割预制的裂纹根部开始扩展,拐折一定角度后沿着Ⅰ型裂纹方向扩展,数值计算预测的复合型裂纹扩展趋势和试验结果基本一致。
根据式(9)给出的复合型疲劳裂纹扩展规律,合理选择扩展步长Δa,采用跳跃计算得了到a-N曲线,该曲线与文献[13]试验结果的对比见图8,可以看出:数值计算和试验结果的误差为7.29%,且两者裂纹扩展速率趋势基本一致。需要注意的是:①裂纹长度是指从初始裂纹开始扩展的裂纹长度;②为了加快裂纹萌生,文献[13]在试验过程中采用了分级加载的方式,即前104周施加较大载荷(Pmax=3 KN),104周以后施加较小载荷(Pmax=2 KN)[13],所以疲劳裂纹扩展速率在前104周较大,同样的,在数值计算的过程中也采用了分级加载的方式,以保证与试验条件完全一致。
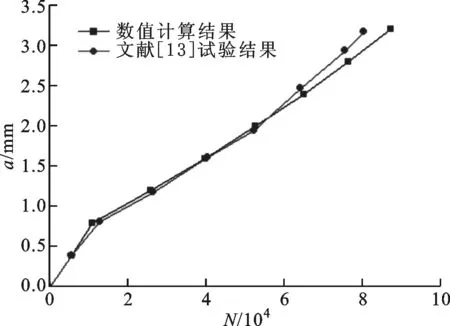
图8 CT试样复合型疲劳裂纹a-N曲线
通过上述试验,基于构型力的复合型疲劳裂纹扩展模型在预测裂纹扩展路径以及疲劳裂纹扩展寿命两方面的有效性得到了验证,可以认为:构型力复合型疲劳裂纹扩展模型是可信而且可行的。
3.2 典型的疲劳裂纹扩展分析
在材料的疲劳失效过程中,不同几何形状的构件在不同载荷的作用下,疲劳裂纹扩展往往呈现出具有复杂性和多样性的特点。如果针对每一种工况条件下的疲劳问题都通过试验手段来解决,需要花费大量时间、精力,代价极高。
采用复合型疲劳裂纹扩展模型,基于直裂纹标准试验基础,获得与之相对应的复合型裂纹模型,再结合有限元数值计算方法,可以得到任意工况条件下的疲劳裂纹扩展路径和寿命,进而对结构是否失效进行判断。平板边界斜裂纹和疲劳裂纹与孔干涉问题是典型的工程疲劳问题,因此,下文将通过构型力复合疲劳裂纹模型对其展开详细研究。
(1)平板边界斜裂纹问题。本小节的分析对象是含边界斜裂纹的矩形板。通过基于构型力的复合疲劳裂纹扩展模型计算裂纹扩展寿命,同时得到构型力在裂纹扩展过程中的变化情况,分析不同角度对裂纹疲劳寿命的影响。图9是金属板边界斜裂纹示意图,可以看出:斜裂纹存在于金属板左边界,初始长度a0=10 mm,与水平方向的夹角即偏转角为α。100 MPa的均布载荷施加于金属板的上下边界,应力比R=0.1,假设该模型处于平面应力状态,材料为CrNi2MoV钢。在数值计算过程中,α分别取值15°、30°、45°、60°、75°,观察不同角度下疲劳裂纹的扩展寿命,结果见图10,可以看出:偏转角会影响斜裂纹的扩展寿命;偏转角越小,裂纹扩展寿命越短。
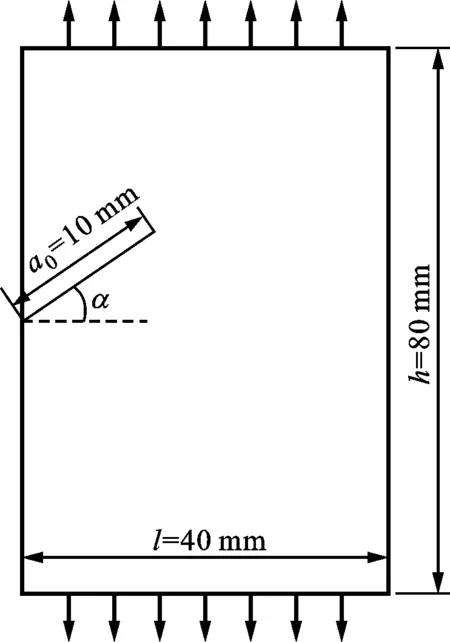
图9 金属板边界斜裂纹示意图

图10 不同偏转角下金属板边界斜裂纹的a-N曲线
同时,将不同偏转角下的裂纹扩展过程中的构型力因子幅提取出来,见图11,可以发现:在整个疲劳裂纹扩展过程中,偏转角α较小的斜裂纹的构型力因子幅较大。这是因为当偏转角α较小时,驱动裂纹扩展的能量远大于裂纹扩展的阻力,裂纹处于不稳定的状态,更加容易扩展,所以寿命越短,这与寿命预测的结果是一致的。
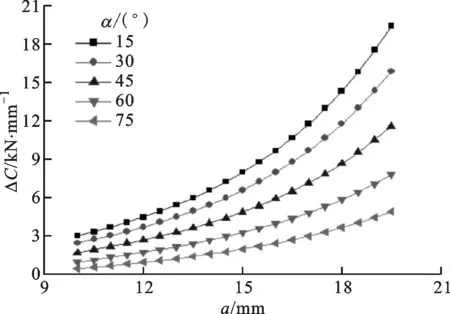
图11 不同偏转角下金属板边界斜裂纹裂尖 构型力因子幅随裂纹长度的变化
(2)疲劳裂纹与孔洞干涉问题。材料构件在实际使用过程中,常常会出现螺纹孔等孔洞特征,这些特征会对附近的疲劳裂纹产生影响,导致裂尖承受着复合型载荷,影响其扩展路径和寿命。本小节将重点考虑裂纹和圆形孔洞的干涉作用,分析其对裂纹扩展路径和寿命的影响。如图12所示,研究对象为一带边界裂纹的金属板,材料属性、边界条件以及施加载荷与平板边界斜裂纹(图9)一致,在初始裂纹的前端,有1个直径为6 mm的圆孔,圆孔中心到初始裂纹的垂直距离为d。
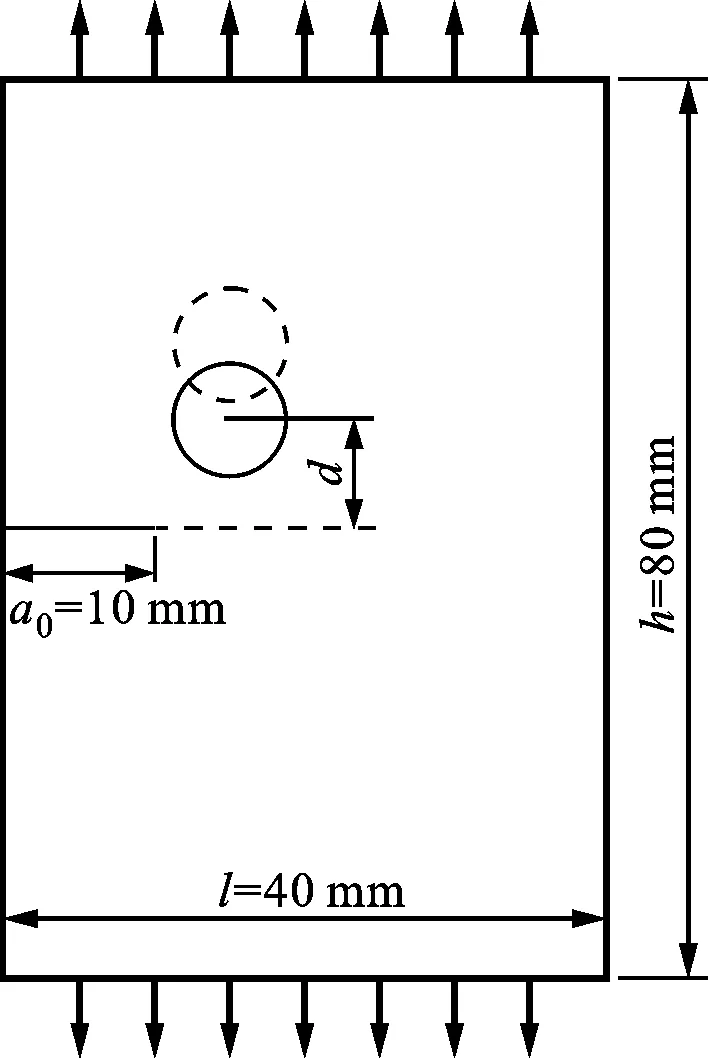
图12 含圆孔的金属板边界裂纹示意图
首先,考虑在有孔洞和无孔洞两种情况下的疲劳裂纹扩展寿命。此时,距离不变且取值d=4 mm,计算结果见图13,可以看出:孔洞的存在会在一定程度上削弱结构的疲劳裂纹扩展寿命。

图13 有孔洞和无孔洞条件下的疲劳裂纹a-N曲线
其次,研究在不同垂直距离d的条件下,孔洞对于疲劳裂纹的干涉影响。在d分别取值为4 mm、6 mm、8 mm和10 mm的4种不同情况下进行数值计算,分析在不同的裂纹和孔洞的相对位置下,裂纹扩展轨迹的变化情况,结果见图14。

(a)d=4 mm (b)d=6 mm
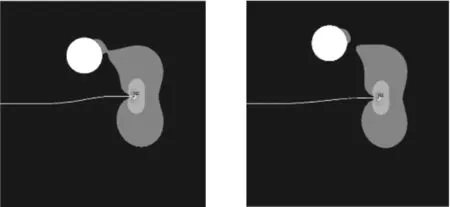
(c)d=8 mm (d)d=10 mm图14 不同垂直距离条件下的疲劳裂纹扩展路径图
由图14可以看出:当d=4 mm时,裂纹一开始扩展就受到孔洞的影响,向着孔洞的方向发生偏转,最终与孔洞聚合,裂纹停止扩展;当d=6 mm或d=8 mm时,裂纹在开始扩展时同样受到了孔洞的影响,朝着孔洞方向偏转,但是当扩展一定距离以后,孔洞对裂纹的干涉作用减弱,裂纹朝着初始裂纹正前方的方向扩展,直至断裂失效;当d=10 mm时,孔洞对裂纹的干涉作用特别微弱,裂纹只是朝着孔洞方向稍微偏折,基本沿着裂纹正前方扩展。
上述4种不同条件下的疲劳裂纹扩展寿命见图15,可以看出:当垂直距离较小时,孔洞对疲劳裂纹扩展起促进作用,裂纹扩展速率加快,寿命减短;当垂直距离较大时,孔洞对疲劳裂纹的干涉作用减弱,距离越大,干涉作用越小,寿命越长。

图15 不同垂直距离条件下的疲劳裂纹a-N曲线
裂纹扩展过程中裂尖构型力因子幅的变化情况见图16,可以看出:当d=4 mm时,裂尖的构型力在发生起裂以后迅速增大,直至发生聚合;当d=6 mm时,裂尖构型力呈现先变大再变小最后再增大的趋势,这说明此时圆孔的存在对裂纹扩展过程的某一阶段起到了抑制的作用;当d=8 mm或d=10 mm时,裂尖构型力虽然呈现出逐渐增大的趋势,但是增长幅度并没有当d=4 mm时大。因此,当裂纹和孔洞的间距处在一个恰当的距离时,裂尖构型力将一直减小,并可能小于临界构型力Cth,裂纹扩展速率可能衰减至0,并发生止裂现象。
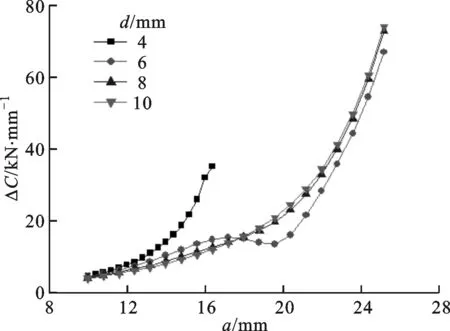
图16 不同垂直距离条件下裂尖构型力因子幅 随裂纹长度的变化趋势
4 结 论
本文结合材料构型力失效准则,提出了一种预测复合型疲劳裂纹扩展速率的模型,通过有限元方法对疲劳裂纹扩展过程进行数值实现,预测了其扩展路径及寿命,获得的主要结论如下:
(1)通过提出模型分别对Ⅰ型和复合型疲劳裂纹进行了数值计算,计算结果与试验结果基本一致,证明了提出模型的有效性和可靠性;
(2)针对不同偏转角下的复合型疲劳裂纹扩展问题,应用提出模型进行分析,得到了裂纹长度a与循环次数N之间的关系,同时获得了不同初始偏转角度下的疲劳裂纹扩展路径,可为复合型疲劳失效问题的研究提供参考;
(3)研究了疲劳裂纹和孔洞干涉问题,发现孔洞会影响疲劳裂纹扩展路径和寿命,而且在某些情况下,孔洞会减缓疲劳裂纹扩展的速率,出现止裂现象。

