地铁用电机传热特性数值模拟与实验研究
梁雪琪,罗慧强,吴一宁,曾敏
(1.西安交通大学热流科学与工程教育部重点实验室,710049,西安;2.中车永济电机有限公司,044000,山西永济)
电机在日常生活、工农业生产、航空航天等领域应用广泛。随着科技进步,很多场合需要更大功率、更紧凑的电机[1],由此导致的电机发热问题更加严重。电机内部过热会导致绝缘材料受损,进而形成短路,甚至将电机烧毁,使设备的运行具有安全隐患,同时也影响电机的使用寿命;此外,超温还会使电机内部磁性材料磁性减弱,甚至退磁[2]。因此,对电机的温度场进行探究十分必要。
电机内部的转子部分包含很多旋转部件,不易通过实验实时测量出其温度分布。另外,电机中很多实心部件的内部温度也不易测量,实施起来十分复杂。
目前,国内外专家学者主要针对发电机内某一部分,例如定子或转子等局部流场和温度场进行研究分析,忽略了换热的整体连续性;也有少部分学者对电机整体进行传热特性分析,但近似认为电机为轴向和周向对称,采用轴向1/2,周向1/6或1/12的对称模型进行数值模拟[3-8],忽略了电机中定子线圈三维弯扭、风扇叶片不对称分布的特点,以及其他不对称部件对流场的影响。本文采用电机全域模型进行数值计算,研究电机内部温度分布,并对电机进行了实验测温,还对仿真结果进行了校核。
1 模型建立
1.1 基本假设
为了便于计算,本文对电机模型做出如下简化:①假设电机的损耗在同一部件上均匀分布;②忽略电机上的螺钉、螺栓、垫片、倒角、倒圆角、电气接线盒、支撑组件、油封等对传热和流动特性影响非常小的次要零件;③将电机中球墨铸铁、钢板、碳素钢板、碳素结构钢等与纯铁相近的材料均按照纯铁的物性计算;④近似认为电机内空气物性随其温度线性变化,忽略电机内其他材料的导热系数随温度的变化;⑤假设电机已处于稳定运行状态,空气处于连续稳定的工作状态。
1.2 求解域物理模型
进行以上合理简化后的电机三维模型纵截面剖视图如图1所示,电机的几何参数见表1。电机的转速为2 014 r/min,转子周向均匀分布12个直径为25 mm的通风孔,定转子气隙厚度为1.8 mm。
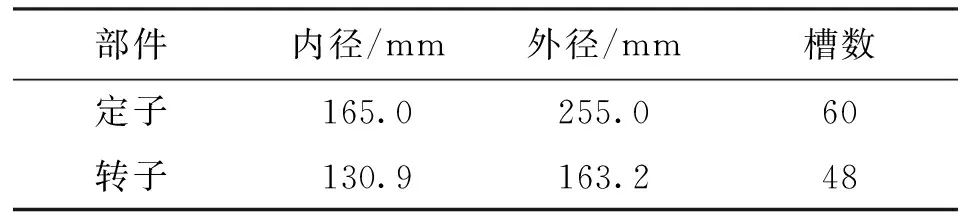
表1 电机几何参数
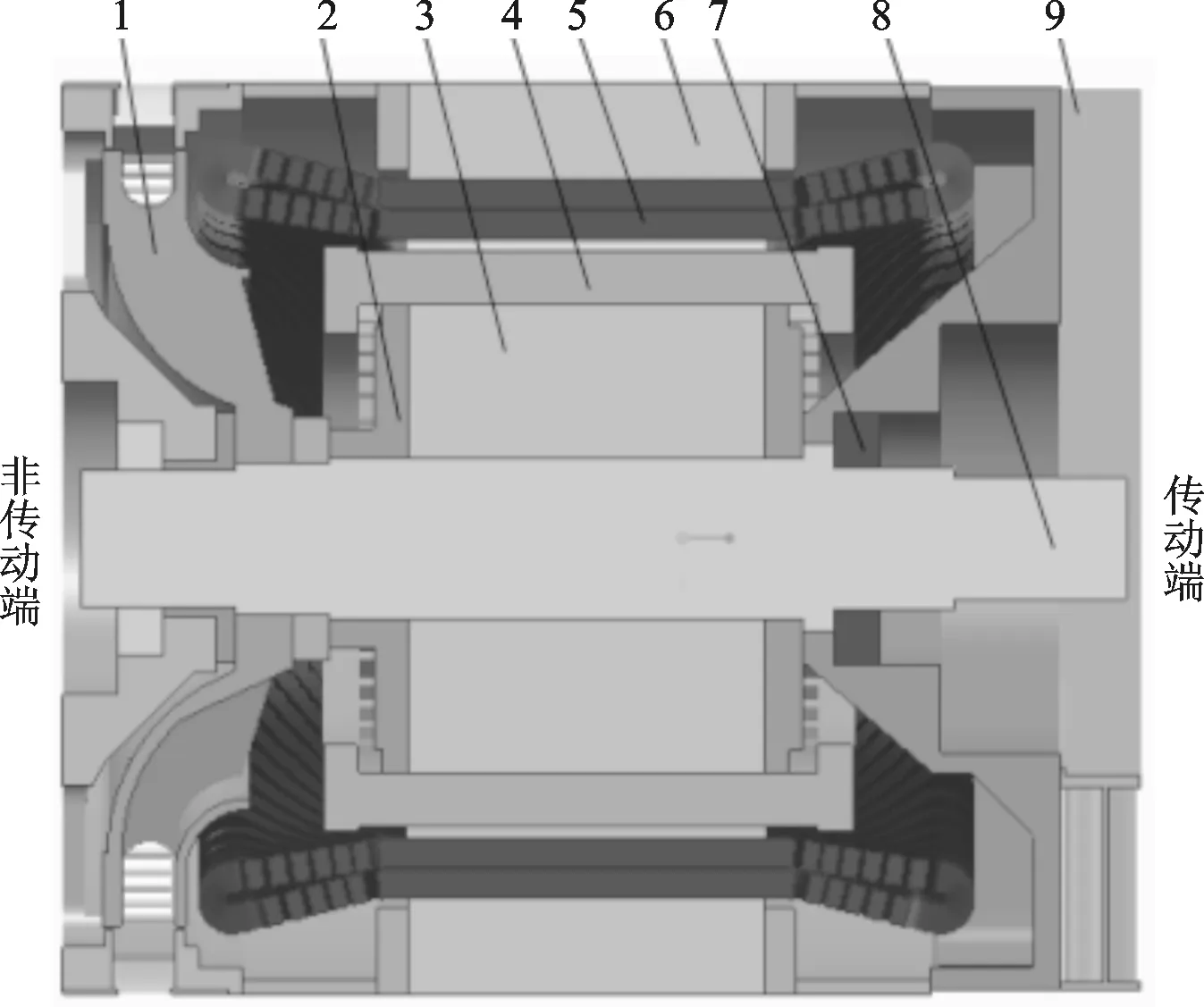
1:风扇;2:转子压板;3:转子铁心;4:转子线圈;5:定子线圈;6:定子铁心;7:轴承;8:转轴;9:入口滤尘装置图1 自通风电动机结构三维模型
电机在额定状态下运行时,所产生的铁损、铜损、杂散损耗及机械损耗如表2所示。以上各类损耗分别加载在对应部件上,其中铁耗的70%加载在定子铁心,30%加载在转子铁心,杂散损耗的50%加载在定子铁心,另外50%加载在转子铁心[9]。各相关部件的总损耗和体积损耗如表3所示。求解的物理模型包含流体域,按照多重旋转坐标系方法的要求,将流体域划分为旋转部件周围的流体域和静止部件周围的流体域两部分,如图2所示。

表2 各类损耗数值 kW

表3 电机各部件损耗分布
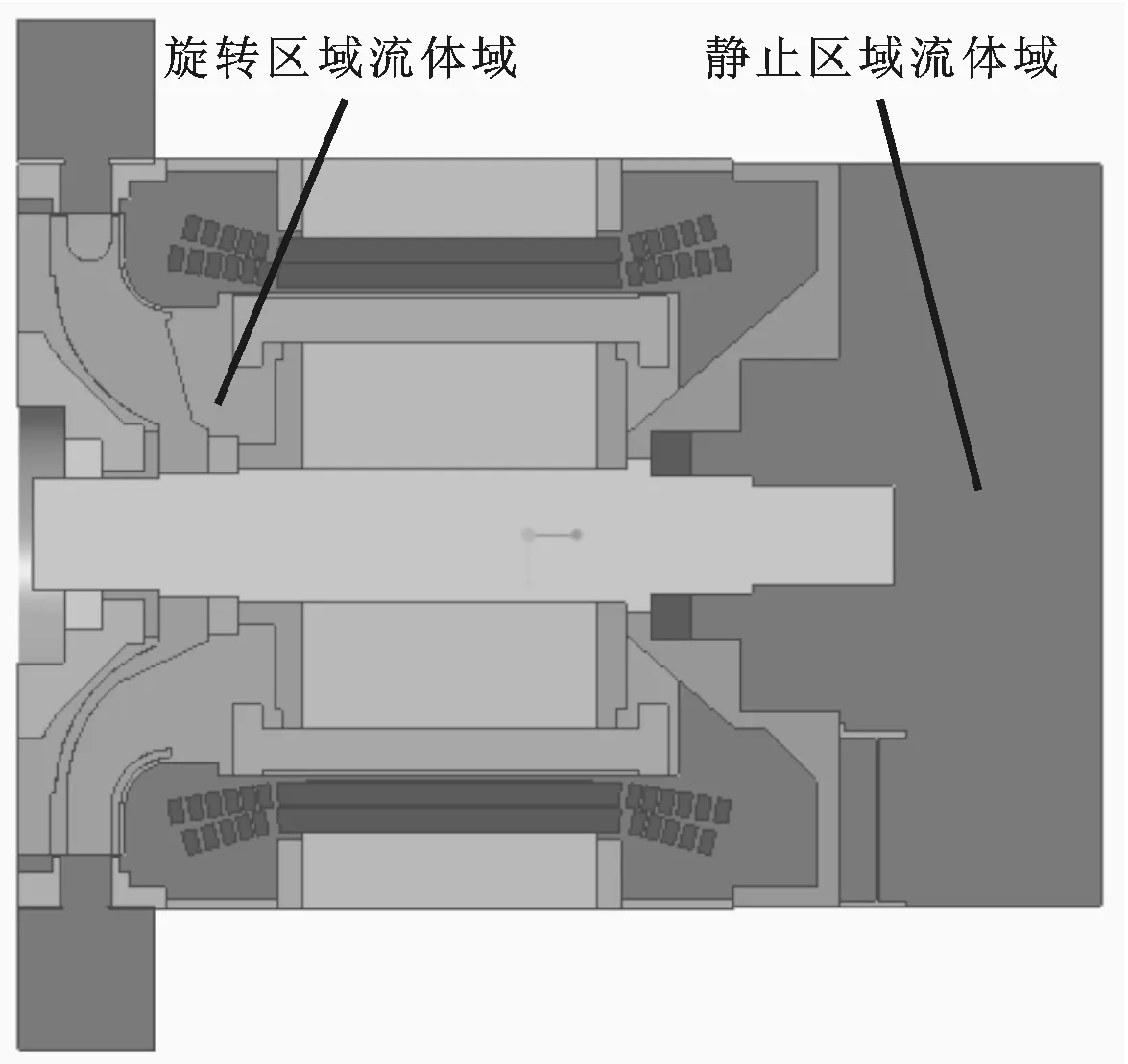
图2 求解域模型
电机运行时风扇高速转动,在电机内特别是风扇周围产生低压区,在压差驱动下,低温空气经过入口滤尘装置过滤掉灰尘颗粒后进入电机,通过定子与转子之间的气隙和转子铁心上沿圆周均匀分布的12个通风孔对电机定子、转子进行冷却,最后热风通过风扇从风罩径向的格栅流出。
1.3 数学模型
根据基本假设⑤,空气处于连续稳定的工作状态,则空气满足连续性方程
div(ρU)=0
(1)
式中U为空气的速度。
对于该稳态问题,湍流动量方程、能量方程以及标准k-ε方程可写成如下通用形式[10]
div(ρVφ)=div(Γgradφ)+S
(2)
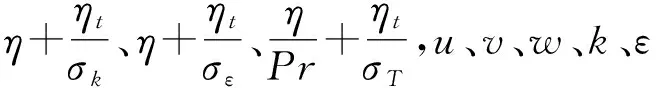
本文采用标准k-ε湍流模型计算,近壁面区域采用标准壁面函数进行处理。
1.4 边界条件
1.4.1 速度边界条件 本文研究的电机为自通风电动机,转动部件的转速决定入口和出口处的空气流速,故将入口设置为压力入口边界条件,相对压力为0;出口设置为压力出口边界条件,相对压力为0。旋转流体域和静止流体域交界面采用interior边界。流体和固体交界面采用无滑移固壁边界条件,即uair=uwall。
电机外表面设置为第三类边界条件,对于静止部件,例如定子铁心等,根据水平圆柱在空气中自然对流的特征数关联式(3)[11]及式(4),求得静止部件在空气中的自然对流换热系数h1为5.5 W/(m2·K),关联式如下所示
(3)
h=Nuλ/l
(4)
式中:l取定子铁心外径0.51 m;λ取40 ℃下的空气导热系数0.026 62 W/(m·K)。电机旋转部件包括转子铁心、转子线圈、转轴、风扇等,其中直接暴露在外部空气中的有转轴端部和轴承,外表面为在空气中的强制对流换热,文献[12]表明气体强制对流换热系数取值范围为20~100 W/(m2·K),近似取转轴和轴承外部的对流换热系数h2为80 W/(m2·K)。
1.4.2 温度边界条件 流固界面和固固界面采用热耦合边界条件[13]。出口侧流体域在轴向由于有薄片结构与空气相隔,建模中为了简化计算,将薄片结构忽略,因此流体域出口侧在轴向近似为绝热边界,即热流量q=0。
1.5 网格划分
采用Workbench中Mesh模块对图2中所示求解域进行网格划分,网格划分的基本思想是保证网格在不同零件交界面处节点对齐;由于流动比导热问题更复杂,故将流体区网格设置得较固体区更密;流体区创建边界层网格以提高流场计算准确度;对于质量较差网格,例如定子线圈等部位,进行局部面网格加密,以保证较好的网格质量。
网格划分示意图如图3所示,共2 820万个有限元体积。在Mesh模块中进行网格质量检测,检测结果表明网格的质量基本在0.45以上,网格倾斜率基本在0.75以下,一般工程问题网格质量保证在0.3以上,倾斜率保证在0.9以下即可,网格质量和倾斜率两个参数的检测结果表明网格质量较好。

图3 网格划分示意图
为了进行网格无关性验证,对求解域划分4套网格,网格数依次为1 029万、1 820万、2 820万、3 670万,在相同的边界条件下计算进口流量和热流量的变化如图4所示,根据网格无关性验证结果,本文采用2 820万网格进行数值计算。
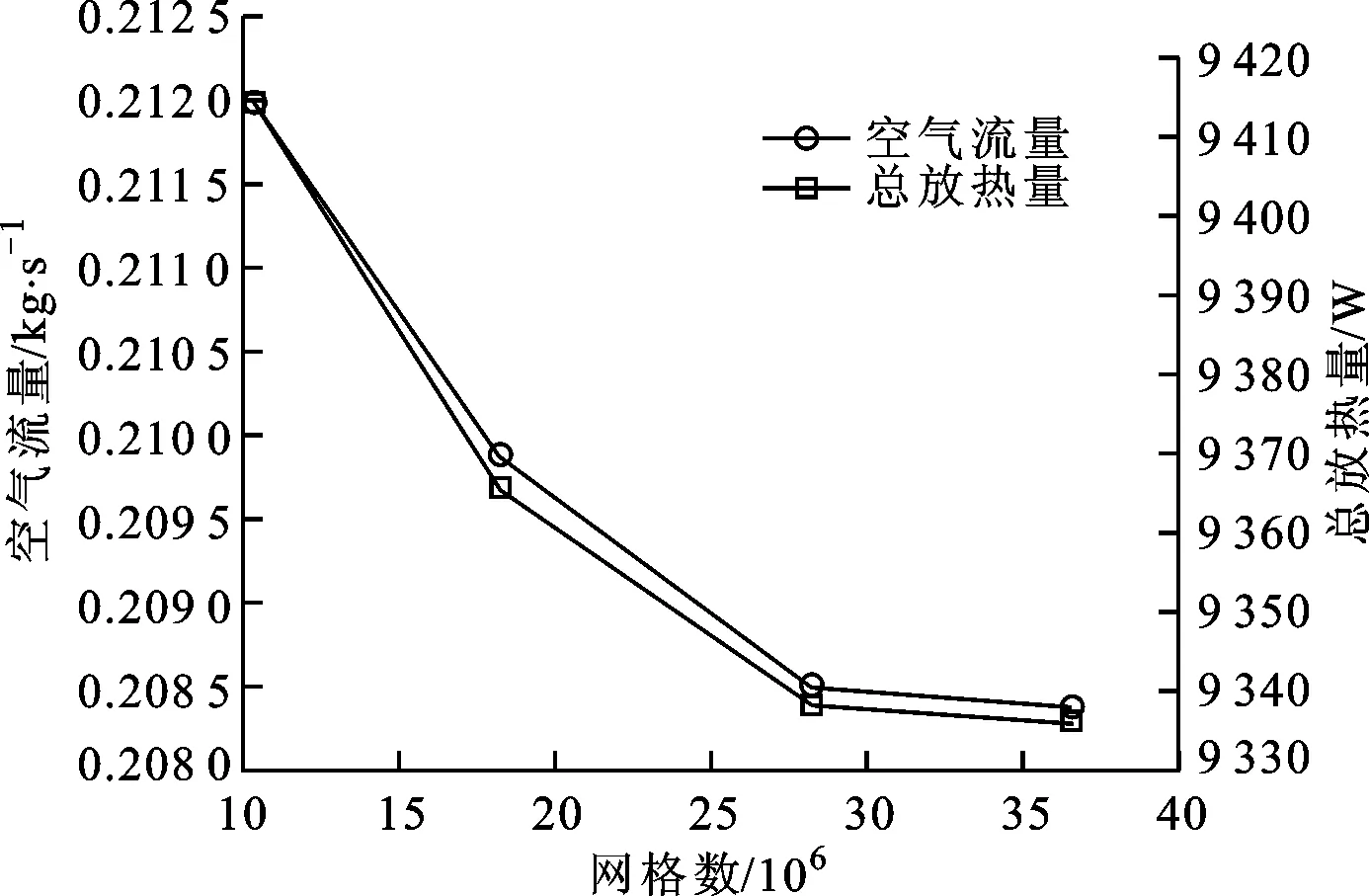
图4 网格无关性验证
2 实验验证
为了校核仿真的可靠性,对电机额定状态下稳态运行时的温度进行实验测量。
实验采用预埋热敏电阻的方法。实验系统主要由电源、测试电机、负载电机、计算机控制系统等组成[14],其中实验电源采用静态正弦电源。
由于转子高速旋转,难以实时测量其温度,且仿真结果表明转子相比定子温度较低,转子部分不会发生超温,因此实验主要测量定子线圈的温度。测点布置在周向0°、90°、180°、270°,即图5a中的1、2、3、4号槽口位置。测量以上4个线圈在轴向中心截面两侧的温度,如图5b所示。

(a)横截面
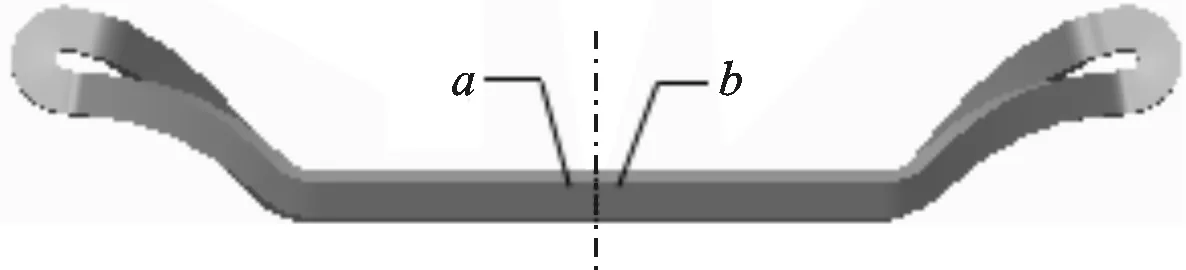
(b)纵截面图5 实验测点布置示意图
实验的相关参数如表4所示。实验过程中电机保持在额定工况下运行,额定转速为2 014 r/min,运行240 min后认为温度场达到稳态(即1 h内温度变化小于1 ℃),开始测温。实验结果如表5所示,将中心截面两侧的温度取平均,近似认为是中心平面的温度。
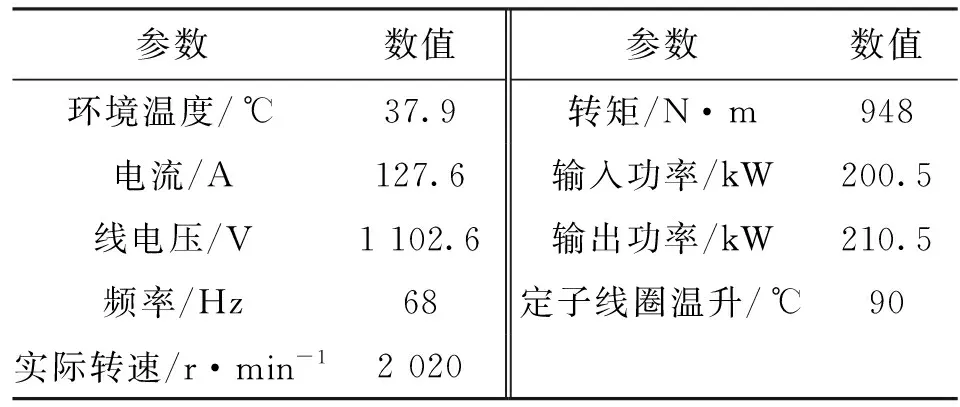
表4 相关实验参数

表5 实验测得的定子线圈温度
实验结果表明:周向180°和270°处的温度明显高于周向0°、90°,主要原因是1、2号槽口之间、1、4号槽口之间、2、3号槽口之间的机箱表面均存在支撑组件,如图5a所示,这些附件结构在很大程度上增大了散热面积,导致3、4号槽口处的温度最高。1号槽口定子线圈温度略高于2号,主要原因是1号槽口上面存在电气接线盒,电气接线盒内有空气存在,为热的不良导体,在一定程度上阻碍散热。
统计对应线圈在轴向中心截面的仿真计算温度,并将仿真计算结果与实验结果进行对照,计算相对误差如表6所示。

表6 数值模拟结果校核
校核表明仿真最大相对误差小于8.0%,满足工程要求,验证了本文数值模拟方法的可靠性。
对比仿真结果与实验结果发现,仿真计算温度略小于实验温度。误差来源分析如下:第一,实验中热敏电阻贴在绝缘层表面,实际测得温度为绝缘层的温度,仿真计算的是定子线圈的温度,两者之间有一定偏差;第二,仿真中将损耗近似为均匀分布,导致了一定误差。
3 仿真结果与分析
3.1 流场结果与分析
图6给出了求解域纵截面(z=0平面)的速度分布云图。由图可以看出:风扇叶顶速度最大,达42 m/s,因为所有旋转部件转速相同,而风扇叶顶半径最大,故转速最高,根据无滑移边界uair=uwall,叶顶处应有最大流速;定转子气隙中平均流速约为23 m/s,雷诺数Re=ud/ν=18 750,处于较强湍流状态;定子端部线圈附近空气也具有一定速度,可为定子端部线圈起到一定冷却作用。

图6 z=0平面速度云图
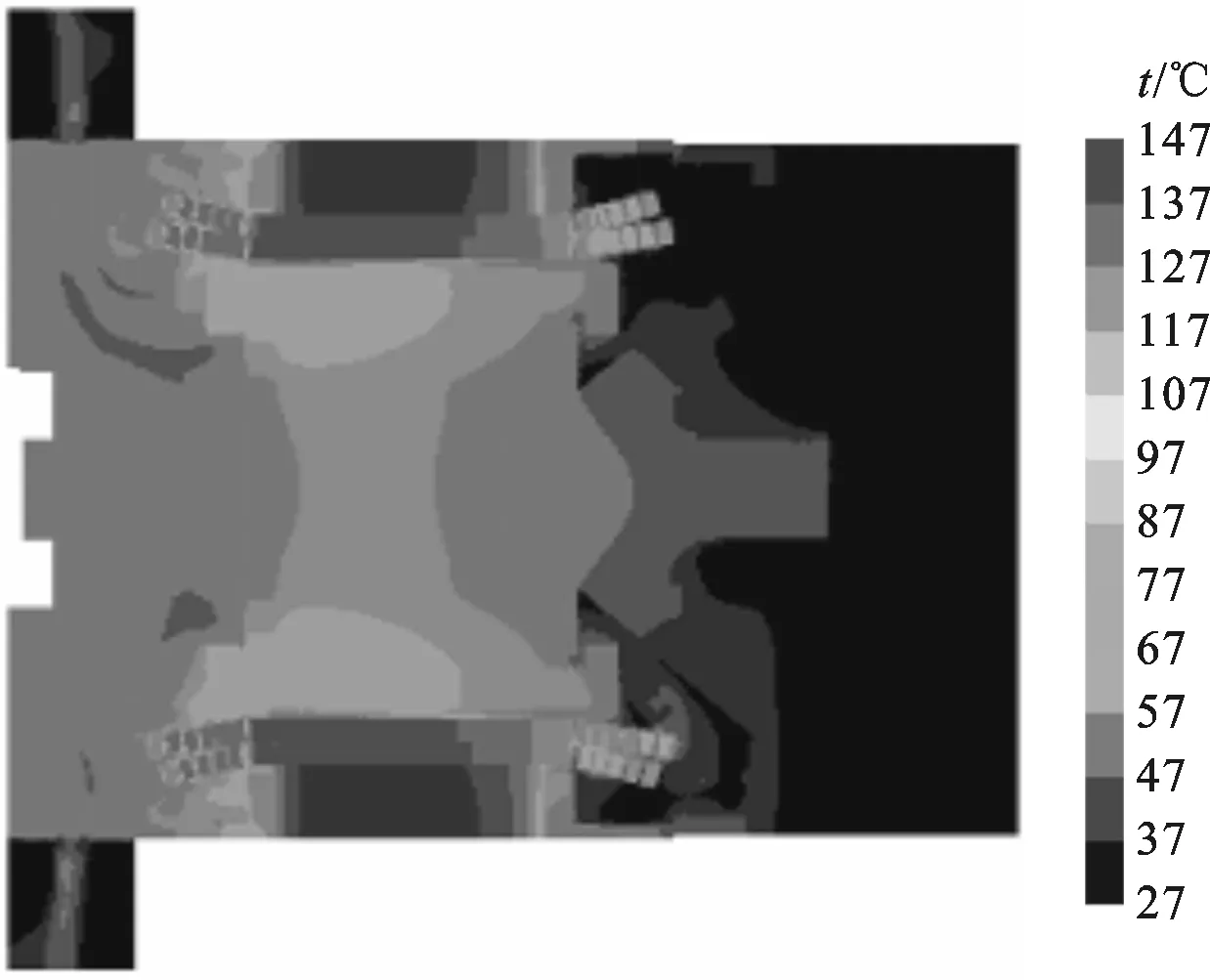
图7 z=0平面温度云图
3.2 温度场结果与分析
图7给出了z=0平面的温度云图。由图可以看出:定子部分温度最高,转子线圈和铁心温度较低,两者温差约为50 ℃。因为该带载工况下,定转子的体积损耗在同一数量级,主要影响温度分布的因素是热边界条件。定子铁心外侧为空气中自然对流的边界条件,近似为绝热,热量很难通过定子铁心外壁面散出。从转子径向看,不仅内侧有转轴轴向导热,且铁心内部有12个通风孔,外侧有定转子气隙的强制对流换热对其进行冷却。此外,从转子轴向看,转子两端都有高速流动的空气,也可提供较好的冷却环境。
图8给出了定子线圈在4号槽内的温度沿轴向的分布。
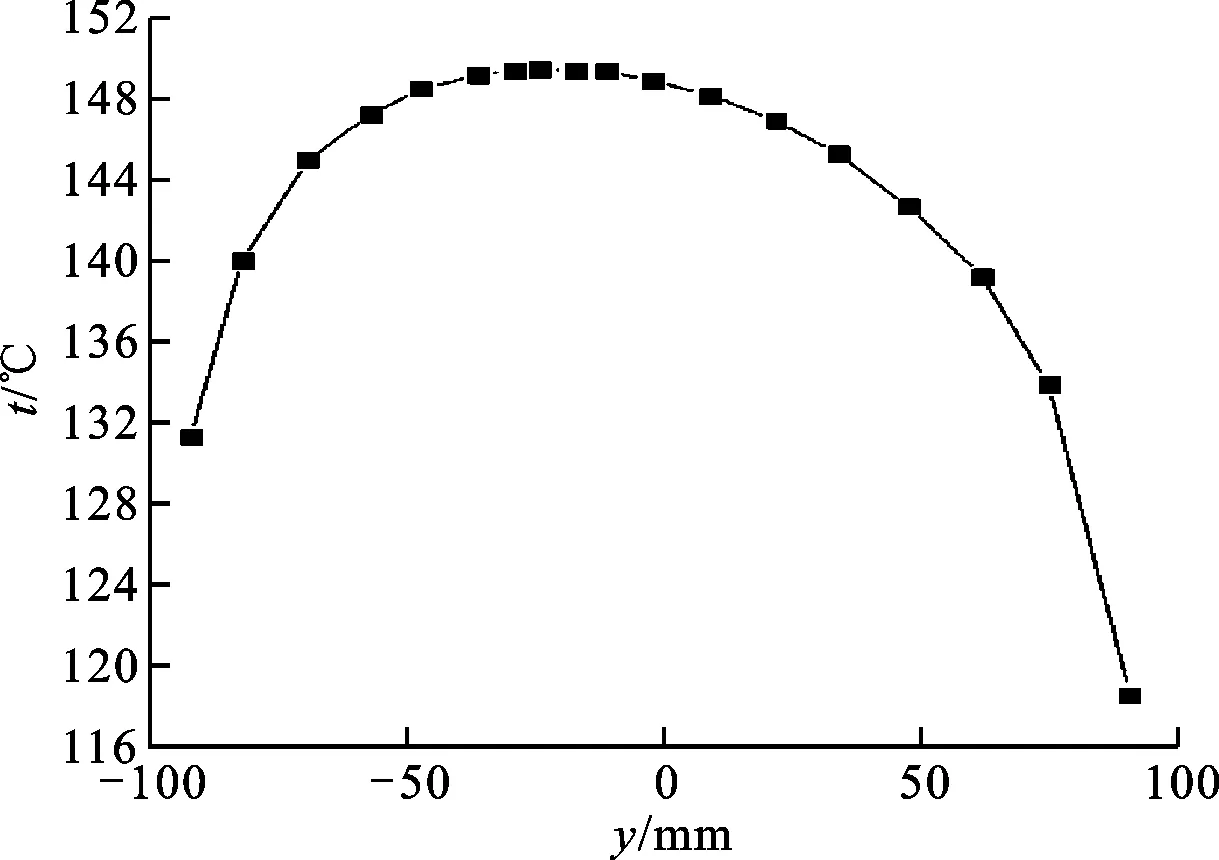
图8 4号槽定子导线沿轴向的温度分布
由图8可以看出,槽内定子线圈温度沿轴向不是严格对称分布,最高温度达149.4 ℃,位于轴向中心截面偏离非传动端一侧(即空气出口侧)约25 mm处。因为出口处的空气温度比入口的空气温度高,故空气出口的冷却效果比入口处的更差。此外,最高温度149.4 ℃小于该电机所用绝缘材料的绝缘等级H级对应允许最高温度180 ℃,故在额定状态下运行不会超温。
3.3 影响因素分析
本文对电机在额定带载状态下不同转速时的流动与传热进行了分析,相关研究表明铁耗近似随转速线性变化[15]。基于此结论,得出不同转速下的流量和定子线圈最高温度和最高温升如图9、图10所示。图9表明,随着电机转速增大,电机进出口空气流量近似线性升高。
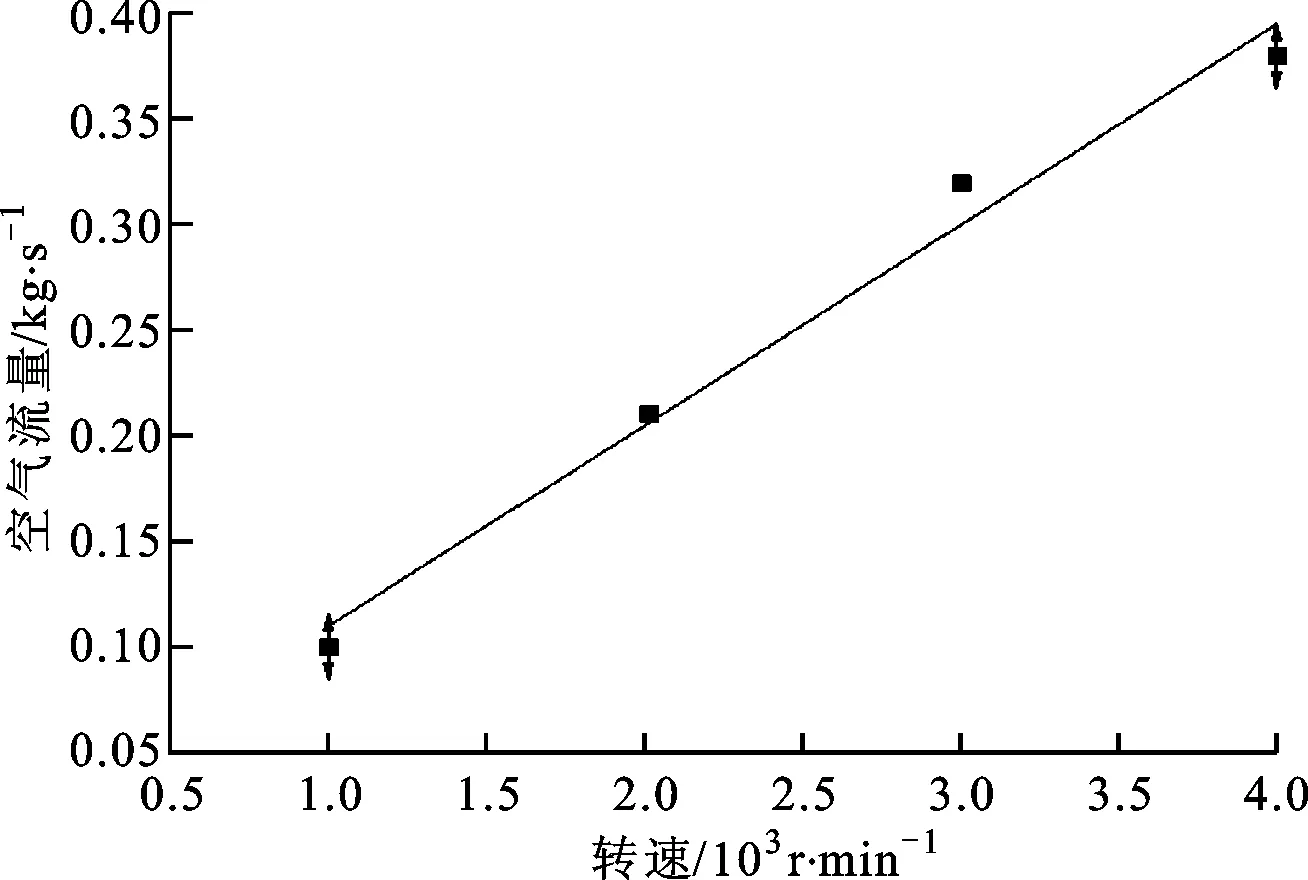
图9 转速对空气流量的影响
温升指电机中定子线圈高出环境的温度。图10给出了电机转速对定子线圈最高温度和最大温升的影响,可以看出,随着电机转速增大,定子线圈最高温度和最大温升都近似随之线性升高。转速每升高1 000 r/min,定子线圈最高温度升高6.2%,最大温升平均升高7.5%。尽管电机转速增大,空气流量增大,冷却能力增强,但是铁耗也随着转速增大,导致定子线圈温度随转速增大而上升。

图10 转速对定子线圈最高温度及最大温升的影响
此外,本文还研究了电机工作在10,20,30,40 ℃下的流动传热特性,结果如图11所示。
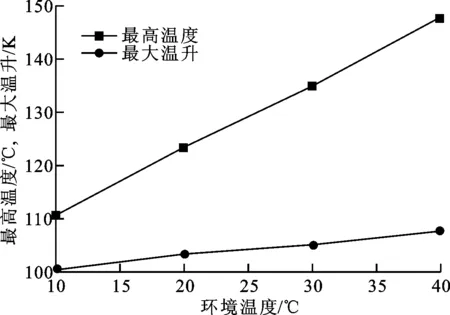
图11 环境温度对定子线圈最高温度及最大温升的影响
图11表明,随着环境温度升高,定子线圈最高温度近似随之线性升高,最大温升也随着环境温度升高略有升高,与最高温度变化趋势相比,增长幅度较小。环境温度每升高10 ℃,最高温度提高10.1%,最大温升提高2.3%。当环境温度达到40 ℃时,最高温度达149.4 ℃,是常见的最危险的工作环境。环境温度较高时,空气与电机之间温差变小,空气对电机的冷却效果显著变差,电机运行时更易超温。
对比环境温度与转速对最高温度与最大温升的影响,发现环境温度对最高温度影响更显著,对温升的影响略小。
4 结 论
本文对自通风电动机在额定工作状态下的流动传热特性进行了数值分析,对温度场进行了实验测量,并探究了环境温度与转速对流动传热特性的影响,得出以下结论:
(1)电机温度沿轴向和周向分布都呈现出不对称性。在周向,底部和接线柱之间温度最高。实验表明,周向不同槽口定子线圈温差可达10 ℃。在轴向,中心截面偏非传动端约25 mm处温度最高,非传动端温度高于传动端。因此,将电机简化为对称模型,取1/N部分计算会带来较大误差。
(2)随着电机转速增大,定子线圈最高温度近似随之线性升高,当电机达到最高转速4 000 r/min时,定子线圈温度最高,达160 ℃;随着电机工作环境温度升高,定子线圈最高温度近似线性升高,定子线圈最大温升也有小幅度升高,当环境温度达到40 ℃时,最高温度达149.4 ℃,最大温升达108 K,分别小于其表面包裹的H级绝缘等级最高允许温度180 ℃和最高允许温升125 K,因此电机设计中应以在最高环境温度和最高转速下运行作为设计热校核的标准工况。
(3)定子温度比转子温度平均高出50 ℃,转子基本不会引起电机超温,要消除电机的超温隐患,应从定子着手。

