滑动轴承椭圆度对转子加速过程振动响应的影响

张磊,徐华,2,裴世源

(1.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安;2.新疆大学机械工程学院,830047,乌鲁木齐)

旋转机械由于存在不平衡,在加速过程中振动幅值会发生变化,表现出复杂的动力学特性,当达到临界转速时其转子为柔性系统,振动幅值非常大,如果没有采取有效的抑振措施,会对转子系统的安全稳定运行产生极大的危害。传统的固定瓦轴承是基于某种特定工作状况进行设计的,当转速等工况条件改变时,固定瓦轴承无法根据实际工况调节轴承参数,可能造成转子振动过大、轴承损伤等安全性问题,严重影响转子-轴承系统的稳定运行。因此,为了提高系统的稳定性,减小转子的振动,很有必要提出一种合理有效的抑振方法。

变工况下转子-轴承系统的动力学特性一直是学者们研究的热点,为了使旋转机械安全稳定运行,国内外学者提出了很多抑制转子振动的方法。例如:Kirk等将动力减振器理论应用于弹性支承转子,研究了支承弹性和阻尼对单质量柔性转子同步响应的影响[1];Iwada等采用轴承支撑座的自优化理论,研究了基于自优化支撑系统的转子振动控制[2];Ishida等提出了不连续弹簧的概念,利用不连续弹簧特性抑制旋转机械振动[3];Nonami等采用最优调节器理论,利用主动式轴承研究了转子系统的弯曲振动控制[4];Reinig等利用旋转机械系统的扰动调节控制器来抑制旋转机械的振动[5];Nonami等通过变速度反馈法研究了柔性转子系统的动力学特性[6];Han等研究了在周期性摆角运动下柔性转子-轴承系统运行参数的稳定性[7];Rohit等基于椭圆轴承研究了其转子的动力学特征,指出在牛顿流体润滑条件下,椭圆轴承具有更好的使用性能[8];刘树鹏研究了舰船纵横倾作用下转子-轴承系统的动力学特性,得到了摇摆参数对系统动力学特性的影响[9];张宏献等研究了椭圆度对转子-轴承系统稳定性的影响[10]。

目前,学术界主要通过优化的弹性支撑系统和主动振动控制算法来抑制转子的振动,这些抑振方法一般是基于液压系统或者电磁系统,并且已经取得了一定的成效。本文提出一种基于机械传动原理的椭圆度可调转子-轴承系统,将主动控制应用于流体轴承,可以在不同转速下根据转子的实际振动情况调节轴承椭圆度,通过改变油膜厚度来抑制转子的振动,使转子加速过程中的振动幅值始终在安全范围内。

1 椭圆度可调滑动轴承-转子系统

旋转机械在经过临界转速时会产生很大的振动,若振动过大将会对机械结构造成破坏,因此减小临界转速的振动对旋转机械的安全运行十分重要。

图1所示是本课题组提出的一种椭圆度可调滑动轴承-转子系统装置。该装置的轴瓦分为上下两部分,上轴瓦固定在轴承座上,下轴瓦通过丝杠滑块机构实现上下滑动。当根据位移传感器采集的信号发现转子的振幅过大时,调节丝杠,通过转动丝杠2带动斜铁8移动,斜铁8的移动带动轴承下瓦6上下滑动,从而改变轴承的油膜间隙;轴承下瓦的垂直运动使油膜的刚度和阻尼特性发生变化,从而改变转子系统的动力学特性,减小转子的振动。

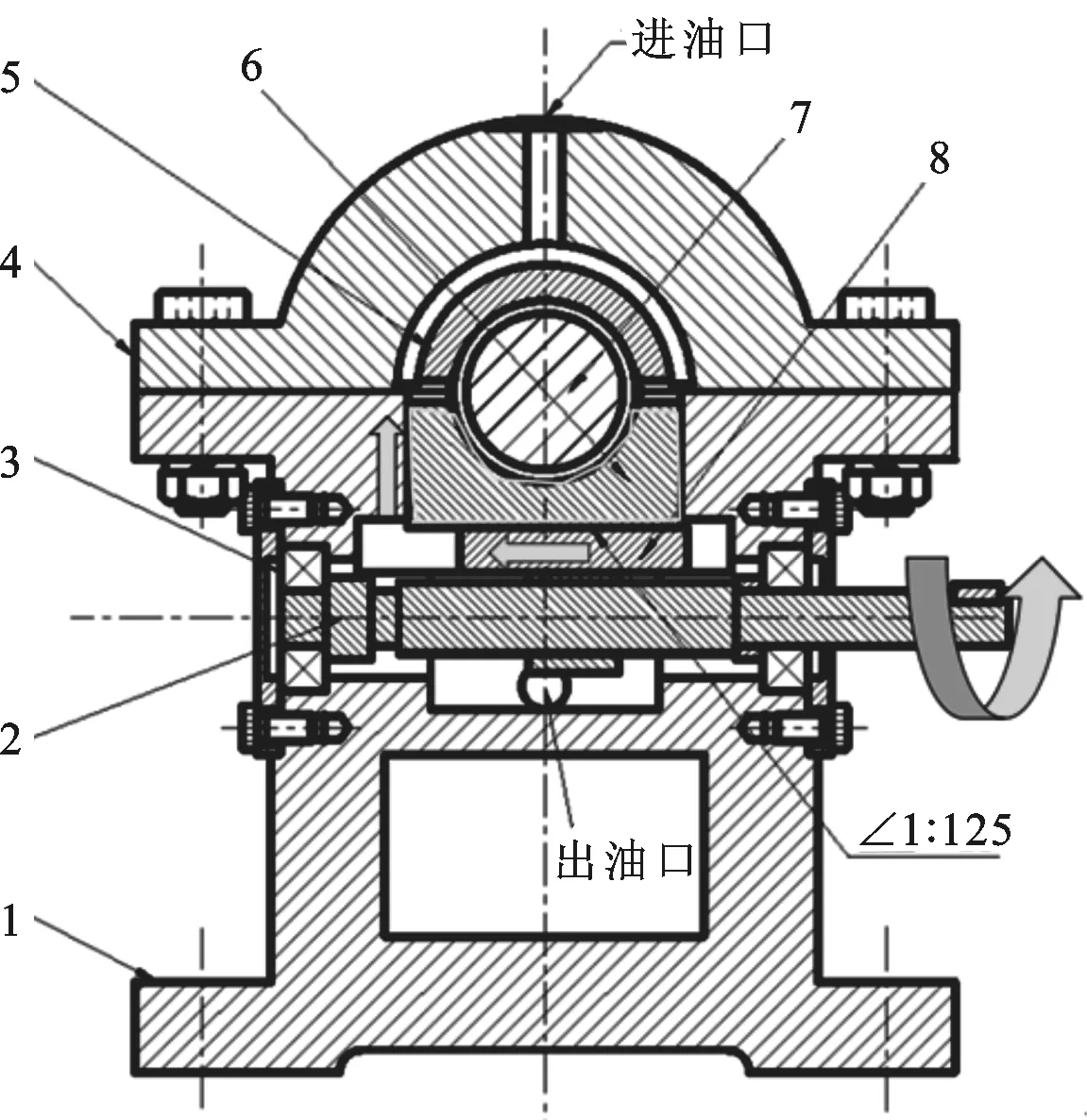
1:支撑座;2:梯形丝杠;3:丝杠轴承;4:支撑座上盖;5:轴承上瓦;6:轴承下瓦;7:转子;8:斜铁图1 椭圆度可调滑动轴承-转子系统装置图

椭圆度可调滑动轴承的结构如图2所示,轴承上瓦固定,下瓦可以沿着导轨上下滑动。当轴颈的振动情况发生变化时,通过可移动斜铁的水平滑动,带动轴承下瓦垂直滑动,从而改变油膜间隙,影响转子系统的标高,同时使轴承的刚度系数和阻尼系数发生变化,最终导致轴承支撑转子系统的动力学特性发生变化。

图2 椭圆度可调滑动轴承结构示意图

为了使椭圆滑动轴承具有明显的抑振作用,设计椭圆轴承的油膜间隙有较大的调节范围。轴承下轴瓦可上下移动的距离Cmin=48～144 μm,侧隙Cmax=160 μm,根据椭圆度计算公式

得到轴承椭圆度的调节范围为0.1～0.7(详细设计过程将另行撰文)。下面将以椭圆度为调节参数,通过调节轴承下瓦的移动距离,分别在不同的椭圆度下进行动力学分析,最终得到椭圆度可调滑动轴承-转子系统的动力学特性。

为了找出合理的调节方案来减小转子在加速过程中的振幅,需要研究不同椭圆度下轴承的动力学特性。使用西安交通大学润滑理论与轴承研究所研发的转子-轴承系统动力学分析软件DLAP(dynamic lubrication analysis program),计算不同椭圆度下油膜的刚度和阻尼系数。该软件通过小扰动法求解非定常工况的雷诺方程得到轴承的动力学特性,并且已经经过多次验证[11-12],计算结果可靠。图3显示了椭圆度对刚度系数的影响,图4则显示了椭圆度对阻尼系数的影响。图中:Kxx代表水平方向的刚度系数,Kyy代表垂直方向的刚度系数;Dxx代表水平方向的阻尼系数,Dyy代表垂直方向的阻尼系数。因为计算出来的交叉刚度和阻尼系数的数值很小,比垂直刚度和阻尼系数的值小2个数量级,对动力学计算几乎不产生影响,所以忽略不计。

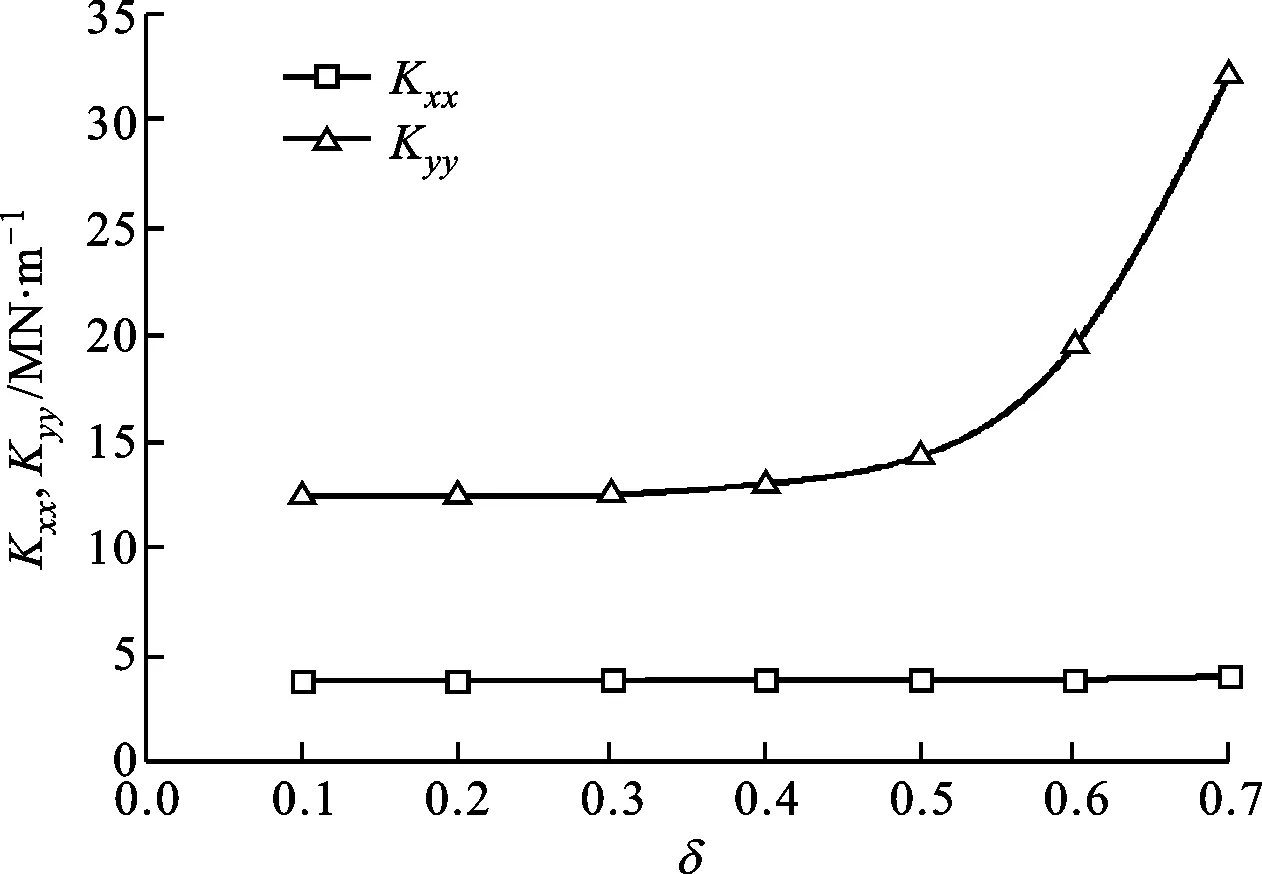
图3 椭圆度对油膜刚度系数的影响

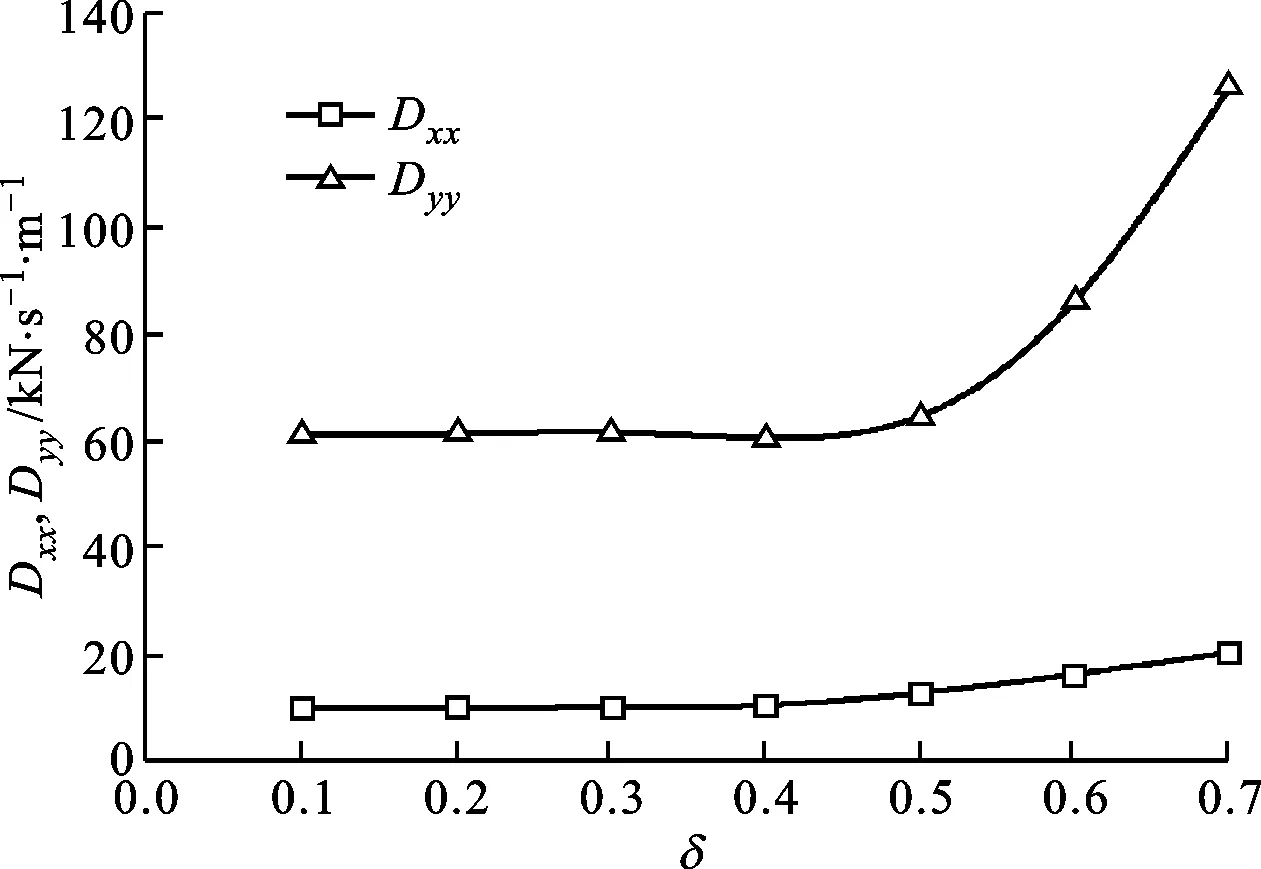
图4 椭圆度对油膜阻尼系数的影响

由图3、图4发现,随着椭圆度的增大,垂直方向的刚度和阻尼系数变化明显,而水平方向的刚度和阻尼系数变化比较小。这是因为椭圆度增大时,轴承下瓦向上移动,顶隙减小而侧隙不变,必然造成垂直方向的刚度和阻尼系数有很大变化,而水平方向的刚度和阻尼系数基本不变。当椭圆度增大到0.7时,垂直方向的刚度系数增大到初始值的2.5倍,水平方向的刚度系数增大了0.3倍;垂直方向的阻尼系数增大到初始值的2倍,水平方向的阻尼系数增大了0.7倍。通过计算得到不同椭圆度下轴承刚度系数和阻尼系数的变化规律,可以为随后的动力学研究提供参考。

2 椭圆度可调滑动轴承-转子系统的动力学分析

2.1 转子加速过程的动力学模型

转子加速过程中系统的动力学特性会发生很大变化,当接近临界转速时,转子的振幅会急剧增大,而过大的振动会威胁到转子系统的安全运行。下面将利用本文提出的椭圆度可调滑动轴承,研究在振幅过大时,通过调节椭圆度改变油膜间隙来抑制转子振动的方法,以提高转子运行的稳定性。

图5 圆轴承支撑时转子系统加速过程的振动响应

图5所示是圆轴承支撑时转子系统加速过程的振动响应,可以看出随着转速n的增加转子垂直方向的振幅Ay增大,当转速达到临界转速附近时振幅急剧增大,这时转子系统存在安全隐患。为了减小振幅,使转子系统安全稳定地运行,可以在达到临界转速前通过调节油膜间隙来减小振幅。图5中的虚线表示振动的安全阈值,当振幅超过虚线后转子系统可能无法正常运行;2条竖实线中间的区域就是需要调整椭圆度以减小振幅的转速区域。

为了研究椭圆度可调滑动轴承-转子系统加速过程的动力学特性,建立对应的转子-轴承系统模型,如图6所示。在转子的两端安装轴承,中间安装质量盘,然后通过调节椭圆度来改变轴承的油膜间隙,研究不同椭圆度下转子-轴承系统的动力学特性。转子-轴承系统的参数如下:最大转速3 000 r/min;转子长度1 350 mm;转子直径40 mm;质量盘直径230 mm;质量盘厚度90 mm;杨氏模量206 GPa;密度7 850 kg/m3。

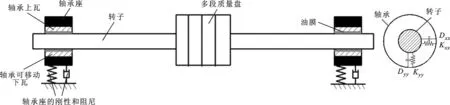
图6 椭圆度可调滑动轴承-转子系统模型

根据转子系统的结构参数建立两端轴承支撑的转子系统有限元模型,整个有限元模型离散为9个节点,共8个单元、18个自由度,如图7所示,其中M、K、C分别为转子系统的质量矩阵、刚度矩阵和阻尼矩阵,Q为系统的自由度,F为系统所受的载荷。轴承矩阵分布在第2和第8个节点位置,质量盘矩阵在第5个节点位置。当系统的椭圆度改变时,只需要把相应椭圆度下的刚度和阻尼代入轴承节点的矩阵中,然后建立对应的动力学方程来求解响应。

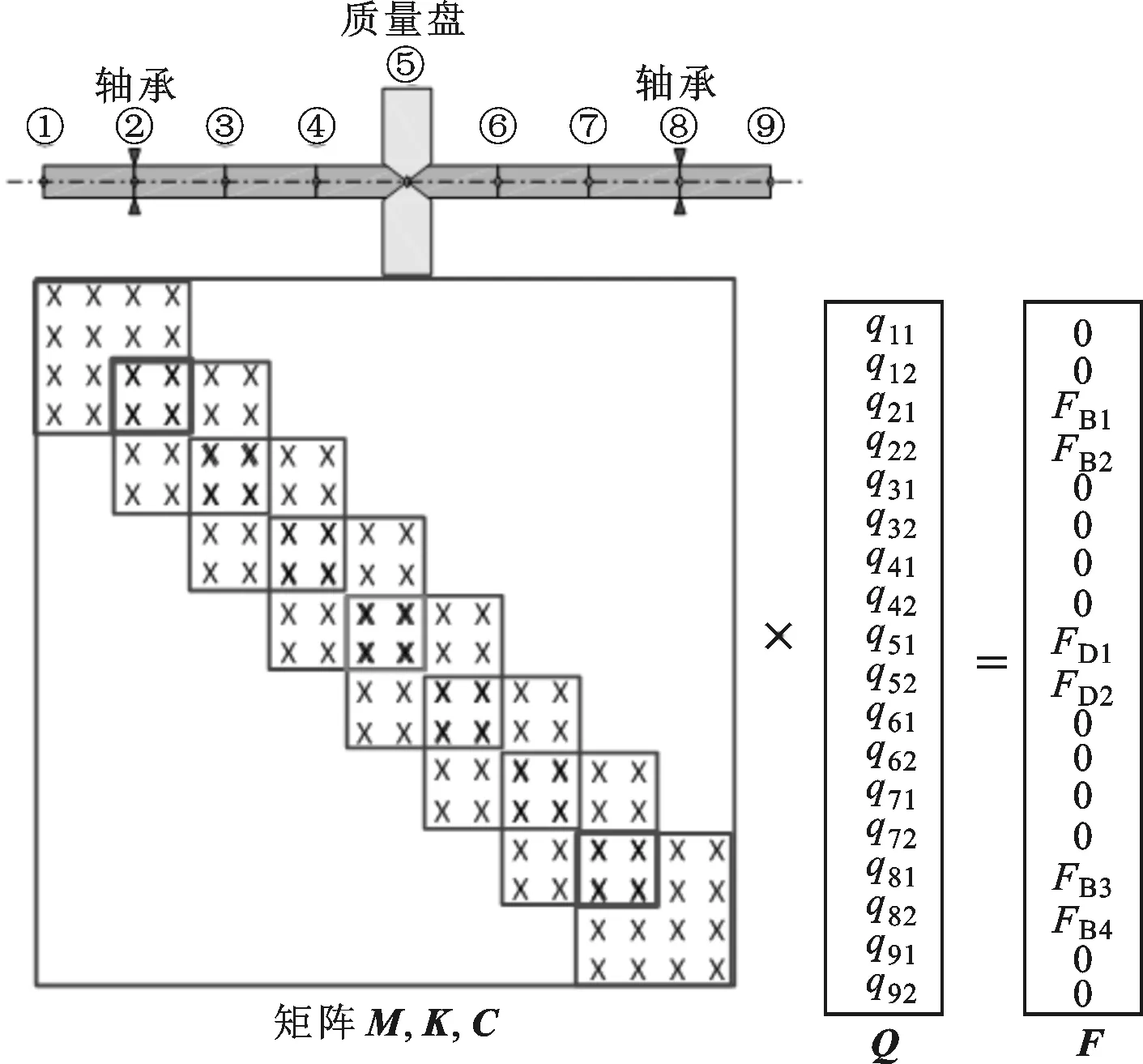
图7 动力学矩阵的组装

转子-轴承系统的动力学方程为

Mq″+Cq′+Kq=F

位移响应计算公式为

q=[-Ω2M+jΩ(ΩG+C)+K]-1·

式中:M为结构质量矩阵;C为阻尼矩阵;K为结构刚度矩阵;q为位移向量;F为载荷矩阵;G为陀螺矩阵;m为转子的总质量;ε为偏心距;Ω为转子的角速度;δ为相位角;Id为转子的惯性矩;Ip为转子的极惯性矩;γ=Ip/Id。阻尼矩阵C考虑了陀螺效应和Rayleigh阻尼矩阵,其中Rayleigh阻尼矩阵为M和K的线性组合,即αM+βK,其中α和β是不依赖于频率的常数,它们与系统的阻尼系数和前2阶固有频率有关。F由不平衡力和重力组成。

2.2 不同椭圆度下转子系统的动力学响应

利用图6所示椭圆度可调轴承-转子模型,研究了不同椭圆度下转子系统的动力学响应。根据图3、图4可得到不同椭圆度下轴承的刚度和阻尼值,再把刚度和阻尼值分别代入动力学方程中,然后利用Runge-Kutta变步长积分求解动力学方程,得到转子加速过程的动力学响应。

设转子以1.5 rad/s2的恒定加速度经过临界转速,分别设置轴承椭圆度为0.1、0.3、0.5和0.7,计算转子系统加速过程的振动响应。图8、图9分别是不同椭圆度下转子在中间位置和轴承位置的振动响应图,其中Am,x、Am,y分别代表质量盘处转子水平方向和垂直方向的振幅,Ab,x、Ab,y分别代表轴承位置转子水平方向和垂直方向的振幅。

(a)水平方向的响应

(b)垂直方向的响应图8 转子在质量盘处的振动响应计算结果

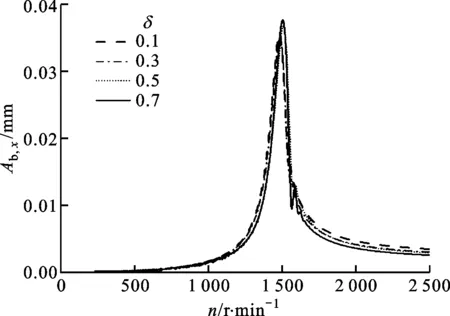
(a)水平方向的响应

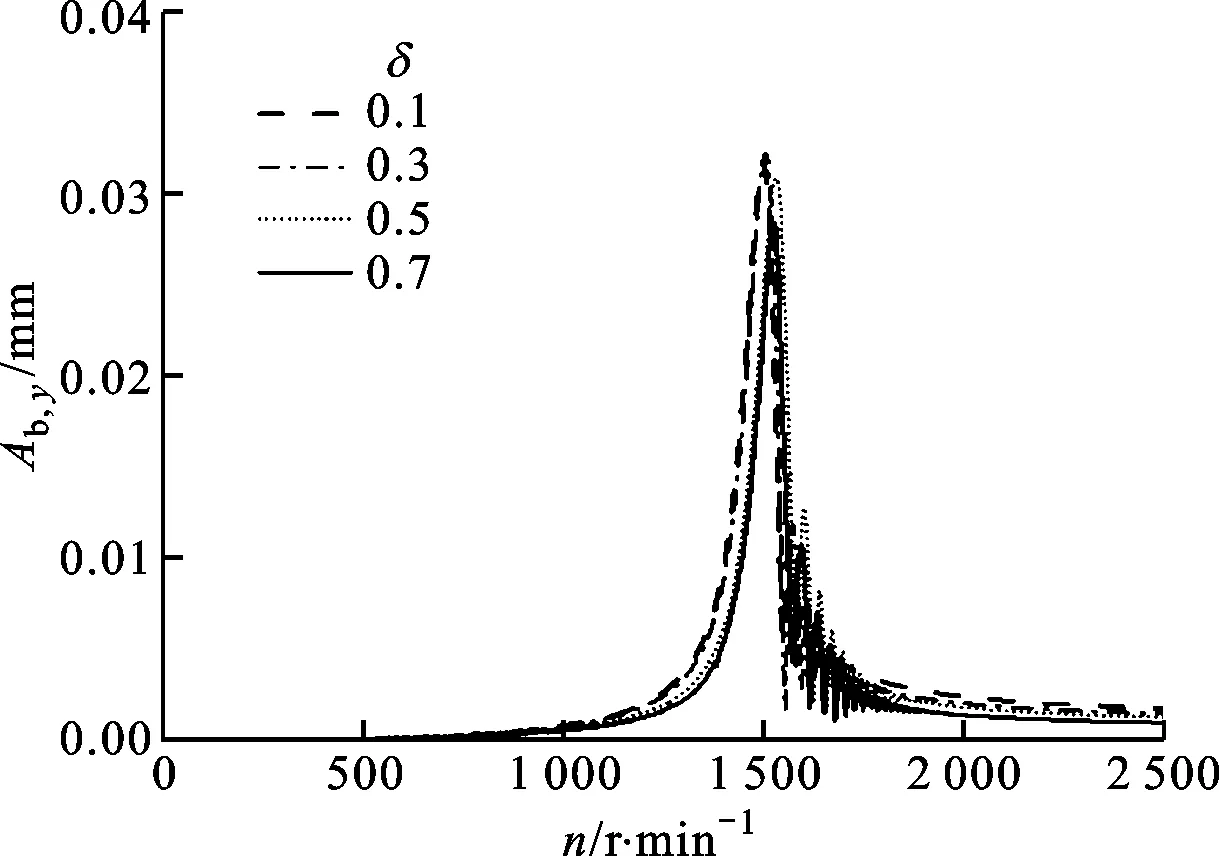
(b)垂直方向的响应图9 转子在轴承支撑处的振动响应计算结果

从图8可以看出:转子振幅的减小程度与轴承椭圆度有紧密联系,经过临界转速时椭圆度越小抑振效果越明显;通过引入椭圆度可调滑动轴承,转子经过临界转速时转子盘处的振幅最多可降低36%。

由图3、图4可知,椭圆度越小则对应的刚度系数和阻尼系数也越小,因此可以得出结论:在临界转速时,较小的刚度和阻尼系数可以导致更强的振动抑制效果。当椭圆度从0.7调到0.1后,垂直方向的振幅从2.25 mm减小到1.45 mm,水平方向的振幅从1.35 mm减小到0.85 mm,水平方向和垂直方向有几乎相同的抑振效果。

由图9可知,在椭圆度的调节过程中,转子在轴承位置的响应幅值没有出现剧烈的变化,说明在临界转速时,调节椭圆度对轴承位置的振动不会产生很大影响,但是在2 000～2 500 r/min范围内,转子的振幅有增大的趋势,大约增大了20 μm,这是因为这个转速范围远离临界转速,转子表现为刚性转子,这时椭圆度减小会增大转子的振动。由此可以得出结论:在远离临界转速时,可以通过增大滑动轴承的椭圆度来抑制转子的振动。

上面的计算结果表明:当转子通过临界转速时,转子表现为柔性转子系统,这时较小的椭圆度对应较小的刚度系数和阻尼系数,可产生较强的振动抑制作用;当转子远离临界转速时,转子表现为刚性转子系统,这时较大的椭圆度对应较大的刚度系数和阻尼系数,也可产生较好的振动抑制效果。

3 椭圆度可调滑动轴承-转子系统的试验研究

3.1 设计并搭建转子轴承系统试验台

为了验证前面的理论计算,自主设计并搭建了与数值分析模型完全一致的转子-轴承系统试验台,图10是试验台设计方案及数据采集方案。2对位移传感器成90°分别安装在轴承支撑处和转子中间位置,采集转子在这2个位置的水平和垂直方向振动,这样的数据采集方案可以测量轴承位置的运转状况和转子的最大振幅,实时监测整个转子-轴承系统的工作状态。

3.2 轴承结构及椭圆度调节方法

图10 试验台设计方案及数据采集方案

3.3 试验方案

本次试验的目的是研究轴承椭圆度和转速等因素对转子振动的影响。根据试验目的,结合试验台的实际情况,设计试验步骤如下。

首先把椭圆度调节为0.1,在30 s内转速从0直线加速到2 700 r/min,测量轴承和质量盘位置处转子的振动位移;然后将椭圆度分别调至0.2、0.3、0.4、0.5、0.6、0.7,重复采集轴颈的振动位移;最后在20 s内从2 700 r/min直线减速停机。采样频率为3 124 Hz,每隔1 s采集一次,每次采集时间为1 s,每个工况采集60 s。

3.4 试验结果分析

按照试验步骤采集试验数据,并绘制加速过程中转子的振动位移曲线,如图11、图12所示。

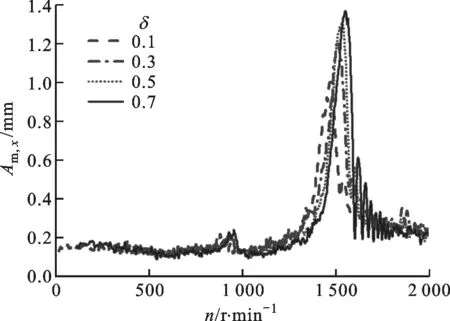
(a)水平方向的响应

(b)垂直方向的响应图11 不同椭圆度下转子在质量盘处的振动响应

由图11可知,较小的椭圆度具有较强的抑振作用。随着椭圆度从0.7调整到0.1,转子通过临界转速时质量盘处的振幅显著减小,在水平方向上从1.4 mm减小到0.96 mm,在垂直方向上从2.2 mm减小到1.5 mm,减幅高达31.8%,说明转子在经过临界转速时,通过调节椭圆度可以有效抑制振动,并且水平方向和垂直方向的抑振效果相同。由图12可知,通过调节椭圆度,轴承支撑处转子的振幅不会出现剧烈变化,随椭圆度从0.7调整到0.1,转子经过临界转速时的振幅略有增大。

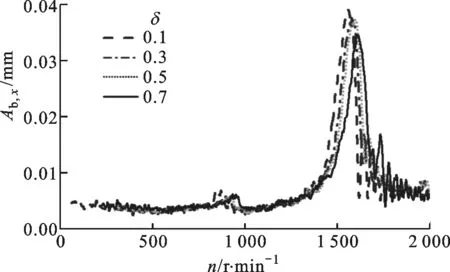
(a)水平方向的响应

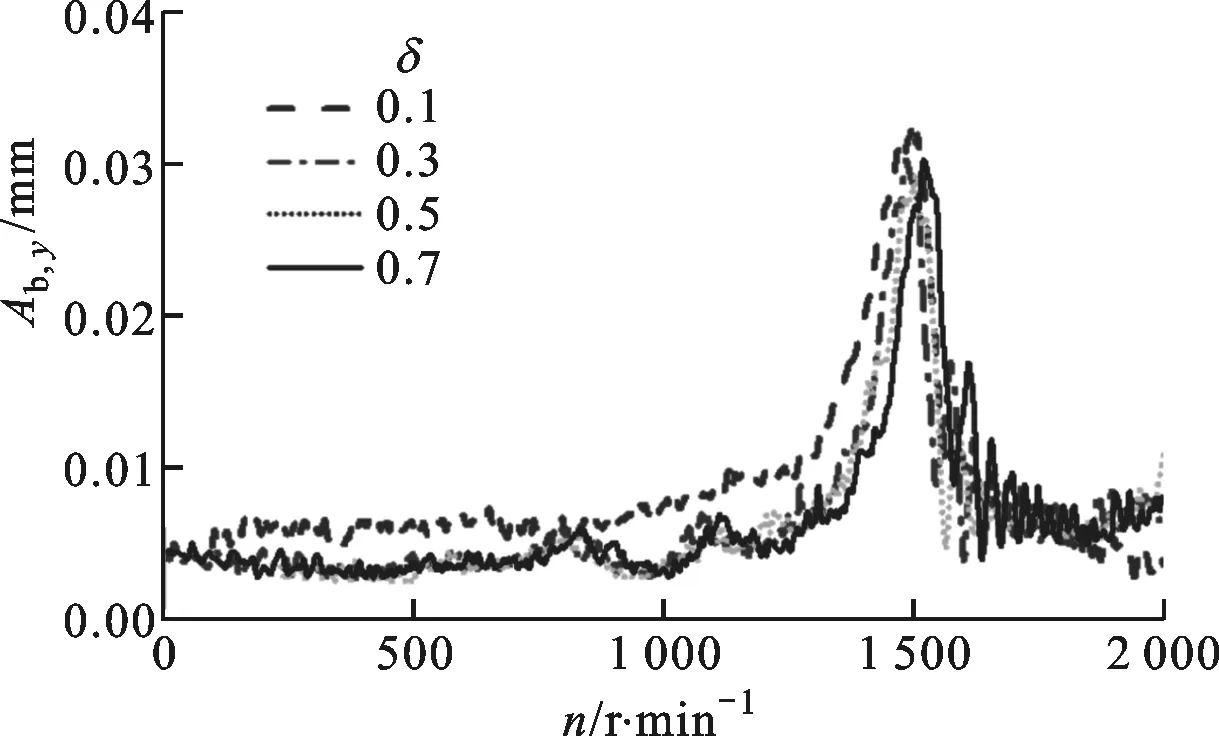
(b)垂直方向的响应图12 不同椭圆度下转子在轴承支撑处的振动响应

试验得到的结果与前面理论计算的结果非常吻合,即当转子通过临界转速时,转子表现为柔性转子系统,这时较小的椭圆度可导致较强的抑制振动效果,抑振效果可以达到30%以上,并且水平方向和垂直方向的抑振效果几乎相同。

理论计算结果显示,在2 000～3 000 r/min转速范围内,减小椭圆度会在轴承位置出现振幅增大的趋势,与临界转速区域的结果截然相反,说明在远离临界转速的区域,增大椭圆度可能出现振幅减小的情况。因此,分别在1 000和2 000 r/min固定转速下调节椭圆度,研究转子的振动变化。

在1 000 r/min转速下采集不同椭圆度时的试验信号,并绘制出对应的时域频域信号图,如图13、图14所示,其中Ax、Ay分别为转子水平方向和垂直方向的振动幅值,A为转子系统的振动幅值,f为转子的振动频率。从这2个图中可以观察到,时域信号的变化比较有规律,频域信号除了转频外,其他信号的值很小,采集的信号中没有干扰信号。

图15是用转速为2 000 r/min、不同椭圆度下采集的试验数据绘制的轴心轨迹。由于篇幅限制,文中只绘制了椭圆度从0.1调节到0.7过程的轴心轨迹,但依然可以有效表明椭圆度调节过程中转子系统振动响应的变化情况。

(a)δ=0.1

(b)δ=0.3

(c)δ=0.5

(d)δ=0.7图13 不同椭圆度下采集数据的时域信号(转速为1 000 r/min)

(a)δ=0.1 (b)δ=0.3

(c)δ=0.5 (d)δ=0.7图14 不同椭圆度下采集数据的频域信号(转速为1 000 r/min)

(a)δ=0.1 (b)δ=0.3

(c)δ=0.5 (d)δ=0.7图15 不同椭圆度下的转子轴心轨迹(转速为2 000 r/min)

从图15可以看出:转子的轴心轨迹呈椭圆形;在固定转速下,转子振动的幅值随轴承椭圆度的增大而减小;随椭圆度从0.1调节到0.7,轴心轨迹逐渐减小,减小程度达到50%以上。

由图15还可以发现,当椭圆度为0.3时,轴心轨迹出现了大圈套小圈的现象。由图16所示的频谱分析结果可以看出,当椭圆度调到0.3时,系统除了因为质量不平衡导致的转子同频振动外,还出现了一个新的振动分量,频率为转频的一半。这个振动分量是由滑动轴承的油膜涡动造成的,图15中出现的轴心轨迹大圈套小圈即是由于发生了油膜涡动。油膜涡动一般不会破坏轴承的正常润滑,对转子的正常运行影响不大,但是它是转子-轴承系统开始出现失稳的前兆。

(a)δ=0.1 (b)δ=0.3

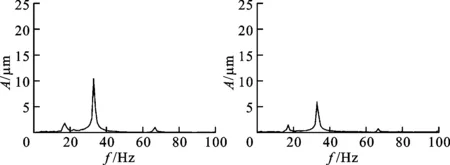
(c)δ=0.5 (d)δ=0.7图16 不同椭圆度下的转子振动频谱分析结果(转速为2 000 r/min)

由图16还可以发现,出现油膜涡动后再继续增大椭圆度,则同频振动分量和半频分量都减小,这说明即使出现了油膜涡动,通过调节椭圆度仍然可以有效抑制转子的振动。

4 结 论

(1)滑动轴承的椭圆度对刚度系数和阻尼系数影响很大。转子-轴承系统在升速过程中,通过调节椭圆度改变油膜间隙,可以有效地改变转子-轴承系统的动力学特性;合理地调节椭圆度,能够提高转子系统的稳定性。

(2)减小滑动轴承的椭圆度可以抑制临界转速区域的振动。在经过临界转速区域时,转子属性表现为柔性转子系统,这时通过减小椭圆度来增大油膜间隙,能有效地抑制转子的振动,抑振效果可以达到30%以上,并且水平和垂直方向的抑振作用几乎相同。

(3)增大滑动轴承的椭圆度可以抑制临界转速以外区域的振动。在远离临界转速的区域,转子属性表现为刚性转子系统,这时通过增大椭圆度来减小油膜间隙,同样能有效地抑制转子的振动,抑振效果可以达到50%以上,并且即使出现油膜涡动,增大椭圆度仍然可以有效减小转子的振动。