重载下滚动直线导轨副的接触特性

田红亮,余媛,杜义贤

(三峡大学机械与动力学院,443002,湖北宜昌)

滚动直线导轨副具有运动灵敏度高、定位精度高、牵引力小、磨损小和润滑维修简便等优点,已逐渐取代了传统的滑动直线导轨副(重载机床除外),成为目前数控机床的重要功能部件。滚动直线导轨副通常连接工作台和主轴箱,其动力学特性直接影响机床的加工精度和加工效率,因此,对滚动直线导轨副的动力学特性进行测试、建模和分析是机床整机动力学分析的基础,对于数控机床的抗振性和稳定性设计具有重要的作用。因为滑块沿直线导轨运动的方向是工作方向,所以在进行受力分析时不在此方向上施加力,视为在此方向上是固定约束[1]。

多年以来,科研人员在实验和理论上对滚动直线导轨副的接触特性进行了许多研究。例如:毛宽民等基于赫兹接触理论分析了滚珠和滚道之间接触量与接触力的关系,将滑块简化为一个刚体,建立了滑块的动力学方程[2],还将滚动直线导轨副的可动结合部视为一个独立无质量的八结点六面体单元,每个结点之间相互耦合,利用刚度影响系数法建立了动力学模型[3];王禹林等通过将变形量和偏心载荷等效分解,实现了导轨副5种静刚度的同时测量[4];马雅丽等分析了滚动直线导轨副固有频率与滚珠切向接触刚度影响因素之间的关系,建立了综合考虑切向与法向接触刚度的滚珠接触力学模型[5];田红亮等借助赫兹点接触形成椭圆接触区域的计算机制,考虑外加法向工作总载荷和法向预紧力,构建了滚动直线导轨副的运动结合部法向接触力学模型[6];刘耀等建立了滚珠直线导轨副的圆柱面-球面结合面数学模型,用解析方法求解外载荷作用时结合面的变形,研究了不同外载荷作用下滚珠直线导轨副圆柱面-球面结合面的静特性[7];孙伟等基于赫兹接触原理,对滚动直线导轨副进行了赫兹接触建模及接触刚度求解[8];王民等建立了滚珠直线导轨副接触刚度模型,基于赫兹接触理论对滚珠和滚道的接触面进行了力学与变形分析[9]。在上述研究中,分析滚动直线导轨副接触力学行为的方法有4个方面的不足:①文献[1]认为法向接触变形随法向外载荷的变化较好地符合幂函数规律,但文献[7]认为法向接触变形与法向外载荷成指数关系;②没有区分单个滚珠受到的预紧力与预载荷等级所对应的总预紧力;③只计算了滚动体与单个刚体的接触变形量,而更合理的是将滑块和直线导轨视为刚体,将滚珠视为弹性体,滑块和直线导轨沟槽的半径相等,这样滚珠与滑块沟槽之间的变形量等于滚珠与直线导轨沟槽之间的变形量[10];④只考虑了导轨副轻载时的情况,没有分析导轨副重载时的情况。

本文考虑滚珠与滑块、直线导轨的沟槽同时接触,计算了滚珠的接触变形量,对导轨副轻载时的各种静力学特性参数进行了改进计算,进而计算了导轨副重载时的各种静力学特性参数,最后给出了导轨副轻载和重载时多种参数的完整表达式。

1 滚动直线导轨副的接触

1.1 外力小于临界力时的改进算法

滚动直线导轨副由直线导轨、滑块和滚动体(滚珠或滚柱)组成,用作直线运动导向和支承的部件。假设滚动直线导轨副总共有4排通道沟槽,每排通道沟槽的滚珠数皆为N。滚动直线导轨副的滑块在垂直方向横截面上的整体受力接触情况如图1所示,其中O1和O2分别为滑块和直线导轨的静平衡位置,z1和z2分别为滑块和直线导轨向下的压缩量,F为整个滚动直线导轨副所受到的外力,Fu为直线导轨上排任意一个滚珠对滑块的斜上支反力,Fl为直线导轨下排任意一个滚珠对滑块的斜下支反力。

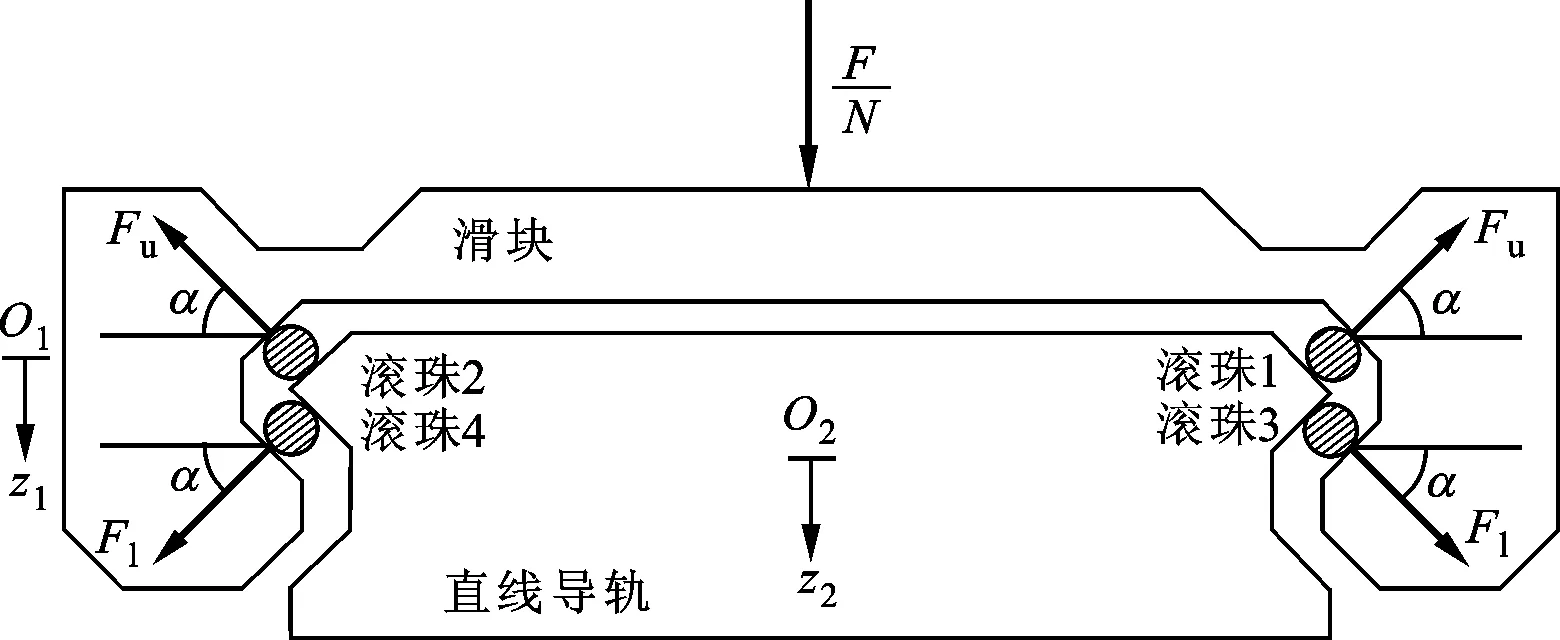
图1 滑块在垂直方向横截面上的受力情形

如果4排滚珠在外力作用下始终处于压缩状态,滑块在垂直方向上的静力平衡方程为

(1)

强调作用力和反作用力必须在同一直线上是牛顿第三定律的强形式。作用力与反作用力相等而方向相反,是以力的传递不需要时间即传递速度为无限大为前提的。滑块对直线导轨上排任意一个滚珠的斜下压缩力

(2)

式中:H为赫兹类接触刚度;δu为直线导轨上排任意一个滚珠在滑块作用下的斜下压缩量,也是该滚珠在直线导轨作用下的斜上压缩量,故该滚珠的总压缩量为2δu。

滑块对直线导轨下排任意一个滚珠的斜上压缩力

(3)

式中:δl为直线导轨下排任意一个滚珠在滑块作用下的斜上压缩量,也是该滚珠在直线导轨作用下的斜下压缩量,则该滚珠的总压缩量为2δl。

单个滚珠受到滑块或直线导轨的预紧力

(4)

式中:δ0为单个滚珠在滑块或直线导轨作用下的初始压缩量,即该滚珠的总初始压缩量为2δ0。

滚珠1和4在受预紧力前、后和在受外力时的变形协调情况如图2所示。当滚珠1承受外力后,因所受的压缩力增大而继续被压缩,其压缩变形量增大δ。当滚珠4承受外力后,因所受的压缩力减小而被放松,其压缩变形量减小δ。

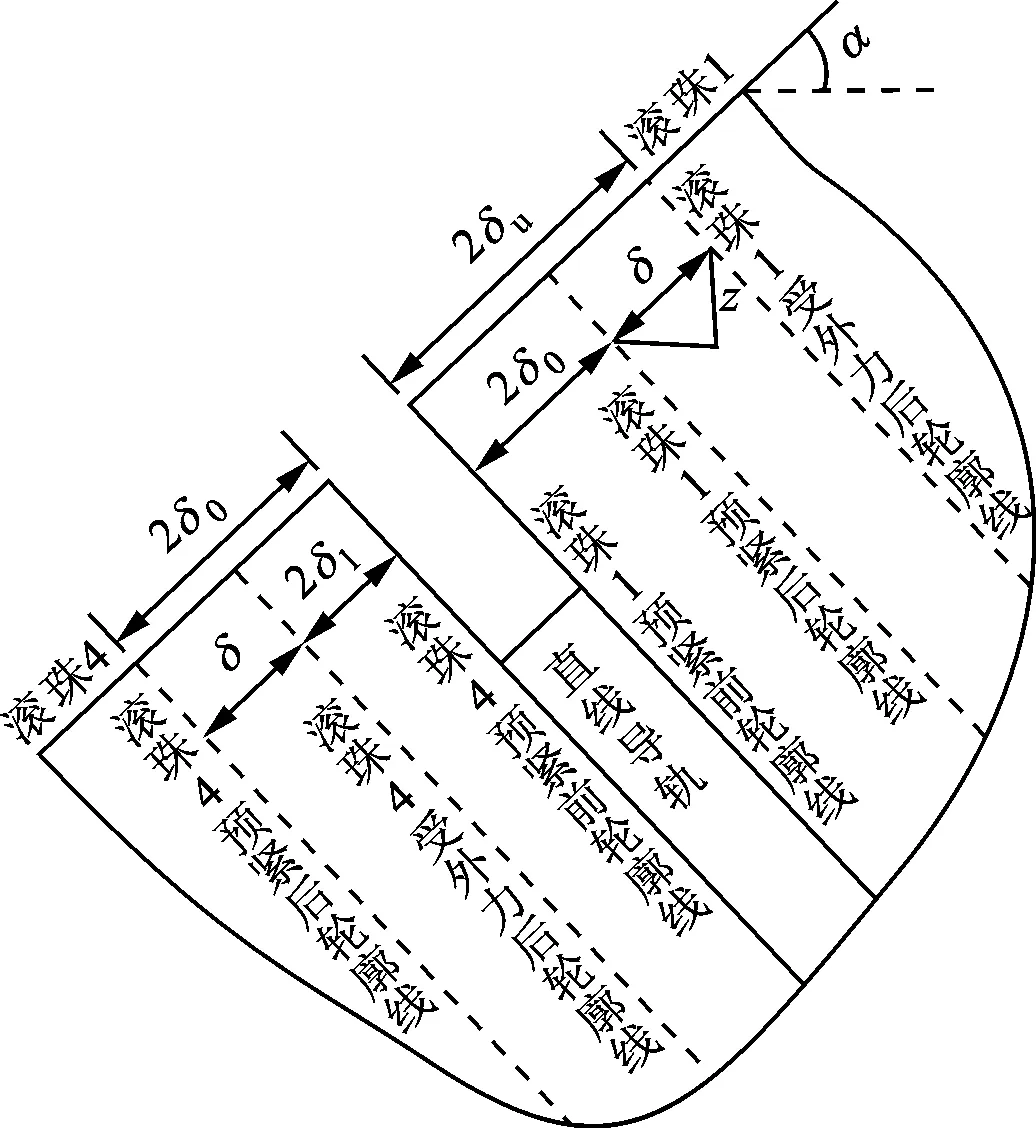
图2 滚珠1和4的变形协调情况

由图2可得

δ=2δu-2δ0=2δ0-2δl

(5)

由式(5)可得导轨副发生的垂直变形量[11]

z=δsinα=2(δu-δ0)sinα=2(δ0-δl)sinα

(6)

将式(2)～(4)代入式(5),得

(7)

(8)

(9)

将式(8)代入式(1),得

(10)

(11)

将式(9)代入式(1),得

(12)

将式(2)～(4)代入式(6),得

(13)

(14)

(15)

由式(14),得上排滚珠的接触刚度

(16)

由式(15),得下排滚珠的接触刚度

(17)

将式(11)除以式(14),得导轨副的垂直接触刚度

(18)

当F从0开始增大时,Fu也从F0开始增大(见式(10)),Fl从F0开始减小(见式(12))。当下排滚珠刚好均不受载时,有

Fl=0

(19)

将式(19)代入式(12),可求解出F,即临界力

(20)

导轨副预紧一般通过调节钢球直径来实现,而调节预紧力可以提高导轨副的初始接触力,从而提高其刚性和定位精度。预载荷等级所对应的每排滚珠所受到的总预紧力

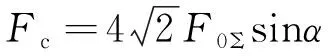
(21)

将式(20)代入式(10),得

(22)

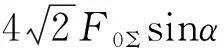
1.2 外力大于临界力时的静力学特性参数

当F>Fc时,Fl=0。将式(19)代入式(1),可得[12]

F=2NFusinα

(23)

(24)

将式(24)除以式(14),可得导轨副的垂直接触刚度

(25)

1.3 在整个外力范围内的静力学特性参数

由式(13)得

(26)

由式(10)和式(23)得

(27)

由式(8)得

(28)

由式(16)得

(29)

由式(17)得

(30)

将式(18)和式(25)合写为

(31)

2 滚动直线导轨副的数值算例

THK公司生产的SHS-35R型商业滚动直线导轨副的主要技术参数如下:滑块材料为淬透滚动轴承钢,弹性模量为206 GPa,泊松比为0.3;滚珠材料也为淬透滚动轴承钢,弹性模量为206 GPa,泊松比为0.3,半径rb=3.175 mm;直线导轨材料为感应淬火滚动轴承钢,弹性模量为206 GPa,泊松比为0.3;沟槽半径系数f=0.52,接触角为45°,沟槽数为4,每排滚珠数为12;基本额定动载荷C=62.3 kN;预载荷等级Z1所对应的总预紧力为0.01C,预载荷等级Z2所对应的总预紧力为0.04C,预载荷等级Z3所对应的总预紧力为0.07C。

2.1 预载荷等级对导轨副静力学特性的影响

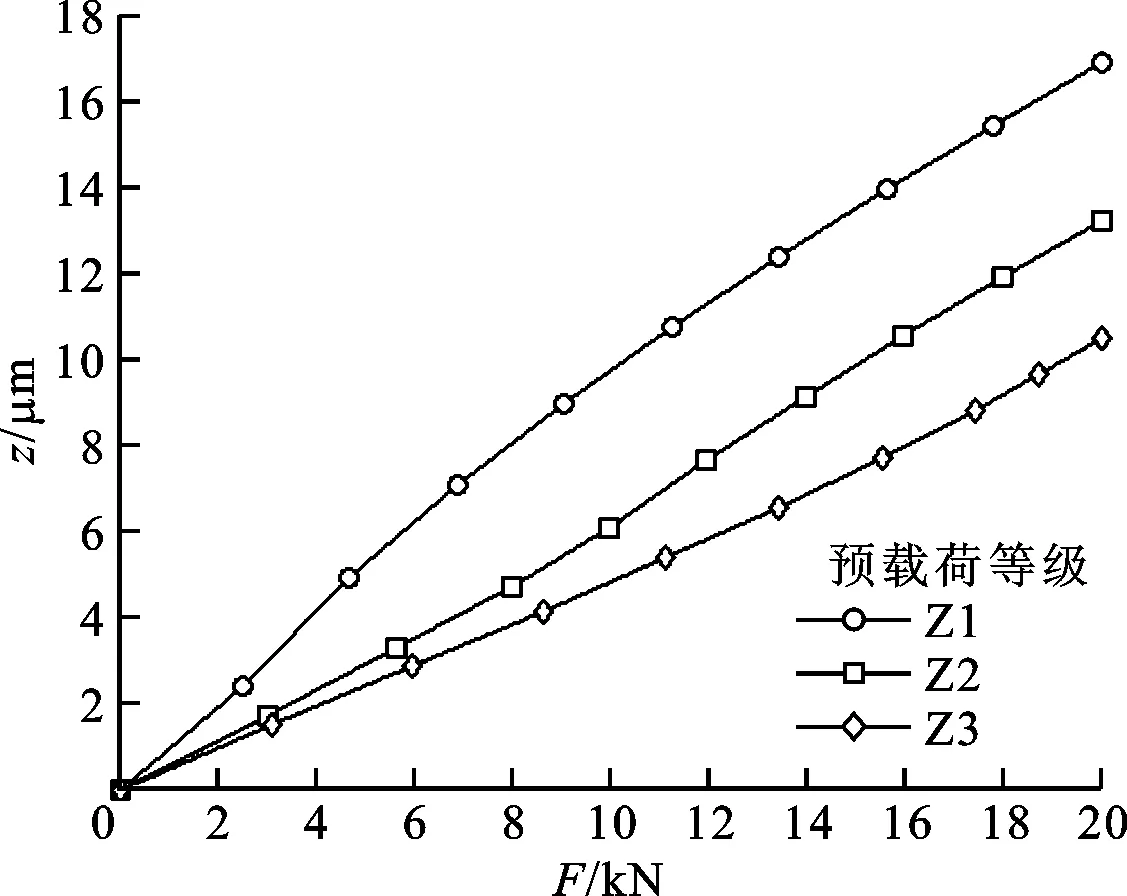
(a)导轨副的垂直变形量-外力曲线

(b)导轨副的垂直接触刚度-外力曲线图3 导轨副的静力学特性曲线

图3显示了预载荷等级对导轨副静力学特性的影响。从图3a可见,在相同的外力作用下,预载荷等级越高,导轨副的垂直变形量就越小。从图3b可见:当外力小于临界力(即每条曲线最低点所对应的横坐标,预载荷等级Z1、Z2、Z3对应的临界力分别为2 492、9 968和17 444 N)时,随外力增大导轨副的垂直接触刚度减小,因为较大的外力导致导轨副表现出明显的阻尼特性,而导轨副的垂直接触刚度随预载荷等级的提高而增大;当外力大于临界力时,随外力增大导轨副的垂直接触刚度增大,因为F使Fu线性增大(参见式(23)),最终使导轨副的垂直接触刚度k增大(参见式(25)),但导轨副的垂直接触刚度与预载荷等级无关。

2.2 预载荷等级对单个滚珠受力的影响

图4显示了预载荷等级对单个滚珠受力情况的影响。从图4a可见:随外力的增大,上排滚珠的接触压力增大;在相同的外力作用下,当外力小于临界力时,预载荷等级越高,则上排滚珠的接触压力越大(参见式(10)),而当外力大于临界力时,上排滚珠的接触压力与预载荷等级无关(参见式(23))。从图4b可见:随外力的增大,下排滚珠的接触压力减小;预载荷等级越高,下排滚珠的接触压力就越大。

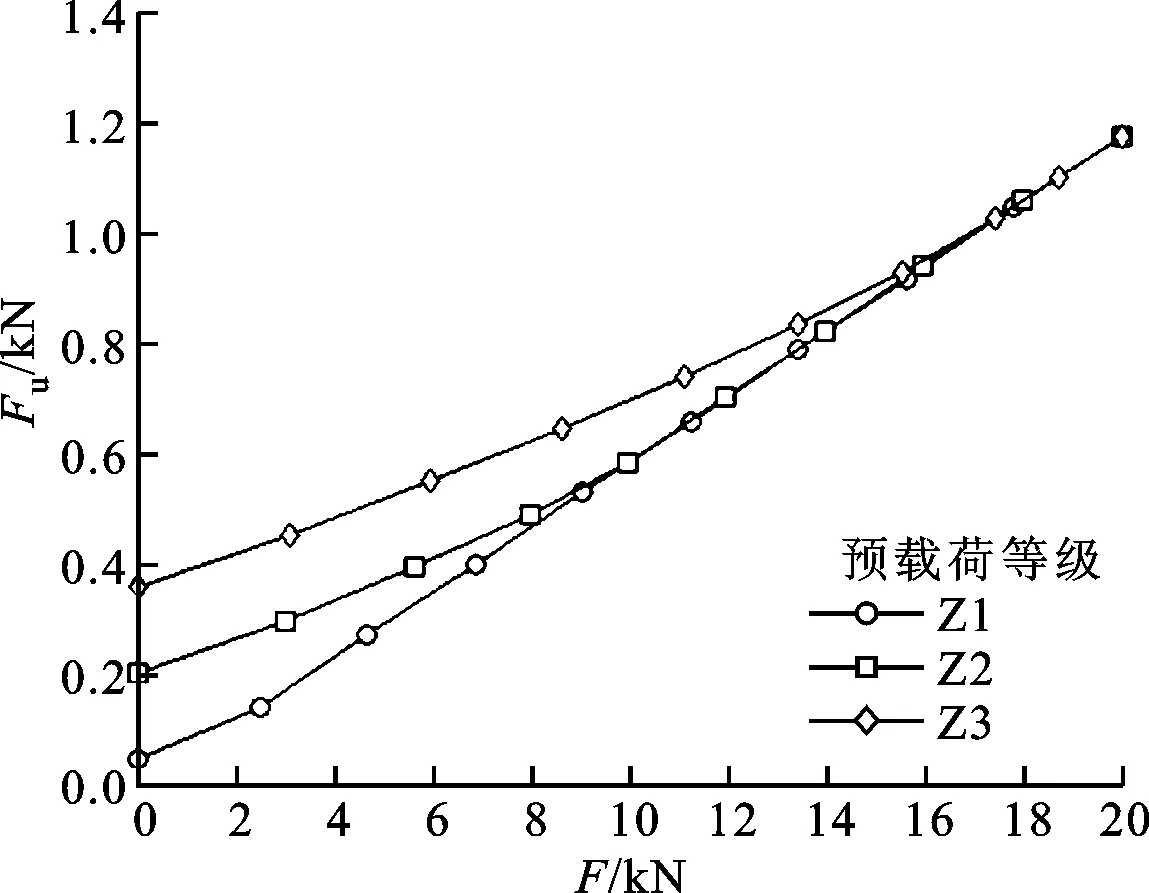
(a)上排滚珠接触压力-外力曲线

(b)下排滚珠接触压力-外力曲线图4 预载荷等级对单个滚珠受力的影响

2.3 预载荷等级对单个滚珠刚度的影响

图5显示了预载荷等级对单个滚珠接触刚度的影响。从图5a可见:随外力的增大,上排滚珠的接触刚度增大;在相同的外力作用下,当外力小于临界力时,预载荷等级越高,则上排滚珠的接触刚度越大,而当外力大于临界力时,上排滚珠的接触刚度与预载荷等级无关。从图5b可见,随外力的增大,下排滚珠的接触刚度减小。

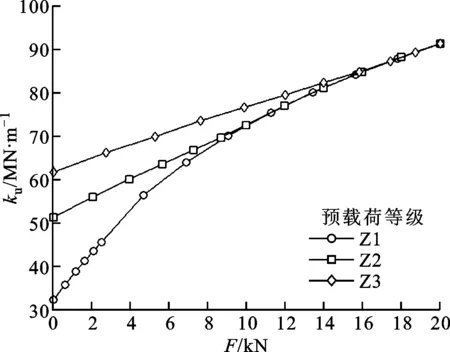
(a)上排滚珠的接触刚度-外力曲线

(b)下排滚珠的接触刚度-外力曲线图5 预载荷等级对单个滚珠接触刚度的影响

2.4 接触角对导轨副静力学特性的影响

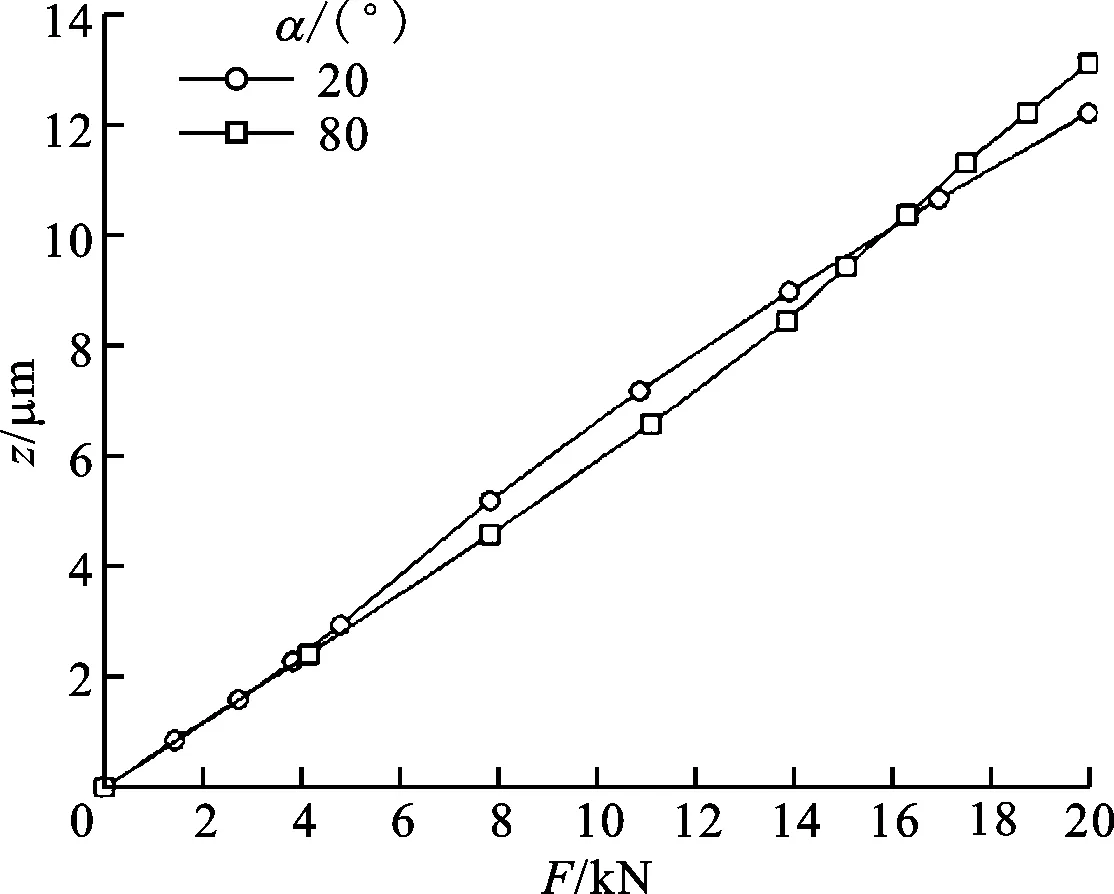
(a)导轨副的垂直变形量-外力曲线

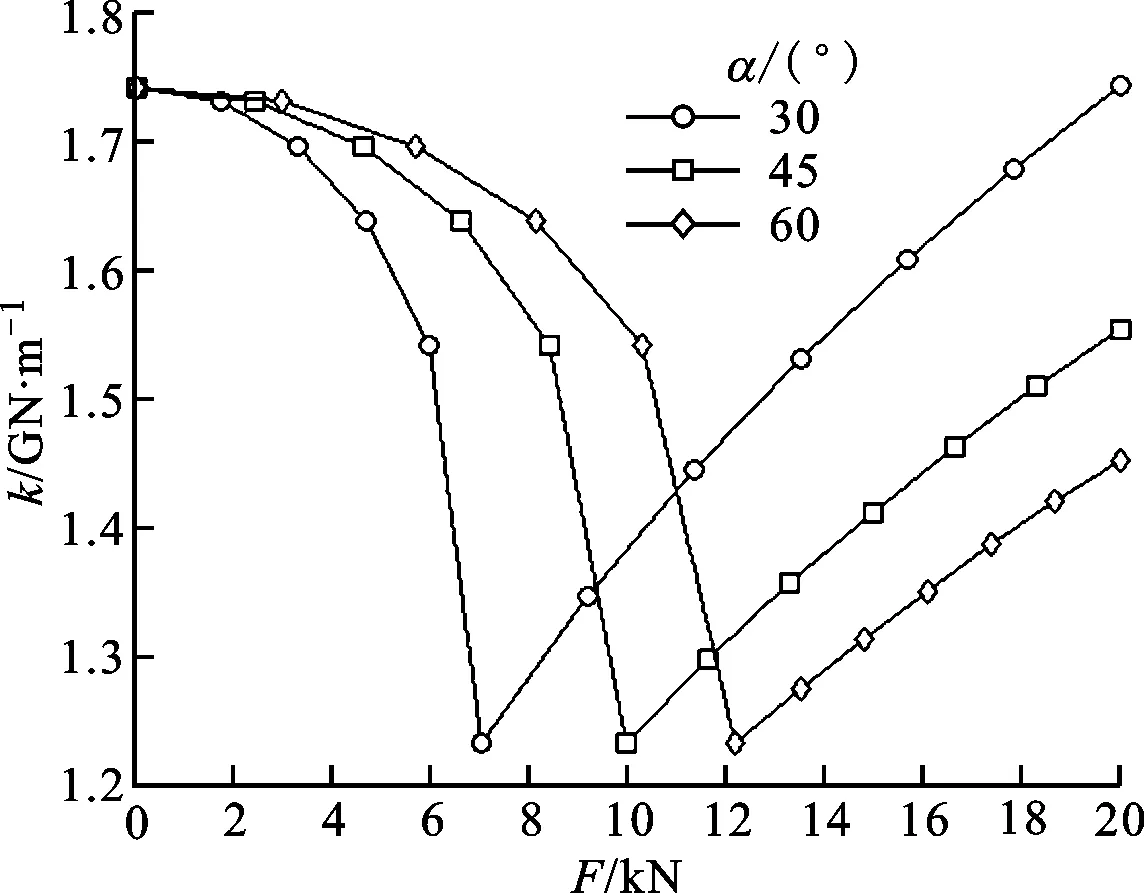
(b)导轨副的垂直接触刚度-外力曲线图6 接触角对导轨副静力学特性的影响

图6显示了预载荷等级为Z2时接触角对导轨副静力学特性的影响。从图6a可见:当外力小于临界力时,导轨副的垂直变形量随接触角的增大而减小;当外力大于临界力时,导轨副的垂直变形量随接触角的增大而增大。从图6b可见:导轨副的临界垂直接触刚度(最小值)与接触角无关(参见式(31))。

2.5 滚珠数对导轨副静力学特性的影响

图7显示了预载荷等级为Z2时每排通道沟槽的滚珠数对导轨副静力学特性的影响,从中可以看出:随滚珠数增加,导轨副的垂直变形量减小,垂直接触刚度增大。

(a)导轨副的垂直变形量-外力曲线

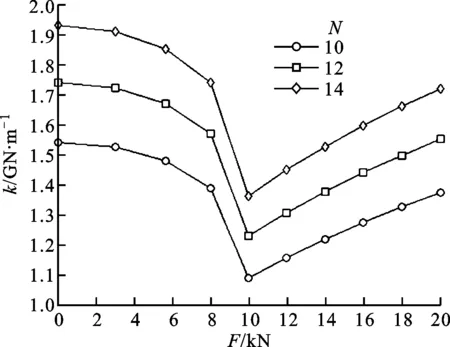
(b)导轨副的垂直接触刚度-外力曲线图7 每排沟槽滚珠数对导轨副静力学特性的影响

2.6 滚珠半径对导轨副静力学特性的影响

图8显示了预载荷等级为Z2时滚珠半径对导轨副静力学特性的影响,从中可以看出:随滚珠半径增大,导轨副的垂直变形量减小,垂直接触刚度增大。

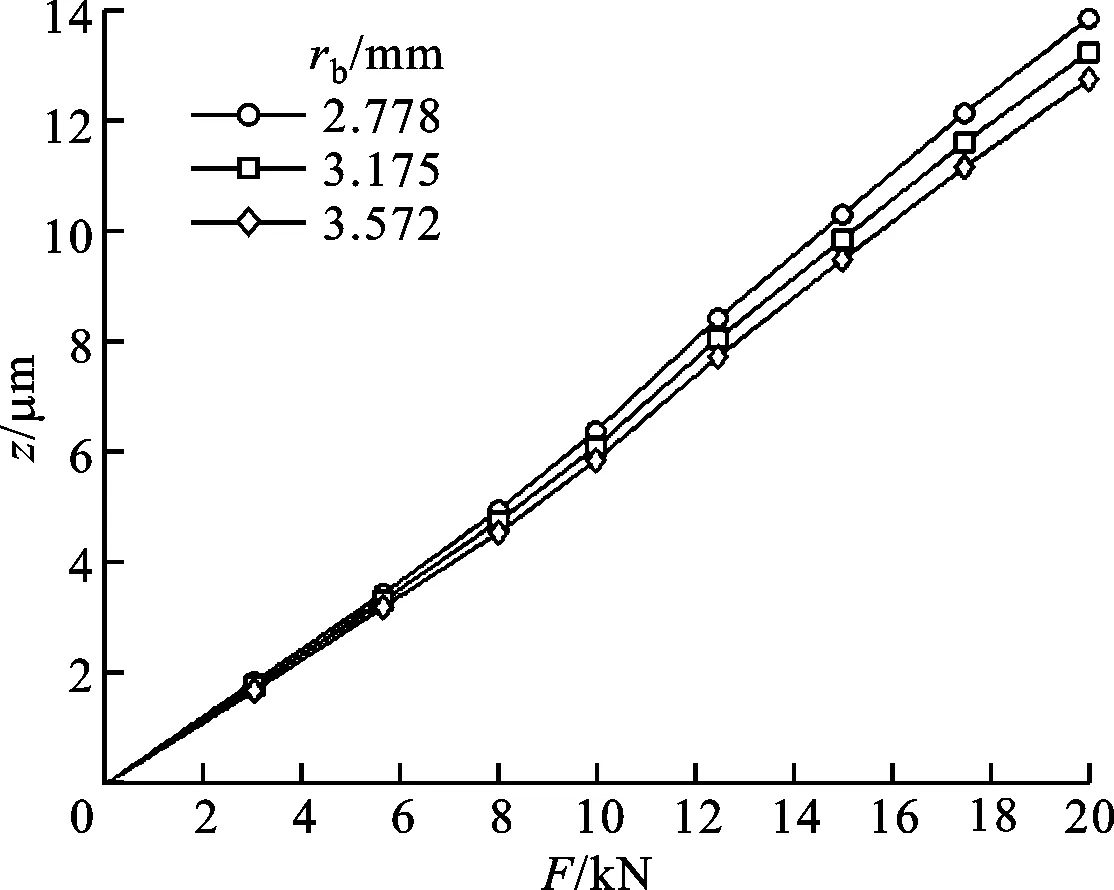
(a)导轨副的垂直变形量-外力曲线

(b)导轨副的垂直接触刚度-外力曲线图8 滚珠半径对导轨副静力学特性的影响

2.7 沟槽半径系数对导轨副静力学特性的影响

主曲率

(32)

式中:M为积分模数e的平方[13],即

M=e2,0≤e≤1

(33)

K为第一类完全椭圆积分

(34)

E为第二类完全椭圆积分

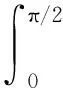
(35)

赫兹系数

(36)

主曲率与沟槽半径系数f之间的关系为

(37)

图9显示了预载荷等级为Z2时沟槽半径系数对导轨副静力学特性的影响。因为f和μ都是M的函数(涉及到第一类完全椭圆积分K和第二类完全椭圆积分E,复杂的是,这2个定积分均没有解析解),如果将M作为中间自变量,就可得到图9a。产生图9a的Matlab®R2009b程序代码见附录A(仅12行源代码),e从0增大到1,步长为0.000 1,即图9a所示的曲线有10 000个点,巧妙的是,通过源代码第3行的一个函数ellipke输出结果K和E,比文献[6]所使用的函数ellipticK和ellipticE都高效,因为函数ellipticK和ellipticE每次只能计算1个数据,且使用for和and循环结构,导致程序运行时间长。

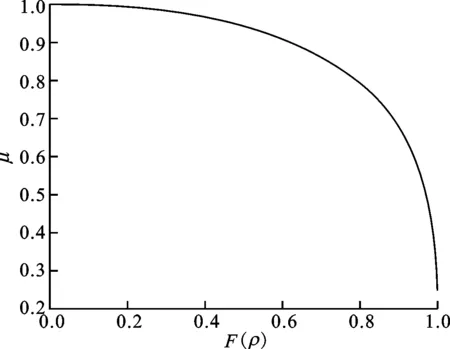
(a)赫兹系数-主曲率曲线

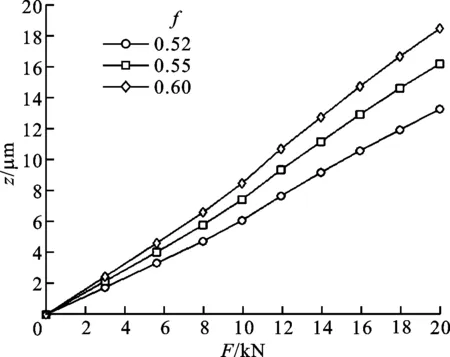
(b)导轨副的垂直变形量-外力曲线

(c)导轨副的垂直接触刚度-外力曲线图9 沟槽半径系数对导轨副静力学特性的影响

根据图9a和式(37),可建立μ与f之间的函数关系。例如:当f=0.52时,μ=0.634 4,不同于文献[8]的μ=0.634和文献[11-12]的μ=0.634 1;当f=0.60时,μ=0.850 7。由图9a可知:当F(ρ)=0.833 1时,μ=0.762 1;当F(ρ)=0.833 6时,μ=0.761 5。因此,当f=0.55,即F(ρ)=0.833 3时,用线性插值法[14]可求得赫兹系数

(0.833 3-0.833 1)=0.761 9

同理,根据图9a可知,当F(ρ)=0.908 8时,μ=0.665 7,当F(ρ)=0.909 5时,μ=0.664 5,故当f=0.525,即F(ρ)=0.909 1时,用线性插值法可求得赫兹系数

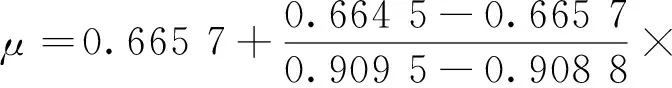
这与文献[9]中的μ=0.665也有所不同。

从图9b可见,导轨副的垂直变形量随沟槽半径系数的增大而增大;从图9c可见,导轨副的垂直接触刚度随沟槽半径系数的增大而减小。

2.8 本文计算结果的验证

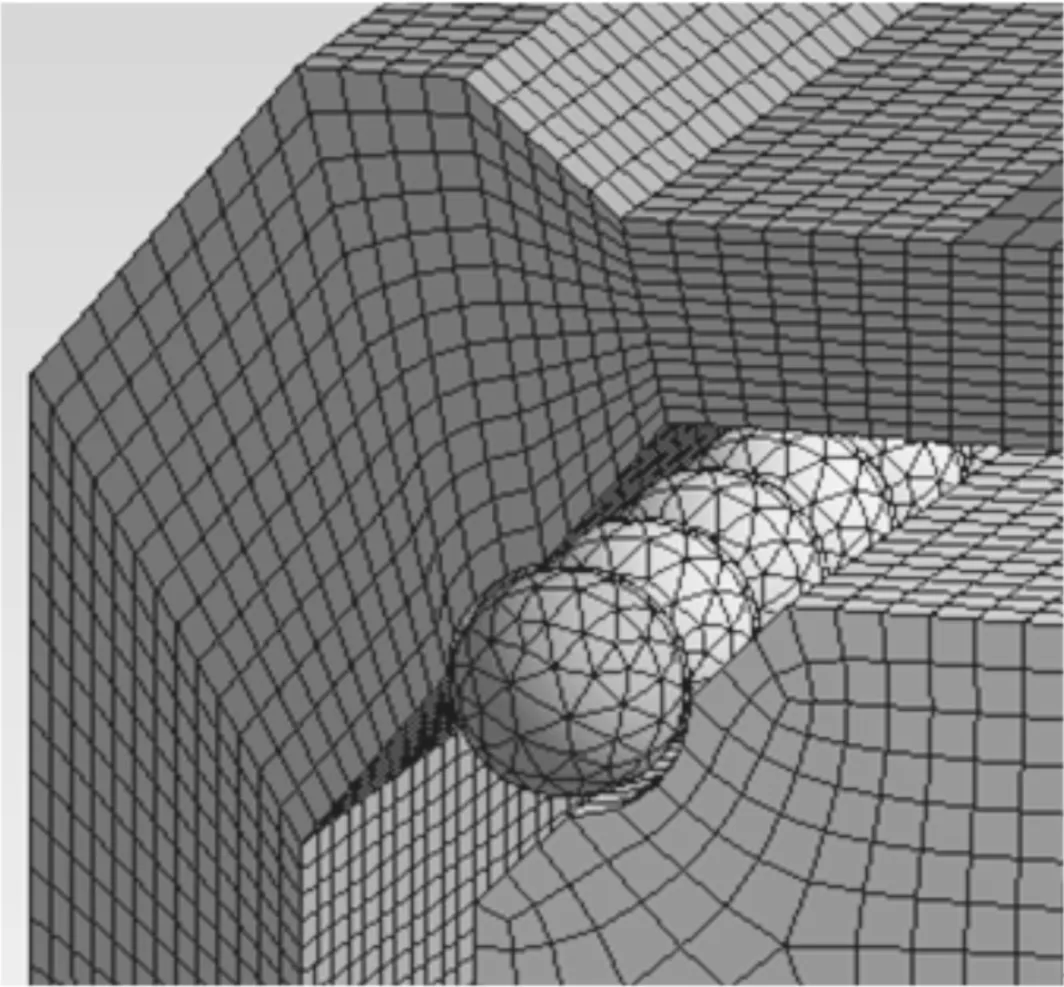
(a)划分网格后的导轨副

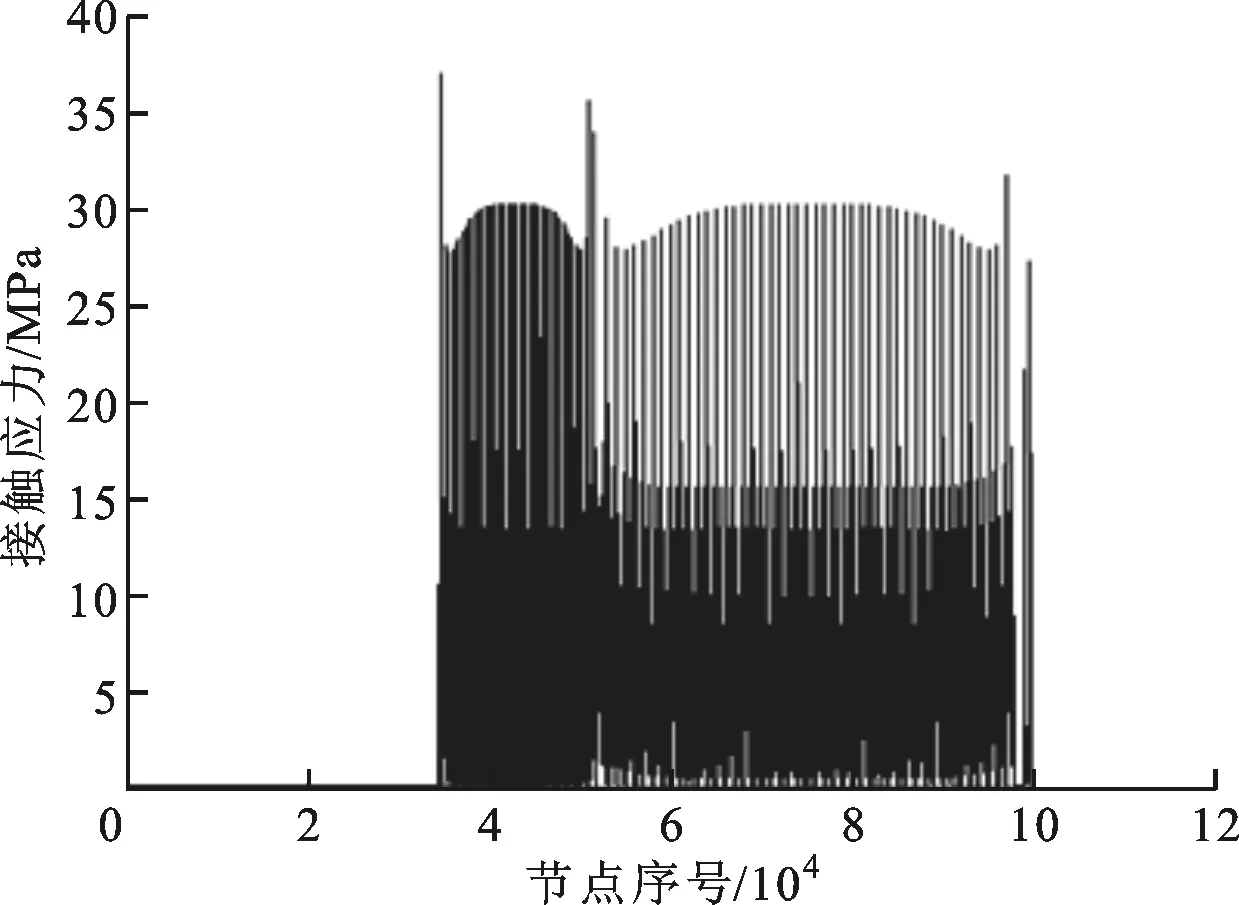
(b)滚珠与滚道的接触应力

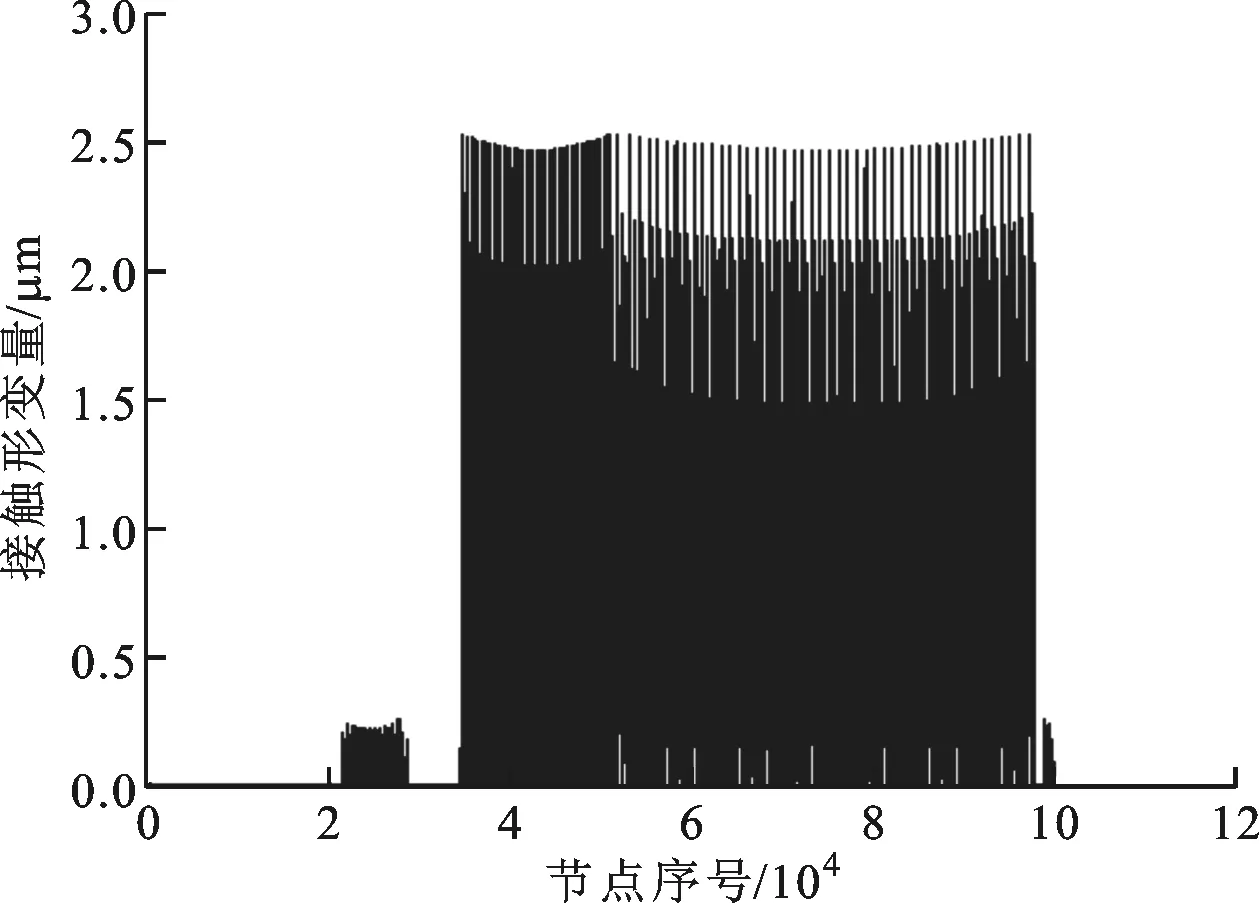
(c)滚珠与滚道的接触变形量

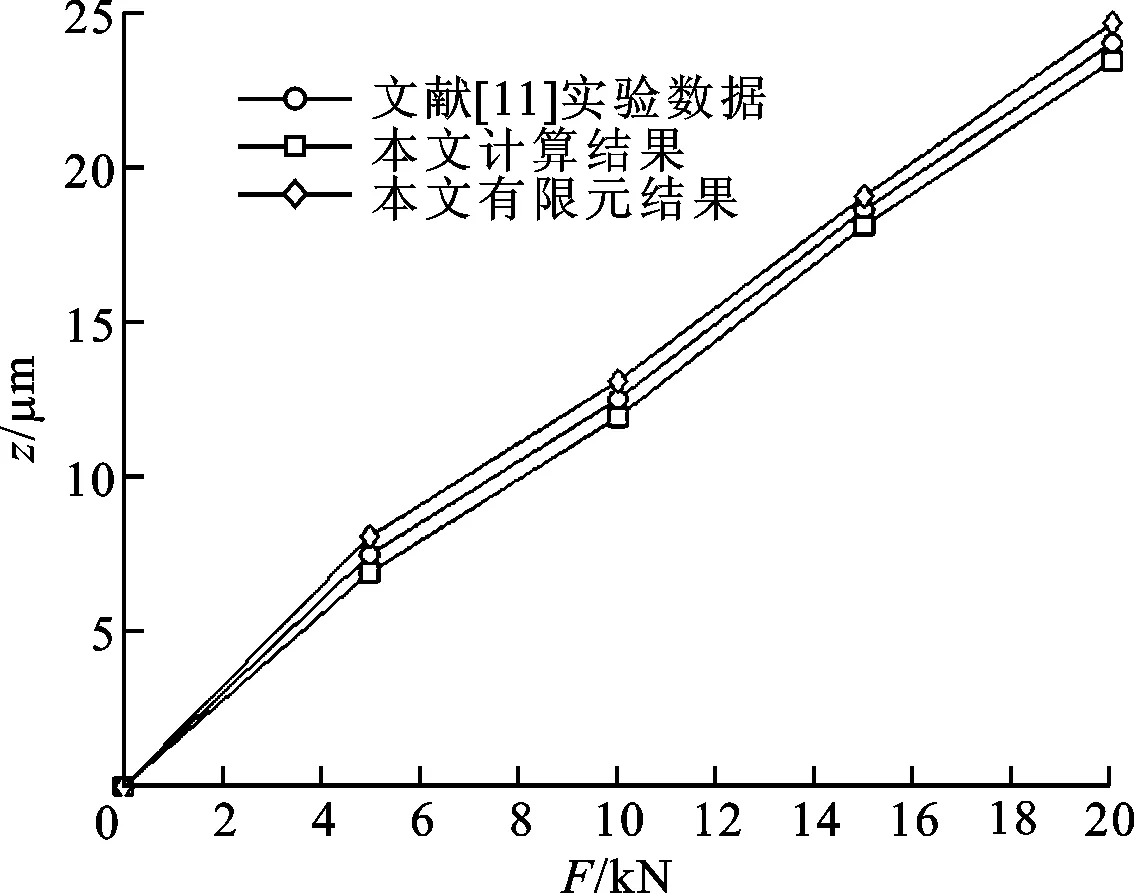
(d)导轨副的垂直变形量-外力曲线

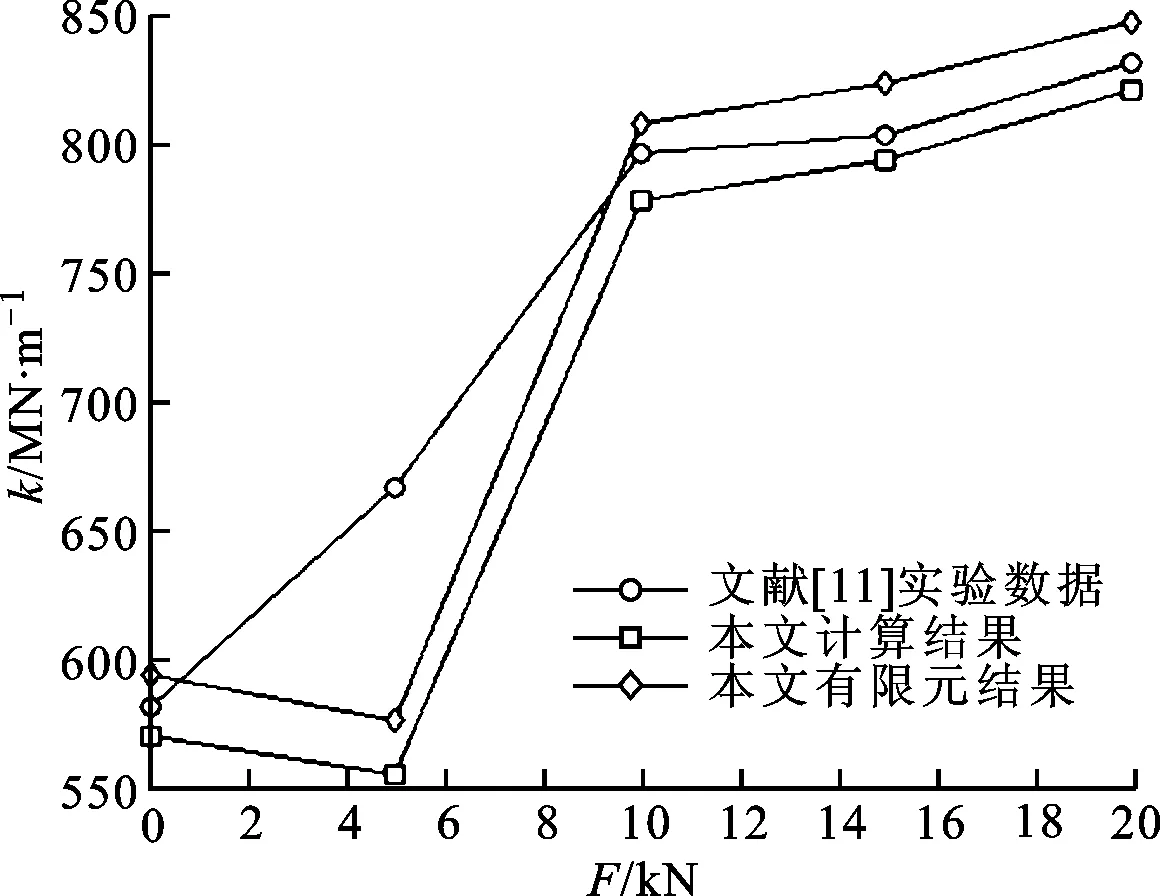
(e)导轨副的垂直接触刚度-外力曲线图10 本文计算结果与实验结果的比较

为验证本文计算结果的正确性,建立了导轨副的有限元模型,网格划分如图10a所示。本文计算结果以及与其他文献结果的比较见图10(图10b、10c所示的曲线都有100 316个点)。从图10b可见,滚珠与滚道之间的接触应力小于40 MPa。从图10d可见,本文计算的导轨副垂直变形量略小于实验值,而采用有限元法所得的导轨副垂直变形量略大于实验值。从图10e可见,本文计算的导轨副垂直接触刚度在轻载时与实验值相差较大,这主要是因为文献[11]中只有5个实验数据(F分别为0、5、10、15、20 kN,0≤F/kN≤5属于轻载,5

3 结 论

本文考虑滚珠与滑块、直线导轨沟槽同时接触,计算了滚珠的接触变形量,对导轨副轻载时的多种静力学特性参数进行了改进计算,推导了导轨副重载时的各种静力学特性参数,获得的具体结论如下。

(1)导轨副的垂直变形量随预载荷等级的降低,滚珠数、滚珠半径的减小或沟槽半径系数的增大而增大。

(2)导轨副的垂直接触刚度随滚珠数、滚珠半径的增大或沟槽半径系数的减小而增大。当外力小于临界力时,导轨副的垂直接触刚度随外力的增大而减小,随预载荷等级的提高而增大;当外力大于临界力时,导轨副的垂直接触刚度随外力的增大而增大。

(3)上排滚珠的接触压力随外力的增大而增大。当外力小于临界力时,上排滚珠的接触压力随预载荷等级的提高而增大;当外力大于临界力时,上排滚珠的接触压力与预载荷等级无关。下排滚珠的接触压力随外力的增大或预载荷等级的降低而减小。

(4)上排滚珠的接触刚度随外力的增大而增大。当外力小于临界力时,上排滚珠的接触刚度随预载荷等级的提高而增大;当外力大于临界力时,上排滚珠的接触刚度与预载荷等级无关。下排滚珠的接触刚度随外力的增大而减小。

附录A 生成图9a的Matlab程序代码

e=0:0.0001:1;

M=e.∧2; %式(33)

[K,E]=ellipke(M); %式(34)和式(35)

F=1+2*(1-M)./M.*(E-K)./E; %式(32)

mu=2*K/pi.*(pi*(1-M)./(2*E)).∧(1/3);

%式(36)

plot(F,mu,‘-black’,‘LineWidth’,1) %黑色实线,线宽为1 point

set(gca,‘XTickLabel’,{0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ‘1.0’}) %在小竖线下面标注数值

set(gca,‘YTickLabel’,{0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ‘1.0’})

box off %使当前坐标框敞开

xlabel(‘itF m(itρ m)’) %it为斜体,rm为正体

ylabel(‘itμ’)

set(gcf,‘color’,‘white’) %使当前坐标框外部的颜色为白色