双金属复合管直角法兰双辊夹持旋压起皱分析

范淑琴,王琪,华毅,赵升吨,赵永强

(西安交通大学机械工程学院,710049,西安)

近年来,随着经济的发展能源需求急剧增长,许多国家都在大量开采石油、天然气,因此在油气田高腐蚀环境下应用的管材的数量也迅速增加。采用传统的不锈钢类或高合金类耐腐蚀管材成本较高,而采用普通钢管材虽然成本低,但耐腐蚀性能差。双金属复合管的内复层为不锈钢,可满足高腐蚀环境输送介质的要求,外层为普通碳钢,可满足管材的机械性能要求,这样既兼顾了内、外两层管材的优点,同时又大大减少了管材的成本,具有良好的性能和广泛的应用前景。双金属复合管在应用时往往需要焊接连接,其焊缝处的抗环境开裂能力以及耐蚀性是双金属复合管安全使用寿命的重要影响因素之一,然而双金属复合管的基层和复层是不同的金属,具有不同的特点和性能,需要对基层和复层分别焊接,这是传统焊接无法解决的[1]。

目前,国外掌握先进连接技术的公司,例如芬兰的GS-Hydro公司,采用非焊接方式连接单金属管路,以解决单金属管焊接连接技术连接强度低、可靠性差的问题,即先对管接头处进行预加工,然后采用标准连接配件进行连接。需要预加工的管接头主要有应用于中压系统和中低压系统的37°和90°扩口法兰,以及用于高压系统的保护环法兰。在石油化工、环保、水利水电等行业用来运输液体的管道所承受的压力基本上属于中压或中低压,因此37°和90°扩口法兰的应用更为广泛。

目前的先进技术是采用旋压成形对管端进行旋压翻边得到扩口法兰。图1所示为GS-Hydro公司采用旋压技术得到的90°扩口法兰[2-3],但该公司采用的旋压技术主要应用于不锈钢和普通碳钢等单金属材料管道连接法兰的加工,并不包括双金属复合管连接法兰的加工。为了解决双金属复合管焊接法兰的问题,有必要开展双金属复合管的管接头法兰旋压翻边成形机理的研究。

图1 GS-Hydro公司的90°扩口法兰[2]

本课题组曾开展过单金属的双辊夹持旋压成形技术研究[4-8],图2所示为双辊夹持旋压成形原理示意图。在旋压成形前,将筒形件毛坯套装在内胀式夹具上,该夹具在轴向压力的作用下沿径向胀开,实现成形过程中夹紧毛坯的作用,同时2个旋辊夹住预成形的法兰部位,并施加翻边力。在旋压成形过程中,毛坯随着夹具一起旋转,而2个旋辊在自转的同时还在旋压头的带动下作3个自由度的运动——沿z轴的直线运动、沿x轴的直线运动和绕y轴的转动,其中沿z轴和x轴的直线运动配合完成90°的圆弧,绕y轴的转动实现90°的翻边,3个自由度运动的配合使得2个旋辊夹持板料绕一个定点旋转90°,实现直角法兰的成形。

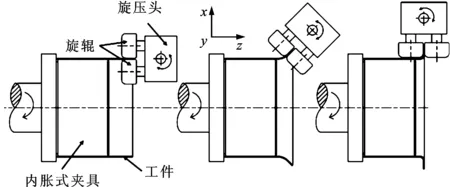
(a)成形前 (b)成形中 (c)成形后图2 双辊夹持旋压成形原理示意图

双辊夹持旋压成形属于普旋的范畴,因此它具有普旋的优点,即成形力和成形载荷容量小,设备成本低,所得到的零件机械强度高,表面质量好[9-12]。除此之外,双辊夹持旋压成形还具有一些本质上区别于普通旋压的优点:双辊夹持旋压成形工艺采用2个形状简单的圆柱体旋辊对板料进行对称夹持,不易起皱,旋压件的尺寸精度高;板料与旋辊为线接触,载荷作用面积大,每道次的变形程度大,旋压生产效率高;法兰边的形状与芯模的外形轮廓无关,而是由旋辊的运动轨迹决定,属于无模、柔性旋压成形,可以实现包括90°法兰等多种形状的法兰成形。

本文将双辊夹持旋压成形方法应用于双金属复合管管端90°扩口法兰的成形,采用有限元仿真分析的方法对双金属复合管90°扩口法兰双辊夹持旋压成形机理进行研究,首先建立内层为304不锈钢、外层为Q235普通钢的双金属复合管的双辊夹持旋压成形有限元模型,通过有限元仿真模拟,分析Q235普通钢/304不锈钢复合管在双辊夹持旋压成形过程中的起皱缺陷形式及其影响因素,获得主要工艺参数对起皱的影响规律和一定径厚比条件下的法兰宽度极限值,以期为双辊夹持旋压成形技术应用于双金属复合管法兰成形提供依据。

1 双辊夹持旋压成形有限元模型

采用非线性有限元分析软件ABAQUS/Explicit建立双辊夹持旋压成形有限元分析模型,如图3所示。为了便于分析,在有限元模型中做如下假设和简化:①变形材料是均一、各向同性和不可压缩的;②旋辊和内胀式夹具为刚体,不发生变形;③忽略变形中的温度效应,将变形假设为等温变形。

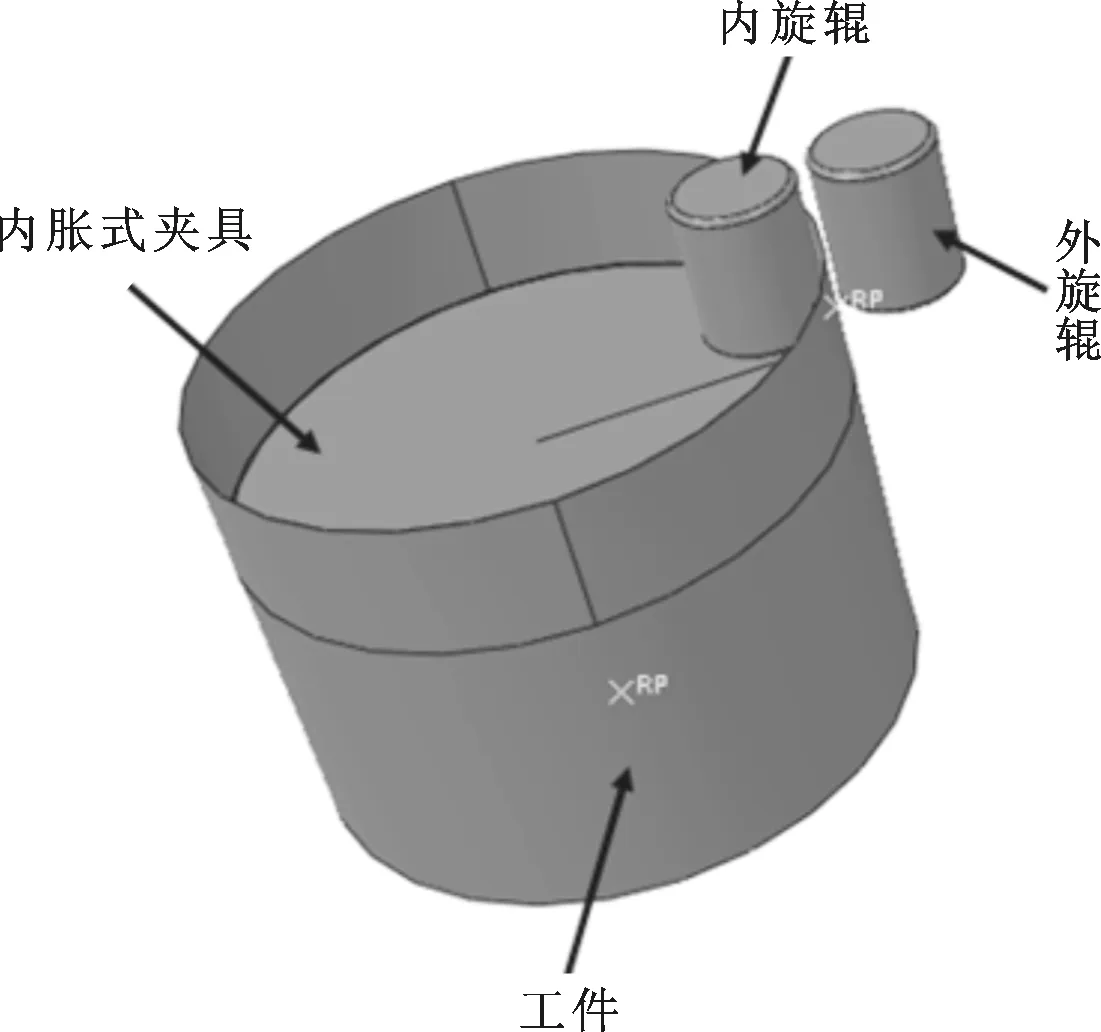
图3 双辊夹持旋压成形有限元模型

1.1 几何模型

双金属复合管直角法兰双辊夹持旋压成形的几何模型如图4所示,由坯料、内胀式夹具、内旋辊和外旋辊4个部分组成。在成形过程中,旋辊夹持住坯料并绕一个定点转动,该定点即为模拟中的旋辊参考点Rp。最终成形的法兰宽度由内外旋辊夹持的长度所确定。在几何模型中,c为旋辊参考点Rp与夹具夹持位置之间的距离,p为参考点Rp到旋辊底部的垂直距离,e为2个旋辊之间的间距,初始毛坯壁厚t0为基层板厚t1和复层板厚t2之和。双辊夹持旋压成形直角法兰几何模型的参数值见表1。

为了避免外旋辊在成形后期与工件干涉,参考点到旋辊底面的距离p应该大于t0/2,否则在成形后期外旋辊将穿透到工件内部,但p的取值也不能太大,否则成形法兰的尺寸精度将大大降低。在实际加工中,p应该在满足大于t0/2的条件下尽量取较小值[6]。本文的毛坯初始壁厚t0为2 mm,p取2 mm。

双辊夹持旋压成形与普旋中的旋辊运动不太相同,为了之后方便分析工艺参数的影响规律,定义双辊夹持旋压成形中的旋辊进给率f为工件绕主轴旋转1圈时,旋辊翻边的弧度。例如,在时间T内坯料旋转N圈,旋辊翻边90°,则此时的旋辊进给率为(π/2N) rad/r。本文模型保持夹具的转速不变,通过改变旋辊翻边90°时夹具转过的圈数,即旋辊的翻边速度,从而改变旋辊的进给率。

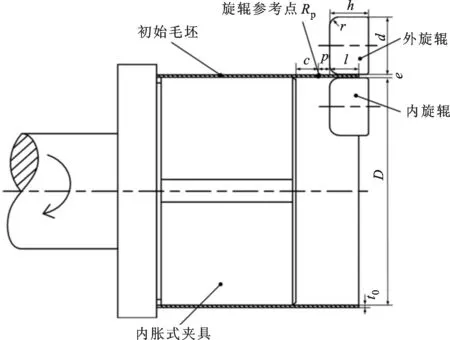
图4 双辊夹持旋压成形的几何模型

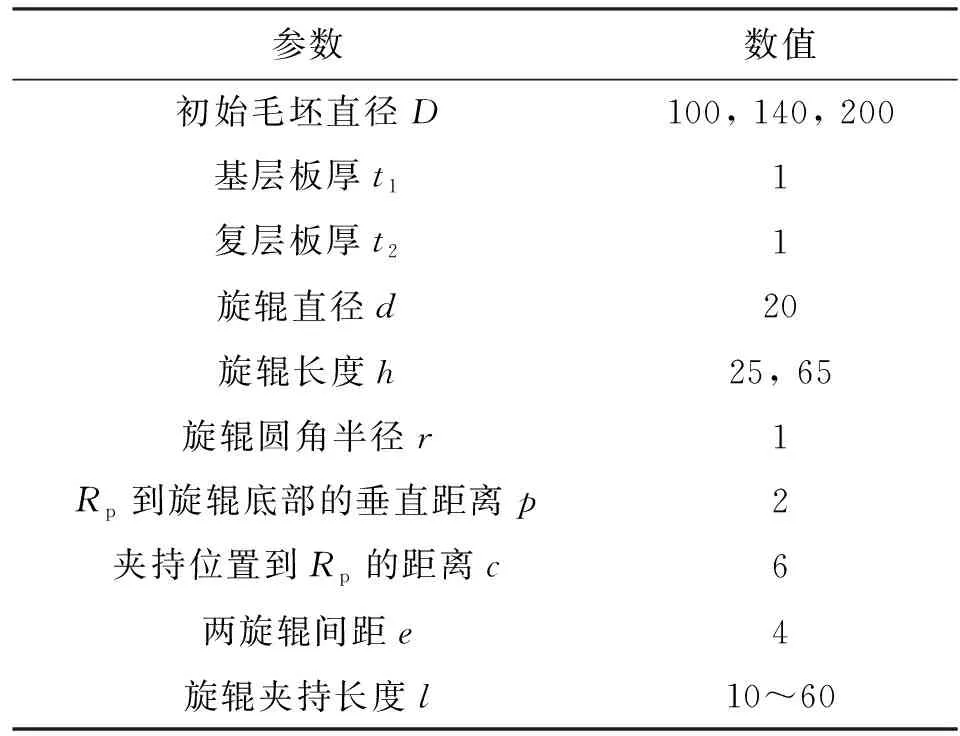
表1 双辊夹持旋压成形双金属复合管直角法兰的几何模型参数 mm

1.2 材料模型

双金属复合管在宏观上可以看作是一个整体,从微观上可视为具有不同材料属性的层与层的叠加,因此复合管的建模有2种模型:一种是整体模型,另一种是分层模型[13]。夏琴香教授课题组对这2种模型进行了不锈钢/铝/不锈钢3层复合板拉深成形数值模拟,发现分层建模比整体建模更为准确。因此,本文的材料模型也采用分层建模,首先通过材料性能试验获得Q235普通钢和304不锈钢2种金属材料的应力-应变关系曲线,如图5和图6所示,然后在有限元模型里分层赋予坯料的材料属性(见表2)。

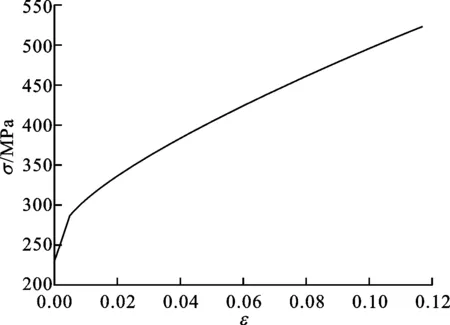
图5 304不锈钢的真实应力-应变曲线

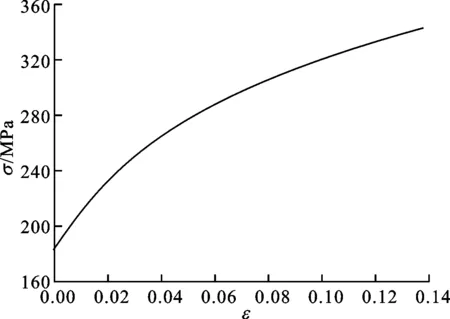
图6 Q235普通钢的真实应力-应变曲线

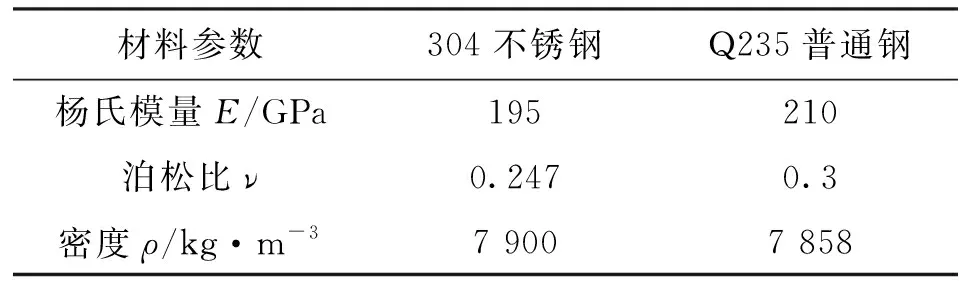
材料参数304不锈钢Q235普通钢杨氏模量E/GPa195210泊松比ν0.2470.3密度ρ/kg·m-37 9007 858

1.3 接触关系和边界条件

在双金属复合板双辊夹持旋压成形中,需要设置不同部件之间的接触关系,本文设置内旋辊与坯料内表面间的接触对、外旋辊与坯料外表面间的接触对以及夹具外表面和坯料内表面间的接触对。同时,还设置了坯料和夹具之间的Tie约束,以实现坯料随着夹具的转动而转动。之后,对内旋辊与坯料内表面间的接触对、外旋辊与坯料外表面间的接触对的摩擦因数进行设置,摩擦因数取0.3;夹具外表面和坯料内表面间的接触对设置为无摩擦。

在Load模块中进行边界条件设定,根据旋辊运动轨迹来定义幅值曲线和设置边界条件。在变形过程中,坯料随着夹具的转动而转动,故对于旋辊而言,运动轨迹的设置较简单,只需在旋辊参考点上设置旋辊绕y轴的角速度,在夹具参考点上设置夹具绕z轴转动的角速度,便可完成对于旋辊轨迹的设定。

1.4 网格划分

将内胀式夹具视为离散刚体,采用R3D4单元来进行网格划分。由于夹具在变形过程中未发生变形,故为了提高计算效率,对夹具采用较大的网格单元。将旋辊也看作是离散刚体,同样采用R3D4单元来进行网格划分。由于旋辊在成形时与坯料变形区接触,所以旋辊的网格单元设得较小,同时在它的圆角处细化网格,以保证模拟的精确性。将坯料定义为变形体,故使用S4R单元来划分网格,并在其变形区进行网格细化,此外还采用了Enhanced沙漏控制。

2 有限元模型验证

在有限元模型中设置了工件和夹具的Tie约束,以实现工件随夹具的转动而转动,所以采用动态显式有限元进行计算时,夹具转速对模拟的动态效应影响很大。一般用系统的动能和内能之比γ来衡量系统的动态效应,γ不大于5%则认为系统的动态效应对有限元模拟结果没有影响,可以保证模拟的准确性。

在有限元模拟时,分析了夹具转速对动态效应的影响。在保证进给率不变,即坯料旋转20圈后翻边90°的条件下,设定不同的分析步时间(step time)来获得不同的夹具转速,当step time分别取0.5、1、2 s时,夹具转速n分别为251.2、125.6、62.8 rad/s。通过有限元模拟,获得了不同夹具转速下系统的动态效应变化曲线,如图7所示。

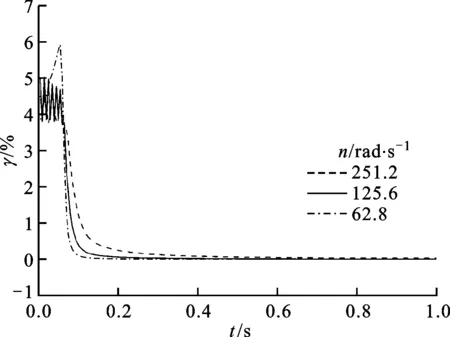
图7 不同夹具转速下的坯料动内能比变化

由图7可以看出,在不同的夹具转速下,γ值最后都稳定在了一定的范围内,不大于5%,并且n=125.6 rad/s时的γ值比n=251.2 rad/s时的γ值降低了很多,但与n=62.8 rad/s时的γ值相差不大。考虑到计算时间,选择夹具转速n=125.6 rad/s,这样既能保证模型的准确性,也可以使计算更有效率。

3 结果与讨论

3.1 起皱形式

3.1.1 旋辊进给率引起的起皱 在夹具转速为125.6 rad/s、旋辊圆角半径为1 mm、旋辊夹持坯料的长度为10 mm时,分别取旋辊进给率为0.039、0.051、0.079、0.157、0.314和1.57 rad/r进行了双辊夹持旋压成形数值模拟,分析了旋辊进给率对双辊夹持旋压成形转矩和成形质量的影响规律。

图8所示为不同旋辊进给率f对应的工件成形结果,从中可以看出:当f=1.57 rad/r时,模型的法兰边成形不完全,故f要在小于1.57 rad/r的范围内选择;当f=0.314,0.157 rad/r时,模型的法兰边都出现了不同程度的起皱;当f=0.079,0.051,0.039 rad/r时,模型的法兰边较为平整,无起皱现象。因此,为了保证法兰不起皱,旋辊进给率应小于0.157 rad/r。

(a)f=1.57 rad/r(b)f=0.314 rad/r(c)f=0.157 rad/r

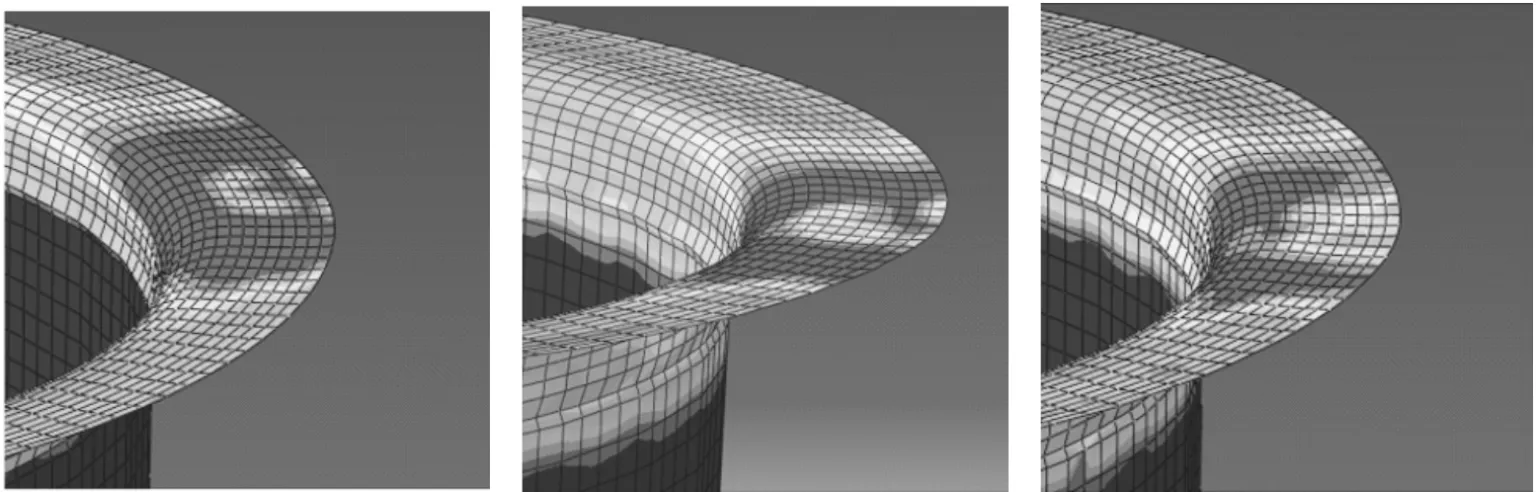
(d)f=0.079 rad/r(e)f=0.051 rad/r(f)f=0.039 rad/r图8 不同进给率下的成形计算结果

在保持夹具转速为125.6 rad/s不变的条件下,不同的旋辊进给率所对应的成形时间不相同,为了方便分析比较不同进给率对成形转矩的影响,成形过程用百分数表示。图9所示为不同旋辊进给率下双辊夹持旋压成形过程中成形转矩的变化曲线,从中可以看到,随着成形过程的进行,成形转矩先急剧增大后保持平稳,而且随旋辊进给率增加,成形转矩也相应增大。

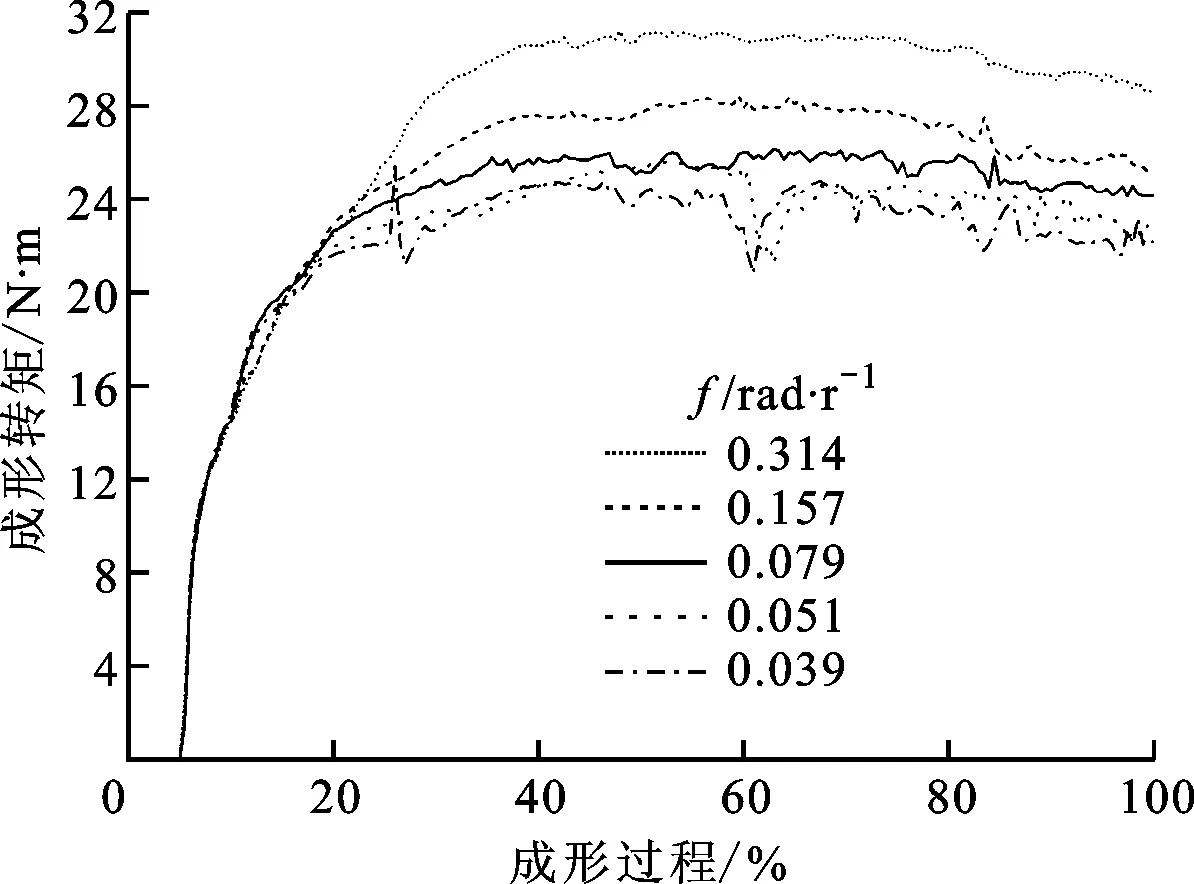
图9 旋辊进给率对成形转矩的影响

由图10可以看出,随着旋辊进给率的增大,最大壁厚差先减小后增大,这是由于在大的旋辊进给率下,最后得到的工件法兰部分的不均匀程度以及最大壁厚差都会变小,即工件的最终成形质量和精度变好,但是旋辊进给率也不能无限增大,当旋辊进给率大到一定程度后,就会使得法兰边出现起皱现象。综合考虑,本文最终选择旋辊进给率为0.079 rad/r。

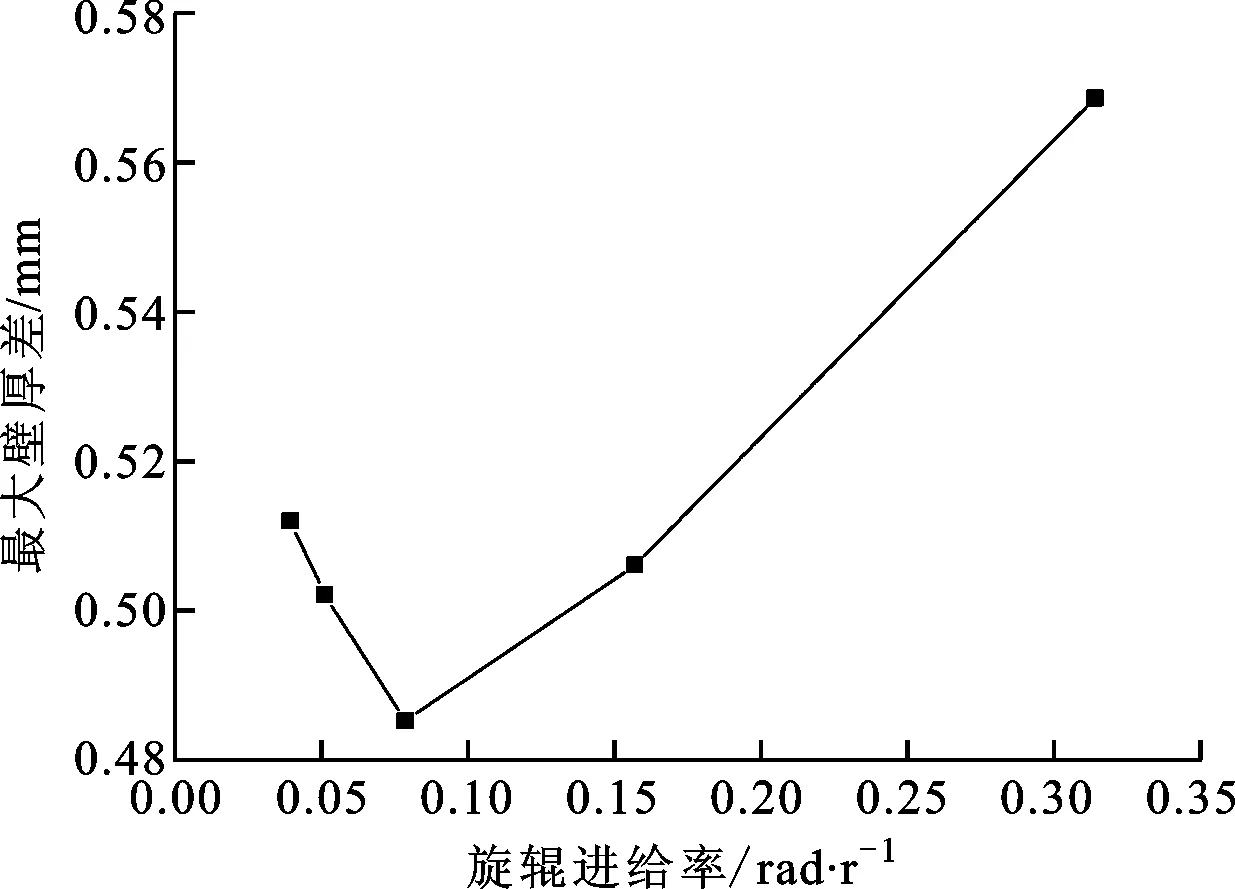
图10 旋辊进给率对工件最大壁厚差的影响

3.1.2 不同径厚比引起的起皱 采用基层板厚和复层板厚均为1 mm,总壁厚为2 mm,内径分别为100、140和200 mm的Q235普通钢/304不锈钢复合管毛坯进行双辊夹持旋压成形仿真分析,毛坯径厚比分别为50、70和100。旋辊的几何参数按照表1选取。表1中有2种规格的旋辊,其直径均为20 mm,但长度分别为25和65 mm。成形的法兰宽度不大于25 mm时采用长度为25 mm的旋辊,而成形的法兰宽度大于25 mm、小于65 mm时采用长度为65 mm的旋辊。夹具转速取125.6 rad/s,旋辊进给率取0.079 rad/r,分析坯料的径厚比对双辊夹持旋压成形的影响规律。由图11可以看出,随着坯料内径的逐渐增大,旋压成形所需转矩逐渐变小,这说明随着径厚比的增大,工件成形变得更加容易。

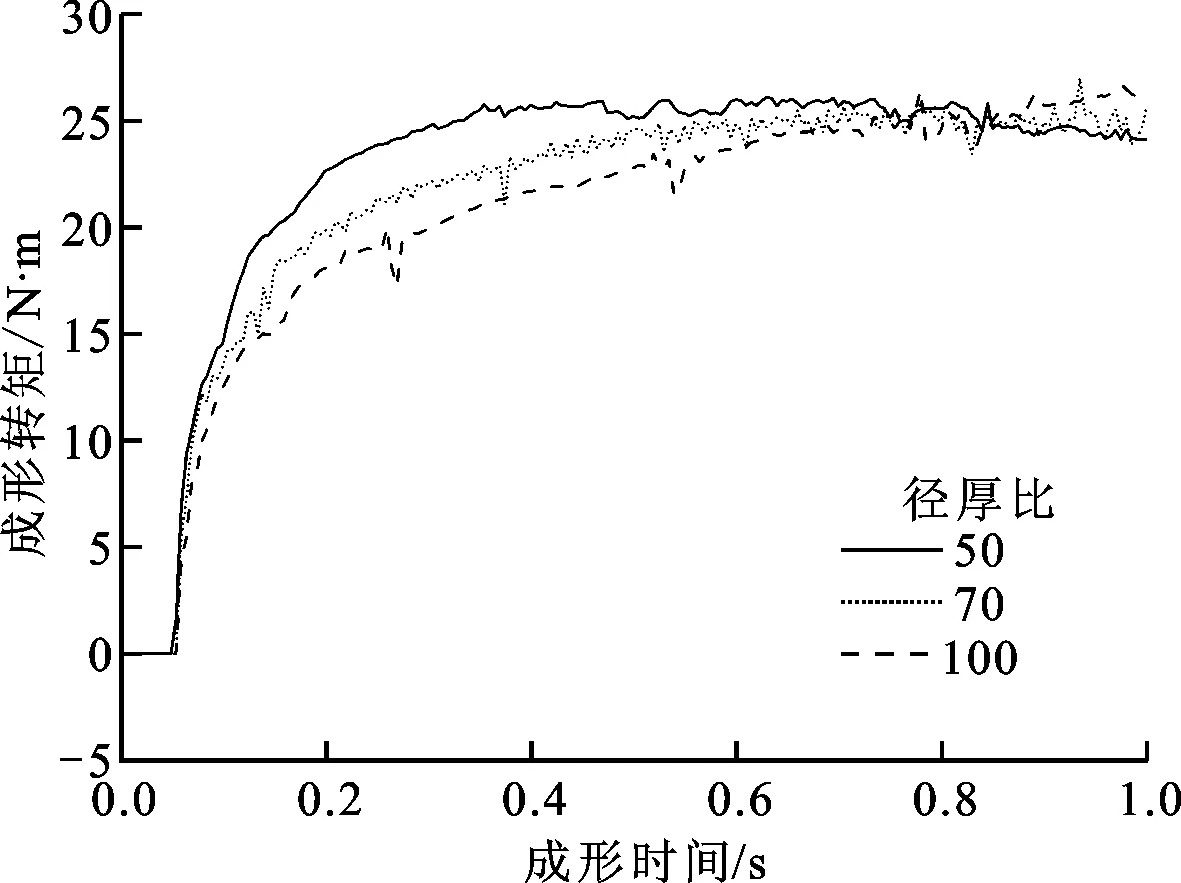
图11 不同径厚比、法兰宽度10 mm时的成形转矩

图12所示是径厚比为50的工件的成形结果,可见翻边宽度b为25 mm时得到的工件最外缘较为平整,无起皱现象;当翻边宽度增大到30 mm时,工件最外缘有轻微波浪型褶皱,工件成形质量不好;当翻边宽度增大到40 mm时,工件出现了非常明显的起皱现象。通过模拟,大致可以确定径厚比为50的工件的旋压成形极限宽度约为30 mm,当旋压成形宽度大于或等于30 mm时将出现工件起皱现象,影响工件成形质量。

(a)b=25 mm (b)b=30 mm (c)b=40 mm图12 径厚比为50时工件的成形结果

将径厚比增大到70,翻边宽度为30 mm时得到的工件最外缘较为平整,无起皱现象;当翻边宽度增大到40 mm时,工件最外缘有轻微波浪形褶皱,工件成形质量不好。由此可以大致确定,径厚比为70的工件的旋压成形极限宽度约为40 mm,当旋压宽度大于或等于40 mm时将出现工件起皱现象。将径厚比增大至100,翻边宽度为50 mm时得到的工件最外缘仍很平整,无起皱现象;当翻边宽度增大到60 mm时,工件最外缘有轻微波浪形褶皱,工件成形质量不好。由此可以大致确定,径厚比为100的工件的旋压成形极限宽度约为60 mm。因此可以得出结论:增大径厚比可以提高旋压成形法兰的极限宽度。

3.2 起皱开始的时刻

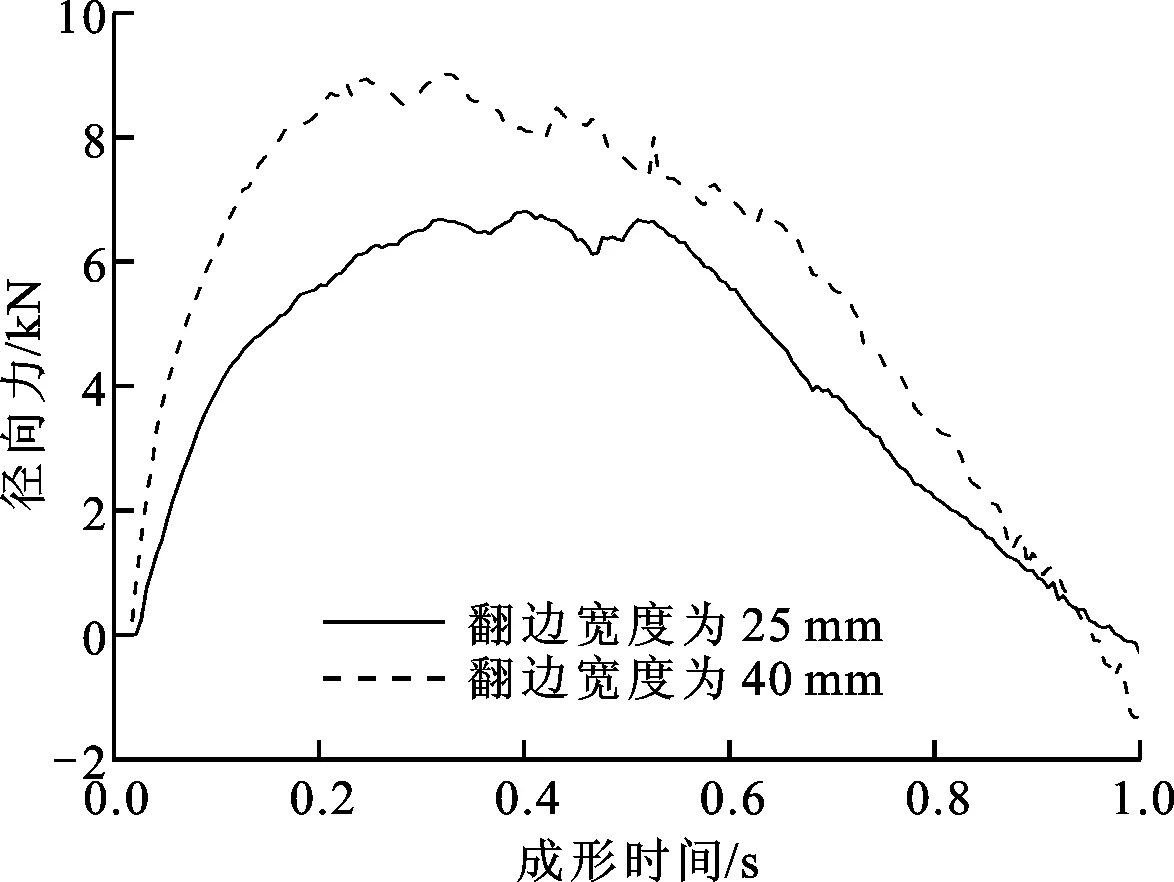
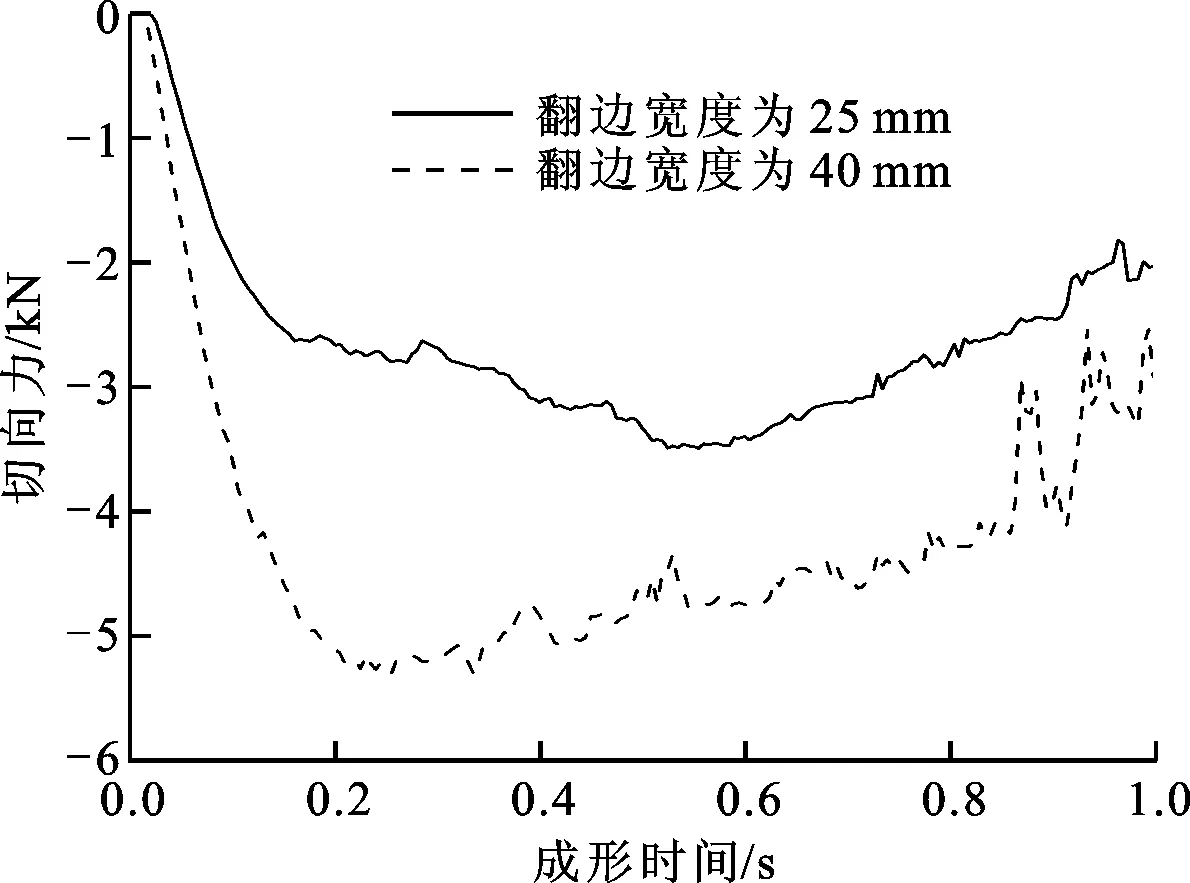
取坯料的壁厚为2 mm,内径为100 mm,径厚比为50,夹具转速取125.6 rad/s,旋辊进给率取0.079 rad/r,分析双金属复合管法兰翻边宽度分别为25和40 mm两种情况时旋压力的变化。双辊夹持旋压成形力分为径向力、切向力和轴向力3个分量,图13所示为2种翻边宽度条件下旋压力3个分量的变化曲线,可以看出不同翻边宽度工件的旋压力变化趋势相同,翻边宽度越大,旋压力的绝对值也越大。

(a)径向力

(b)切向力

(c)轴向力图13 2种翻边宽度条件下的旋压力曲线

由3.1节的分析可知:翻边宽度增大到一定值就会出现起皱缺陷;当坯料径厚比为50、翻边宽度为25 mm时工件无起皱,而当翻边宽度为40 mm时工件有起皱。观察图13中翻边宽度为40 mm时的旋压力变化曲线可以发现,径向力、切向力和轴向力曲线均在0.875 s时突然出现波动,尤其是切向力和轴向力曲线的波动更为明显。

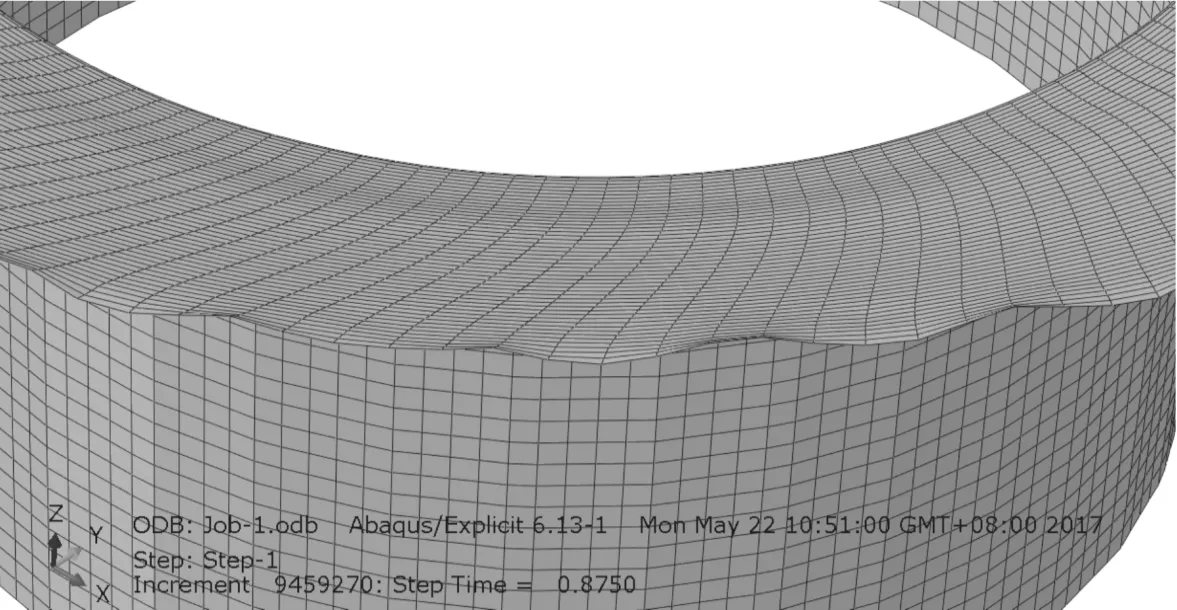
由图14可以看出,在成形0.875 s时工件法兰出现了明显的褶皱,而在之前的0.865 s时刻尚未出现起皱,由此可知是旋辊作用在变形区时发生了起皱,导致旋压力的突然波动。因此,旋压力曲线的突然波动可以用来确定起皱发生的时刻,而相关的结论在普旋成形起皱时刻判断中已有应用[14]。

(a)step time为0.875 s

(b)step time为0.865 s图14 翻边宽度为40 mm时工件的几何形状变化

3.3 切向应力分析

图15是径厚比为50、翻边宽度为20 mm的工件的双辊夹持旋压成形切向应力分布图,可以看到成形过程中旋辊接触部位受到较大的切向压应力,其余部位受到切向拉应力。随着成形的进行,在旋辊离开后此处的切向压应力会逐渐减小,甚至转变为较小的切向拉应力。

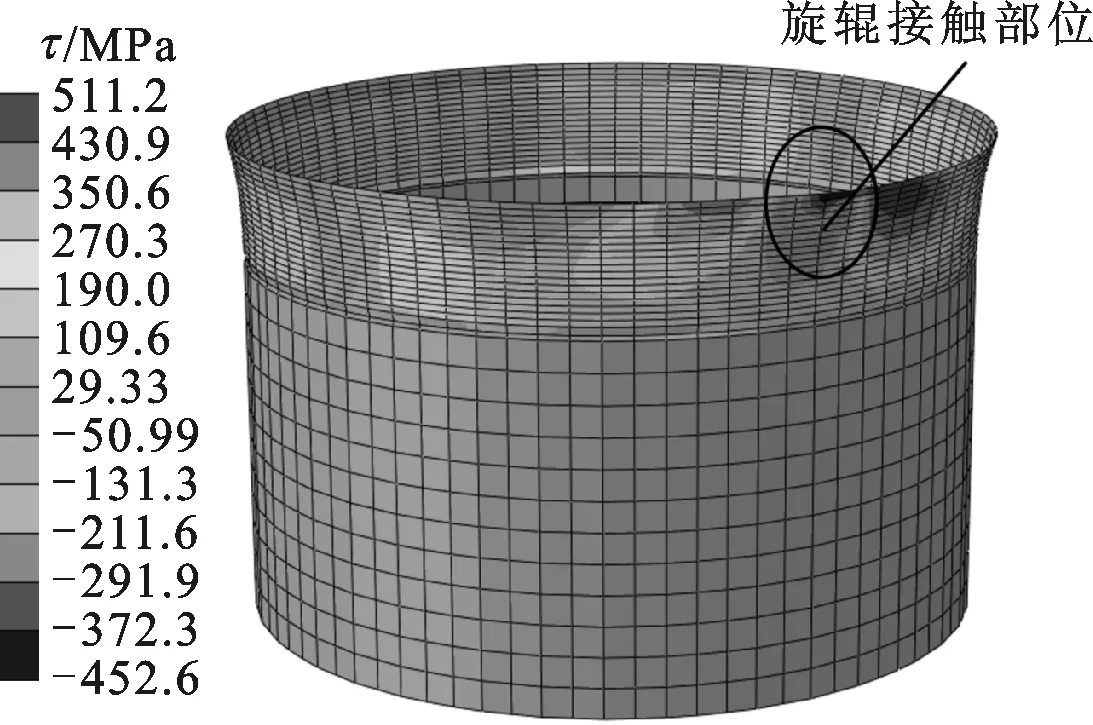
图15 旋压成形工件的切向应力分布图 (step time为0.19 s)

图16是翻边宽度分别为20和40 mm时的切向应力分布图,可以看到增加翻边宽度会使工件的变形程度加大,旋辊接触部位承受的切向压应力也增大。从图15和图16a可以看出,当step time为0.19 s时,翻边宽度为20 mm时的最大切向压应力为453 MPa,翻边宽度为40 mm时的最大切向压应力为590 MPa。当旋辊离开后,此处的切向压应力有所减小,但由于变形程度过大导致此处的切向残余应力最后仍是压应力,随着成形过程的进行,这一情况更加严重,如图16b和16c所示,从而导致了此处的起皱缺陷。

(c)step time为0.95 s图16 翻边宽度为40 mm时工件的切向应力分布图

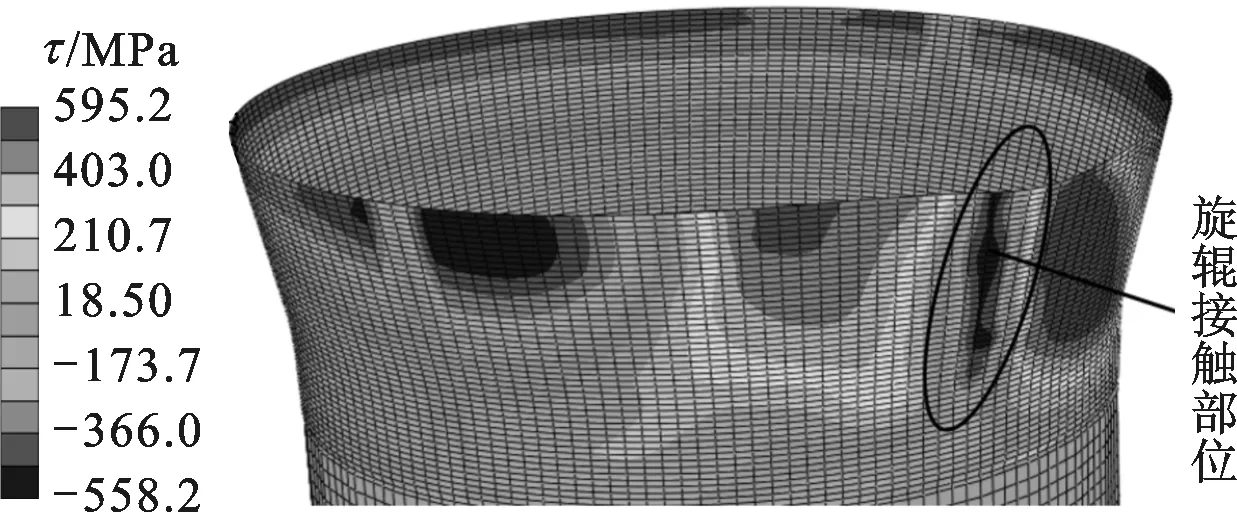
(a)径厚比为50

(b)径厚比为70图17 翻边宽度为30 mm时工件的切向应力分布图 (step time为0.19 s)

在同等条件下,增大径厚比可使双辊夹持旋压成形时工件的变形程度减小。图17是毛坯径厚比分别为50和70、翻边宽度均为30 mm情况下的工件切向应力分布图,可以看到,增大径厚比后旋辊接触部位所承受的切向压应力有所减小:径厚比为50时切向压应力为558 MPa,径厚比为70时切向压应力为532 MPa。在旋辊离开后其切向压应力也较小,相对不容易产生起皱。

图18是翻边宽度为30 mm的工件成形结束之后的切向应力分布图,可以看到,径厚比为50的工件的法兰外缘出现了轻微的起皱,而径厚比为70的工件的法兰成形良好,只有增大翻边宽度即增大变形量时才有可能产生起皱。随径厚比增大,工件成形的翻边宽度极限值也相应增大:当径厚比为50时,工件的翻边宽度极限值约为30 mm;当径厚比为70时,工件的翻边宽度极限值约为40 mm;当径厚比为100时,工件的翻边宽度极限值约为60 mm。

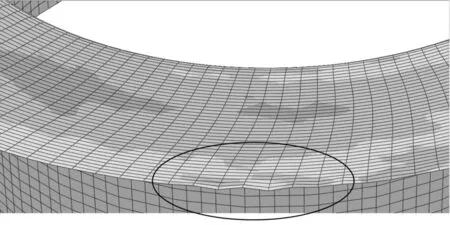
(a)径厚比为50

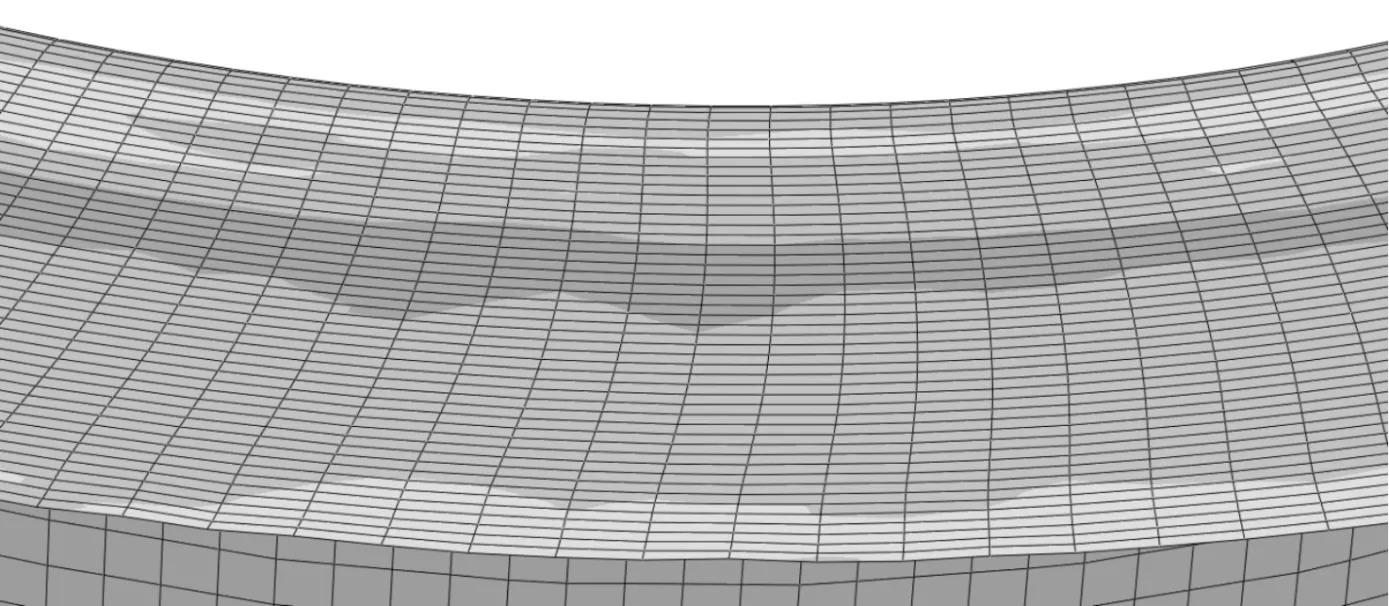
(b)径厚比为70图18 翻边宽度为30 mm时工件的切向应力分布图 (step time为1 s)

4 结 论

本文建立了Q235普通钢/304不锈钢双金属复合管法兰双辊夹持旋压成形的有限元仿真模型,对Q235普通钢/304不锈钢双金属复合管法兰双辊夹持旋压成形过程进行了有限元仿真模拟,分析了成形过程中易出现的起皱形式和影响因素,获得如下结论:

(1)随旋辊进给率增大所需要的成形转矩也变大,而最大壁厚差先减小后增大,然而旋辊进给率过大会出现不同程度的起皱现象。综合考虑,确定合适的旋辊进给率为0.079 rad/r。

(2)坯料径厚比越大,所需要的成形转矩就越小,而成形过程中旋辊接触部位存在切向压应力,随着变形程度的增大会导致外缘部分起皱,所以在一定的径厚比条件下可成形的法兰宽度存在极限值,大于极限值则会发生起皱现象。当坯料径厚比分别为50、70、100时,对应的极限翻边宽度分别为30、40和60 mm。

(3)可以根据旋压力曲线的突然波动来确定起皱发生的时刻。