超临界环己烷水平管内水动力学多值性研究

单亚飞,李天卉,杨竹强,张博,刘峰

(大连理工大学能源与动力学院,116024,大连)

随着新型高速飞行器机动性与多态化作战能力要求的不断提升,机载热载荷不断攀升。为了降低机载热载荷,以自身携带的燃料作为冷源的“再生主动冷却技术”成为了研究热点[1-3]。当燃料流经布置多通道形式的换热槽道时,虽然能吸收发动机表面的热载荷[4],但可能会出现流动不稳定的问题。这种静态不稳定性一方面会使壁温超温,出现传热恶化现象;另一方面还会引起机械振动,严重影响运行安全。

Ledinegg在1938年研究流体的静态不稳定性时发现:在特定条件下,通道内部的压降-流量(Δp-m)曲线存在一负斜率区;在这个负斜率区内,通道内的压降不是流量的单值函数,而是一个压降值对应多个流量值,这种水动力学多值性也称为水动力学特性,相应的这条曲线称为水动力学特性曲线[5]。Padki等分析认为,水动力学多值性是静态不稳定性发生的必要条件,研究水动力学多值性对于避免静态不稳定性的发生具有重要意义[6]。因此,学者们对水动力学特性展开了大量研究,不断发现其存在于两相换热或相变的流动过程中,并且认为气泡的生长以及气液间比体积的剧烈变化是促使其存在的主要原因。其中:Boure、Ruspini等相继对两相流体的静态不稳定性进行了综述[7-8];Chiapero在水平加热管中的水动力学实验中发现了减小工作压力、流体入口温度或轴向的载荷分布可以加剧流体的水动力多值性[9-10];Zhang等人采用数值计算方法分析了水平微通道中的静态不稳定性,结果表明,增加通道内压力或通道管内径(后文简称管径)以及减小通道数量或通道长度这4种方式均能使水平管换热系统更为稳定[11]。

对于超临界流体的水动力学特性的存在性,学者们仍未达成共识。Mahmoudi在水平矩形通道内开展了超临界CO2自然循环的热力-水力研究,实验发现:该物质具有水动力学多值性;增加通道内压力或减小流体初始焓值均有利于水平矩形通道的稳定[12]。Swapnalee等同样在超临界水的自然循环实验中发现了水动力学多值性,并且认为流体密度的剧烈变化是促使其存在的原因[13]。Chatoorgoon利用线性理论分析了超临界CO2和水的静态不稳定性,发现二者在向下流动的通道中静态不稳定性更易发生[14]。近期,Guo等通过实验证实了吸热型碳氢燃料中水动力学多值特性的存在,并且指出,拟沸腾和化学裂解是促使其存在的主要原因[15]。然而,也有部分学者认为水动力学多值性在超临界流体中并不存在。Yu等基于数值模型[16]、Liu等采用实验手段[17],对超临界流体的自然循环进行了研究,结果均未发现循环回路中存在水动力学多值特性。熊挺等采用自编程序SCIA对并联双通道内的超临界水流动不稳定的动态特性进行了研究,未发现水动力学特性曲线存在负斜率区,认为静态不稳定很难发生[18]。

在水动力学特性的研究过程中,流动不稳定起始点(onset of flow instability,OFI)的发生机理以及判定准则一直以来是学者们关注的重点。因为掌握了OFI的出发机制以及判定准则,将寻求到抑制或避免流动不稳定性发生的方法。Whittle和Yu等认为,单通道流体水动力学特性曲线的最低点可视为OFI[19-20]。同样的观点也被学者们在多通道内的流量分配过程中采用[21-22]。目前,针对OFI的研究集中在不同条件下的两相流体中,得到了一些预测OFI的经验公式。Duffey等运用分析模型研究了竖直管道内的静态不稳定性,结果表明,OFI与热流密度之间存在着线性关系[23]。一些学者研究认为,利用Saha-Zuber关联式预测得到的OFI对应的质量流量更为准确[24-28]。Whittle等研究了在近似大气压力下,长方形和圆形管道内过冷沸腾时的压力损失,研究认为,对于给定的管长径比,OFI发生在一固定值R=(Tout-Tin)/(Tsat-Tin)(Tout、Tsat和Tin分别表示出口温度、饱和温度和入口温度)处,该值为管路温升与过冷度的比值[19]。Dougherty等对管长径比为100～150的竖直管内的静态不稳定性进行了实验研究,发现基于实验数据计算的参数Qr=qπDl/(mCpf(Tsat-Tin))(q表示热流密度,D和l分别表示管外径和管长量,m表示入口质量流量,Cpf表示比热容)与Whittle提出的R一致[29]。基于参数Qr,一些学者通过研究得到了不同的用于预测OFI的经验公式[30-31]。考虑到管道结构参数对于静态不稳定性的影响,Babelli等运用数学模型预测了低压条件下流体向下流动时的OFI,获得了包含管长的模型公式[19]。Stelling等通过实验研究提出了包含管长和管径两种结构参数的经验关联式[20]。

基于上述文献的研究基础,本文的研究内容分别从以下3个方面进行:(1)验证超临界流体水动力学特性的存在,给出明确的水动力学特性曲线;(2)探究影响超临界流体水动力学多值性以及OFI的主要因素;(3)结合实验数据并采用归一化方法,给出OFI的预测关联式,为设计超临界流体换热结构提供参考依据。

1 实验系统及数据处理

1.1 实验系统

超临界环己烷流动换热实验系统主要由流体供给、流动管路、压力控制装置、参数测量系统和数据采集系统5部分组成。实验过程中,测试流体由恒流泵加压后以恒定体积流量流入实验管路,其质量流量由高精度质量流量计测量监控,同时,恒流泵和质量流量计入口分别装有过滤器,防止杂质污染;流入实验管路的流体经预热段加热至预设温度后,流体进入测试段;测量后的流体经冷凝器冷却后流出实验系统;整个过程中的系统工作压力由出口处的背压阀进行调节。实验系统简图如图1所示,实验测试参数如表1所示。

图1 超临界环己烷流动换热实验台系统

参数取值范围压力p/MPa4.0～5.5入口温度Tin/℃30～100热流密度q/kW·m-2158～450测试管长l/mm200～890测试管径d/mm1.0,2.0

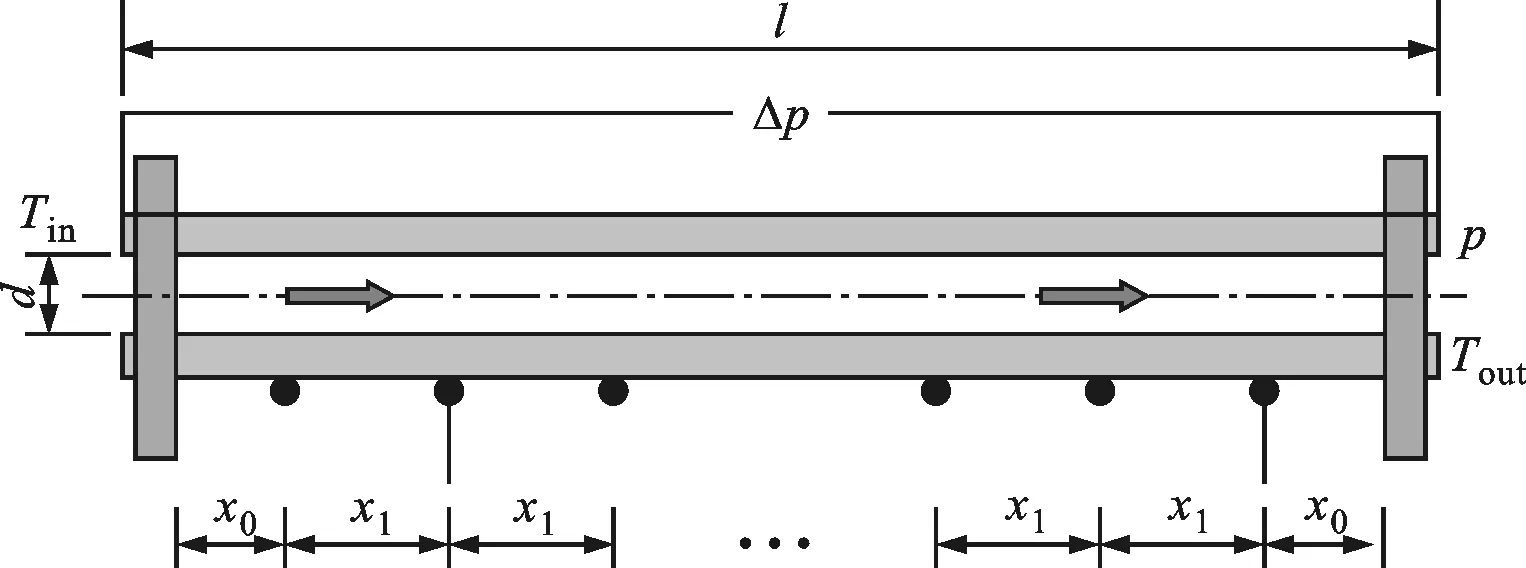
图2 测试段热电偶的分布

实验过程中,选取一定管长和管径的316不锈钢管为测试管路,维持系统的测试压力与流体入口温度在某一恒定工况。将质量流量由高到代调节,可得到相应测试段下的压降值,进而得到压降随质量流量的变化曲线,即为所研究的水动力学特性曲线。测试压降由安放在管路进出口处的压差传感器(Rosemount 3051CD4)测定,而管路表面的温度由焊接在管外壁的K型热电偶(Omega TJ36)测定。针对不同管长的测试管路,热电偶也采用了不同的分布方式,如图2和表2所示。为了减少测试管路的热量损失,测试管路还包裹玻璃棉作绝热处理。实验过程中严格控制测试管壁的温度不超过540 ℃,流体出口温度Tout不超过420 ℃,以确保测试工质不发生化学反应。

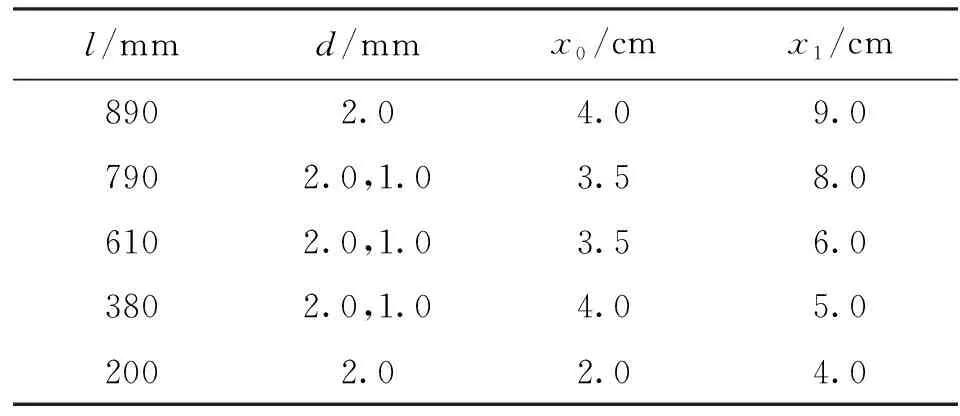
表2 热电偶分布位置

实验中采用纯度为摩尔分数99.5%的环己烷作为测试工质。

1.2 数据处理

测试段加热管外壁热流密度由下式获得

(1)

式中:I、U分别为交流电流与电压;Ql为加热管热损,计算为

Ql=-20.618+0.296T-7.650×10-4T2+

1.691×10-6T3-7.074×10-10T4

(2)

其中T为测试温度。测试温度范围内,Ql控制在总功率的6%以内。

流体焓值计算为

(3)

式中:x为热电偶的分布位置;hb,in为流体入口焓值;min为流体质量流量。

在NIST软件中查询管中流体焓值,可以得到对应的主流流体温度Tb。

管内壁温度Twi(x)通过管外壁温度Two(x)及管内热源qv(x)计算得出

(4)

式中:λ为管材导热系数;qv(x)的计算公式为

(5)

实验过程中系统参数的不确定度如表3所示。表3中,对于可以直接测量的物理量,如流体温度、体积流量、压力和压降,这些物理量的不确定度是由对应测量设备和采集卡的精度共同决定的。对于通过一些计算得到的物理量,如加热功率、热流密度、质量流量和内壁面温度,这些物理量的不确定度是由与之相关的一些基本测量量的不确定度累积而成的。假设物理量F由n个基本测量量Fi(i=1,2,3,…,n)合成,则其不确定度为

(6)

因此,热流密度q的不确定度计算为

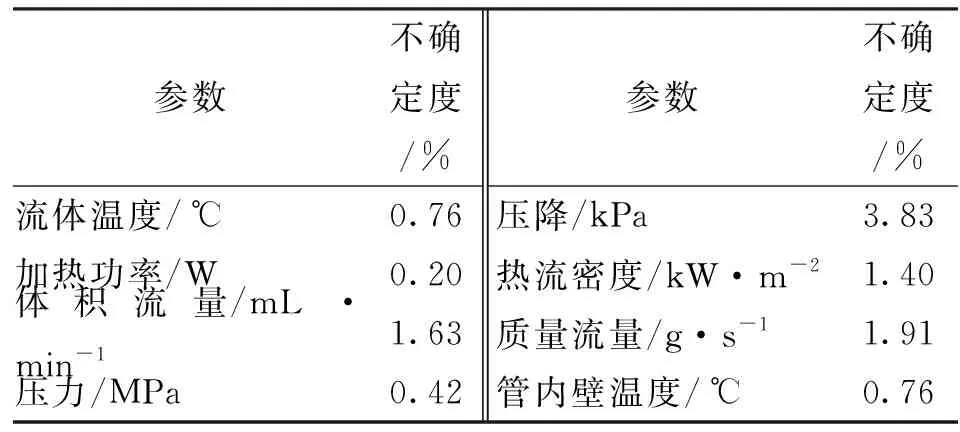
(7)

2 实验结果与讨论

2.1 水动力学多值性的存在

图3给出了在超临界压力(临界压力pcr=4.05 MPa)条件下,不同实验测试参数条件下获得的环己烷水动力学特性曲线,可以看出,水动力学特性曲线存在明显的负斜率区。因此,水动力学多值性在超临界流体中的存在性得到了证实。同时,多值性负斜率区间的斜率以及OFI随着压力p、入口温度Tin、热流密度q、管长l和管径d的不同而呈现出变化趋势。因此,需要针对不同的实验测试参数对超临界流体的水动力学多值性进行进一步详细的研究。

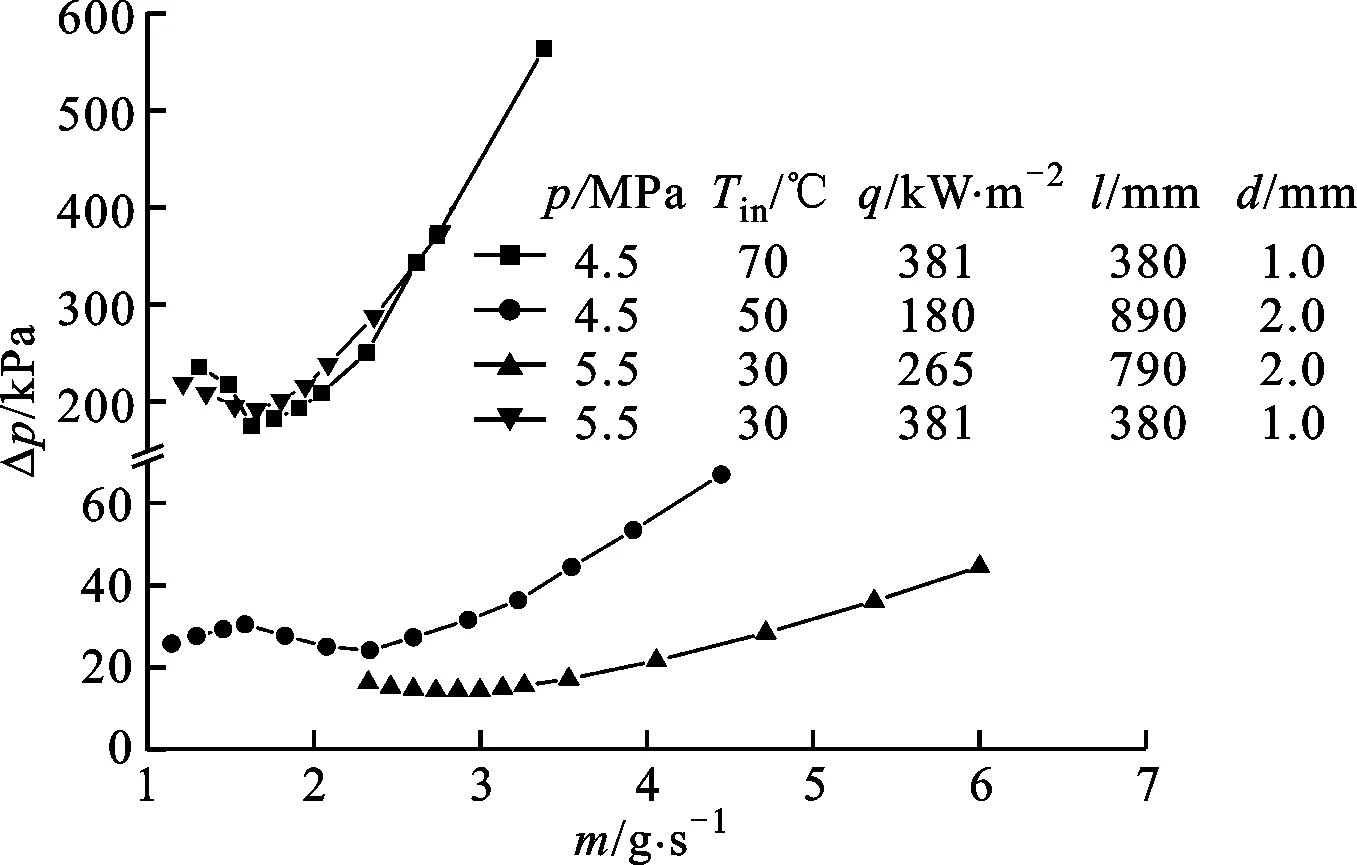
图3 超临界压力环己烷的水动力学特性曲线

2.2 压力对于水动力学多值性的影响

图4展示了水平圆管内水动力学特性曲线随着系统压力的变化规律,可以看出,随着系统压力的增大,水动力学特性曲线负斜率区域减小,即系统更加稳定。当系统压力低于临界压力(4.05 MPa)时,水动力学多值性明显,这是由相变点附近区域工质比体积的剧烈变化造成的[19]。当系统压力为4.5和5.5 MPa时,系统压力大于临界压力,同样存在负斜率区,这是因为与亚临界压力类似,超临界压力下工质在拟临界温度(见图4中所标注的直线288 ℃和303 ℃,这两个温度分别对应于4.5 MPa和5.5 MPa的拟临界温度)附近,密度急剧减小,比体积也受温度变化影响较大,只是程度相对要小一些。在超临界压力下,随着压力的增大,在拟临界温度附近,流体密度的变化趋势越来越平缓[13],同时,随着压力的增大,流体的拟临界温度增大,转变为超临界态点向后延迟,出现OFI对应的质量流量向低质量流量移动。因此,提高压力可以改善超临界压力下流体的水动力稳定性。

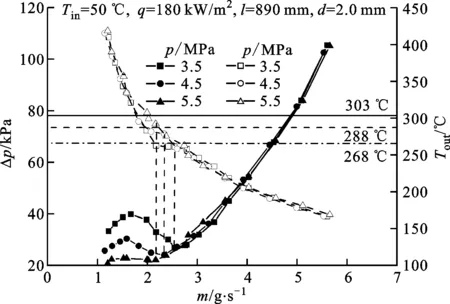
实心点:对应左侧压降坐标轴;空心点:对应右侧出口温度坐标轴图4 系统压力对于水动力学特性曲线的影响

2.3 入口温度对于水动力学多值性的影响

在超临界压力实验条件下,通过改变测试段入口温度,得到不同入口温度下通道内的水动力学特性曲线,如图5所示。

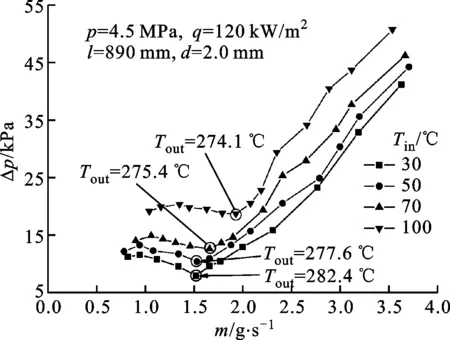
图5 入口温度对于水动力学特性曲线的影响

从图5中可以看出,随着入口温度的增加,负斜率区越来越平缓,水动力学多值性趋势减弱。因此,入口温度越高,越有利于提升系统的水动力学稳定性。同时,入口温度的增加使得单位流体到达负斜率区的起始点所需的热量变少,OFI对应的流量向高质量流量移动,且对应出口流体温度不断升高,接近拟临界温度点(Tpc=288 ℃)。

2.4 热流密度对于水动力学多值性的影响

超临界压力下热流密度对通道内水动力学特性曲线的影响如图6所示,可以看出,随着热流密度的增大,负斜率区越来越陡峭,水动力学多值性趋势增强。所以,降低热流密度有利于系统的水动力学稳定性。同时,热流密度的增大使得流体由更易由液态变为超临界态,OFI对应的质量流量向高质量流量移动。

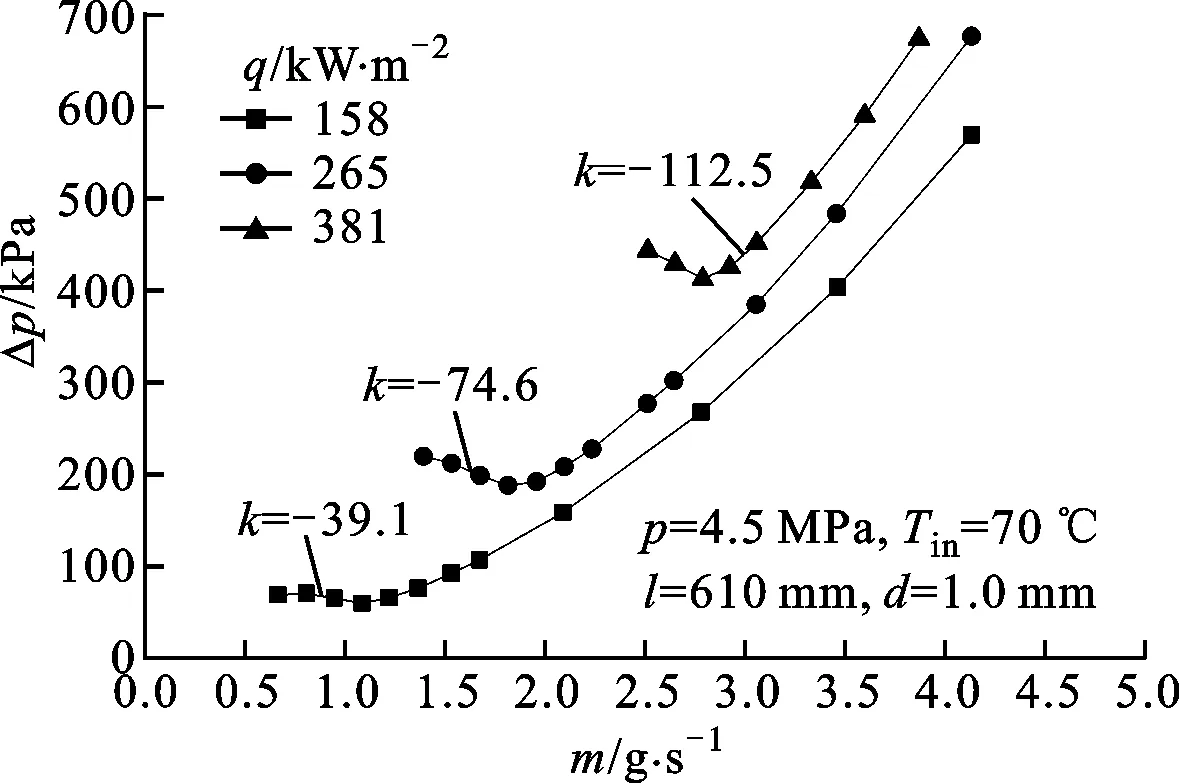
图6 热流密度对于水动力学特性曲线的影响

2.5 管长对于水动力学多值性的影响

图7展示了不同管长下通道内的水动力学特性曲线,可见在相同的实验参数条件下,随着管长的增加,负斜率区不断变大,也就意味着管长的增加会导致静态不稳定更易发生。这是因为在水动力学特性曲线负斜率区间,流体进入拟临界温度和超临界状态区间,此时流体的物性发生急剧的变化。在相同的热流密度条件下,管长的增加使得通道中工质由液态转变为超临界流体的过渡区间所占的比例增大,也就是管道内物性(尤其是密度)剧烈变化的区间长度增加。因此,管长越长,水动力学特性曲线的负斜率部分越陡峭。

图7 管长对于水动力学特性曲线的影响

2.6 管径对于水动力学多值性的影响

不同管径对于通道内流体的水动力学多值性的影响如图8所示,可以看出,在热流密度相同的情况下,管径越小,水动力学特性曲线的负斜率部分越陡峭,也就意味着水动力学稳定性越差。这是因为在相同工况条件下,管径的减小使得沿径向方向上的内壁面流体温度与主流温度的梯度增加,此时,近壁面流体温度显著高于拟临界温度,而主流温度则低于拟临界温度,如图9所示。此时径向的温度梯度增大导致了径向密度变化幅度和区间都增大,从而小管径通道内的水动力学特性曲线的负斜率部分变得陡峭。同时,小管径对应的测试段加载的热量变少。由于在相同流体入口温度条件下,流体达到拟临界温度附近所需的焓增基本相同,因此在小管径内OFI向低质量流量发展。

实心点:对应左侧压降坐标轴;空心点:对应右侧压降坐标轴图8 管径对于水动力学特性曲线的影响

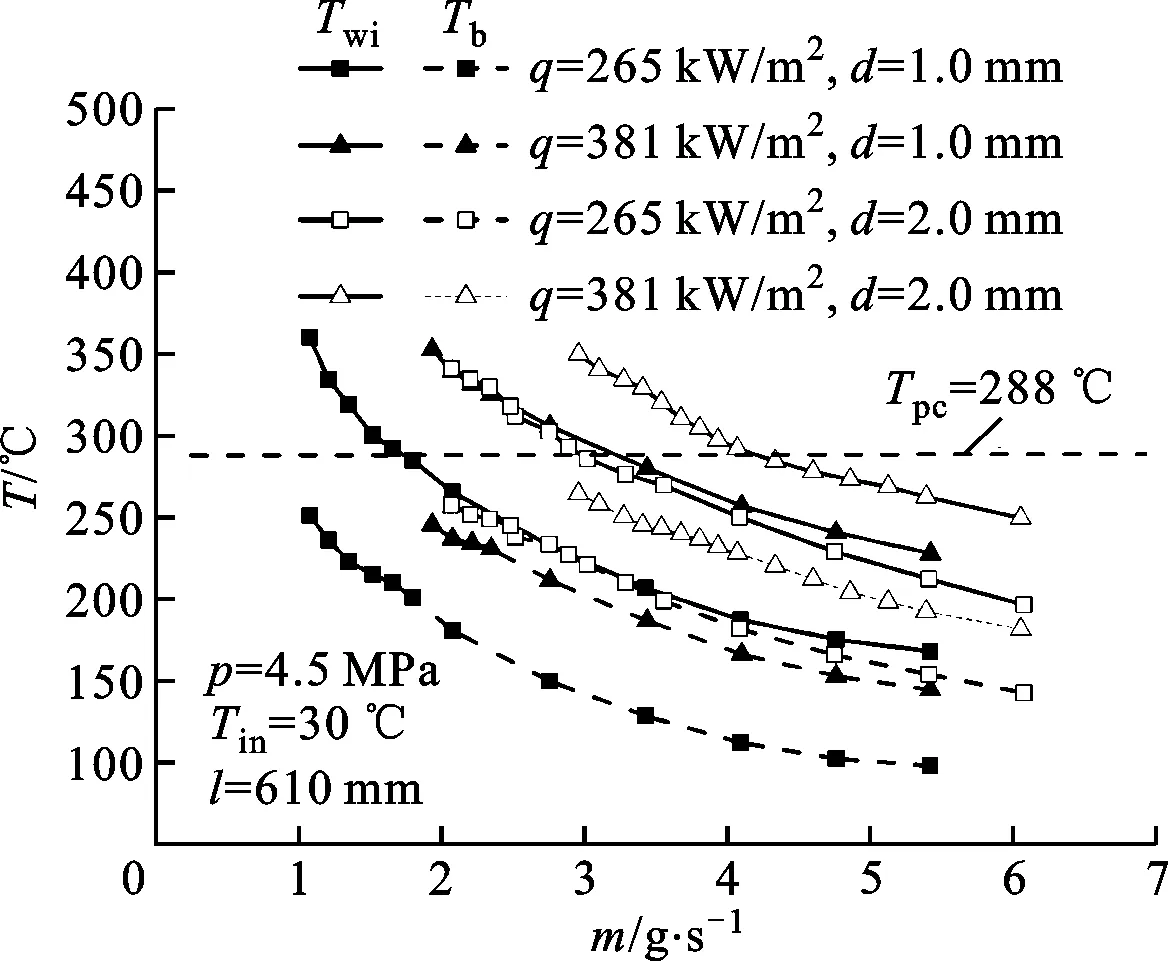
图9 x/l=0.85时不同管径下Twi和Tb 随质量流量的变化

2.7 OFI归一化准则分析

通过对实验数据的分析,发现影响水动力学特性曲线上OFI的主要参数有系统压力、入口温度、热流密度、管长和管径。首先,采用量纲分析得到一个预测OFI的经验关联式;然后,基于实验数据使用多元线性回归方法得到相应的系数值;最终,得到具体的归一化关联式。

基于上述影响因素进行量纲分析,描述OFI的方程可表示为

F(Q,m,l,d,Δhin,Δhout,ρ)=0

(8)

式中:Q表示加热量,代表热流密度的影响;m表示OFI出现时的质量流量;l和d分别表示管长和管内径;Δhin和Δhout表示入口和出口欠焓值,代表入口温度和压力的影响;ρ表示流体密度。

选择d、Δhin和ρ作为基本参量,通过π定理进行分析,得到4个量纲一参数如下

(9)

(10)

(11)

(12)

上述4个量纲一参数可简化为以下3个量纲一参数

(13)

(14)

(15)

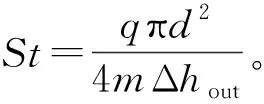
(16)

式中:C1、C2和C3是常数。基于实验数据,利用多元线性回归方法,得到水平管内预测OFI的归一化公式为

(17)

该公式应用范围为:100

3 结 论

本文通过实验研究了水平圆管内超临界环己烷在不同工况条件下的水动力学过程,得到以下结论。

(1)超临界压力下,流体水动力学特性曲线存在负斜率区,即水动力学多值特性存在。

(2)提高系统压力或入口温度、降低热流密度、减小加热管长、增加加热管径,均有利于提升系统水动力学稳定性。

(3)降低系统压力、提高入口温度、增大热流密度,会使得OFI对应的质量流量向高质量流量方向移动,相反,减小管长和管径将促使OFI向低质量流量方向移动。

(4)通过归一化方法,获得了适用于超临界流体OFI的预测公式。