一种L形大推力板结构直线超声电机

张百亮,姚志远,刘振,李晓牛

(南京航空航天大学机械结构力学及控制国家重点实验室,210016,南京)

直线超声电机是一种利用压电陶瓷逆压电效应和弹性体超声振动的新型作动器,通过给压电陶瓷施加交流激励电压,激发定子弹性体中特定的振动模态,从而在驱动足处形成椭圆或倾斜直线运动轨迹,进一步通过摩擦耦合推动动子作直线运动。直线超声电机具有结构简单、响应快、断电自锁、功率密度大和定位精度高等优点,已被广泛用于航空航天、武器装备和精密仪器等领域[1-2]。

直线超声电机按照波动方式可分为行波型和驻波型。最早的行波型直线超声电机是Sashida等于1982年提出的直梁式和环梁式,它利用两个兰杰文振子在梁中产生行波来驱动动子,由于工作时必须使梁的整体产生振动,因而这类电机功耗大,输出效率低[3]。1998年,Kurosawa等利用两个相互垂直的兰杰文振子设计了一种V形驻波型直线超声电机,它利用频率接近的对称和反对称模态在驱动足处形成椭圆运动,驱动动子运动,最大输出力为51 N,推重比为17[4]。这种V形直线超声电机具有高速、大推力的特点,成为了直线超声电机设计的典型结构形式,受到了国内外学者的关注[5-6]。2008年,姚志远等人对V形定子采用了连续变截面设计,进一步提高了电机输出效率,样机最大推力为21.4 N,推重比为25[7]。2014年,刘振等人提出了一种一端铰支的夹持方式,即定子一端铰支固定,另一端通过弹簧施加预压力[8]。这种夹持方式省去了传统超声电机中用于固定定子和调节预压力的夹持框或类似的装置,简化了电机结构并提高了电机的稳定性和输出力。2017年,Jian等人将这种夹持方式应用于V形电机,设计的样机定子尺寸为91 mm×50 mm×8 mm,输出力提高至43 N,推重比达到46.7,并在绝对重力仪中的驱动自由落体装置里得到了应用[9]。之后,Li等人对V形定子的两振子耦合角度(夹角)进行了研究,仿真和实验表明两振子相互垂直布置时电机输出性能最佳[6,10]。

尽管V形电机在一定体积范围内的输出力得到了提高,但仍不能满足要求更大推力或更小安装空间的作动场合。另外,对于模态耦合型超声电机,定子尺寸的改变将会破坏两相工作模态频率的一致性,使得电机设计的灵活性大大降低,难以满足不同应用的需求。采用单模态驱动是解决上述问题的一种方法,其中,板结构单模态电机因具有扁平化结构、空间利用率高和易微型化等特点,特别适用于扁平、紧凑型的作动空间,因而受到了广泛关注[11-12]。2017年,Liu等提出了一种单模态超声电机,它利用矩形板结构的一阶弯振和一阶纵振模态,通过切换两相模态实现电机的双向运动,实验表明,电机在弯振模态下具有较好的机械输出特性,最大推力为65 N[13]。

本文结合V形电机和矩形板结构电机的特点,利用两个相互垂直的矩形板振子构造了一种L形定子,其中一个振子与导轨平行安装,使电机结构更加紧凑,提高了空间利用率。在工作方式上,电机采用单模态驱动,利用两个矩形板振子弯曲振动形成的对称和反对称模态驱动导轨,通过模态切换实现了电机的双向运动。

1 电机结构及工作原理

图1为L形板结构直线超声电机的结构。该电机由定子、直线导轨、预压力施加装置和底座组成。定子呈L形,由两个相互垂直的矩形板振子组成,如图2所示。前端盖的两个端面均加工有螺纹孔,通过螺栓将后端盖、夹持、压电陶瓷片和电极片紧固为一体,构成一个夹心式压电振子。两振子关于前端盖的正对角线轴对称,驱动足位于前端盖顶点。这种夹心式压电振子采用压电陶瓷机电耦合系数较高的d33模式工作,可有效地提高电机的能量转换效率和输出性能[13]。

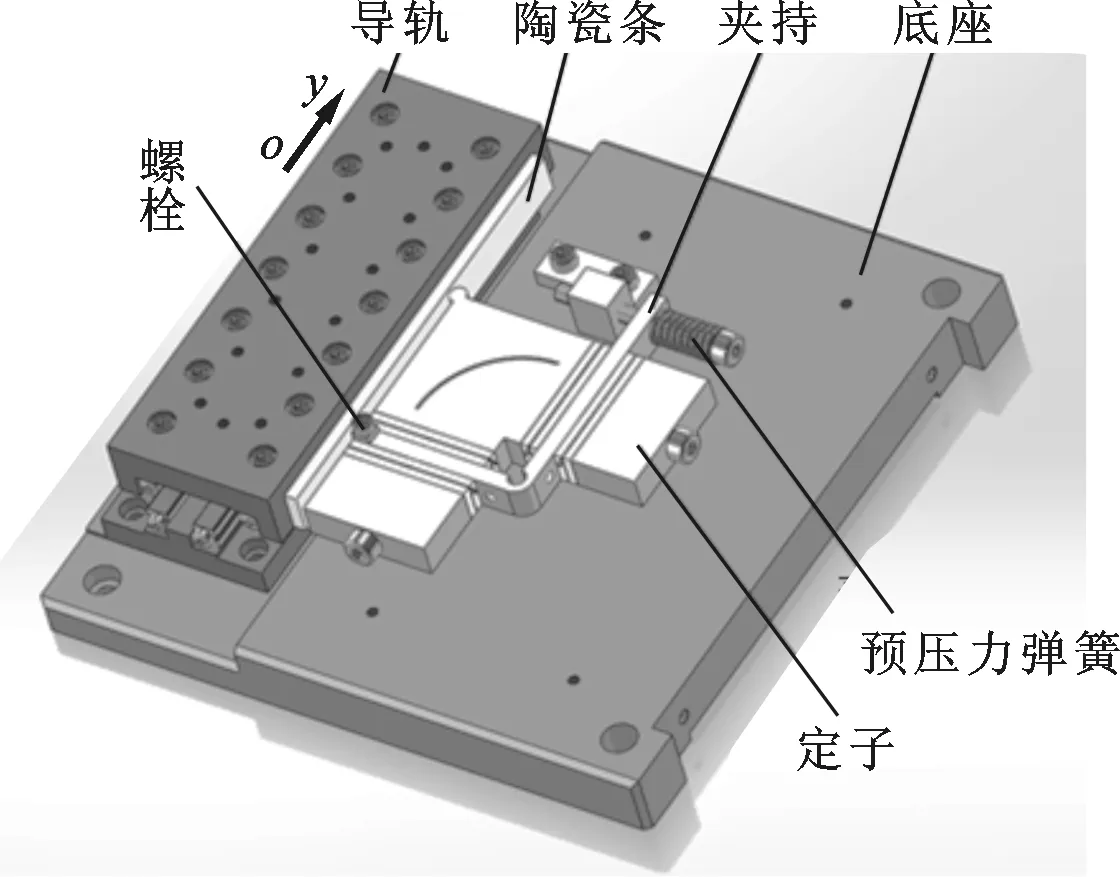
图1 L形板结构直线超声电机

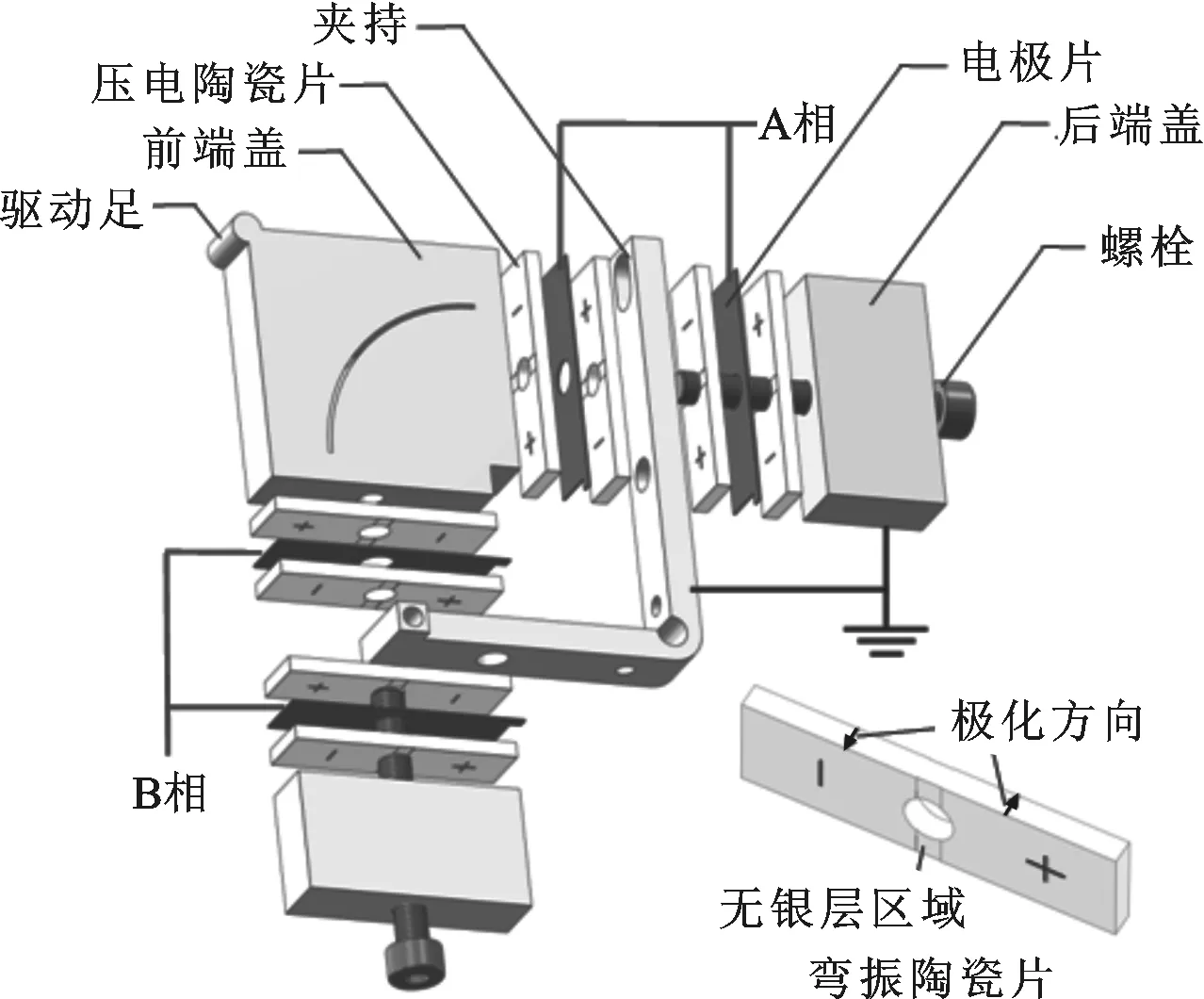
图2 定子结构

电机装配时,定子的一个振子与导轨平行安装,使电机结构更加紧凑,提高了空间利用率。定子夹持一端通过螺栓铰支在底座上,另一端通过预压力弹簧使驱动足紧压在陶瓷条上,为二者接触界面提供法向预压力。这种一端铰支的夹持方式具有理论上无穷大的切向(沿导轨运动方向)刚度且限制了定子的平动自由度,有利于提高电机的推力和输出性能的稳定性[9]。

每个矩形振子关于夹持对称地配置4片弯振陶瓷片,位于同一振子上的两电极片用导线连接,构成了定子的A、B相;前后端盖和夹持做接地处理。图3为自由-自由边界条件下,两振子发生同相或反相一阶弯曲振动时形成的对称和反对称模态,压电陶瓷片和夹持安置在模态波峰或波谷位置附近,以有效地激发矩形板的弯曲振动和降低夹持对振动模态的影响[14]。图3显示,对称模态在前端盖存在较大区域的振动节点,从而严重限制了驱动足处的振幅,不利于定子振动能量的输出。为此,在前端盖开设了一道圆弧通槽,用于释放前端盖的模态应力,消除驱动足附近的振动节点,最终以达到增加驱动足处振幅的目的,定子开槽后的振动模态为图4。

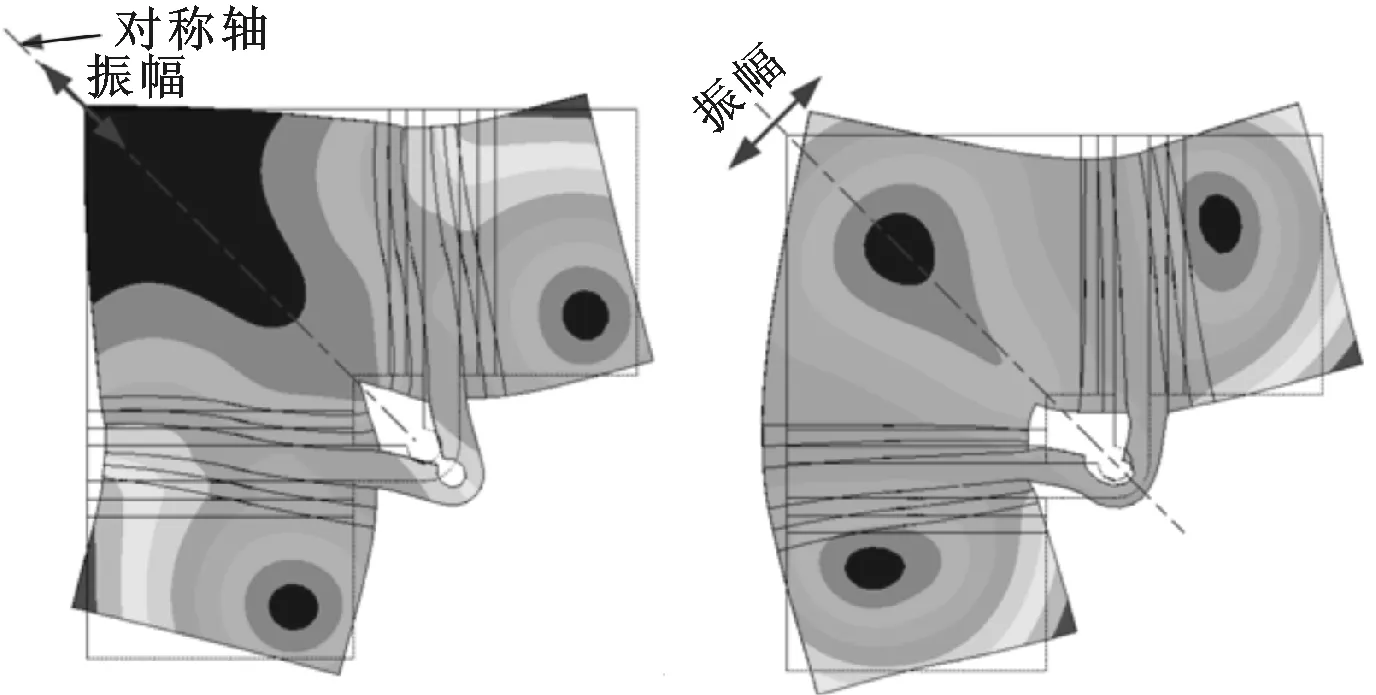
(a)对称模态 (b)反对称模态图3 定子的振动模态

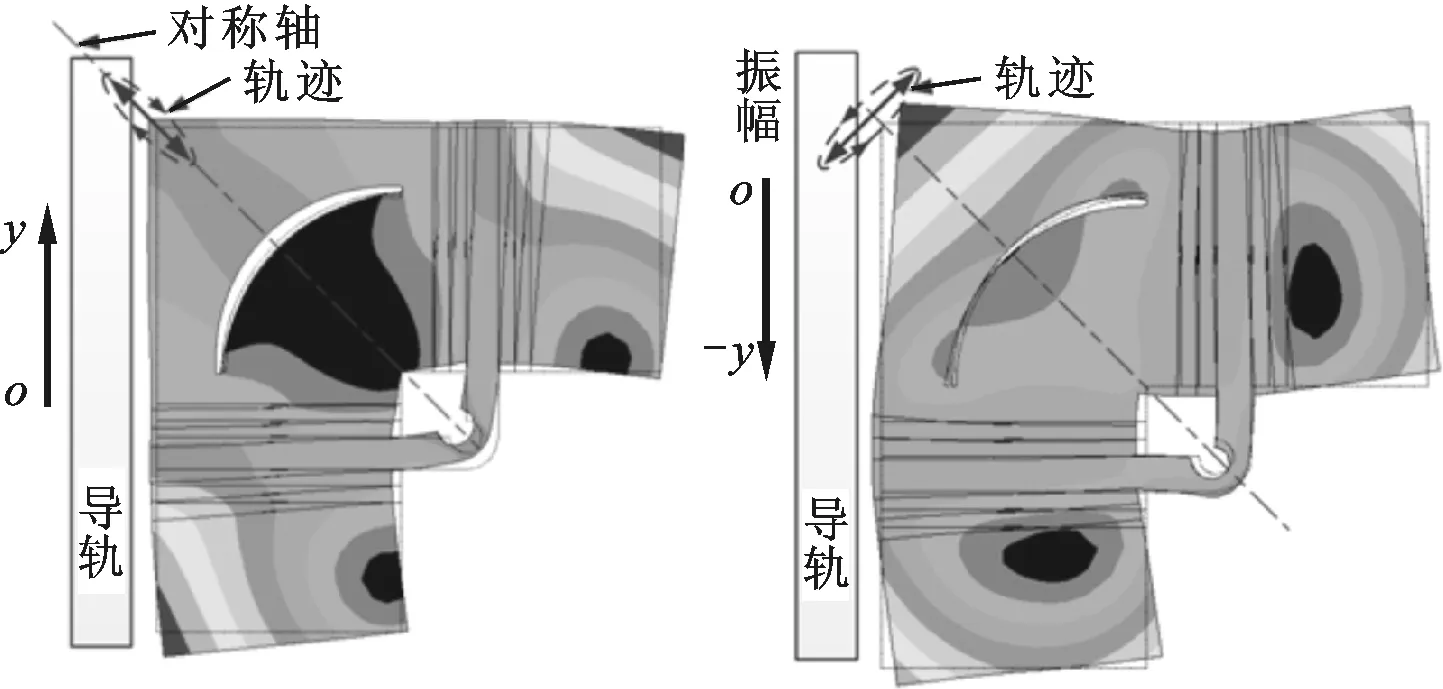
(a)对称模态 (b)反对称模态图4 开槽定子的振动模态

选择定子开槽后的对称和反对称模态作为工作模态。当对定子A、B两相施加相位差为0的正弦激励时,两振子做同相弯曲振动,定子的对称模态被激发,此时驱动足沿定子对称轴的方向做往复直线运动。驱动足在预压力的作用下与导轨接触,考虑到驱动足处的弹性变形,驱动足上接触点的运动轨迹将变成一个倾斜的扁平椭圆[12]。接触点的椭圆运动单向地间歇驱动导轨,进而推动导轨沿y方向做直线运动。同理,当对A、B两相施加相位差为π的正弦激励时,定子的反对称模态被激发,此时驱动足沿垂直于定子对称轴的方向做往复直线运动并在接触状态下产生反向的椭圆运动,从而推动导轨沿-y方向运动。

2 定子结构设计

2.1 开槽尺寸设计

采用单模态驱动的超声电机由于不需要考虑模态频率一致性的要求,因而具有尺寸设计灵活的优点,可根据应用场合的需要进行设计。本文选用的定子结构参数如图5所示,单个振子的特征尺寸为62 mm×30 mm×8 mm。前端盖开设的圆弧通槽宽为0.5 mm,半径为R。驱动足部分仅通过前端盖颈部线段AB和线段A′B′与定子剩余部位连接,考虑连接强度和避开内螺纹等因素,将R限制在8～12 mm或18～22 mm范围内。

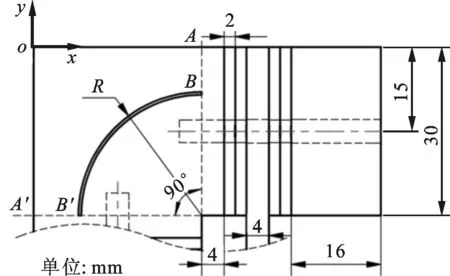
图5 定子结构参数

借助ANSYS的APDL语言建立定子有限元模型,对压电陶瓷和金属弹性体分别采用SOLID226和SOLID186单元进行网格划分,在自由-自由边界条件下,给定子施加峰峰值为200 V的激励电压进行谐响应分析,计算得到在对称和反对称模态下驱动足沿y方向的振幅(分别记为A1,y和A2,y)随R的变化规律,如图6所示。

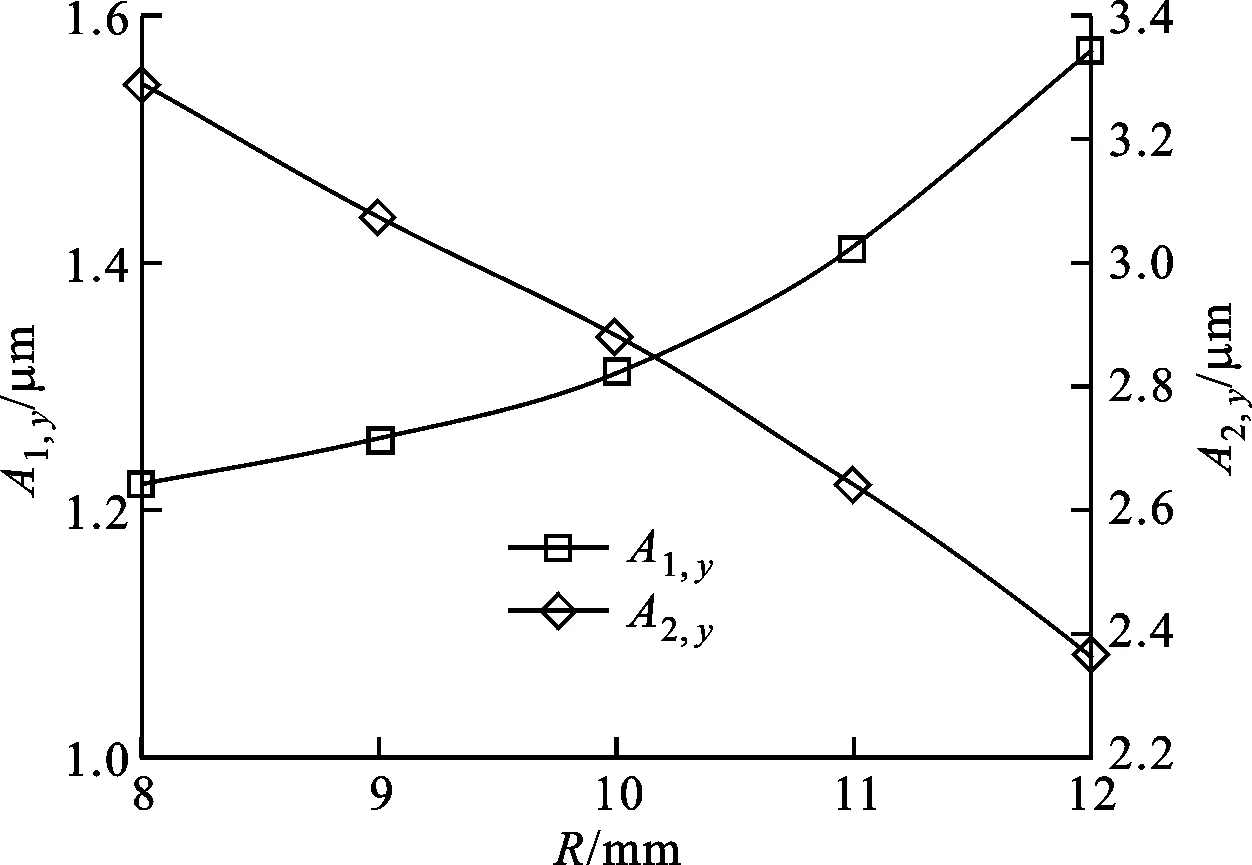
(a)8 mm≤R≤12 mm

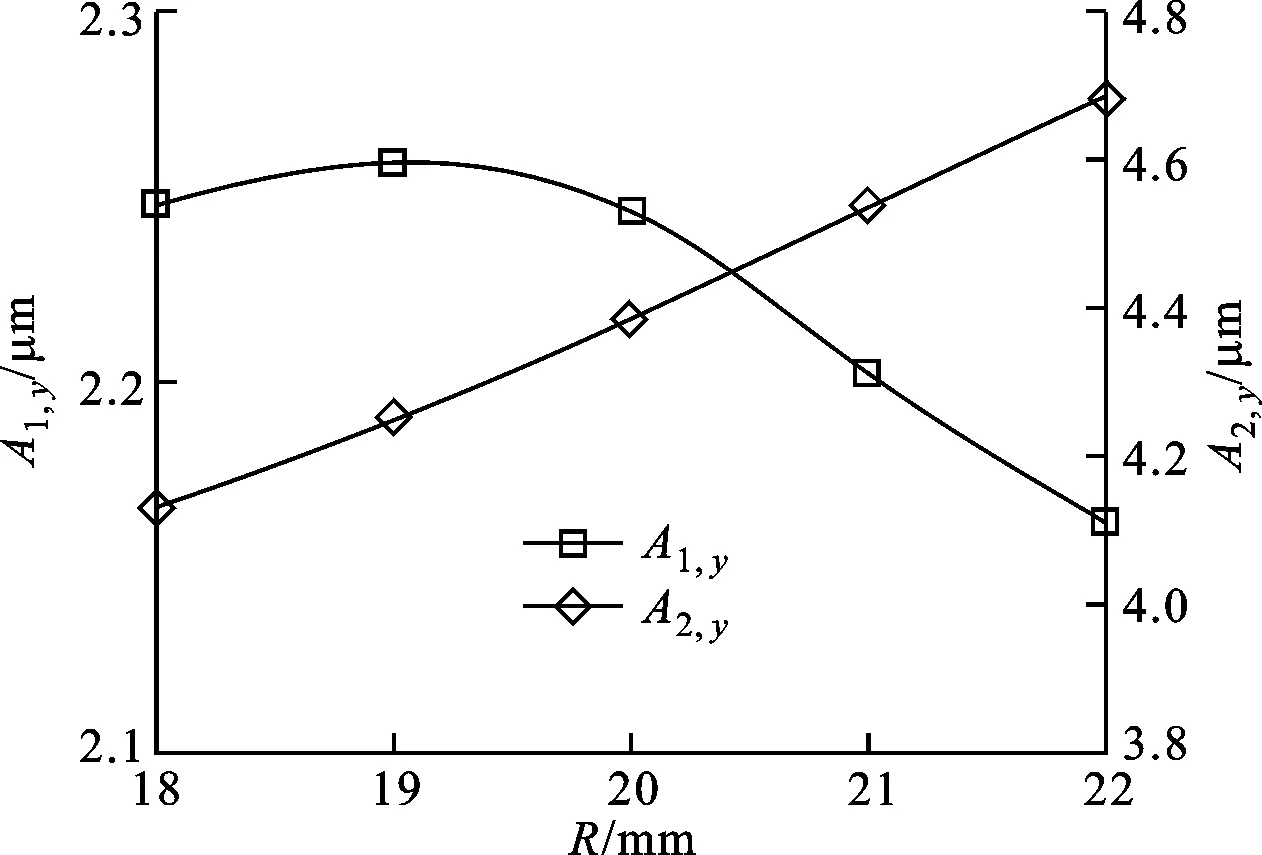
(b)18 mm≤R≤22 mm图6 R对驱动足振幅的影响

从图6可以看出,当18 mm≤R≤22 mm时,更有利于提高驱动足的振幅,此时A1,y的变化不大,而A2,y随着R的增大而增大。因此,参数R确定为22 mm。上述参数下的定子模态如图4所示,对称和反对称模态的固有频率分别为29.4 kHz和27.3 kHz,驱动足振幅分别为2.16 μm和4.68 μm。

2.2 振子螺栓紧固形式设计

夹心结构的压电振子通常采用预紧螺栓将各部件拧紧在一起,如图7a所示。对压电陶瓷施加一定的预应力,保证压电陶瓷工作时始终处于压应力状态,从而使其可采用高幅电压激励,提高电机的输出能力[15]。如果预应力太小,陶瓷工作过程产生的伸张应力可能会大于预应力,导致不同材料间的界面损耗增加,机械阻抗增加,机电转换效率下降。振子所采用的螺栓紧固形式(包括预紧螺栓的数量和位置)会直接影响压电陶瓷中预应力的大小和分布,因此有必要对其进行合理设计以提高紧固效果。

将图7a中振子采用的螺栓紧固方式描述为一组机械弹簧模型,预紧螺栓和振子分别等效为刚度为k0和ks的线性弹簧。若用n根相同的螺栓紧固振子,则螺栓的总刚度为kb=nk0=nEAb/Lb,式中E、Ab、Lb分别为螺栓的弹性模量、横截面积和长度。kb和ks如图7b所示。

(a)振子基本结构 (b)自由状态下力学模型

振子装配时,为防止拧紧预紧螺栓时振子的转动以及各部件间胶粘层的破坏,通常用夹具预先将振子夹紧,之后通过扭矩扳手拧紧螺栓,施加装配预紧力,最后松开夹具,完成装配。上述装配过程可以通过图7b～7e来进行说明:图7b为初始状态,螺栓处于自由状态;图7c为夹具夹紧振子状态,压电陶瓷被压缩;图7d为施加螺栓预紧力状态,螺栓被拉伸;图7e为夹具松开状态,振子发生压缩回弹,螺栓被进一步拉伸。

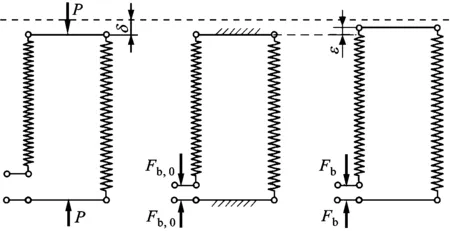
(c)夹具夹紧 (d)施加螺栓预紧力 (e)夹具松开图7 振子结构及螺栓紧固力学模型

在上述过程中,振子在夹具施加的夹紧力P的作用下,产生的压缩量为

(1)

扭矩扳手对每根螺栓施加的预紧扭矩均为T0,忽略螺栓拧紧顺序对装配体的影响,则螺栓紧固件受到的总预紧力Fb,0与预紧扭矩T0之间的关系为

nT0=KdFb,0

(2)

式中:K为扭矩系数;d为螺纹公称直径。

松开夹具后,振子将产生一个压缩回弹量ε,螺栓被进一步拉伸,螺栓中的总预紧力增加至Fb。根据变形协调条件,有

(3)

根据式(1)～(3),压电陶瓷中的预应力为

(4)

式中:λ=ks/k0;A为振子的横截面积。

从式(4)可以看出,增大夹紧力P或预紧扭矩T0可提高压电陶瓷的预应力。但是,夹紧力过大会压碎压电陶瓷,其大小一般根据实验确定。由于螺栓在断裂前的屈服阶段就已经产生了预紧力的损失,因此螺栓上能够施加的扭矩大小由螺栓材料的屈服强度σy决定,并满足以下关系

T0/(Kd)=Abσy/S

(5)

式中S为安全系数。

将式(5)代入式(4)得

(6)

从式(6)可以看出,适当地增大螺栓横截面积或振子横截面积的比值(Ab/A)可以提高压电陶瓷的预应力。但是,螺栓横截面积过大会使陶瓷的有效工作面积减少,导致振子的机电耦合系数损失严重。因此,基于实际考虑,预紧螺栓的横截面尺寸一般为振子横向尺寸的1/4～1/3[16]。由于板结构振子为扁平结构,其横向尺寸大、厚度小的特点限制了使用的预紧螺栓的直径规格,仅使用1根预紧螺栓难以达到上述紧固要求。式(4)表明,增加预紧螺栓的数量也可以提高压电陶瓷中的预应力。因此,可通过使用多根预紧螺栓达到增大螺栓紧固作用面积的目的。本文的振子厚度为8 mm,横向尺寸为30 mm。使用2根M4螺栓紧固时,预紧螺栓的横截面尺寸是振子横向尺寸的4/15,可见选用2根预紧螺栓是合适的。此时,压电陶瓷中的预应力σ2与单根螺栓紧固时的预应力σ1的比值为

(7)

在设计振子紧固方式时,压电陶瓷中预应力的均匀性也是一个非常重要的因素。均匀的预应力可保证振子获得较高的机械品质因数和较低的机械损耗[16-17]。目前,板结构振子多采用常规的兰杰文振子紧固方式[12-13],即在振子横截面中部位置使用单根螺栓进行紧固,如图8a所示。但是,板结构振子横向尺寸大,而且特别是当后端盖的纵向尺寸较小时,极易造成端盖和压电陶瓷接触面之间的预应力分布不均匀。因此,将2根螺栓安排在振子横截面中部两侧的中心位置,如图8b所示,以保证预应力的均匀分布。

(a)中部单螺栓紧固 (b)两侧双螺栓紧固图8 螺栓紧固横截面视图

此外,根据式(4)可计算出,采用双螺栓紧固和采用单螺栓施加2倍预紧扭矩时,二者压电陶瓷的预应力比值为

(8)

由于在装配过程中夹具施加的夹紧力能够保证夹具始终处于夹紧状态,因此P-2T0/(Kd)>0,故σ2>σ2T,由此可见采用2根螺栓紧固要好于对单根螺栓施加2倍预紧扭矩的效果。一方面,预应力得到提高,进而压电陶瓷的有效接触面积增加,弹性波的作用范围增大;另一方面,采用单螺栓紧固时由于施加的预紧扭矩过大而造成的螺栓失效问题得到避免,具有较高的安全系数。此外,相比采用1根中部螺栓紧固,在横截面中部两侧采用双螺栓紧固能获得分布较为均匀的预应力,振子弯曲振动时各部件结合面两端位置预应力的损失减少,接触面的分离和滑动得到抑制,从而界面损耗降低,有利于振动能量在振子中的传递,提高电机的机械输出性能。

3 实验研究

为验证定子设计的可行性,制作了2种实验样机,图9为样机照片,电机装配时对每根螺栓均施加4.5 N·m的预紧扭矩。采用多普勒激光测振仪(PSV-300F-B,德国Polytec公司)对样机进行扫频实验,测定结果见图10。模态测试过程中,选择前端盖上靠近驱动足的1个侧端面作为测试面,并给定子A、B两相施加峰峰值为80 V、相位差为0或π的激励电压。

图9 样机照片

从图10可以看出,各样机的2条频响特性曲线分别有一较大峰值,对应的频率即为对称模态共振频率(f1)和反对称模态共振频率(f2)。样机的两相工作模态实际频率与有限元仿真结果略有差异,主要是因为ANSYS在仿真过程中对有限元模型进行了简化,且未考虑预紧螺栓的预紧力以及加工和装配误差等因素。

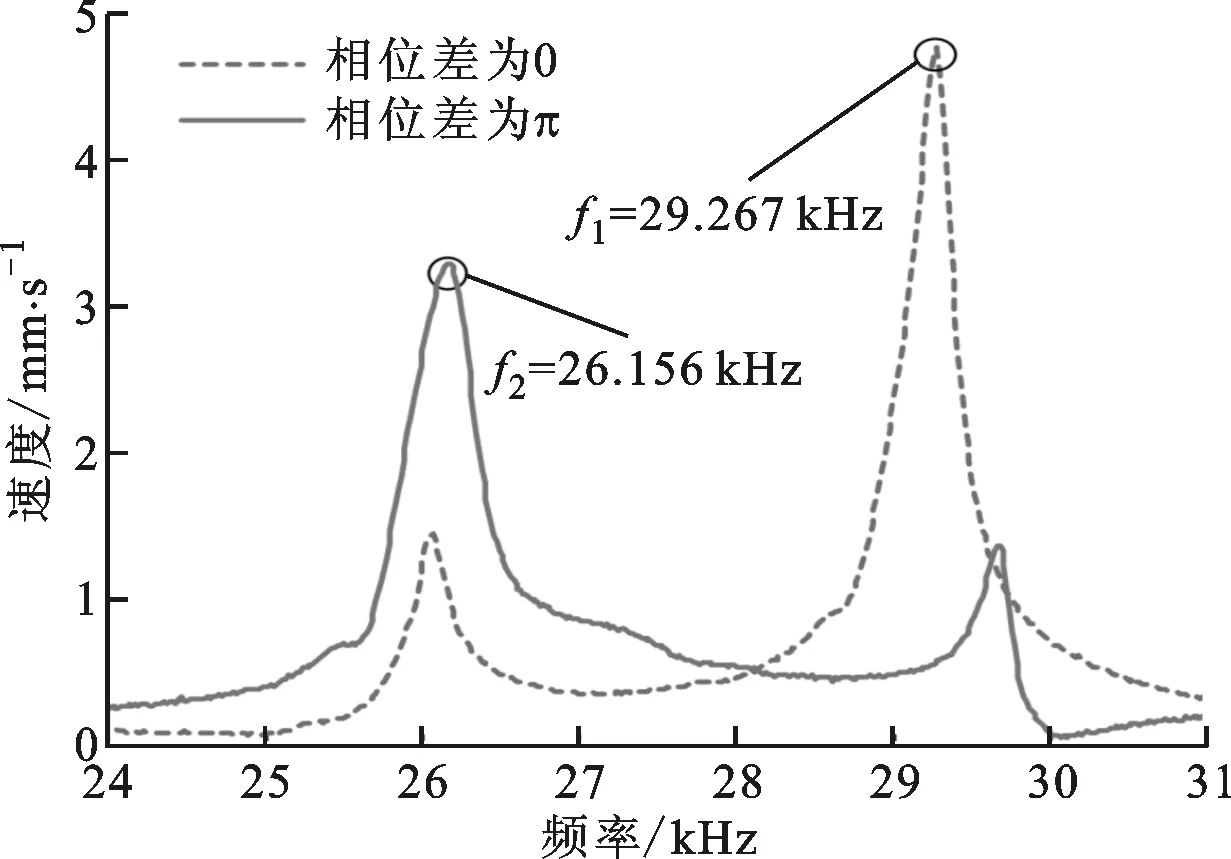
(a)单螺栓样机

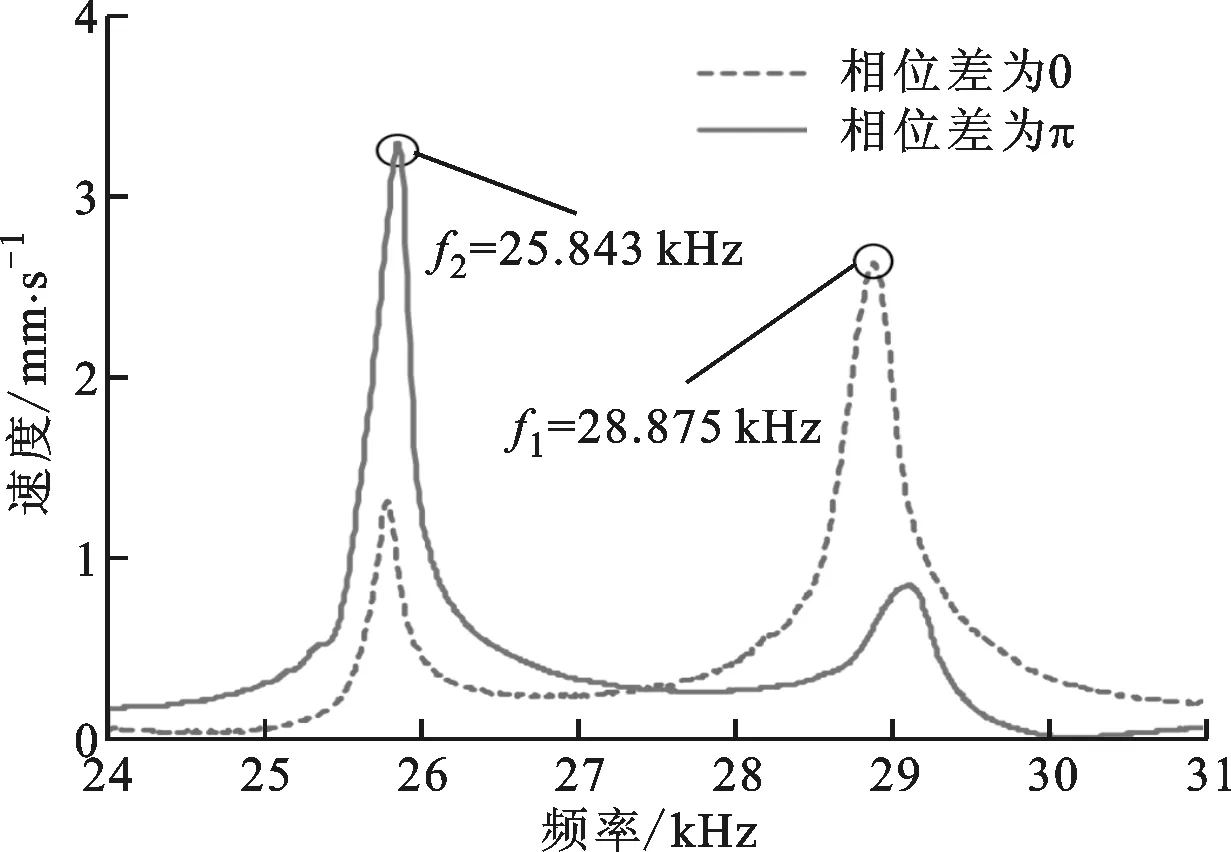
(b)双螺栓样机图10 定子频响特性曲线

对电机的机械输出特性进行测试,设计的实验平台如图11所示。由信号发生器产生的两相相位差为0或π的正弦信号经过功率放大器放大后,施加到定子的A相和B相以驱动电机。采用在直线导轨上吊砝码的方式为电机提供负载,导轨运动速度通过高速激光位移传感器测得。

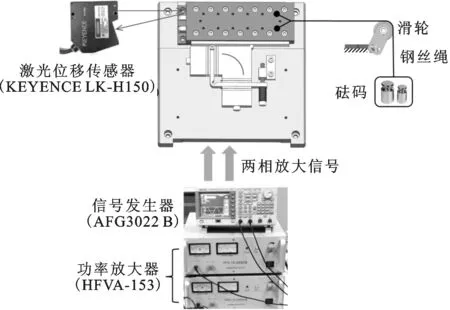
图11 电机的机械输出特性实验平台

图12为在预压力为100 N、激励电压峰峰值为500 V时,样机的空载速度频率特性曲线,可以看出:在工作频率范围内,电机的空载速度随着频率的升高先增大后减小;单螺栓样机的对称和反对称模态分别在频率27和24 kHz附近有最大空载速度384和293 mm/s;双螺栓样机的对称和反对称模态分别在频率27.4和25 kHz附近有最大空载速度405和435 mm/s。实验结果说明,采用双螺栓紧固方式可提高电机的输出速度。

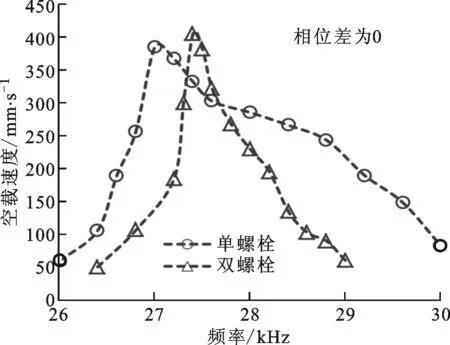
(a)对称模态

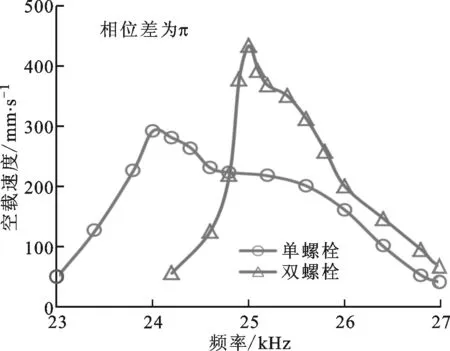
(b)反对称模态图12 样机的空载速度频率特性

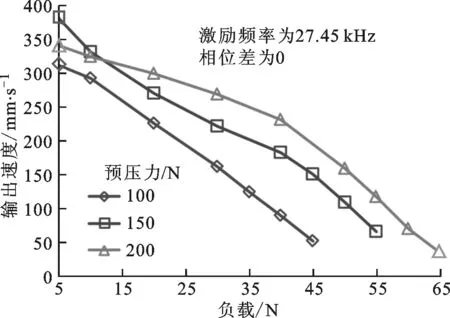
(a)单螺栓样机对称模态

(b)单螺栓样机反对称模态

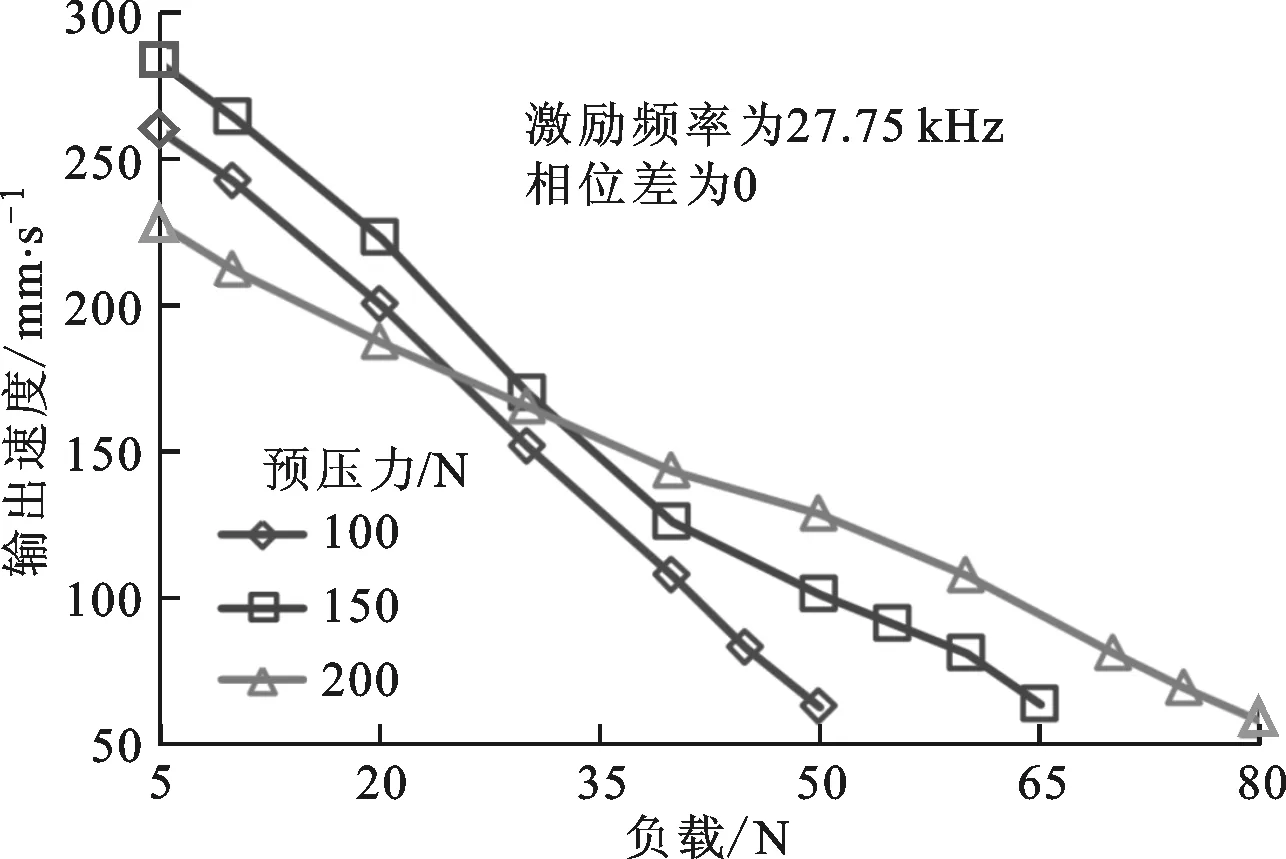
(c)双螺栓样机对称模态

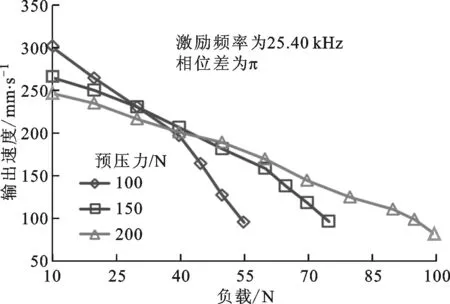
(d)双螺栓样机反对称模态图13 不同样机在不同预压力下的机械输出特性

图13为两样机在激励电压峰峰值为500 V时不同预压力下的机械输出特性曲线,可以看出:电机的输出速度随着负载的增加而近似线性地下降,而且预压力越小,下降趋势越明显。因此,适当增大预压力可提高电机的驱动负载能力。在预压力为200 N、激励电压峰峰值为500 V时,单螺栓样机的对称和反对称模态可分别驱动65 N和90 N的负载,双螺栓样机的对称和反对称模态可分别驱动80 N和100 N的负载。与单螺栓样机比较,采用双螺栓紧固的方式可进一步提高电机的机械输出性能,双螺栓样机对称模态的输出力提高了23.1%,反对称模态的输出力提高了11.1%。电机定子重1.83 N,推重比为54.6。

本文设计的L形直线超声电机与几种现有的直线超声电机的输出性能比较如表1所示。文献[4]和[9]中的电机为V形直线超声电机,文献[11]和[13]中的电机为单模态驱动的矩形板结构直线超声电机。从表1可以看出:V形电机具有较大的输出速度,而板结构电机能获得更大的输出力,但输出U:激励电压;Fmax:最大推力;vmax:最大速度。

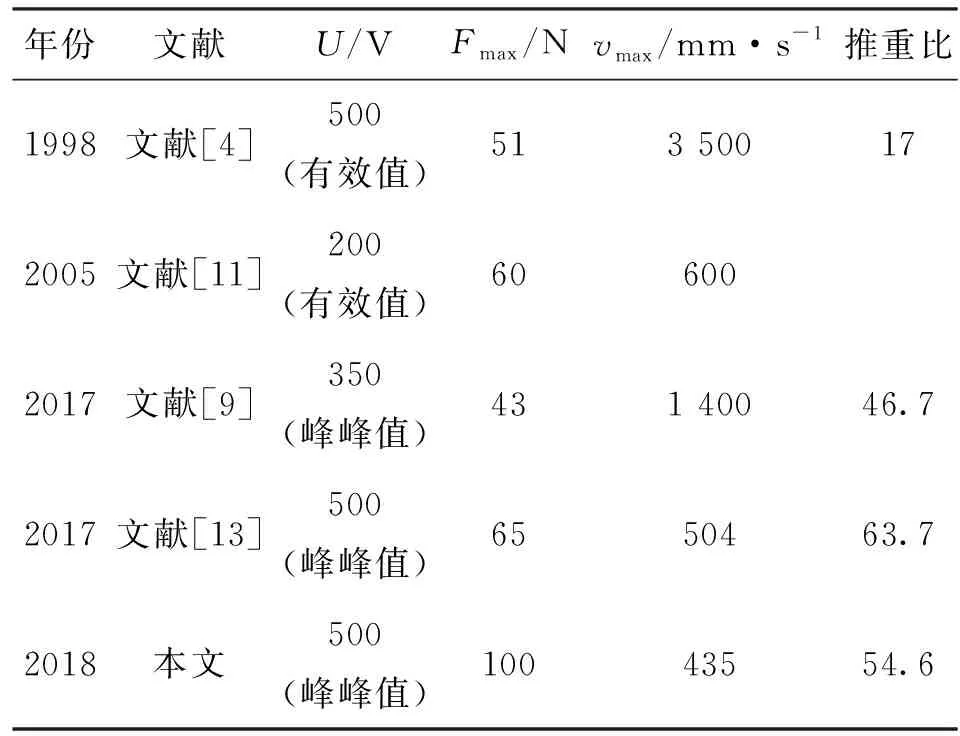
表1 几种直线超声电机的输出性能比较

速度相对较小。这主要是因为二者的工作机理不同,V形电机为模态耦合型电机,而板结构电机为单模态电机。通过对比可以发现,本文研制的L形电机具有较大的推力和推重比,可用于需要大推力且安装空间狭窄的直线驱动场合。

4 总 结

(1)提出了一种单模态驱动的直线超声电机,利用L形板结构定子的对称模态和反对称模态实现了电机的双向运动。

(2)运用有限元方法研究了开槽对驱动足振幅的影响规律。通过在定子前端盖开设一道圆弧形通槽,消除了对称模态在驱动足附近的振动节点,提高了驱动足处的振幅。

(3)利用弹簧模型分析了压电振子中螺栓紧固方式对压电陶瓷预应力的影响,并设计了一种双螺栓紧固方式,即在振子横截面中部两侧中心位置各采用一根预紧螺栓进行紧固,提高了预应力的大小和分布的均匀性。

(4)研制了直线超声电机样机,并测试了其性能。实验表明:采用双螺栓紧固方式可提高电机的机械输出性能;电机在对称模态下的最大速度和输出力分别为405 mm/s和80 N,在反对称模态下的最大速度和输出力分别为435 mm/s和100 N。该电机结构简单、紧凑,运行稳定、推力大,可用于电机安置空间狭窄且需要大推力的直线驱动场合,应具有较好的应用前景。