以数学绘本为媒介 渗透数形结合思想——以“生活中的螺线”一课为例

浙江杭州师范大学附属嘉兴经开实验小学（314000）

纵观整个小学数学，数形结合思想始终贯穿其中:一年级的凑十法、破十法，二年级的有余数除法，四年级的植树问题，六年级的分数应用题……螺线因与圆形有相似性，虽然知识的跨度比较大，但是学生已经在生活中积累了大量的感性认识，因此，六年级的“生活中的螺线”这一课，对于培养学生的数形结合思想是非常有帮助的。

一、以“数”化“形”，借助数列联想图形

“生活中的螺线”这一课所涉及的“数”是数列，对于六年级的学生来说，数列并不陌生，学生已经有过寻找数列的规律，并按规律填数的丰富经验。对于“形”，学生已经掌握了圆的有关知识，虽然从未接触过螺线这个名词，但是在生活中能够找到它的原型。教学时，教师只要引导有效，就能促使学生建立“数”与“形”之间的联系（如图1）。

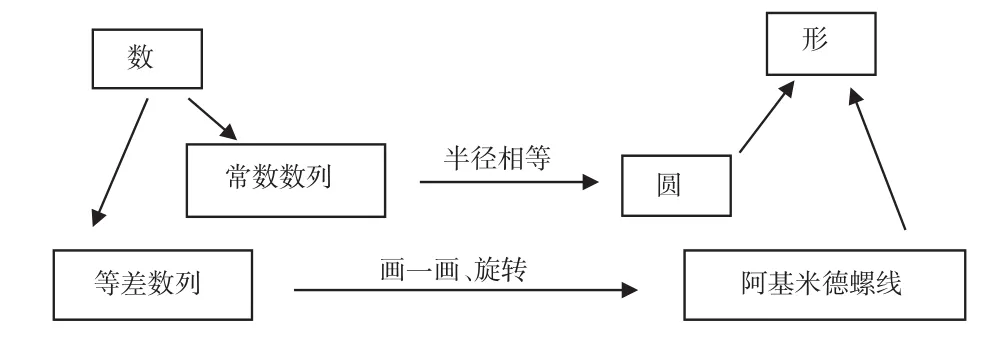
图1

课件出示数列：0 5 5 5 5···

0 1 2 3 4···

师：请比较这两个数列，它们有什么相同点和不同点？

生1：相同点是都有0。

师：对，0通常表示起点，那不同点呢？

生2：第一个数列的每一个数字都是5，第二个数列是1，2，3，4。

师：如果让你猜一猜每个数列后面的数，你认为会是哪些数？

生3：第一个数列后面的数都是5，第二个数列后面的数是5，6，7，8···

师：其实数和形是紧密联系的，看到5 ，5，5，5，你想到了什么图形呢？

生4：正方形。因为正方形每条边都是相等的。

生5：圆。因为圆的半径都是相等的。

师：那么看到1，2，3，4，你会想到什么图形呢？请画一画。

（学生尝试在方格纸上画，得到图2和图3两种情况）

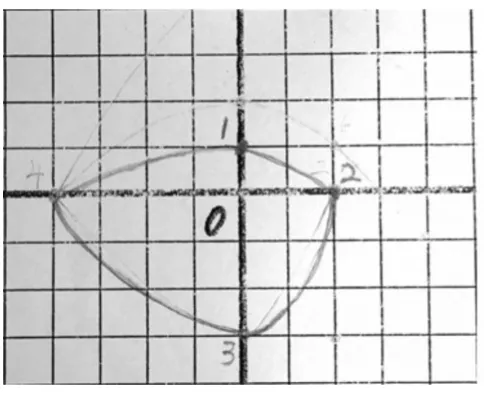
图2

图3

师：刚才我们说4后面应该是5，如果把5也画出来4应该和哪个数相连？5后面是几？还能不能往下画？

生6：4应该和5相连，还可以继续往下画。

师：这个图形的名字叫螺线。螺线和圆有什么类似的地方？有什么不一样的地方？

生7：圆有起点和终点，螺线只有起点，没有终点。

生8：圆上任意一点到圆心的距离都相等，螺线上任意一点到起点的距离不相等。

生9：这条螺线之间的空隙都是相等的。

师：这条螺线被命名为“阿基米德螺线”。因为伟大的数学家阿基米德是第一个研究它的人，所以用他的名字来命名。

通过第一个常数数列中数字都相等的规律，学生结合所学图形的特点，根据四条边相等联想到了正方形，但是由于数列中项的个数是无限的，学生又联想到了有无数条半径、每一条半径的长度都相等的圆。显然，学生不仅从外显上有直观的感受，而且也能够从内涵上将数和形紧密联系起来。转化第二个等差数列对学生来说比较困难，虽然数列不陌生，图案却从来没有接触过，但这是本课的重点，所以这个环节可以先让学生在方格纸上画一画，并在学生反馈时抓住关键问题“4应该是和哪个数连起来？”引发学生的认知冲突，引导学生把数列的特点进一步和螺线联系起来，明确4的后面应该是5，所以4应该和5连接，并可以连续不断地画下去，没有终点。教师通过设置挑战性的任务“看到数列你会想到什么图形呢？”，并以此作为关联点，让学生在观察、想象、操作、探究、修正中经历由数到形转化的具体过程，进一步沟通“数”与“形”之间的联系，从而掌握阿基米德螺线的特征。

二、以“形”变“数”，根据图形研究数列

“形”虽然有形象、直观的优点，但在定量方面还必须借助代数的计算。教师要引导学生充分利用图形的性质或几何意义，把“形”正确表示为“数”的形式后进行分析计算（如图4）。

图4

师(出示图5)：这是鹦鹉螺壳的横截面，这个线条和阿基米德螺线一样吗？用手比画它是怎么旋转的。

图5

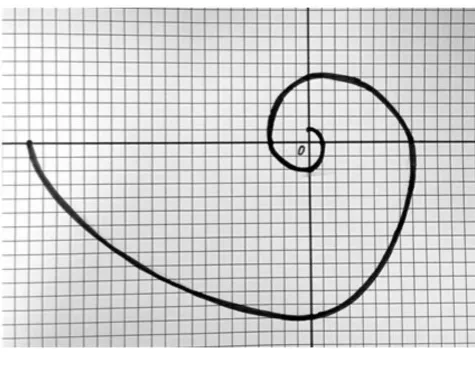
图6

生1：不一样，它旋转不均匀，离起点越来越远。

师：把它也画成螺线会是什么样的呢？（出示图6）它所对应的数列是哪个呢？

生2：看方格图数，得到0，1，1，2，3，5，8，13，21…

师：这个数列有什么特点？

生3：前面两个数相加得到后面那个数。

师：这个数列叫斐波那契数列，用这个数列所画成的螺线叫斐波那契螺线。

在生活中较具代表性的斐波那契螺线的现象是各种软体动物的壳，其中鹦鹉螺是最典型的。教师可出示螺壳横截面，让学生用手比画——想象螺线图——观察得出数列，经历从具体到抽象、从形到数的过程。学生在这个过程中能感受到数学与生活的联系、图形与数列之间的密切关系，感受数学学习的价值。

三、“数”“形”互变，沟通内在联系

解决一些数学问题时，不仅仅是简单的“以数变形”或“以形变数”，而是需要“形”“数”互相变换，不但要想到由“形”的直观变为“数”的严密，还要由“数”的严密联系到“形”的直观（如图7）。

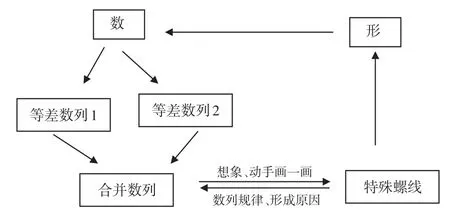
图7

师：如果把数列0，2，4，6，8，10，12…画成螺线，会是哪种螺线？数列2，6，10，14，18…呢？

生1：都是阿基米德螺线，但是螺线之间的距离变宽了。

师：如果我把这两个数列合并在一起呢？画出来会是什么样的？给大家3个选项（如图8）。

图8

生2：选B。

生3：选C。

……

师：为什么没有人选A呢？

生4：两个数列的规律是不一样的，所以合并以后画出来的图形肯定不是匀称的，但不确定是选项B还是C。

师：在方格纸上再画一画吧，看看到底是什么样子。画完后静静地想一想为什么。

生5：选C。画出来就知道了。

生6：选C。因为纵轴的间距小，横轴的间距大。

生7：选C。数列0,2,4,6,8…是画在纵轴上的，相差2；数列2，6，10，14，18…是画在横轴上的，相差4，比纵轴多。因此就形成选项C的螺线。

师：如何能让它形成选项B这样的螺线呢？

生8：两个数列的位置交换一下。

生9：先画横轴，再画纵轴。

……

数形结合思想绝不是简单的由形到数或者由数到形的单向转化，更多情况下是两者互相依存、互相联系、共同存在。在学生学习了阿基米德和斐波那契两种著名的螺线，并感知到了它们的特点后，笔者出示了两个不同的等差数列，让学生先不画图，而是在头脑中想象图像，然后直接判断图像属于哪种螺线，引导学生进一步巩固上一环节所学的知识。最后，笔者设置了挑战性任务“把两个数列合并，合并以后画出来会是怎样一个图形呢？”，促使学生积极参与思考，并且为了能让学生完成学习目标，设计了四个步骤：①独立在头脑中想象；②四人小组讨论并给出选择；③动手画一画；④反馈结果并探究其原因。在整个教学环节中，先由数列想象图形，遇到阻碍再通过画一画跨越障碍，得到正确的螺线图，最后通过螺线图回头分析成因，进一步明晰数列的特征，可谓是数中有形，形中有数，互相转化，密不可分。通过教师有意识、分层次的引导，培养了学生的动手操作能力和分析归纳能力。

总之，数形结合是学生解题的捷径和钥匙，渗透数形结合的思想也是数学基础教学中不可或缺的组成部分，它不仅能培养学生的思维能力，还能提高学生解决问题能力，促进学生数学素养的提升。