韧性水平地震作用下导管架平台非线性时程分析
肖 辉, 关 湃, 朱本瑞, 万 军, 杜夏英, 吴景健, 陈希恰, 庞洪林
(1.中海石油(中国)有限公司 天津分公司, 天津 300459; 2.天津大学 建筑工程学院, 天津 300072)
0 引 言
海洋平台作为海洋油气开发中必不可少的基础设施,暴露在复杂的海洋环境中,长期承受风、浪、流和海冰等环境荷载,同时还可能承受地震等偶然性荷载。地震是一种突发性自然灾害,具有极大的危害性和不可预测性。海洋平台这类大型昂贵的结构在遭遇地震作用时,一旦发生倒塌破坏,将引发巨大的经济损失和环境灾难。因此,海洋石油平台结构的抗震问题受到广泛的关注[1]。
目前,国内在进行导管架平台抗震设计时,大多按照API RP 2A-WSD规范[2]的要求和方法进行,即地震分析校核分为强度水平校核和韧性水平校核。对于强度水平地震采用线性系统的计算方法,通过判断杆件的应力是否达到结构的允许应力来判断结构是否破坏;对于韧性水平地震,推荐使用非线性时程方法进行分析[3]。韧性实际上是结构对外界荷载的承受能力,只要平台不倒塌,就认为平台满足韧性要求,因此不应以应力作为平台失效的判断标准[4-8]。在进行韧性水平抗震设计时,API RP 2A-WSD规范给出了明确的要求[9],即允许平台结构发生一定的破坏,但不能倒塌。
目前,对于导管架平台的抗震性能国内外学者进行了大量的研究。庄一舟等[10]以渤海2座典型导管架平台为研究对象,运用非线性逐步破坏分析方法,得到环境荷载作用下海洋导管架平台结构抗震可靠性的分析方法,并计算了相应的可靠度,通过等效方法简化模拟平台桩-土之间的非线性作用。魏巍[11]对导管架式海洋平台在地震作用下的破坏过程和破坏状态进行了深入研究,将平台破坏过程分为定常、塑变和破坏等3个阶段,并总结了每一阶段的状态特征和分析方法。荣棉水等[12]利用国内外规范地震谱和安评场地地震谱,拟合出具有相同峰值加速度的地震动时程曲线,对简化固定平台模型进行地震动时程分析,结果表明:API规范地震谱偏保守。但文中未考虑材料非线性等非线性特征对于时程分析结果的影响。金书成等[13]基于弹塑性理论,采用push-over方法分析导管架平台的结构响应及平台塑性铰分布等特性,并与时程分析方法结果进行对比。KIMIAEI等[14]证明了导管架平台在极端动荷载作用下的整体响应在很大程度上受到桩基础的非线性影响。以往的研究对于结构的非线性行为考虑得不够全面,并且对于结构在地震作用下的响应分析较为欠缺。本文以渤海某导管架平台为例,基于塑性理论使用USFOS软件进行非线性时程分析,并对结构在强震作用下的响应进行深入的研究。
1 韧性水平地震非线性时程分析
1.1 塑性理论
塑性理论认为材料在达到屈服应力之后仍然能继续受力而不立即发生破坏。USFOS软件中提供2种塑性材料:理想线性-弹性材料和线性-弹性材料。后者考虑了材料的硬化和材料的渐变塑性,因此承载力强于前者,且更符合真实情况。杆件截面完全进入塑性的条件可表示为
(1)
式中:N为轴向力;Q为剪力,分为y、z2个方向;M为弯矩,分为x、y、z3个方向;等式中的分子为杆件截面内力的分量,分母为各个分量的塑性极限。
式(1)可以看成杆件截面内力状态空间中的一个曲面,一旦杆件截面完全进入塑性,其内力状态只能在该曲面上移动,即杆件截面完全进入塑性之后Γ≡0。在分析中,外部荷载按给定的顺序以增量的形式逐步施加到结构上。结构的总刚度矩阵会在每个荷载增量施加时重新合成,并依此计算节点位移的增量。单元内力则根据切线刚度矩阵与单元节点的位移增量计算,并通过迭代的方式使内力与外力相等。然后,判断杆件单元的2个端点和中点位置的截面是否进入塑性以及受压杆件是否发生屈曲。对于进入塑性的杆件单元截面,会在相应位置生成塑性铰,并更新相应杆件单元的刚度矩阵,开始施加下一个荷载增量。根据分析类型不同,在外部荷载施加到给定值或荷载步数达到给定值,或者外部荷载时间历程达到停止时间时结束。
1.2 失效准则
塑性材料的应力超过屈服极限后,若没有失效准则强制杆件失效,材料的应力仍然会继续增大,结构不会发生断裂而是不断被拉长,这显然与实际情况不相符,会导致结构的承载力被高估。因此,需要人为地给结构设置失效准则。地震时程分析通常使用基于应变的失效准则,即当杆件的应变超过某一数值后,后续的分析中此杆件将不再承受任何荷载,此杆件周围的内力也将重新分配。
1.3 动态平衡方程
动态平衡方程是进行时程分析的基础:
FI(t)+Fd(t)+Fr(t)=R(t)
(2)
式中:FI为惯性力;Fd为弹性恢复力;Fr为黏滞阻尼力;R为外力;t为时间。
在时程分析中,力沿着荷载-时间曲线一步一步地施加在结构上,每一步荷载的增量都会导致动态平衡方程的不平衡,通过求解动态平衡方程得出节点力和位移。由于考虑了结构的塑性和大变形,需要在每一步计算结构的刚度、力和位移:
KI(i-1)Δri=ΔRi
(3)
Ri=Ri-1+ΔRi
(4)
ri=ri-1+Δri
(5)
式中:i为时间步;KI为刚度增量矩阵;ΔR为力的增量;Δr为位移的增量。
第i步的力和位移可以通过迭代第i-1步的力和位移的增量得出。刚度增量矩阵是结构现在形态和整个变形时程的函数,所以不能通过迭代的方式得出。在USFOS中,刚度增量矩阵通过欧拉-柯西增量分析法求得,但这种方法会导致计算结果相对于真实解的误差。因此,每步计算后都需要对力进行修正以达到力的平衡,然后通过牛顿迭代法平衡外力和内力。
1.4 结构模拟
本文所使用的分析模型考虑了土壤的非线性行为、土壤性质随土层变化、桩土相互作用的非线性行为、由于辐射和滞后阻尼所导致的能量耗散、材料非线性等诸多因素。结构模型如图1所示,桩-土模型中,在各土层中点位置处生成桩节点,并在各桩节点上根据输入的土壤信息侧向荷载-位移曲线(P-y曲线)、轴向荷载-位移曲线(T-z)曲线、桩端荷载-位移曲线(Q-z曲线),以非线性弹簧的方式施加边界条件。

图1 结构模型
1.5 模态分析
使用图1的结构进行模态分析,前10阶固有周期见表1。其中,第一阶模态为沿y轴振动,第二阶模态为沿x轴振动,第三阶模态为绕z轴振动,如图2所示。

表1 模型固有周期

图2 前三阶模态振型
1.6 地震动时程选择
地震荷载使用地震加速度时程曲线作为输入,由于地震荷载的随机性,API RP 2EQ规范[15]规定使用时程分析方法至少要使用7组地震加速度曲线。计算使用表2所示的7组实测地震加速度曲线[16],将峰值加速度调幅到该平台位置处千年一遇韧性地震加速度水平,将地震激励对土层进行加载。

表2 地震加速度数据

图3 第4组地震作用下平台最大塑性利用率
2 结果分析
2.1 塑性利用率
在通常情况下,通过校核结构的塑性利用率判断在韧性水平地震作用下结构的状态。若材料处于弹性阶段,则塑性利用率为0,代表结构仍可以继续吸收地震所释放的能量;若材料已经完全进入塑性阶段,则塑性利用率为1,说明如果结构继续受力将会产生塑性铰或发生破坏。本文的7组分析结果表明:结构未发生致命性的破坏,整体稳定性良好,不会出现倒塌现象。以第4组分析为例进行说明,分析结果如图3所示。导管架主桩腿结构、桩及组块主立柱结构的塑性利用率较低,几乎仍然处于弹性阶段,这保证了结构整体的稳定性。导管架部分水平撑、X型撑以及组块部分主梁的塑性利用率达到0.3~0.4,但仍然具有吸收能量的能力,而土壤则出现了较为明显的塑性变形,主要出现在浅层土部分。
2.2 平台响应
统计计算结果的最大值,包括基底剪力,垂向反力,上甲板位移、加速度,导管架顶端位移、加速度等参数,见表3,可以看出:平台响应的极值与地震动时程加速度的极值并没有呈现出明显的规律性。以基底剪力为例(如图4所示)进行说明,各组计算得到的最大基底剪力呈现出极大的随机性,并非地震动加速度极值越大平台的响应极值越大。

表3 平台响应最大值

图4 最大基底剪力
图5为第7组地震作用下平台的基底剪力时程曲线与水平向地震加速度时程曲线,最大的基底剪力出现在加速度最大时刻。图6为第4组地震作用下平台的垂向反力时程曲线与垂向地震加速度时程曲线,与基底剪力相同,最大垂向反力出现在地震垂向加速度最大时刻。

图5 第7组地震作用下平台基底剪力与加速度时程曲线
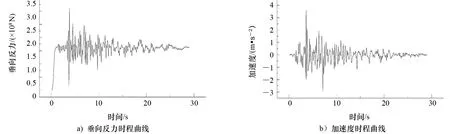
图6 第4组地震作用下平台垂向反力与加速度时程曲线
图7为第5组地震作用下平台上甲板加速度时程曲线(x、y、z向),加速度时程曲线x向和y向表现出类似的运动趋势,而z向加速度的抖动频率更高。平台甲板加速度响应与地震动加速度激励的频谱特征(以x向为例)如图8和图9所示,可以看出:地震动加速度能量在各个频率上分布较为均匀,而上甲板加速度能量主要分布在平台的第一阶自振频率上,这是由于地震动激发了平台的稳态振动。

图7 第5组地震作用下上甲板加速度
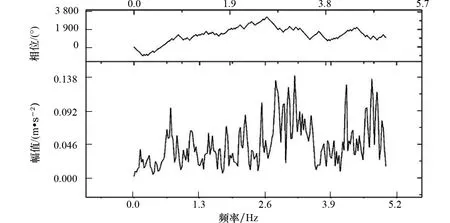
图8 第5组地震动x向加速度频谱特征
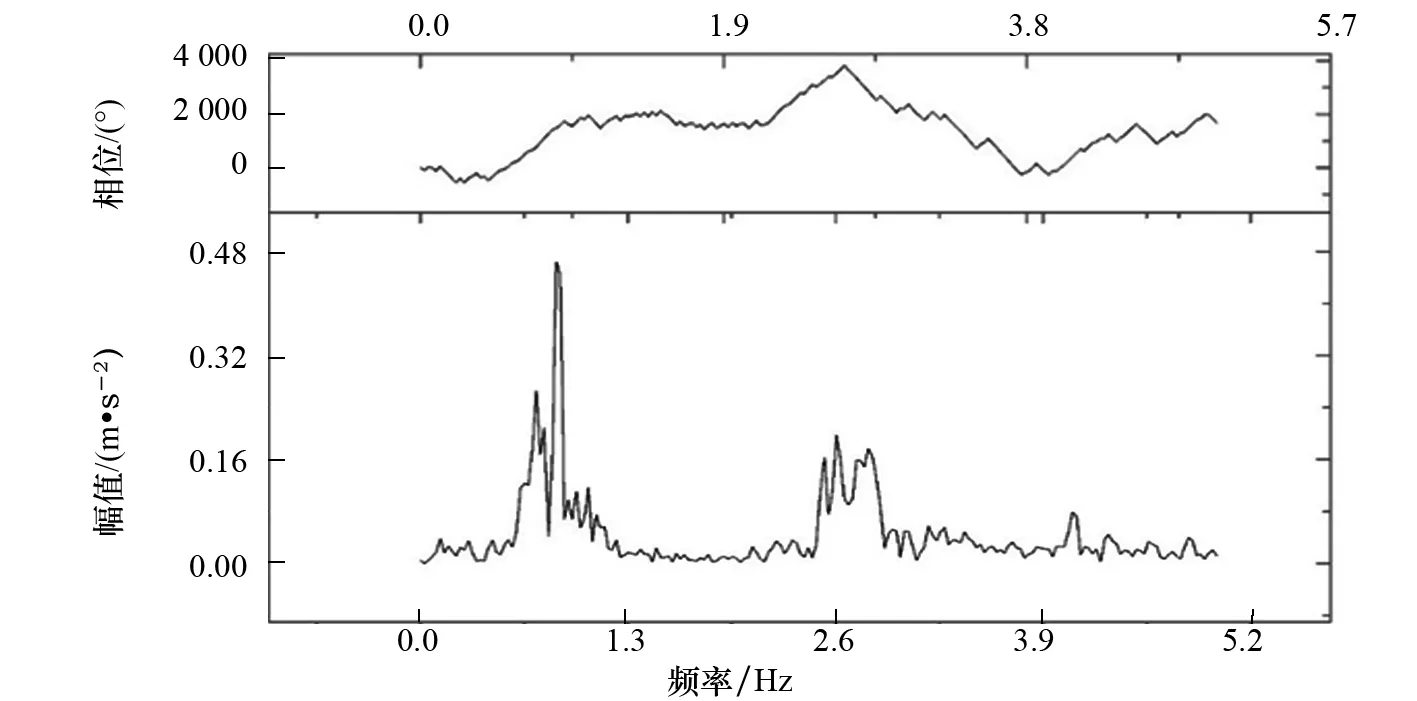
图9 第5组地震作用下上甲板x向加速度频谱特征
3 结 论
(1) 在进行韧性水平地震分析时,如果使用常规的响应谱方法进行设计,则需要大幅度提高构件的规格。但地震荷载是一种惯性荷载,随着杆件尺寸的增加惯性力也随之增大,这在一定程度上是不利的。规范要求考虑结构的塑性承载能力,而非线性时程分析可以考虑材料在屈服极限后的承载能力,此方法更具合理性。
(2) 当结构的塑性利用率处于较低的水平时,结构仍具有一定的承载能力,不会发生倒塌。
(3) 由于地震动时程具有很大的随机性,结构的响应同样具有明显的随机性,但基底剪力和垂向反力的最大值均出现在地震动加速度最大的时刻。
(4) 地震持续时间较短,但影响巨大,可以激发出结构的稳态振动。

