振荡水柱装置前墙形状对能量转化效率影响的数值模拟

郑艳娜， 刘德兴， 陈昌平， 詹 坤， 刘心媚

(1.大连海洋大学 海洋与土木工程学院， 辽宁 大连 116024；2.风力发电系统国家重点实验室， 浙江 杭州 310012)

0 引 言

近年来，伴随着化石能源消耗的不断加剧，世界各国纷纷开始寻找清洁能源。海洋波浪中蕴藏着巨大的能量，据统计，全球可开发的波浪能年储量可达2 TW[1]。研究表明[2]：一年内90%的时间都可进行波浪发电(太阳能和风能约为20%～30%)。自20世纪以来，世界各国的经济重心开始向滨海地区转移，全球有超过一半的人口居住在离海岸线100 km的范围内[3]，从而为波浪能的研究、开发和利用提供良好的现实基础。其中，振荡水柱(Oscillating Water Column，OWC)装置是一种利用波浪能进行发电的装置，是目前进行海洋能开发应用比较广泛的一种形式，对其发电效率的研究一直是各国学者探讨的热点问题。

OWC型装置最早出现在19世纪，作为导航的响哨浮标[4]。随后在1947年，NAGATA等[5]设计和安装了一个OWC发电装置用于航标灯上。在国际能源署的赞助下，从1976年至1979年之间，OWC装置开始安装在浮式结构物上并进行试验。我国对于OWC装置的研究比西方国家发展较晚，截至20世纪80年代中期，我国已经研发成功了10 W型航标灯[6]。如今随着计算机的发展，许多商业软件大量出现，给科学工作者带来了极大的方便。CLÉMENT[7]运用数值波浪水槽研究不同几何参数下OWC波浪转化装置的非线性波浪散射效应。EVANS等[8]运用数值方法研究二维OWC装置前墙入水深度的优化方法。TINDALL等[9]运用数值模拟方法，通过装置前后波浪能量的对比研究OWC装置透平的能量捕获能力。对于三维数值研究，LEE等[10]和BRITO-MELO等[11]运用商业软件对浮式的OWC进行模拟研究。

前墙作为波浪能进出OWC装置的出入通道，对能量的传播和转化的影响十分显著。OWC前墙的结构设计对波浪能的转化效率起着至关重要的作用[7]。EVANS等[8,12]、MA[13]均对OWC前墙的入水深度、腔室尺寸做了研究分析，得到不同前墙入水深度下OWC转换效率与波浪无因次参数Kh的关系，但均未考虑前墙形状的影响。本文基于Fluent软件建立波浪水槽的数值模型，利用建立的数值水槽模型对OWC装置中不同前墙形状的OWC转化效率进行模拟研究，探索前墙形状对OWC转化效率的影响。获得不同前墙形状下，波浪能转化与波浪无因次参数Kh之间的关系，从而为OWC前墙形状的优化提供参考。

1 数值波浪水槽

1.1 数学模型

对于自由面流动问题，流体是不可压缩的，因此，连续方程为

(1)

式中：u为x方向的速度；w为z方向的速度。

动量方程为

(2)

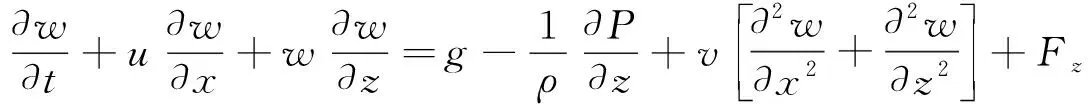
(3)

式中：P为压强；ρ为密度；v为运动黏性系数；Fx为x方向附加的动量源项；Fz为z方向附加的动量源项。

自由表面的运动学边界条件为

(4)

式中：η为自由水面高度；Φ为速度势函数。

自由表面的动力学边界条件为

(5)

水槽的底面和两侧面的边界条件为

(6)

式中：U为速度；k为湍动能；ε为湍动能耗散率；n为壁面的外法线方向。

1.2 数值波浪水槽验证

在研究OWC防波堤的能量转化前，需要对数值波浪水槽进行验证。本文通过对线性波浪的模拟对建立的波浪水槽数值模型进行验证。波周期3.5 s，波高0.8 m，水槽长度为160 m，高度为12 m，水深为4.2 m。采用矩形网格进行划分，并在自由水面附近进行加密。加密网格大小为0.5 m×0.04 m，其他区域取0.5 m×0.1 m。划分好的网格如图1所示。边界类型设置如图2所示。

图1 数值水槽网格的划分 图2 数值波浪水槽边界设置

将数值模拟所得的波形与理论波形进行对比，如图3所示，可以看出：模拟值与理论波形基本吻合，说明数值模拟可以较为准确地模拟线性波浪。

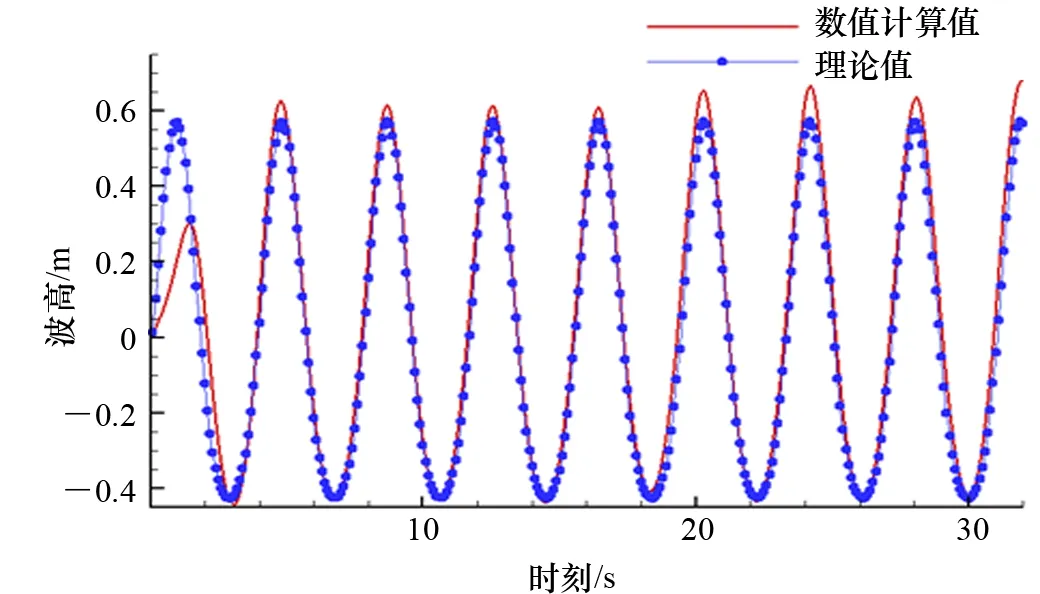
图3 数值模拟波形与理论波形对比

2 OWC数值模型

2.1 数值模型建立

将OWC装置加入数值水槽中，如图4所示。水深h=6 m，前墙入水深度d=2 m。对于OWC结构部分采用三角形网格，网格边长为1 m，水槽部分使用矩形网格，然后进行网格自适应调整，得到OWC整体网格如图5所示。对于边界条件的定义，导气口采用压力入口边界条件，其他边界条件通过加载的造波程序指定。

图4 OWC数值计算域 图5 OWC整体网格

2.2 转化效率计算

EVANS等[8]对OWC转化效率的研究成果表明：在理想流体和线性波浪条件下，前墙和气室是影响能量转化的最主要因素。在不同的条件下，波浪转化效率与他们所对应的波浪无因次参数Kh服从正态分布，即

Kh=khtanh(kh)

(7)

式中：波数k= 2 π /λ，λ为波长；h为水深。

由MICHAEL[14]的研究结论：一个波浪周期内二阶Stokes波浪的入射波浪能量Ei和平均入射波浪功率Pi可分别由式(8)和式(9)计算：

(8)

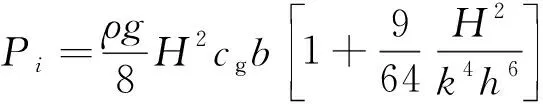
(9)

式中：g为重力加速度；b为OWC装置的宽度；cg为波群速度；H为波高。

基于EVANS、PORTER以及MICHAEL等学者的研究理论，分别对不同波浪条件下的波浪能转化进行CFD仿真计算，采用流体体积函数(Volume Of Fluid，VOF)法追踪波浪自由表面，从微观角度出发对速度场、压力场进行计算。利用Fluent软件自带的监视器对内部两项流进行监测，并提取流速、压力等计算值，用于计算分析Kh与波浪能转化的规律，计算流程如图6所示。

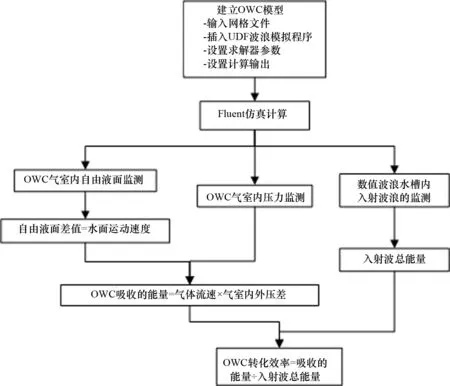
图6 转化效率计算分析流程图

2.3 前墙结构形状

为研究前墙结构形状对OWC波浪能转化装置转化效率的影响，选取5种不同的前墙结构，包括不同的前墙厚度和不同的前墙底端形状，将他们分别命名为案例A、案例B、案例C、案例D、案例E。各组所对应的OWC前墙形状及示意图见表1。

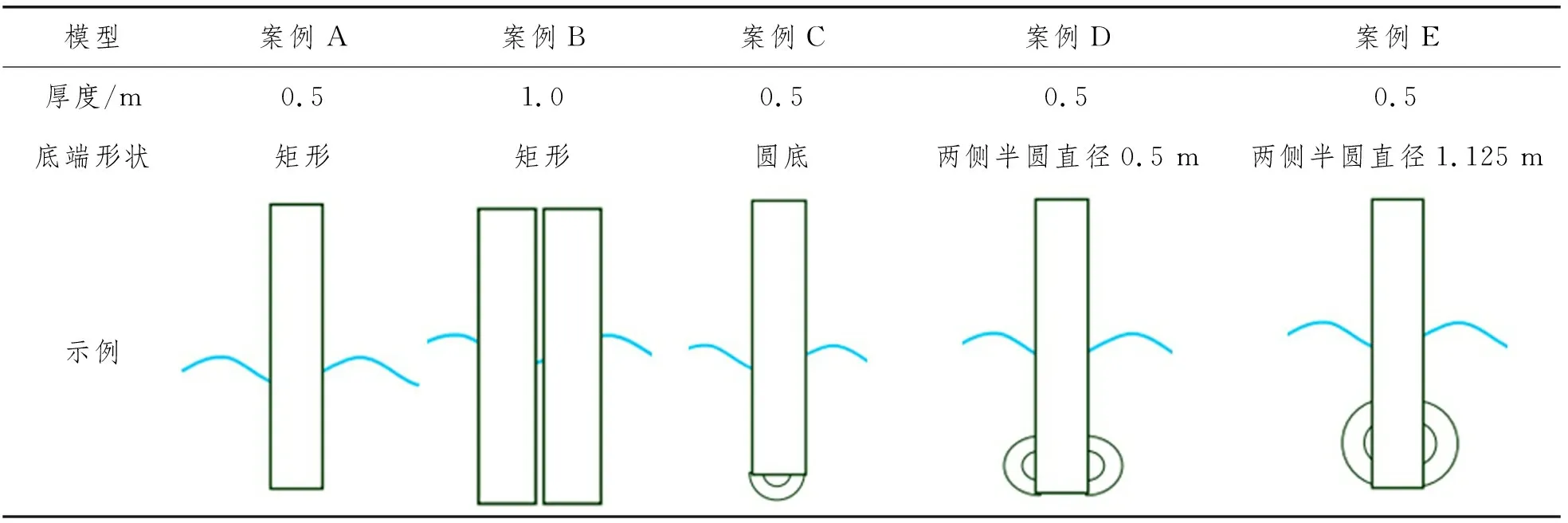
表1 前墙结构形状

3 结果分析

3.1 前墙形状的影响

3.1.1 计算波况

为得到Kh与OWC转化效率的关系，分别对每种前墙形状在不同波浪条件(不同Kh值)下的转化效率进行计算，计算波况见表2。计算继续采用二阶Stokes波浪，波高H=2 m，水深h=6 m。

表2 计算波况

3.1.2 转化效率

不同前墙形状条件下，计算得到Kh与转化效率的关系曲线如图7所示。为更加清晰地了解各前墙形状对转化效率的影响，制作B、C、D、E各案例相对于案例A(对照组)的相对转化效率，如图8所示。

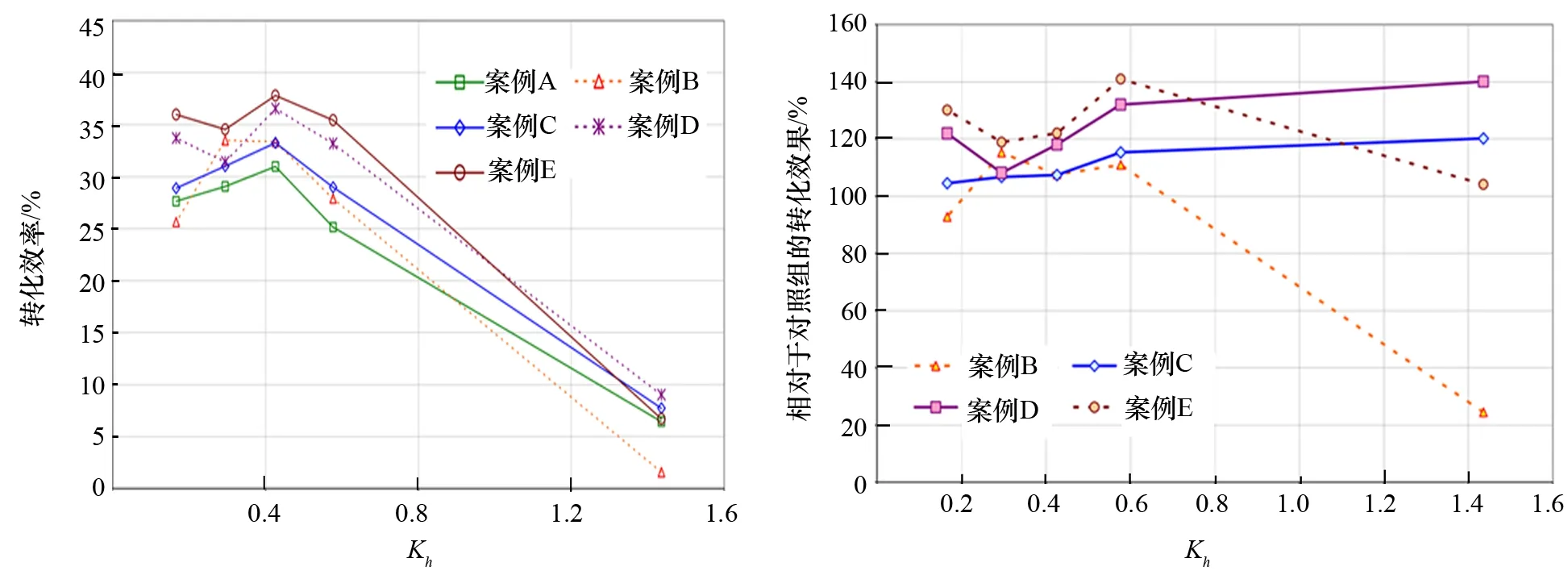
图7 不同前墙形状下的转化效率 图8 不同前墙形状下的相对转化效率

从图8可以看出：相对于对照组(案例A)，案例B(矩形，2倍前墙厚度)所对应的转化效率在一定Kh值范围内有所提升，在Kh值较大或者较小的情况下均会导致转化效率降低。案例C、案例D、案例E在Kh值全范围段内转化效率均有提升。这说明，在前墙底部和两侧进行光滑设置都能较好地提升转化效率。为更好地分析各案例之间的转化效率情况，将各案例组转化效率的平均值进行对比，结果见表3。

表3 各组转化效率 %

由表3可以看出：转化效率平均值案例E>案例D>案例C>案例B。这说明单独增加前墙厚度(案例B)，不改变形状，对转化效率影响不大；与底部增加半圆形状(案例C)相比，在OWC前墙两侧增加半圆(案例D、案例E)对能量转化具有明显的提升效果。比较案例D和案例E的结果可以发现，将两侧半圆的直径由0.5 m增加到1.125 m也可以增加能量转化效率，但提升效果有限。

3.2 优化后的转化效率

3.2.1 计算波况

通过3.1节的计算可知：案例E的结构形式能量转化率较高。因此增加计算波况，对优化后的案例E和原型的案例A等2种形式的转化效率进行对比研究。计算波况见表4。

表4 计算波况

3.2.2 转化效率对比

图9为基本模型案例A和后处理模型案例E等2种前墙形状，在多种波况条件下的转化效率对比图，可以看出：两者的转化效率随Kh的变化曲线相似，在Kh=1.5附近转化效率达到最大值，案例E的转化效率普遍高于案例A，最大转化效率达90%以上。经计算，案例E模型相对案例A模型的计算结果平均增长率约为18%，说明前墙两侧增加半圆的处理方式能很好地提升OWC的转化效率。

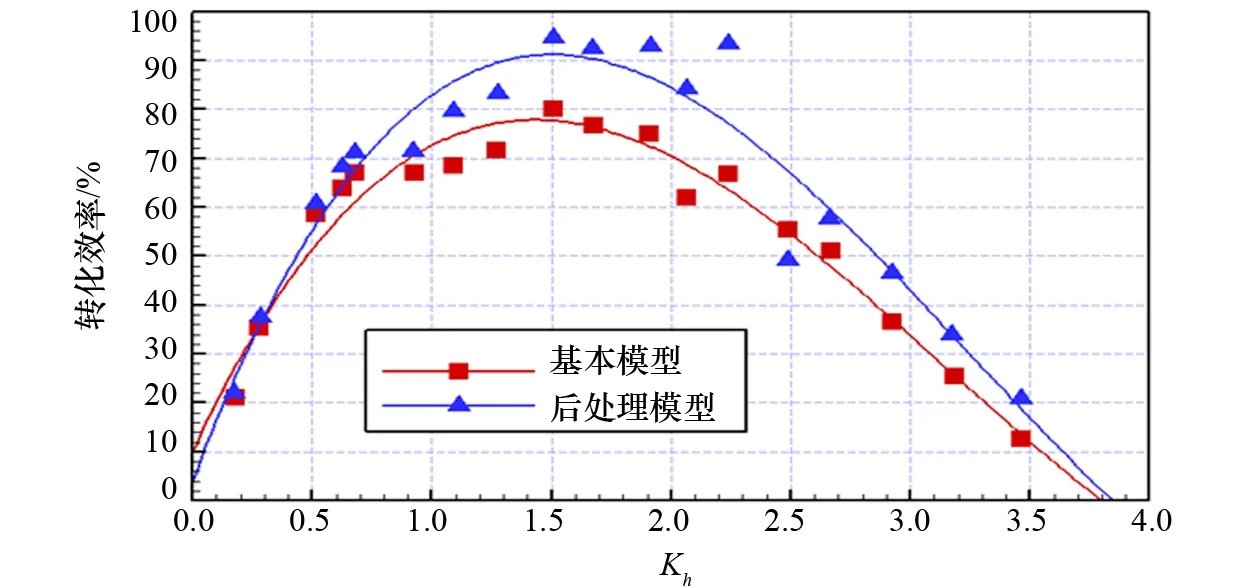
图9 案例A与案例E转化效率对比

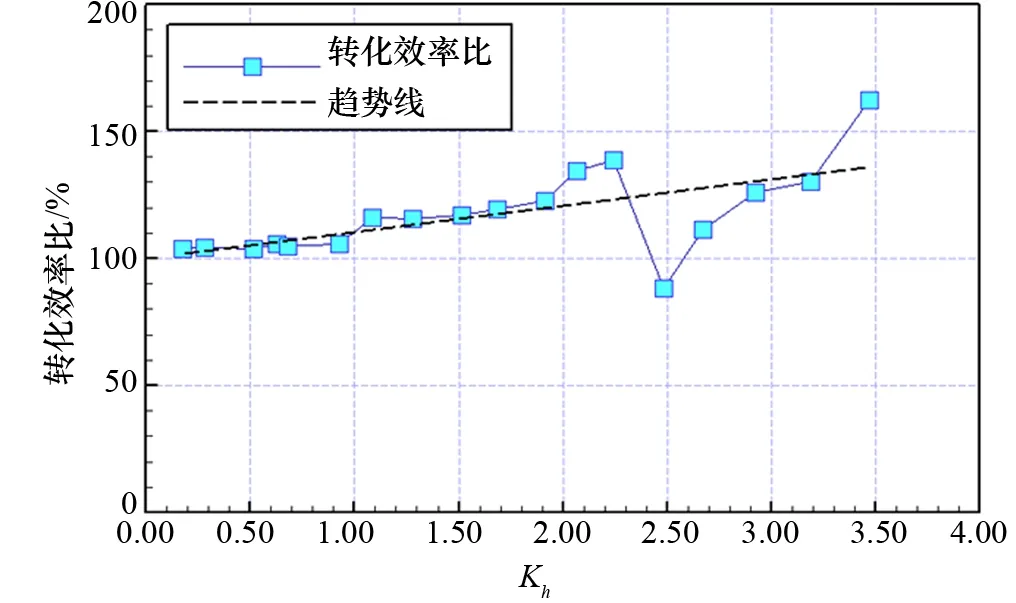
图10 转化效率比曲线图

为了便于对比分析，取转化效率比=案例E转化效率/案例A转化效率，将其作为纵坐标，横坐标仍为波浪无因次参数Kh，如图10所示，可以看出：转化效率比值随着Kh值的增加呈增长趋势，这主要是因为随着Kh值的增加，流体流速增加，而流速的增加使矩形前墙周围更容易生成涡流从而造成能量损失。因此，在Kh较大的情况下，对前墙两侧增加半圆处理后，能量转化效率提升更为明显。

4 结 论

(1) 基于Fluent软件的数值波浪水槽能够较为准确地模拟线性波浪。

(2) 单独增加OWC装置的前墙厚度，不改变形状，对转化效率影响不大；前墙底端两侧增加半圆可有效地提升转化效率，增大半圆的直径对转化效率的提高作用有限；经前墙优化后的结构最大转化效率可达90%以上，平均能量转化效率的提升达18%。

(3) 在波浪无因次参数Kh较大的情况下，对前墙两侧增加半圆处理后，能量转化效率提升更为明显。